Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Lagrangian Mechanics

111

density of the bar; this force derives from the simple potential

′

−+

(/2)( sin)dkxμρ θ . Noting that

===

∫∫∫

d,d0, d

BBB

AAA

xM xx xxIμμμ,

we get

()

′′

=− + =− +

∫

sin d sin

UxxMIρθμ ρ θ

(18.3.64')

One obtains, easily,

′

==− =−

12 23

0, , sin 2

QQkMQ Iρθ

(18.3.64'')

We are thus led to Lagrange’s equations

′′′

==− =−

12 2

0, , 2 sin 2kkρρ ρθ θ



 

(18.3.65)

The mass centre

C describes a sinusoid along the

′′

Ox -axis, its projection on this axis

having a uniform motion; the bar oscillates about the

′′

Ox -axis with a frequency equal

(in case of small oscillations with

≅sin θθ, hence ≅sin 2 2θθ) to the frequency of

the oscillations of the projection of the centre

C on the

′′

Ox -axis.

18.3.2.8 Double Pendulum

We return to the double pendulum, considered in Sect. 17.1.1.2. This mechanical

system has two degrees of freedom and we can choose as generalized co-ordinates the

angles made by

and

, respectively, with the descendent vertical

(

1122

,qqθθ

); we have denoted by

the suspension pole of the solid

S with the

mass centre

and by

the hinge between this solid and the solid

S , with the mass

centre

(see Fig. 17.1, a too). The kinetic energy of the mechanical system

≡

{, }SSS is given by

{

}

⎡⎤⎡⎤

′′′

=+ + +

⎣⎦⎣⎦

(2) (2)

11 2 22

11 1

22 2

TI M I

θρρ θ



(18.3.66)

where

is the moment of inertia of the rigid solid

S with respect to the

′′

Ox -axis,

while

is the moment of inertia of the rigid solid

S , of mass

, with respect to

the axis which passes through the centre

of co-ordinates

′′

(2) (2)

,ρρ and is parallel

to the axis

′′

Ox . We notice that

′′

=+ =+

(2) (2)

12 2 12 2

cos cos , sin sinll llρθθρθθ;

we obtain thus

MECHANICAL SYSTEMS, CLASSICAL MODELS

112

()()

′

=+ ++ + −

22 22

121 2222 2212 21

cos( )

TIMl IMl Mll

θθθθθθ



(18.3.66')

As well, the potential of the weight forces is

()

=+ +

11 1 2 1 2 2

cos cos cosUMgl Mgl lθθθ.

(18.3.67)

Lagrange’s equations read

()

() ()

()

() ()

++ −−−

⎡

⎤

⎣

⎦

=− +

++ −+−

⎡

⎤

⎣

⎦

=−

12122 212 212

11 2 1

222222 211 211

22 2

cos sin

sin ,

cos sin

sin .

IMl Mll

Ml Ml g

IMl Mll

Mlg

θθθθθθθ

  

(18.3.68)

We find thus again (17.1.4), which have been studied and integrated by Bradistilov and

by Anca Zlătescu. The small oscillations of the double pendulum have been considered

in Sect. 17.1.1.2.

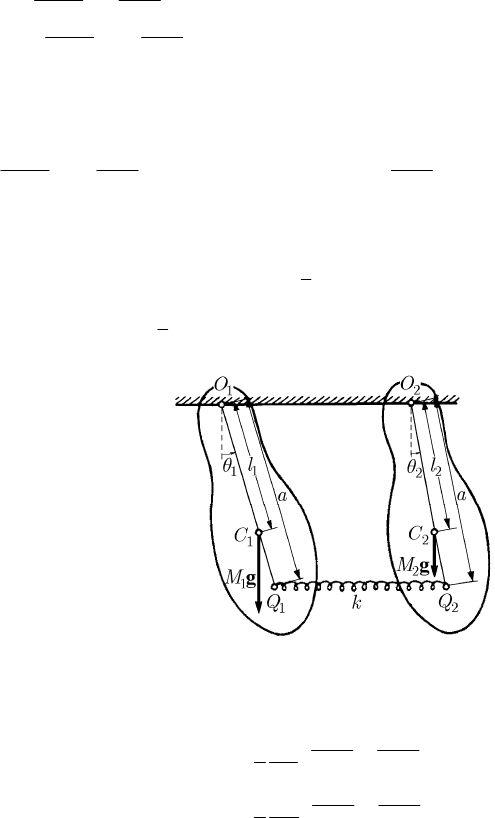
18.3.2.9 Sympathetic Pendulums

The sympathetic pendulum has been considered directly with the aid of Newton’s

equations in Sect. 17.1.1.3. We take again the problem in case of the two physical

pendulums of masses

M and

M , the gravity forces being applied at the mass centres

C and

C , respectively; we denote ==

11 1 22 2

,OC l OC l , where

O and

O are the

poles through which pass the axes of suspension. The two pendulums are connected by

an elastic spring

QQ , so that the point

Q is on the straight line

OC , while the point

Q is on the straight line

OC , with ==

11 22

OQ OQ a (Fig. 18.13). The spring

QQ is characterized by the elastic constant k , so that the magnitude of the force

which arises in the spring is given by

−

12 12

||kOO QQ

, where = constk (unlike the

case considered in Sect. 17.1.1.3, where the elastic constant depends on the mass of the

physical pendulum upon which acts the spring, the position of the points

Q and

playing no one rôle).

The position of this mechanical system is specified by the generalized co-ordinates

and==

11 22

qqθθ, these ones being the angles made by

OC and

OC ,

respectively, with the vertical line. The kinetic energy is given by

()

11 22

TIIθθ



(18.3.69)

where

I and

I are the moments of inertia of each pendulum with respect to the

corresponding axis of suspension. The potential

is expressed in the form

()

=+−−

11 1 22 2 1 2 1 2

(cos cos)

UgMl Ml OOQQθθ .

Lagrangian Mechanics

113

But

()

[

]

() ()

[]

=+ − + −

=+ −+− −

12 12 2 1 2 1

sin sin (cos cos )

2sinsin21cos .

QQ OO a a

OO aOO a

θθ θθ

In the case of small oscillations, we have

≅

sin θθ

≅

sin θθ

, ≅−

cos 1 /2θθ,

≅−

cos 1 /2θθ, so that

()() ()

[

]

+−+−=+−

12 12 2 1 2 1 12 2 1

2QQ aOO a OO aθθ θθ θθ .

Hence, in case of small oscillations, it results

()

=+− +

−++

11 22 1 1 1

22 2

22 2 12

UgMl Ml Mgl ka

Mgl ka ka

θθθ

(18.3.69')

Fig. 18.13 Sympathetic pendulums

Lagrange’s equations read (

=+TUL )

()

∂

++−=

∂

++−=

∂

11 1 1 1 1 2 1 2

22 2 2 2 1 2 1 2

sin 0,

sin 0 .

I M gl OO QQ

IMgl OOQQ

θθ



(18.3.70)

In case of small oscillations, we get

()

++−=

11 1 11 1 2

22 2 22 1 2

IMglka

I M gl ka

θθθθ



(18.3.70')

In the particular case of two identical physical pendulums (

MMM

lll, ==

III), we may write

MECHANICAL SYSTEMS, CLASSICAL MODELS

114

()() ()()

∂∂

++ += −+ −=

∂∂

12 12 12 12

0, 0

θθ ωθθ θθ ωθθ

where we have introduced the pulsations (

′

is the length of the synchronous

mechanical pendulum)

()

== = + =+

′

22 22

Mgl g ka

Mgl ka

Il I

ωω ω.

(18.3.71)

Hence, we obtain

() ()

[]

() ()

=+ +−

⎡⎤

++ +−

⎢⎥

⎣⎦

00 00

112 12

00 00

12 12

() cos cos

11 1

sin sin .

ttt

θθθωθθω

θθ ω θθ ω

ωω

 

(18.3.72)

() ()

[]

() ()

=+ −−

⎡⎤

−+ −−

⎢⎥

⎣⎦

00 00

212 12

00 00

12 12

() cos cos

11 1

sin sin ,

ttt

θθθωθθω

θθ ω θθ ω

ωω

 

where

(0)

θθ



, ==

(0), 1,2

kθθ , corresponding to the initial moment = 0t .

If ====

0000

1212

,0, 0θθθ θθ



, then we get

()

−+

=+=

−+

=−=

000

( ) cos cos cos cos ,

222

() cos cos sin sin ,

222

ttt

θωωωω

θωωθ

θωωωω

θωωθ

(18.3.72')

These results correspond to those in Sect. 17.1.1.3, excepting to the different

definition of the elastic constant

Chapter 19

Hamiltonian Mechanics

The motion of the representative point

∈

P Λ is governed by a system of s differential

equations of second order (Lagrange’s equations) in Lagrangian mechanics. In 1834,

W. R. Hamilton had the idea to use a representative space with

2s dimensions, the motion

of a representative point in this space being specified by a system of

2s linear differential

equations (Hamilton’s equations); The new formulation (in the frame of Hamiltonian

mechanics) is equivalent to the Lagrangian formulation for discrete mechanical systems

with holonomic, ideal constraints, being put a restrictive condition: these systems must be

natural (as a matter of fact, the considered systems must admit a Lagrangian). These

equations have remarkable analytical properties, leading to a rigorous and elegant

mathematical formulation of the quantic model of mechanics. Especially, the Hamilton–

Jacobi partial differential equation allows to pass from the matric quantum mechanics to the

undulatory mechanics.

In this order of ideas, after a study of Hamilton’s equations, we will consider in detail the

Hamilton–Jacobi method (Arnold, V.I., 1976; Dobronravov, V.V., 1976; Goldstein, H.,

1956; Lurie, A.I., 2002; Routh, E.J., 1892, 1898; Ter Haar, D., 1964).

19.1 Hamilton’s Equations

After establishing some results with a general character, including Hamilton’s equations,

we make a study of several expressions which play a special rôle: Lagrange’s brackets and

Poisson’s brackets; these results will be illustrated by some applications to particular

mechanical systems.

19.1.1 General Results

To pass from the space of configurations to the phase space, one introduces the canonical

co-ordinates and one obtains Hamilton’s canonical equations; after putting in evidence

some properties of the latter ones, one considers Routh’s equations, as well as other

equivalent equations.

19.1.1.1 Canonical Co-ordinates. Phase Space. Associate Expressions

To study a natural discrete mechanical system

S of n particles, subjected to

holonomic ideal constraints, we consider Lagrange’s equations (18.2.38) (where we have

introduced the kinetic potential

=+TUL ), which describe the motion of the

representative point

( , ,..., )

Pq q q in the space of considerations

. To pass from this

115

P.P. Teodorescu, Mechanical Systems, Classical Models,

MECHANICAL SYSTEMS, CLASSICAL MODELS

116

system of equations of second order to a system of equations of first order, one has an

infinity of possibilities to proceed (e.g., as in Sect. 18.2.3.8).

Thus, in Sect. 18.2.3.6 there have been introduced the generalized momenta by means of

relations (18.2.80). Taking into account (18.2.81) and (18.2.15), (18.2.15'), and (18.2.15''),

we can write

=++=, 1,2,...,

jjj

jk k

pgqgUj s .

(19.1.1)

Introducing the normalized algebraic complement

g of the element

g of the deter-

minant

=≠det[ ] 0

, which verify the relations (18.2.44), we obtain, easily,

=− + =( ), 1,2,...,

kjk

kkk

qgpggUj s .

(19.1.1')

Let

′

Λ be the space of the points

12 12

( , ,..., , , ,..., )

Pq q q q q q ; let us introduce also the

representative space

Γ of the representative points

12 1 2

( , ,..., , , ,..., )

Pq q q p p p . We

notice that the formulae (19.1.1), (19.1.1') establish a one-to-one correspondence between

the two spaces. A state of the considered discrete system

S is represented, as we have

shown in the preceding chapter, by a representative point in the space

Λ , hence by a point

in the space

′

Λ , and this one is represented, in a one-to-one mode, by a representative

point in the space

Γ . The representative space

Γ is called the phase space (or the

Gibbs’s space).

The co-ordinates

12 1 2

, ,..., , , ,...,

qq qpp p of the corresponding representative point

P (the set of generalized co-ordinates and the set of generalized momenta) are called

canonical co-ordinates (Hamiltonian co-ordinates); the generalized momenta

p are co-

ordinates conjugate to the generalized co-ordinates

q . We replace thus the study of the

motion of the mechanical system

S in

E by the study of the motion of the representative

point

P in the space

Γ . Having to do only with holonomic constraints, which are

eliminated by passing to generalized co-ordinates, the representative point

∈

P Γ is a

free point.

To study the motion of the point

P , we will express the quantities of energetical nature

used in the space

Λ by means of the canonical co-ordinates in the space

Γ ; by passing

to canonical co-ordinates, a function

(,;)

Fq q t

becomes a new function (, ;)

Fq p t



called the associate expression of the function

F , so that

=(,;) (, ;)

jj j j

Fq q t Fq p t





. The

quantities (18.2.15'), (18.2.15'') read

=−++++

=− +

11 1

() ()(),

22 2

(),

jk jk jk

jjjj jj

jk k k k k k

jk jk

jj j j

kkk

gqq gpp gg Up gg Ug U

gq g gp g g g U





where we took into account the relations (18.2.44). The kinetic energy will take the

form

Hamiltonian Mechanics

117

=++

TT TT



(19.1.2)

where we have put in evidence a quadratic form, a linear form and a constant with

respect to the generalized momenta, given by (we notice that

≠=,0,1,2

TTk



)

==−=−−+

,,()

jk jk jk

jj jj

kk kk

TgppTgUpT gggUUg.

(19.1.2')

We get thus the associate expression of the kinetic energy by means of the canonical co-

ordinates. If the generalized forces derive from a simple quasi-potential, then we have

==0, 1,2,...,

Uj s, so that =

0T ; as well, if the mechanical system is scleronomic,

then it results

==0, 1,2,...,

gj s, and =

0g , so that

(1/2)

TgUU

. If both

conditions are fulfilled (the mechanical system is scleronomic and the generalized forces

derive from a simple quasi-potential), then we obtain

0TT , so that =



. In

this case, the relations (19.1.1) read

pgq ,

(19.1.1'')

the generalized momenta vanishing together with the generalized velocities. This

property does no more take place if the mentioned conditions are not fulfilled.

After a partial differentiation of (18.2.15) with respect to

q , we multiply by

q and

sum for all the values of the index

; it results

∂∂

∂

=++=+

∂∂∂∂

210

jjjj

qqqq TT

qqqq



where we used Euler’s theorem concerning the homogeneous functions. Adding

2TT to both members of this relation and using the relation (18.2.81) and the

notations (18.2.15''), (18.2.15'''), we may write

=+−+

()

jj j j j

Tqp gUqg,

(19.1.3)

obtaining thus a new remarkable expression for the kinetic energy.

By an analogous calculation, the associate expression of the generalized quasi-

potential (18.2.22) will be of the form

=+ = =− + +

00 0

,, ()

kjk

kkk

UU UU gpU gUg U U



(19.1.4)

hence a sum of a linear form and a constant with respect to the generalized momenta. In

case of a simple quasi-potential (

= 0

U ), we have ==

UU U



Observing that

0TU , the associate expression of the kinetic potential

(18.2.34) is given by

MECHANICAL SYSTEMS, CLASSICAL MODELS

118

=+ = =− + + ++

00 00

222

,, ()()

TggUgUgU



LLLL L

(19.1.5)

hence it will be a sum a quadratic form and a constant with respect to the generalized

momenta. In case of a scleronomic mechanical system and of forces which derive from

a simple quasi-potential we have

UL , while

L is a positive definite form in the

generalized momenta.

We notice that one can make the transformation (18.2.80) in case of a non-natural

mechanical system too, if the condition (18.2.34''') is fulfilled. Indeed, in this case the

Jacobian of the functions

∂∂

qL is the Hessian of the kinetic potential; thus, the

theorem of implicit functions allows to calculate

12 1 2

( , ,..., , , ,..., ; )

qqqq qpp pt ,

= 1,2,...,

. Obviously, these relations are linear with respect to the generalized

momenta, so that the most important results previously obtained remain valid.

19.1.1.2 Donkin’s Theorem. Legendre’s Transformation

Let be a function

( , ,..., )

XXxx x of class

, for which the Hessian is

non-zero

∂

⎡⎤

≠

⎢⎥

∂∂

⎣⎦

det 0

(19.1.6)

Let us consider a transformation of variables generated by the function

X in the form

∂

, 1,2,...,

yjs

(19.1.7)

We can state

Theorem 19.1.1 (Donkin). A transformation (19.1.7) for which the condition (19.1.6) is

fulfilled being given, there exists a transformation, inverse to this one, generated by a

function

( , ,..., )

YYyy y of class

C , by means of the relations

∂

,1,2,...,

xjs

(19.1.7')

The two functions are linked by the relation (we assume that the variables

x are

expressed with the aid of the variables

y ; as well, the function Y too)

XY xy.

(19.1.8)

12 1 2

( , ,..., ; , ,..., )

XXxx xαα α , where =, 1,2,...,

kmα , are given parame-

ters, then we have

12 1 2

( , ,..., ; , ,..., )

YYyy yαα α too, so that

Hamiltonian Mechanics

119

∂∂

=− =

∂∂

, 1,2,...,

αα

(19.1.9)

Indeed, the Hessian of the function

X coincides with the Jacobian of the functions

in the second member of the relations (19.1.7); on the basis of the condition (19.1.6),

the theorem of implicit functions shows that, using the mentioned relations, we can

obtain

( , ,..., ), 1,2,...,

xxyy yj s. Calculating the function Y from the

relation (19.1.8) and expressing it by means of the variables

=, 1,2,...,

yj s, we

obtain

()

∂∂

∂∂ ∂

=−=+−

∂∂ ∂ ∂∂

kk k

jjj

xy X y x

yy y xy

Taking into account the relations (19.1.7), we get the relations (19.2.7'), which are

thus justified. If in the function

X intervene also the parameters

α , 1,2,...,jm= ,

then these ones intervene in the direct transformation (19.1.7) too; hence, we have

to do with

12 1 2

( , ,..., ; , ,..., )

xxyy yαα α= , 1,2,...,

s= , as well as with

12 1 2

( , ,..., ; , ,..., )

YYyy yαα α . We can calculate

()

∂∂

∂∂ ∂ ∂ ∂

=−=−−=−

∂∂ ∂ ∂∂∂ ∂

kk k

jjjjj

YXXX

xy X y

αα α αα α

where we took into account (19.1.7). The theorem stated by Donkin in 1854 is thus

completely proved.

The passing from the variables

to the variables

, considered above, is known

as Legendre’s transformation.

For instance, in the mathematical modelling of thermodynamics, where

=XH is

the enthalpy,

−=YG is Gibbs’s function of state, = 1s , =

xS is the entropy,

while

yT is the absolute temperature, takes place the relation

−=HG ST, (19.1.10)

the product

ST being the bound energy; the relations

∂∂

==−

∂∂

(19.1.10')

take place.

19.1.1.3 Canonical Equations

We will use Donkin’s theorem and Legendre’s transformation to establish the

equations of motion of the representative point

∈

P Γ . We take thus =X L ,

xq , =

yp, ==, 1,2,...,

qj sα , as well as =

tα , =+1ms ; because of

MECHANICAL SYSTEMS, CLASSICAL MODELS

120

the condition (18.2.34'''), the condition (19.1.6) is fulfilled. We introduce the function

=YH, called Hamilton’s function (Hamiltonian), in the form

=−

Hpq L

(19.1.11)

=−

Hpq







L , then it results =

12 1 2

( , ,..., , , ,..., ; )

HHqq qpp pt. We may

write

∂∂



(19.1.12)

∂∂∂∂

=− =

∂∂∂∂

qqtt

(19.1.12')

for

= 1,2,...,

s . If in Lagrange’s equations (18.2.38) we take into account the first

relations (19.1.12), then we can replace these relations by the equivalent system

∂∂

==−

∂∂



(19.1.13)

Using the first relations (19.1.12') and associating the last relations (19.1.12), there

result the equations of motion (given by Hamilton in 1834) of the representative point

in the space

in the normal form

∂∂

==−=

∂∂

, , 1,2,...,

qp js



(19.1.14)

These equations are the canonical equations of Hamiltonian mechanics (Hamilton’s

equations) (Hamilton, W.R., 1890).

Using the relation of definition (19.1.11), we get

∂

∂∂∂

⎛⎞

=− + − + −

⎜⎟

∂∂∂∂

⎝⎠

∂

∂∂

⎛⎞

=+ −

⎜⎟

∂∂∂

⎝⎠

jjj

pp p

pqqq

pqp













If the system (19.1.13) is verified, then one obtains Hamilton’s equations. On the other

hand, if the canonical equations are verified, then the second relations obtained above

lead to the first equations (19.1.13); indeed, one obtains a homogeneous system of

linear algebraic equations for which the determinant of the coefficients

∂∂det[ / ]





is the inverse of the determinant

∂∂det[ / ]



 , which is thus the Hessian (18,2,34'''),

hence being non-zero (if

=+TUL , then this determinant is equal to 1/g ). Then,

the first above relations lead to the last equations (19.1.13). We can thus state that

Hamilton’s equations are equivalent to the equations (19.1.13), which – at their turn –

are equivalent to Lagrange’s equations.