Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Variational Principles. Canonical Transformations

241

where

()

, ,...,

uuqq q= is a given positive function of class

C ; we may consider

θ as an artificial time, measured in the motion of the representative point in the space

as in Sects. 19.2.2.1, 19.2.2.3, and 19.2.2.3.

Denoting by

()

12 12

, ,..., , , ,...,

qq qqq q

′′ ′

′′

LL , d/d

qqθ

′

= , 1,2,...,js= ,

the new form of the function

L by introducing the new generalized velocities, we can

write the principle (20.1.47) in the form

ΔΛθ=

∫

()

uhΛ =+

′

L .

(20.1.47')

The corresponding Euler–Lagrange equations

ΛΛ

∂∂

⎛⎞

−=

⎜⎟

∂∂

⎝⎠



, 1,2,...,

s= ,

(20.1.49)

hold only for generalized conservative mechanical systems (

d/d 0θ==

′′



LL and

h=E ); one obtains thus the trajectory of the representative point in the phase space,

but not the direct connection between the position of the point on the orbit and the time.

If we denote by “prime” the change of independent variable in a certain quantity, we

can write

222

/TTTuθ

′′



111

/TTTuθ

′′



, so that

()()

210 1 0

uT T T U h T uT U h

′

=++++=++++

;

(20.1.50)

the corresponding first integral of Jacobi type leads to the condition

()

TU h

′

−+=

(20.1.50')

In particular, let be a mechanical system with two degrees of freedom for which

()

21111212222

Tgqgqqgq=++



11122

Tgqgq=+;

(20.1.51)

by a convenient transformation we can pass to isothermic (isometric) co-ordinates for

which (by convention, we can use the same notation for the generalized co-ordinates)

()

212

Tuqq=+



11122

Tqqαα=+



(20.1.51')

By a change of independent variable of the form (20.1.48), we obtain

()

12 1122

qq q qΛααβ

′′ ′ ′

=++++,

()

uT U hβ =++;

(20.1.51'')

there results the equations of motion

MECHANICAL SYSTEMS, CLASSICAL MODELS

242

∂

′′ ′

∂

′′ ′

−=

∂

αα

∂∂

=−

∂∂

(20.1.52)

The isoenergetic orbits (of energy

h ) are specified by the system (20.1.52), satisfying

the relation

()

qq β

′′

+=.

(20.1.52')

We obtain thus the normal form of the equations of motion of a generalized

conservative mechanical system with two degrees of freedom; these are the equations of

the plane motion of a particle subjected to a field of conservative forces of potential

and to a gyroscopic force

γv .

The method of calculation presented above may be used successfully also for

Liouville type systems, considered in Sects. 18.3.1.2 and 19.2.2.2, obtaining similar

results.

Let be a mechanical system with two degrees of freedom, of Lagrangian

()

12 12

qq Uqq=++



L .

(20.1.53)

In case of a conformal mapping

()

izq q fζ=+ = ,

iζξ ξ=+, where f is a

regular function in a convenient domain for

ζ , we may write ddzMζ= ,

()

Mfζ

′

= , so that

()

22 2

12 12

MWξξ ξξ=++



L ,

()()

12 12

,,WUqqξξ = .

(20.1.53')

Applying the method of change of independent variable, we find

()

22 2

MW hΛξξ

′′

=++ +,

(20.1.54)

with a condition of energetical nature

()

22 2

MW hξξ

′′

+= +.

(20.1.54')

For instance, the conformal mapping

z ζ=

corresponds to the study of the Keplerian

motion.

20.1.4 Maupertuis’s Principle. Other Variational Principles

In what follows, we will present Maupertuis’s principle in various forms, in the

general asynchronous case; as well, we will put into evidence the possibility to enounce

also other variational principles (for instance, the principle of the least potential action),

equivalent to Hamilton’s and Maupertuis’s principles.

Variational Principles. Canonical Transformations

243

20.1.4.1 Maupertuis’s Principle

We will introduce the kinetical action in the form

Tt q t

∂

∫∫



(20.1.55)

in the hypothesis of a conservative mechanical system and of catastatic constraints. We

mention that, often, one uses the quantity

A , called action. We admit also that

the mechanical energy is constant along any varied path; if

Eh= on the true curve,

then it results

EEhhΔΔ+=+ on a varied path.

Starting from the relation (20.1.42') and using the condition



L (we have

0TU==



), we find

qtt q

qt q

ΔΔΔ

∂∂

⎛⎞

⎜⎟

∂∂

⎝⎠

∫





Applying the operator

Δ to the relation (20.4.43'), we can write

ΔΔ Δ Δ

∂

⎛⎞

=−=

⎜⎟

∂

⎝⎠



so that

jj j

qhqtt q

qqtq

ΔΔ ΔΔ

∂∂ ∂

⎡⎛ ⎞ ⎤

−+ =

⎜⎟

⎢⎥

∂∂ ∂

⎣⎝ ⎠ ⎦

∫



 

LL L

;

using the relation (20.1.14), we get

()

111

222

qt q t t h

ΔΔ Δ Δ

∂∂

==+−

∂∂

∫





(20.1.55')

Besides, starting from the relation (20.1.43'') which takes place along the solutions of

Lagrange’s equations, and making

h=E , we have

()

tqhtt

ΔΔ Δ ΔΔ

∂

== −−

∂

∫



;

by means of the relation (20.1.43'), we obtain

()

[]

()

qt ht t q h t t

ΔΔ ΔΔΔ

∂∂

−−= −−

∂∂

∫





MECHANICAL SYSTEMS, CLASSICAL MODELS

244

and find again the relation (20.1.55'), in the same conditions.

Assuming that we have to do with varied paths with fixed ends, for which

0hΔ = ,

the constants being the same on all these paths (isoenergetic paths), it follows

TtΔΔ==

∫

A .

(20.1.56)

As a consequence of Lagrange’s equations, in the above mentioned conditions, this

relation represents a necessary condition for the motion on the true curve.

To put into evidence the sufficiency of this relation, we must show that, starting

from the relation (20.1.56), we obtain Lagrange’s equations. To do this, we must solve

a problem of extremum with constraints, of the form

FtΔ =

∫

()

FT Ehλ=+ −

, ETU=−,

where

()

tλλ= is a Lagrange multiplier. Using the relation (20.1.15) and equating to

zero the displacements

qΔ , 1,2,...,

s= , at the ends of the time interval, we may

write

jjj

FFF

Ft F q t q t

qqtq

ΔΔ δ

∂∂∂

⎛⎞⎡⎛⎞⎤

=− + −

⎜⎟ ⎜⎟

⎢⎥

∂∂∂

⎝⎠⎣⎝⎠⎦

∫∫





For the sake of simplicity, without loosing the generality, we will suppose that the

initial moment at

P is the same for all varied paths (

0tΔ = ),

tΔ being not fixed;

but we fix the co-ordinates

()

, 1,2,...,js= , so that we have (we observe that

TU h−=)

()

12 0

Fq T

∂

−=−+=

∂



for

tt=

. Using the basic lemma of the variational calculus, we obtain Euler–

Lagrange equations in the form

() ()

TTU

tq qq

λλλ

∂∂∂

⎡⎤

+−+=−

⎢⎥

∂∂∂

⎣⎦



, 1,2,...,js= ,

or in the form

() ()

112

jj j j

TTU T U

tq q q q q

λλλ

∂∂∂ ∂ ∂

⎡⎛ ⎞ ⎤

+−−=−−+

⎜⎟

⎢⎥

∂∂∂ ∂ ∂

⎣⎝ ⎠ ⎦





;

multiplying by



and summing for all indices j , we have

() ()

ddd d

112

ddd d

TTU T U

tq t t q t

λλλ

∂∂

⎡⎛ ⎞ ⎤

+−−=−−+

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦





Variational Principles. Canonical Transformations

245

where we took into account that

0UT==



, corresponding to the catastatic constraints

and to the condition



. Because the kinetic energy is a quadratic form, we can

write

()

1212

TU U

λλλ

−

+=−−+



;

taking into account that

TU h−=, we remain with

() ()

[]

212 12 0

λλ λ−−+ =− + =



Hence,

()

12Tλ+

is constant along the true curve; the condition imposed for

tt=

shows that this constant vanishes, so that

1/2λ =− at any moment. With this value of

λ , we see that the above Euler–Lagrange equations are just Lagrange’s equations of

motion.

One can thus state

Theorem 20.1.10 (Maupertuis). Among all possible motions of a mechanical system

subjected to catastatic ideal constraints, acted upon by conservative given forces, on

asynchronous varied isoenergetic paths with fixed ends, only and only the motion (of

the representative point on the true curve) which makes stationary the kinetic action

(20.1.56) takes place.

As in the cases considered in the previous Section, we can consider that this result is

a variational principle: the principle of the least action (Maupertuis’s principle). This

principle played an important rôle in the development of mechanics, being the first

variational principle of mechanics, enounced for the first time by P.L. Moreau de

Maupertuis in 1740 in a quite obscure form; this formulation led to a passionate

controversy, especially with S. Koenig, a controversy in which we mention also the

intervention of François Marie Arouet dit Voltaire (an adversary of Maupertuis). The

problem has been taken again by L. Euler (1744) who gave the formulation of the

principle in case of central forces; Lagrange (1760) and then Jacobi (1847) have given

its general form. Sometimes, the principle of least action is called also the Maupertuis-

Lagrange principle.

Obviously, for

0tΔ = we can enounce an analogous synchronous principle.

As we have seen, in case of catastatic constraints the relation (20.1.35') is reduced to

(20.1.45); comparing with Maupertuis’s principle, written in the developed form

()

TT tt

ΔΔ+=

∫

and eliminating the term

()

d/dTttΔ , we can state

Theorem 20.1.11 Among all possible motions of a mechanical system, subjected to

catastatic ideal constraints, on asynchronous varied paths with fixed ends, only and

only the motion (of the representative point on the true curve) which makes stationary

the kinetic action (20.1.56) with the condition

Tt tΔΔ=

∫∫

(20.1.57)

MECHANICAL SYSTEMS, CLASSICAL MODELS

246

takes place.

In case of quasi-conservative given forces, deriving from a simple quasi-potential,

we have

UUtΔΔ Δ=−



L , so that the condition (20.1.57) is reduced to

()

EUt tΔΔ+=

∫



;

(20.1.57')

if the forces are conservative, then there result

Eh=

and 0U =



, the condition

(20.1.57') being identically verified. We find again Maupertuis’s principle.

We observe that the Theorem 20.1.11 represents a generalization (larger conditions)

of the Theorem 20.1.10; obviously, we can affirm the same thing for the corresponding

variational principles.

Eliminating

between TU=+L and

TU h−=

, it follows 2Th=−L ;

from (20.1.38') and (20.1.55) we obtain, in this case,

() ()

10 10

ht t ht t=−−=−−

AA,

(20.1.58)

a relation connecting the kinetic and the Lagrangian actions. If

0t = and

tt= , we

find again the relation (19.2.15'), connecting the function

()St of the Hamilton-Jacobi

theory (to which corresponds

) to the function ()St, which appears in case of

generalized conservative mechanical systems (to which corresponds

A ,

according to the formula (19.2.17)).

20.1.4.2 Other Forms of the Least Action Principle

We can express the action 2

A also in the form

mv t

∑

∫

for a mechanical system

S of n particles

P , 1,2,...,in= ; Maupertuis enounced the

least action principle in the synchronous form

ii i

mv sδ

∑

∫

(20.1.59)

where

s is the curvilinear abscissa on the trajectory of the particle

P ,

S and

being the states of the system

S at the time

and

, respectively. Hence, the

elementary action

2dTt

is equal to the elementary work of the momenta of the

considered mechanical system

In case of a single particle

, we obtain

mv sδ =

∫

;

(20.1.59')

Variational Principles. Canonical Transformations

247

if on the particle does not act any given force, its motion will be uniform (as it results

from the study of the motion in an intrinsic frame of reference), so that

constv = , and

the relation (20.1.58') is reduced to

sδ =

∫

(20.1.59'')

The trajectory of the particle

P will be, in this case, a “geodesic line” in the constraint

conditions imposed to the motion. If the particle moves on a given fixed surface, then

the trajectory is a geodesic line on the respective surface, passing through the points

and

P . If there are not constraint relations, then the geodesic is a straight line and we

find again the principle of inertia.

Using the conservation theorem of mechanical energy, Jacobi eliminates the time in

the least action principle. Starting from

()

ii i

Tmv m

∑∑

we find

()

2d2d

TU h t T m sδδ δ

=+=

∑

∫∫

()

2d0

Uh msδ

=+ =

∑

∫

(20.1.60)

This synchronous form of the least action principle represents Jacobi’s principle and

has a pure geometric character; we observe that the integral

, in which the time

disappeared, can be calculated by means of any other parameter. As well, the condition

that the motion be isoenergetic on all varied paths becomes irrelevant; this is the great

advantage of this formulation. One observes that, using a Lagrangian of the form

()

2 TU hΛ =+, one obtains s differential equations of Euler–Lagrange type,

which are not independent; but they only allow to obtain the trajectory of the

representative point in the space

Λ . If we impose the condition TU h−=, then the

velocity on this trajectory is also determined.

In generalized co-ordinates, we have

ddd

ii ij i j

ms g qq

∑

so that

()

2dd

ij i j

Uhgqq=+

∫

A .

(20.1.60')

Replacing the mechanical system

S by a representative point P in the Lagrangian

space

, it is convenient to endow this space with the metrics

MECHANICAL SYSTEMS, CLASSICAL MODELS

248

ddd

ij i j

gqqσ = .

(20.1.61)

In the case in which the mechanical system is not subjected to any given force

(

constU =

), we can neglect a multiplicative constant, remaining the variational

condition

d0δσ=

∫

;

(20.1.61')

thus, we state

Theorem 20.1.12 (Jacobi). Let be given a discrete mechanical system S subjected to

holonomic, ideal constraints, which is acted upon by no one given force; the trajectory

of the representative point

P in the space

, endowed with the metrics (20.1.61), is a

geodesic line of this space.

As in Sect. 7.2.1.6, we can write the differential equations of the geodesic lines in the

form

[

]

jk k k l

gq kljqq

′′ ′ ′

+=, 1,2,...,

s= ,

(20.1.62)

where

[

]

,kl j is Christoffel’s symbol of the first kind; the differentiation is made with

respect to an arbitrary parameter, which can be even the curvilinear abscissa along the

trajectory of the representative point. Multiplying by the normalized algebraic

complement, summing and using Christoffel’s symbol of the second kind, there result

the equations of the geodesic lines in the normal form

qqq

⎧⎫

⎪⎪

′′ ′ ′

⎨⎬

⎪⎪

⎩⎭

, 1,2,...,js= ;

(20.1.62')

we notice the analogy which, obviously, does exists between these equations and the

normal form (18.2.47') of Lagrange’s equations, in which we make

∗

= ,

1,2,...,js= .

If the given forces are non-zero, hence if the potential

U is not constant, then we

introduce a manifold

Λ of metrics

()

d2 d dd

ij i j

Uh gqqσσ=+ = ,

()

ij ij

gUhg=+, ,1,2,...,ij s= ,

(20.1.63)

so that

d0δδσ==

∫

A .

(20.1.63')

We can thus state

Theorem 20.1.12' (Jacobi). Let be given a discrete mechanical system S subjected to

holonomic, ideal constraints and acted upon by conservative given forces; the

trajectory of the representative point

P , corresponding to the manifold

Λ and

endowed with the metrics (20.1.62) is a geodesic line of this manifold.

Variational Principles. Canonical Transformations

249

After obtaining the geodesic lines, the law of motion is given by

()

σσ

(20.1.64)

The Theorems 20.1.12 and 20.1.12' put in evidence the character of minimum of the

considered variational principle, as well as the denomination given to it. In fact, if the

functional is not minimized, it remains – at least – stationary.

20.1.4.3 The Analogy with Fermat’s Principle

From an optical point of view, a material medium is characterized by the refraction

index

(20.1.65)

where

c is the velocity of light in vacuum, while v is its velocity in the respective

medium. This index is a function of point (

()

123

,,nnxxx= ) in a non-homogeneous

medium; in an anisotropic medium, it is function also of direction. Let us consider a

medium, in general, non-homogeneous; the duration of light propagation is given by

(we take

0t = , by convention)

σ==

∫∫

where

dσ is the arc element, while s is the curvilinear co-ordinate along the path of

the light photon.

Corresponding to Fermat’s principle, among all paths which join two points of a

material medium, the light photon follows the shortest optical path, so that

nδσ=

∫

(20.1.66)

in a synchronous formulation. We find thus a formal analogy between this optical

principle and Maupertuis’s mechanical principle.

Using (20.1.60), we can write, for a single particle,

()

2d0

Uhsδ +=

∫

neglecting the factor

m . The trajectory of the light photon coincides with the

trajectory of the particle if

/2Un h=−. If we assume that, in the vicinity of the

Earth surface, the refraction index decreases linearly with the altitude

z , we can write

()

1/nn kzH=− , where H is the height of the atmosphere,

n is the refraction

index at the surface of the Earth, while

k is a constant. Neglecting

()

/zH with

respect to

/zH, we obtain

MECHANICAL SYSTEMS, CLASSICAL MODELS

250

Ucgz=− ,

cnh=−

(20.1.67)

hence the potential of a gravitational force in the proximity of the Earth surface, with a

conventional gravitational acceleration. Hence, if the refraction index

n has a linear

variation with the altitude, then the light is propagated along a parabola with a vertical

axis.

The refraction index will have the form

()

, ,...,

nnqq q= in the space

Λ , so

that we obtain for the photon a geodesic line in a manifold

of metrics ddnσσ= .

But the complete analogy between the two principles has been realized in 1924 by

Louis de Broglie in the frame of undulatory mechanics; he replaces the phase velocity

v by a group velocity u , so that

constuv =

. In this case, the principle (20.1.66) takes

the form

uδσ=

∫

(20.1.66')

analogous to the form (20.1.59') of Maupertuis’s principle for a particle.

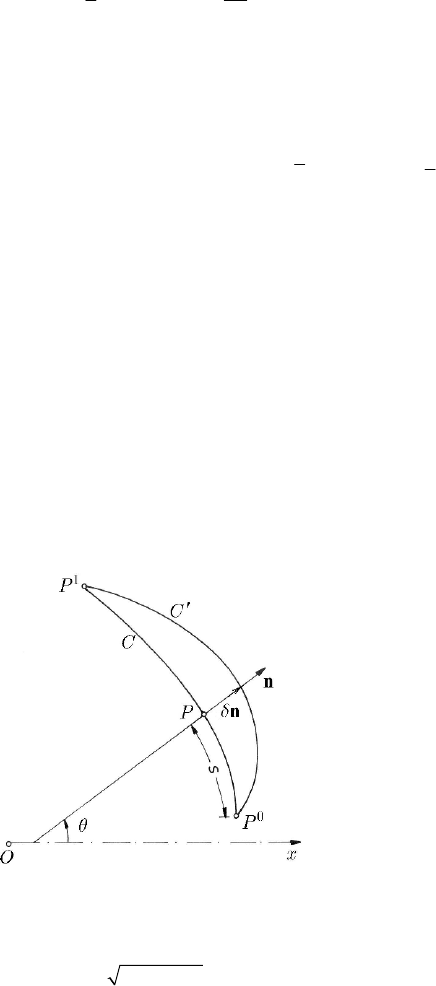
20.1.4.4 Plane Motion in a Field of Conservative Forces

In a plane motion of a particle on a curve C, we put in evidence the generalized co-

ordinates

s (the curvilinear co-ordinate, starting from the fixed point

P ) and θ (the

angle made by the external normal

n to the curve C with the fixed axis Ox (Fig.

20.3)). We assume that

()

ssθ= is an increasing function; if the curve is closed, then

it is also convex.

Fig. 20.3 Plane motion in a field of conservative forces

Let be the integral

()

IUhs=+

∫

;

if we pass from the curve C to the varied path

′

by a displacement ()nnsδδ= along

the external normal, we can write