Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Variational Principles. Canonical Transformations

251

()

d2 d

IsUhs

δδ=++

∫∫

We have

UNnδδ= , where N is the component of the field of forces along the

external normal, while

ddd/sn nsδδθδρ== , ρ being the curvature radius at the

point

P . We obtain thus

()

Ins

δδ=

∫

()

2 Uh

(20.1.68)

Writing the equation of motion along the external normal and taking into account the

mechanical energy conservation theorem, there results

/Nmvρ=−

()

2/Uhρ=− + , and we find again Jacobi’s form of the least action principle.

Let be a convex and closed simple curve C, and

C an analogous curve which

contains the first one. We can state

Theorem 20.1.13 (Whittaker). If a particle P which is in motion in the interior of a

ring formed by two conex and closed simple plane curves C (internal) and

C (external)

and is acted upon by conservative forces for which the potential

U has not

singularities in this ring, then it admits at least a periodic orbit if

0W < on C and

0W > on C .

20.1.4.5 Other Variational Principles

We will introduce, following V. Vâlcovici, a kinetic-potential energy

αβ

αβ=+E

(20.1.69)

()

,αβ kind and a corresponding kinetic-potential action

αβ αβ

∫

A E

(20.1.69')

of the same kind. To establish the conditions in which one can enounce an

asynchronous variational principle of the form

()

,, ,,

dd0

ttt

αβ αβ αβ αβ

ΔΔΔΔ ==+ =

∫∫

A EEE ,

we start from the general integral principle (20.1.35'), corresponding to the principle of

virtual work, the varied paths having fixed ends; subtracting the relation (20.1.35') from

the relation

()

TUTU tt

αΔ βΔ α β Δ+++ =

∫

we find the condition

MECHANICAL SYSTEMS, CLASSICAL MODELS

252

()

[]

{

}

12d0

TUWP t TU tt

αΔβΔΔ Δ α β Δ−+−+− +−+ =

∫

(20.1.70)

which allows the determination of the function

tΔ . In case of catastatic constraints

(

d/dPTt= ) and of quasi-conservative given forces ( WUUtΔΔ Δ=−



), we obtain

a much more simple form, i.e.

()

[]

{

}

11 2 d0

TUUtTUtt

αΔ βΔ Δ α β Δ−+−++−+ =

∫



(20.1.70')

If the given forces are conservative (

0U =



), then we can write a mechanical energy

conservation theorem (

ETUh=−=), so that the condition (20.1.70') becomes

()

[]

{

}

1222d0

hUhUtt

α Δ αβ Δ α αβ Δ−++− +−++− =

∫

(20.1.70'')

where we assumed that along a varied path we have

EEhhΔΔ+=+. Supposing

further that we have to do with isoenergetic varied paths (

0hΔ = ), this latter condition

has the form

()

2d 2 0

Ut h t tαβ Δ α Δ Δ+− + − − =

∫

(20.1.71)

or the form

()

[]

22d0

UhtΔαβ α+− + − =

∫

(20.1.71')

We can thus state

Theorem 20.1.14 Among all possible motions of a mechanical system, subjected to

catastatic, ideal constraints and acted upon by conservative given forces, on

asynchronous varied isoenergetic paths with fixed ends, only and only the motion (of

the representative point on the true curve) which makes stationary the action

,αβ

with the condition (20.1.71') takes place.

Obviously, in this case too, starting from this theorem, one can obtain a

corresponding variational principle.

In particular, for

2α = and

0β =

we find again the Theorem 20.1.10 of

Maupertuis. As well, for

1αβ== and

ttΔΔ= we find a particular form of

Voss’s principle; but we observe that, if we make

1αβ== in the condition

(20.1.70'), then we arrive at the form considered in Sect. 20.1.3.2.

Taking

0α =

and 2β = , as well as

ttΔΔ= , we obtain an asynchronous least

potential principle stated first by V. Vâlcovici and afterwards, in general conditions, by

P.P. Teodorescu) (the same duration on all varied paths)

Variational Principles. Canonical Transformations

253

UtΔΔ==

∫

A .

(20.1.72)

To can formulate a least mechanical action principle in the form

EtΔΔ==

∫

A ,

(20.1.73)

we must have

constE ≠ ; starting from the condition (20.1.70') and making

0αβ+=, we find (ETU=−, TU=+L )

()()

d2d0

EE tt Ut T tt

αΔ Δ ΔΔ Δ++−− =

∫∫



L .

The first variation vanishes, so that we can have a least mechanical action principle if

the condition

()

d2d

Utt T t t

ΔΔ Δ=+

∫∫



(20.1.73')

is verified; we find a more intricate relation (specifying

tΔ as a function of t ) as in the

previous case.

20.1.4.6 Larmor’s Principle

If some ignorable co-ordinates which not appear in the kinetic potential L do exist

(see Sect. 18.2.3.6), we can state a variational principle, in the frame of which appears a

functional which becomes stationary on a certain class of varied paths. We have thus to

do with a holonomic mechanical system with

s degrees of freedom, in which the first

r generalized co-ordinates are ignorable. Let thus be the functional

∂

⎛⎞

−

⎜⎟

∂

⎝⎠

∑

∫



Using the relation (20.1.43'''), we obtain the variation of this functional in the form

qt qq

qqq

ΔΔ Δ Δ

∂∂∂

⎡⎤

⎡

⎛⎞⎤

−− +

⎜⎟

⎢⎥

⎢

⎥

∂∂∂

⎣

⎝⎠⎦

⎣⎦

∑



LLL

jr k

qtq

ΔΔ Δ

=+ =

⎡⎤

∂∂

⎛⎞

=−−

⎜⎟

⎢⎥

∂∂

⎝⎠

⎣⎦

∑∑



The varied motion will be subjected to the restrictions (18.2.79'), with the same

constant as in the true motion. In this case (we calculate the derivative

d/dt under the

integral sign)

kjr

qt q t

ΔΔΔ

==+

⎡

⎤

∂∂

⎛⎞

−= −

⎢

⎥

⎜⎟

∂∂

⎝⎠

⎣

⎦

∑∑

∫





MECHANICAL SYSTEMS, CLASSICAL MODELS

254

By means of the relations (18.2.79') and by the normal procedure, we can express the

above integrand as a function of the constants

, ,...,

CC C and of the generalized

velocities

, ,...,

qq q

 

, obtaining thus the function R of Routh, which depends on

the palpable co-ordinates

, ,...,

qq q

Fixing the palpable co-ordinates at the ends of the time interval (not also the

ignorable co-ordinates) and fixing the initial and the final times (

0ttΔΔ==),

there results

dd0

Rt q t

ΔΔ Δ

∂

⎛⎞

==− =

⎜⎟

∂

⎝⎠

∑

∫∫



(20.1.74)

We may state

Theorem 20.1.15 (Larmor). Among all possible motions of a generalized conservative

mechanical system, subjected to ideal constraints, acted upon by quasi-conservative

given forces, on asynchronous varied paths with fixed ends (in space, for the palpable

co-ordinates, and in time), only and only the motion (of the representative point on the

true curve) which makes stationary the Routhian action (20.1.74) takes place.

This result can be considered as a generalization of the Theorem 20.1.8 and may be

used as a variational principle: Larmor’s principle.

Starting from this principle, we obtain – in the usual way – Routh’s equations.

20.1.5 Continuous Mechanical Systems

After some results with a general character, we consider some particular mechanical

systems; we will thus present the basic equations in the motion of strings, of straight

bars and of linear elastic solids.

We used till now analytical methods of calculus only to study discrete mechanical

systems (with a finite number of degrees of freedom); in case of an infinite number of

degrees of freedom, the problems impose a specific treatment. For instance, in case of

vibrations of an elastic solid, every one of its point participates at this motion; the

motion may be described only if all parameters which indicate the position of each

point are involved.

20.1.5.1 Lagrangian Formalism

To put into evidence the treatment of the problem, we will start from a continuous

mechanical system, which will be studied – at the beginning – by discrete methods in a

Lagrangian formalism.

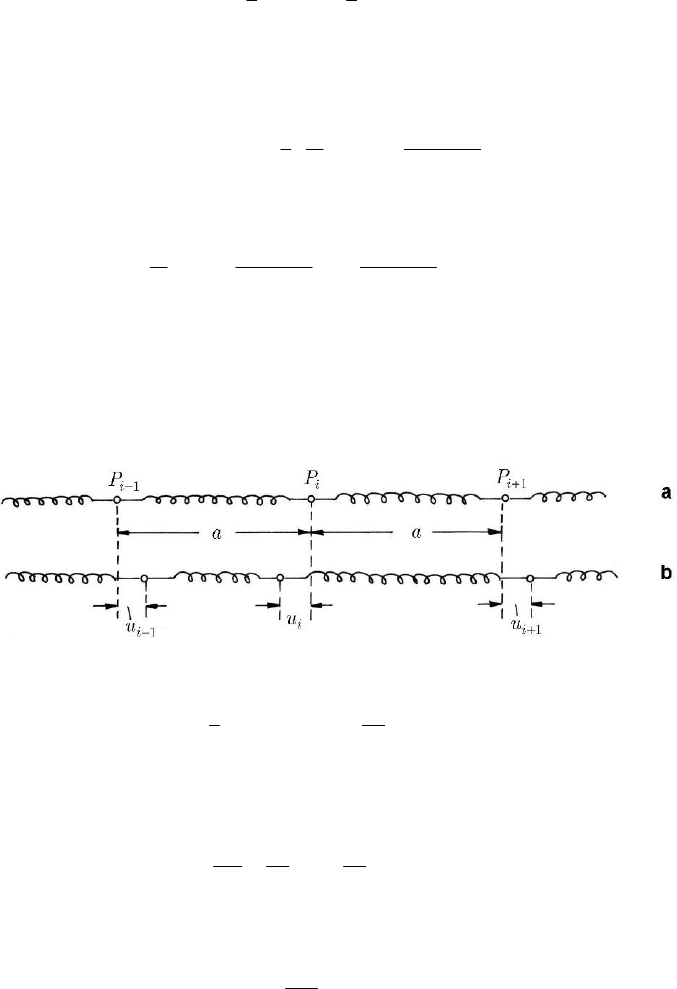
Let be a linear elastic, isotropic and homogeneous straight bar (see Sect. 12.1.1),

subjected to longitudinal small motions; it can be approximated (mathematically

modelled) by a discrete system of particles

P of equal masses m along the axis,

separated at equal distances

a (in a position of equilibrium) by springs of elastic

constants

k (Fig. 20.4a); during the motion, the particle

P has a displacement

along the bar axis, so that

()

uut= (Fig. 20.4b). As a matter of fact, we study thus a

linear polyatomic molecule (case in which the number of particles is finite). We obtain

thus the Lagrangian

Variational Principles. Canonical Transformations

255

()

TU mu ku u

=+= − −

∑∑

L ,

the forces which act on those particles (because of the springs at left and right) being

()()

ii i

Fkuu kuu

−+

=− − + − . We may also write

∑

LL,

(

)

uka

−

⎡

⎤

=−

⎢

⎥

⎣

⎦



L ;

there result Lagrange’s equations

uu uu

uka ka

+−

−−

−+=

In a process of passing to limit, /ma tends to the density μ ,

()

uua

− tends to

the linear strain

ε ,

F tends to the force F , while k tends to the rigidity of axial

forces

EA , where E is the longitudinal elasticity modulus and A is the area of the

cross section (

FEAε= ). In this case, the kinetic potential will be (for a bar of length

l )

Fig. 20.4 Discrete model of a linear elastic, isotropic, homogeneous straight bar

()

xuEAx

∞

−∞

∂

⎡

⎤

=−

⎢

⎥

∂

⎣

⎦

∫∫

L ,

(20.1.75)

where

()

;uuxt=

and x is the abscissa along the bar axis; observing that, by passing

to the limit,

() ()

xxa

EA u u

ax x

−

∂∂

⎡

⎤

−

⎢

⎥

∂∂

⎣

⎦

leads to

()

/EA u x∂∂, we find the equation of motion

uEA

∂

−=

∂



(20.1.75')

So, characteristic aspects of passing from discrete to continuous systems are put in

evidence. As one can see, the position co-ordinate

x is not a generalized one; it plays

MECHANICAL SYSTEMS, CLASSICAL MODELS

256

the rôle of a continuous index, replacing the numerable index

i . As to every index i

corresponds a generalized co-ordinate

u , so to every x corresponds a generalized co-

ordinate

()ux ; taking into account also the dependence on time, we must have

()

;uuxt=

. In the above conditions, L is – in fact – a Lagrangian density; in what

follows we will use the notation

L (as for the Lagrangian), because only the

Lagrangian density plays a rôle in describing the motion of the mechanical system.

The motion of a three-dimensional continuous mechanical system, which occupies

the domain

Ω , will be described – in general – by means of the Lagrangian

Ω

∫

L ,

()

123 123

,,,,;,,;uu u u ux x x t= LL ,

(20.1.76)

where L is the Lagrangian density, while /

uux=∂ ∂ , 1,2,...,in= , /uut=∂ ∂



123

,,,xxxt being independent variables. Hamilton’s principle in a synchronous case is

written in the form

dd0

Ω

δΩ=

∫∫

L .

(20.1.76')

We notice that, in this case, the parameters

123

,,,xxxt have not variations, the

variation process having no influence neither on the integration domain

Ω , nor on the

integration limits with respect to time; thus,

uδ will vanish on Ω∂ as well as for

and

t . On the basis of the results in Sect. 20.1.1.3, we can write Euler-Ostrogradskiĭ

equations

tu x u u

∂∂∂

⎛⎞

+−=

⎜⎟

∂∂∂

⎝⎠



LLL

(20.1.77)

where we use the summation convention of dummy indices. Instead of

s differential

equations of second order for a discrete mechanical system, in case of a continuous one

we find a partial differential equation in four variables:

123

,,xxx, and t . In general,

we may have several types of displacements

()

123

,,;uuxxxt

αα

= ,

1,2,...,mα =

;

for instance, in case of vibrations of an elastic solid we have

3m = . One obtains the

equations of motion

tu x u u

ααα

∂∂∂

⎛⎞

+−=

⎜⎟

∂∂∂

⎝⎠



LLL

, 1,2,...,mα = .

(20.1.78)

Introducing the functional derivative (the variational derivative – an extension of the

Euler–Lagrange derivative)

uu u

αα α

∂∂

=−

∂∂

(20.1.79)

and observing that

//uu

αα

δδ=∂ ∂LL,

1,2,...,mα =

, we can write the equations

of motion also in the form

Variational Principles. Canonical Transformations

257

dtu u

αα

δδ

⎛⎞

−=

⎜⎟

⎝⎠



1,2,...,mα =

(20.1.79')

similar to that of Lagrange’s equations.

20.1.5.2 Hamiltonian Formalism

To put in evidence the possibility of using the Hamiltonian formalism, we take again

the example considered at the preceding subsection by discretization. We introduce thus

the generalized momenta

∂

∂∂



and build up the Hamiltonian

ii i i i

ii i

Hpu au au

∂∂

⎛⎞

=−= −= −

⎜⎟

∂∂

⎝⎠

∑∑ ∑

 



LL L

Using the same process of passing to limit and introducing the Lagrangian density

L ,

we obtain the Hamiltonian

dHux

∞

−∞

∂

⎛⎞

=−

⎜⎟

∂

⎝⎠

∫



;

we are thus led to use further the notion of density.

In the motion of a three-dimensional continuous mechanical system which occupies

the domain

Ω and the position of which is specified by m generalized co-ordinates

()

123

,,;uuxxxt

αα

= , 1,2,...,mα = , we introduce the generalized momenta

density

∂

∂ 

(20.1.80)

hence, the Hamiltonian density

αα

=−

∑



L ,

(20.1.81)

of the form

()

123 123

,,,,,;,,;uuuuu xxxt

αααααα

π= 

H . Hamilton’s function is

thus given by

αα

ΩΩ

Ωπ Ω

⎛⎞

== −

⎜⎟

⎝⎠

∑

∫∫

HL,

(20.1.81')

so that

MECHANICAL SYSTEMS, CLASSICAL MODELS

258

dddddd

Hu ut

ααα

Ω

πΩ

∂∂

⎡⎤

⎛⎞

=+++

⎜⎟

⎢⎥

∂∂∂

⎝⎠

⎣⎦

∂

∑

∫



HHH

Integrating by parts and using the same procedure as in Sect. 20.1.1.3, we obtain

dddddd

Hu ut

uxu

αα α

Ω

πΩ

∂∂ ∂

⎧⎫

⎡⎛⎞⎤

=+++

⎨⎬

⎜⎟

⎢⎥

∂∂ ∂

⎣⎝⎠⎦

⎩⎭

∑

∫



HH H

dddd

αα

Ω

πΩ

∂∂

⎡⎤

⎛⎞

=++

⎜⎟

⎢⎥

∂∂

⎝⎠

⎣⎦

∑

∫



where we used the notation (20.1.79) and observed that //

αα

δδπ π=∂ ∂HH. If we

differentiate, starting from the second form (20.1.81'), we can write (we use the

functional derivative)

d d+ddddd

Huuuut

αα αα α α

αα

Ω

δδ

ππ Ω

δδ

⎡⎤

⎛⎞

=−−−

⎜⎟

⎢⎥

⎝⎠

⎣⎦

∑

∫

 



;

the notation (20.1.80) and the equations (20.1.79'), written in the form



, =

δ 

(20.1.82)

lead to

()

ddddd

Huut

αα αα

Ω

ππ Ω

⎡⎤

=−+−

⎢⎥

⎣⎦

∑

∫





L .

Comparing the two expressions of

dH , we find the equations of motion

δπ

=

=−

(20.1.83)

analogue to Hamilton’s equations, as well as the relation

=−



(20.1.83')

In a developed form, we have

∂



uxu

αα

∂∂

⎛⎞

=− +

⎜⎟

∂∂

⎝⎠



(20.1.83'')

obtaining a form which has no more a symmetric character.

The canonical form of Hamilton’s synchronous principle will be

()

123 123

,,,,;,,; dd 0

u uuuu xxxt t

αα ααααα

Ω

δπ π Ω

⎡⎤

−=

⎢⎥

⎣⎦

∑

∫∫

 H .

(20.1.84)

Variational Principles. Canonical Transformations

259

We may calculate

αα

Ω

πΩ

∂∂

⎡⎤

⎛⎞

=++

⎜⎟

⎢⎥

∂∂

⎝⎠

⎣⎦

∑

∫





;

with the aid of the equations of motion (20.1.83) we observe that, along the

corresponding integral curves, we obtain

Ω

Ω=

∫



(20.1.85)

Hence, the Hamiltonian

H is conserved in time if the Hamiltonian density

does

not depend explicitly on time (



In general, let be the functional

Ω

Ω=

∫

F ,

(20.1.86)

where

()

123 123

,,,,,;,,;uuuuu xxxt

αααααα

π= FF . We can write

αα

Ω

πΩ

∂∂

⎡⎤

⎛⎞

=++

⎜⎟

⎢⎥

∂∂

⎝⎠

⎣⎦

∑

∫





;

taking into account the equations of motion (20.1.83), there results

tu u

αα αα

Ω

δδ δδ

Ω

δδπ δπδ

⎡⎤

⎛⎞

=−+

⎜⎟

⎢⎥

⎝⎠

⎣⎦

∑

∫



FH FH

(20.1.87)

We observe thus that we obtain a quantity similar to the Poisson bracket; using an

analogous notation, we may write

()

Ω

⎡⎤

⎣⎦

∫



FH F

(20.1.87')

We may thus affirm that

F is conserved in time if simultaneously

()

,0=FH and



; one can also say that F is a constant of motion. The conservation theorems

for integral quantities can be obtained as in the previous chapter, and one can develop

analogous methods of calculation. But we must observe that, besides the theorems

concerning “macroscopic” constants of integration (for integral quantities), one can

state theorems for “microscopic” such constants (for densities); the latter results are of a

special interest in mechanics of continuous deformable media.

We remark that all the above considerations may be used also for a field description

with the aid of variational principles (even in the absence of a mechanical system).

20.1.5.3 Motion of Linear Elastic Solids

To determine the density

L of the Lagrangian in case of a linear elastic solid, we

must calculate the densities

T and V of the kinetic energy, and of the potential energy,

respectively, so that

MECHANICAL SYSTEMS, CLASSICAL MODELS

260

Ω

Ω=

∫

Ω

Ω=

∫

;

(20.1.88)

to do this, we need some preliminary considerations.

Let

()

000

123

,,;fxxxt be a function of class

C , expressed by means of material co-

ordinates; using spatial co-ordinates, we obtain the function in the form

()

123

,,;fxx x t (see Sect. 12.1.1.1). The partial derivative of first order with respect to

one of the variables, e.g. the variable

x , is written in the form

123

00 0 00

123

11 1 11

uuu

ff f f f

xx xx

xx x xx

∂

∂∂∂

∂∂ ∂ ∂ ∂

⎛⎞

==+++

⎜⎟

∂∂ ∂∂

∂∂ ∂ ∂∂

⎝⎠

(20.1.89)

where we took into account (12.1.3''),

u ,

1, 2, 3

, being the components of the

displacement vector; neglecting the displacement gradient (the tensor

ij j

uxα =∂ ∂ ,

,1,2,3ij=

) with respect to unity, one has

∂

(20.1.89')

Hence, in this case, we obtain the same results, in the same form, either we use material

or spatial co-ordinates.

The symmetric part of the tensor

α is the strain tensor (

(,)

uε =

()

(,)

ij ji

uu α=+ =); if ij= one obtains the linear strains, while if ij≠ ,

ij ij

γε= , ,1,2,3ij= , represent the angular strains. The hypothesis of neglecting

the displacement gradient with respect to unity includes thus the case of infinitesimal

deformations, case in which the relations between strains and displacements are linear.

The antisymmetric part of the tensor

is the local rotation of rigid body tensor

(

[,]

uω =

()

[,]

ji ij

uu α=− =) is also neglected with respect to unity (as the

displacement gradient). We may thus speak about a linear theory from a geometric

point of view (case in which relations of the form (20.1.89') hold).

Taking into account the notions introduced in Sect. 12.1.1.1, from relations (12.1.2'')

and (12.1.3'') we obtain the velocity and the acceleration (in spatial description)

tx t

∂∂

== +

∂∂

uu u

txt

∂∂

== = +

∂∂

vuv v

(20.1.90)

for a point of the solid; the vector

r (corresponding to the initial moment) is constant.

Neglecting the non-linear terms, we remain with the displacement velocity (neglecting

the spatial derivative, the total derivative is reduced to the time one)

∂



(20.1.90')