Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems
Подождите немного. Документ загружается.

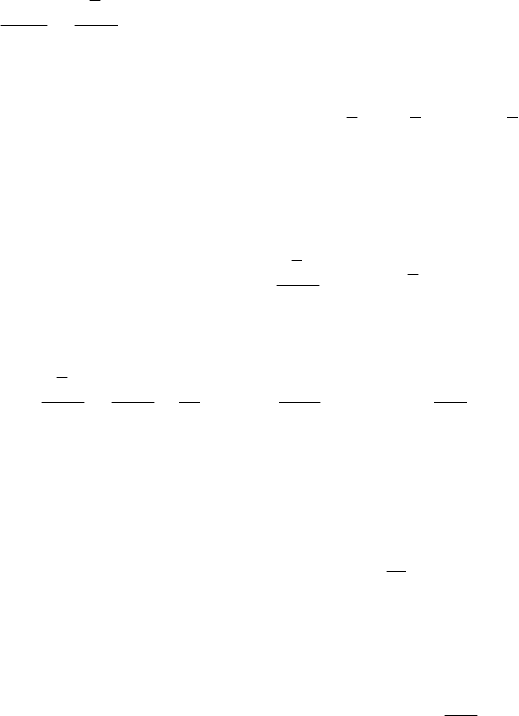
MECHANICAL SYSTEMS, CLASSICAL MODELS
same pole by the angular velocity vector of the non-inertial frame
R with respect to
the inertial frame
′
R ), the moment of momentum of the mass centre, translated at the
pole
O, at which is considered to be concentrated the whole mass of the system S, with
respect to the pole
O
′
, in the frame
′
R , and the moment of momentum of the pole O,
translated at the centre of mass at which is assumed to be concentrated the whole mass
of the system
S, calculated with respect to the pole O, in the same inertial frame
′
R .
Differentiating the relation (11.2.16) with respect to time in the fixed frame, we can
write
[]
d
d
()
dd
OO
OCOC CO O O
M
tt
′
′
′′′′ ′ ′ ′
=+ ×+×+×+××+×
K
K
vvra vv v aωρ ρ
;
observing that
OO
O
′
′
=+×MMrR
,
OO
O
′
′
=+×MMrR
for the moments of the given and constraint external forces and taking into account
(11.2.14), (11.2.15), V. Vâlcovici showed that the theorem of moment of momentum
becomes
d
()
d
O
OOO
M
t
′
×+=+
K
aMMρ ,
(11.2.18)
where
dd
d
() ()
ddd
OO O O
OOOO
ttt t t
∂∂
=+ =+×+ ++×
∂∂
KK K I
IKIIωω ωωωω
.
(11.2.18')
Observing that
() ()2()()()
iiiiii iiii
×× +×× = ⋅ −⋅ −⋅rvvrrv vrrvωω ωωω
()()
() () () () () () () () () ()
2
ii ii ii ii ii
j
j
j
kkjkk
jj j
ll k k ll k
xx xx xx xx xx
t
δωδω
∂
=−− = −
∂
ii
,
multiplying by
i
m , summing for all the particles of the discrete mechanical system S
and introducing the tensor of inertia, we find the remarkable relation
11
() ()
nn
O
ii i i i i
ii
mm
t
==
∂
×× + ×× =
∂
∑∑
I
rv vrωωω
,
(11.2.18'')
corresponding to the relation (11.2.17).
Starting from the equations of motion (11.2.13), (11.2.13'), we effect a vector
product at the left by
i
r and sum for all the particles of the system S ; we get thus
62
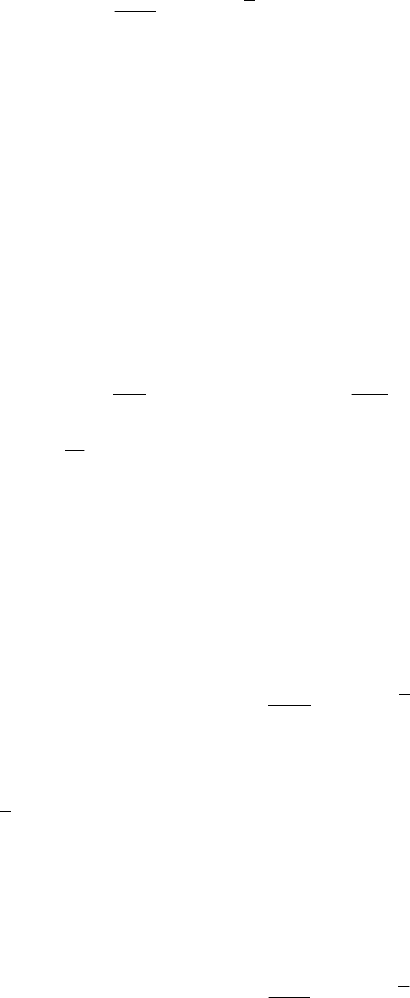
()
() ()
1
n
ii
O
i
OO
t
C
i
t
=
∂
=++ × +
∂
∑
K
MM rF F
.
(11.2.18''')
We notice that
1
() ( ) ( )
n
ii i
OO O
i
Mm
=
′
+× +× = × ×
∑
II a rr
ωω ω ρ ω
()
111
()
nnn
i
ii i ii i
O
t
iii
mm
===
′
+ × × × + × =− ×
∑∑∑
rr ra rFωω ,
because
[
]
[
]
()()() ()
ii iii i
××× =−⋅ ×=×××rr rrr rωω ωω ωω,
as well as (we use the relation of definition (3.1.81))
() ()
1 1
n n
jk
ii
O
mn
ii i j i j
Okjkllmnk
i i
I
m mxv
tt
ω ω
= =
∂
∂
×+ =× ×+ =∈∈
∂∂
∑ ∑
I
Krvi iωωω
()
()
() () () () () ()
1 1
n n
ii ii ii
pp mn
ijjmjnij
kjk knkmk
j
k
i i
mxx xx mxv
t
ωδ δδδδω
= =
∂
+−=−
∂
∑∑
ii
()()
() () () () () () () () () ()
11
22
nn
ii i i ii ii ii
pp pp
ijijj
kjk k
jj j
kk k
ii
m xv vx xv mxv xvωδ ωω
==
+ −−=−
∑∑
ii
[]
()
111
2()()2 ()
nnn
i
iii i i ii i i
C
iii
mm
===
=⋅−⋅=××=−×
∑∑∑
rv r v r v r Fωω ω ;
one can thus state that the relations (11.2.18) and (11.2.18''') are equivalent.
One can easily see that the theorem of moment of momentum (11.2.18) reads
d
()
d
O
OOO
M
t
′
×+=+
K
aMMρ
(11.2.18
iv
)
if we have
const
O
O
==
J
JJJJG
KIω
with respect to the inertial frame
′
R .
In the particular case in which the frame
R does not rotate ( = 0ω , hence
OO
=KK), it results the formula
() ()
OO C O
O
MM
′
′′′ ′
=+× +×KKr v v
ρ
,
(11.2.19)
obtained by V. Vâlcovici as a particular case of the Theorem 11.2.7; the theorem of
moment of momentum becomes
()
O
OOO
M
t
∂
′
×+=+
∂
K
aMMρ
(11.2.19')
and we can state
11 Dynamics of Discrete Mechanical Systems
63
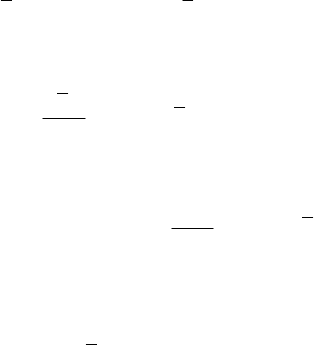
MECHANICAL SYSTEMS, CLASSICAL MODELS
Theorem 11.2.8 (V. Vâlcovici). The theorem of moment of momentum of a free discrete
mechanical system maintains its form with respect to a non-inertial frame of reference
which does not rotate (it moves with the axes parallel to themselves) if, from the
moment of the given and constraint external forces, we subtract the dynamic moment
(with respect to an inertial frame) of the pole of the non-inertial considered frame,
translated at the centre of mass of the system, at which is assumed that is concentrated
the whole mass of the system, with respect to this pole.
One can thus see that the theorem of moment of momentum of a free or constraint
discrete mechanical system maintains its form with respect to a non-inertial frame of
reference which does not rotate if and only if
O
′
×=a0
ρ
, hence in one of the
following cases: (i) the pole of the non-inertial frame has a uniform and rectilinear
motion with respect to an inertial frame, the movable frame being thus inertial too;
(ii) the non-inertial frame is a Koenig frame (
= 0
ρ
, hence
OC≡
, Theorem 11.2.4);
(iii) the support of the acceleration
O
′
a
of the pole of the non-inertial frame, with
respect to an inertial frame, passes always through the centre of mass
C. As a matter of
fact, the case (ii) is a particular case of (iii).
We say that a non-inertial frame
R is a frame of Koenig type if = 0ω but its pole
is not the mass centre; in this case, the frame
R is just such a frame. As it was shown
by V. Vâlcovici, to can write a formula of Koenig type
()
OO O
O
M
′
′′′
=+×KKr v
(11.2.20)
it is necessary and sufficient that (we notice
COC
′′
=+vvv
)
() ()
OC O
MM
′′
×+×=rv v0
ρ
.
(11.2.20')
In the particular case in which the pole of the non-inertial frame coincides with the
centre of mass of the system (
OC≡ , = 0
ρ
), we obtain a formula of Koenig type
()
CC
O
M
′
′′′
=+×KK vρ
,
C
CC
=+KKK,
(11.2.21)
and the theorem of moment of momentum reads
d
d
C
CC
t
=+
K
MM
;
(11.2.21')
if we have
= 0ω too, then the non-inertial frame R is a Koenig one, so that
()
CC
O
M
′
′′′
=+×KK v
ρ
,
C
CC
t
∂
=+
∂
K
MM
.
(11.2.22)
Taking into account the results in Sect. 11.1.2.3, we notice that we may write
()
OOC
O
M
′
′′′ ′
=×KKr v−
; the formula (11.2.16) takes thus the form
()
OO O
M
′′
=+×KK vρ ,
(11.2.23)
64

the moment of momentum
O
′
K
being calculated with respect to the inertial frame
′
R .
Analogously, we can write
() () ()
OC CO C C C
MM M
′′′ ′′ ′ ′ ′
=+× −× =+×KK v r v K v
ρρ
,
with respect to the inertial frame, as well as
()
OC C
M=+×KK v
ρ
, with respect to a
non-inertial frame. Taking into account (3.1.116'), (11.2.14) and (11.2.17') and
observing that
()
()
OC
M=× ×I S
ρ
ω
ρ
, we can write the relation (11.2.23) in the
form
()
C
CCC CC
′
==+=+KKKKKI
S ω ,
(11.2.23')
stating
Theorem 11.2.9 (C. Iacob). The moment of momentum of a discrete mechanical system
with respect to the centre of mass, in an inertial frame of reference
′
R , is equal to the
moment of momentum of this system with respect to the centre of mass, calculated in a
non-inertial frame
R of Koenig type (the sum of the moment of momentum of the
system with respect to the centre of mass, in an arbitrary non-inertial frame
R, with
the same pole as
R , and the contracted product of the tensor of inertia, with respect
to the same pole, by the angular velocity vector of the frame
R, with respect to the
frame
′
R ).
The privileged rôle of the centre of mass is thus put into evidence. If
= 0ω , the
arbitrary non-inertial frame
R being in motion of translation with respect to the inertial
frame, then we get
CC
′
=KK
;
(11.2.23'')
this result corresponds to the relation (11.2.19) of V. Vâlcovici. If, in particular, the
pole of the non-inertial frame coincides with the centre of mass, then we can write the
relation
()C
C
C
′
=
KK
,
(11.2.23''')
which corresponds to the Theorem 11.2.1 of Koenig.
If in the formula (11.1.23) we take
QC≡ , then the theorem of moment of
momentum reads
()()
ddd
d
dddd
CCC
CCC
tttt
′
==+ =+
KKK
IMM
S ω ,
(11.2.24)
where we took into account (11.2.23'); we mention that the derivatives are calculated
with respect to the inertial frame
′
R . If = 0ω , then it results
C
CC
t
∂
=+
∂
K
MM
,
(11.2.24')
11 Dynamics of Discrete Mechanical Systems
65
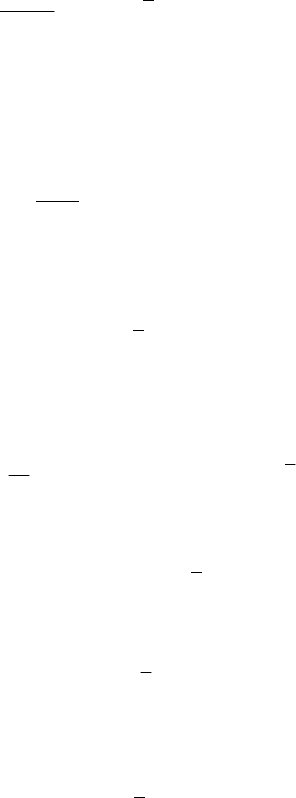
MECHANICAL SYSTEMS, CLASSICAL MODELS
the derivative being calculated with respect to the non-inertial frame
R with the pole at
O, while if, in particular, OC≡ , then we obtain
()C
C
CC
t
∂
=+
∂
K
MM
,
(11.2.24'')
the non-inertial frame being with the pole at the centre of mass; this last result
corresponds to the Theorem 11.2.4 of Koenig.
Introducing the dynamic moment (11.1.67) and taking into account (11.1.23) and
(11.1.67'), we get
d
()
d
O
OOC
M
t
′
′′′
=+×
K
Dvv
.
(11.2.25)
Using the relation (11.2.23), we find again the theorem of dynamic moment in the
inertial frame
′
R , with respect to an arbitrary pole O, in the form
OOO
′
=+
DMM.
(11.2.25')
Taking into account the relations (11.2.18), (11.2.18'), we can write this theorem in the
non-inertial frame of reference
R too; we obtain
d
() ( )
d
OOO OOO
M
t
′
+× + +× = +DKI aMMωωρ
.
(11.2.25'')
If
= 0ω , then it results
()
OOOO
M
′
+× = +DaMMρ ,
(11.2.25''')
corresponding to the Theorem 11.2.8. If we have
OC≡ too, then we can write
()C
CC
C
=+DMM,
(11.2.26)
which corresponds to the relation (11.2.24''); starting from the relation (11.2.24'), it can
be easily verified that
CCC
=+DMM,
(11.2.26')
with respect to an arbitrary non-inertial frame with the pole at
O. From (11.2.11') to
(11.2.25') it results also a theorem of dynamic torsor in an inertial frame with respect to
an arbitrary pole
{
}
{
}
{
}
ii i
OOO
′
τ=τ+τAFR
.
(11.2.27)
66

We notice that, starting from the theorem of momentum, one can obtain conservation
theorems (hence, first integrals) only with respect to the inertial frame
′
R . Thus, if
RR 0+=
, then from (11.2.15) it results that
C
′
=a0
, wherefrom
C
′
=vC
,
t
′′
+CC
ρ
= , ,const
′
=
J
JJJJG
CC
, with respect to the frame
′
R .
In what concerns the theorem of moment of momentum with respect to the pole of a
non-inertial frame of reference
R, one can make some interesting considerations. Thus,
if
O
′
×=a0
ρ
, hence if the support of the acceleration of the pole O with respect to an
inertial frame passes through the centre of mass of the discrete mechanical system
S
(we eliminate the trivial case in which the pole
O has a uniform and rectilinear motion
with respect to a frame
′
R , hence the case in which the frame R is inertial too, as
well as the case in which
OC≡
), and if the sum
OO
+=MM 0, then
const
O
=
J
JJJJG
K
,
the moment of momentum
O
K (calculated with respect to the non-inertial frame R )
being conserved in time with respect to the inertial frame
′
R ; one obtains thus a
vector first integral. If we have
= 0ω too (the non-inertial frame R does not rotate
with respect to the inertial frame
′
R ), then const
O
=
J
JJJJG
K
(the moment of momentum
with respect to the pole
O, in the frame R , is reduced to the moment of momentum
with respect to the same pole, in the frame
R ) with respect to the non-inertial frame
R.
If in the relation (11.2.24) we make
CC
+=MM 0, then it results const
C
′
=
J
JJJJG
K
,
the moment of momentum
C
′
K
(calculated with respect to the non-inertial frame R )
being conserved in time with respect to the inertial frame
′
R ; we notice that this result
cannot be obtained from the above one, making
OC≡ , because it takes place with
respect to an arbitrary non-inertial frame
R. If we have = 0ω too, then
const
C
=
J
JJJJG
K
with respect to the non-inertial frame R, and if, in particular, OC≡ , then
()
const
C
C
=
J
JJJJG
K
with respect to a non-inertial frame with the pole at the centre of mass
(this last first integral can be obtained from the Theorem 11.2.4 of Koenig).
As a conclusion, one can obtain a vector first integral (equivalent to three scalar first
integrals) with respect to a non-inertial frame too, but which is not independent of that
which can be obtained with respect to an inertial frame.
11.2.2.2 Kinetic Energy and Work with Respect to an Arbitrary Non-inertial
Frame of Reference. Comoment of Two Torsors
Squaring the relation (11.2.10'), we can write
22 2
()2()()
ii iiii
OOO
′′′
++× = + ⋅ +×+ +×
vv r v vv r v rωωω.
Multiplying by
i
m and summing for all the particles of the discrete mechanical system
S, it results (we take into account (11.2.14))
11 Dynamics of Discrete Mechanical Systems
67

MECHANICAL SYSTEMS, CLASSICAL MODELS
22
11
(,,)
22
OOC O OOC
TT Mv M M T Mv M
′′′ ′ ′′′
=+ + ⋅ + =− + ⋅vv v vvωρ ,
(11.2.28)
where we have introduced a quantity of the nature of a kinetic energy
()
2
2
11
d
11
()
22d
nn
i
ii i i
ii
Tm m
t
==
=+×=
∑∑
r
vrω
,
(11.2.28')
which, as in the case of the moment of momentum, does not represent the kinetic
energy of the discrete mechanical system
S with respect to the non-inertial frame;
indeed, the derivative of the position vector
i
r , in the non-inertial frame R, is taken
with respect to the inertial frame
′
R . This quantity, which is – in fact – the kinetic
energy of the discrete mechanical system
S with respect to the non-inertial frame R ,
becomes
()
1
2
O
OO O
TT T T=+ ⋅ + =+⋅ +KK Kωω,
(11.2.28'')
where
2
1
1
2
n
ii
i
Tmv
=
=
∑
(11.2.28''')
is the kinetic energy of the discrete mechanical system
S with respect to the non-
inertial frame
R, while
()
222
11 22 33
111
()
222
O
j
Ojkk
TIIIIωω ω ω ω=⋅ = = + +Iωω ;
(11.2.29)
we have put thus in evidence also the representation with respect to the principal axes
of inertia, that is a quantity of the nature of a kinetic energy, which we call
pseudokinetic energy, of the discrete mechanical system
S with respect to the non-
inertial frame
R having the pole at O. We state
Theorem 11.2.10 (V. Vâlcovici). The kinetic energy of a discrete mechanical system
with respect to a given inertial frame of reference
′
R is equal to the sum of the kinetic
energy of this system with respect to an arbitrary non-inertial frame
R , which does
not rotate with respect to the frame
′
R (the sum of the kinetic energy of the system
with respect to a non-inertial frame
R with the same pole O as the frame R , the
scalar product of the angular velocity vector by the moment of momentum of the system
with respect to the same pole, in the same frame
R, and the semi-scalar product of the
angular velocity vector by the contracted product of the tensor of inertia with respect to
the pole
O by the angular velocity vector) and the scalar product of the velocity of the
pole
O with respect to the frame
′
R by the momentum of the system with respect to
68

the same frame
′
R , from which the kinetic energy of the pole O, in the frame
′
R ,
where the whole mass of the discrete mechanical system is considered to be
concentrated, is subtracted.
If
()tω is along the direction Δ of unit vector n at the moment t, then we can write
22
11 1
() ()
22 2
OO
I
Δ
ωω⋅=⋅ =InInωω ,
(11.2.29')
where we have taken into consideration (3.1.82'),
()tωω= being the magnitude of the
angular velocity of instantaneous rotation; the axial moment of inertia
I
Δ
plays thus
the rôle of a mass for the instantaneous motion of rotation.
Taking into account (11.1.16), we find also the remarkable solution
()
11 1
()
22 2
OCOOOC
O
TT M M
′
′′ ′′′′
=+ ⋅ + + ⋅ −× + ⋅KK vv r vvωω
.
(11.2.30)
The elementary work of the given and constraint external and internal forces which
act upon the discrete mechanical system
S is given by
int
int
111
dd d d ( )d '( )d
nnn
ii i i
RR ikik
iik
WW W W
===
′′ ′ ′ ′ ′
++ + = +⋅+ +⋅
∑∑∑
FR r F R r
111 1
() '( )d()d
nnn n
ii ii i
ik ik O
iik i
=== =
⎡⎤
′
=++ +⋅++⋅
⎢⎥
⎣⎦
∑∑∑ ∑
FR F R r FR r
11 1 1
'( ) d '( ) d
nn n n
iiii
ik ik ik ik
ik i k
t
== = =
⎡
⎤
++⋅+×⋅+++
⎢
⎥
⎣
⎦
∑∑ ∑ ∑
FR r rFR FRω ,
where we have used the formula (11.2.10'); introducing the torsor of the given and
constraint external forces at the pole of the non-inertial frame
(
{}
{}
{
}
,,
ii
OOO
τ+= +FR RM RM, the torsor of the given and constraint internal
forces being equal to zero) and taking into account the properties of the triple scalar
product, we read
int int
int int
dd d d dd d d
RR RR
WWWW WWWW
′′ ′ ′
++ + =++ +
()d( )d
OOO
t
′
++ ⋅ + + ⋅RR r M M ω ,
(11.2.31)
finding thus the relation between the elementary work of the given and constraint forces
in the two frames: inertial and non-inertial. For the power of the given and constraint
forces we have
int int
int int
() ( )
RR RR OOO
PPPP PPPP
′′ ′ ′ ′
++ + =++ + ++⋅+ + ⋅RRv M M ω ,
(11.2.31')
so that we can state
11 Dynamics of Discrete Mechanical Systems
69
MECHANICAL SYSTEMS, CLASSICAL MODELS
Theorem 11.2.11 The power of the given and constraint external and internal forces
which act upon a discrete mechanical system, with respect to an inertial frame of
reference, is equal to the sum of the power of the same forces with respect to an
arbitrary non-inertial frame and the power of the given and constraint external forces
applied at the pole of the latter frame with respect to the inertial frame.
Let
{}
{
}
, 1,2,...,
i
in≡=VV and
{}
{
}
, 1,2,...,
j
jm
′′
≡=VV be two systems of
(bound or sliding) vectors of torsors, at the pole
O,
{}
{
}
,
OO
τ≡VRM and
{
}
{
}
,
OO
′′′
τ≡VRM
, respectively. We call torsor product (or comoment) of the two
torsors the scalar quantity
{}
{
}
()
,
OO
′′′
ττ =⋅+⋅VV RMRM
,
(11.2.32)
where
O is an arbitrary pole. Observing that the resultants R and
′
R
are invariant by a
change of pole and that
O
O
OO
′
′
=+×
J
JJJG
MM R
,
O
O
OO
′
′′′′
=+×
J
JJJG
MM R
, we can
write
()
,,
OO
OO
OO
′′
′′ ′ ′′′
⋅+⋅=⋅+ +⋅
J
JJJG
RM R M RM R R R M
()
,,
OO
OO
′′ ′ ′
+=⋅+⋅
J
JJJG
RRRMRM
;
hence, the comoment of two torsors does not depend on the pole with respect to which
it is calculated, the definition being thus consistent.
Introducing the kinematic torsor at the pole
O
{
}
,
OO
′
≡
′
vT ω ,
(11.2.33)
for which
O
O
OO
′
′′′
=+ ×
J
JJJG
vv ω
, we can write the relation (11.2.31') in the form
{
}
{
}
()
int int
int int
,
ii
RR RR
PP P P PP P P
′′ ′ ′
++ + =++ + + τ +τ
′
FRT
,
(11.2.31'')
where we have put in evidence the torsor of the given and constraint external forces.
Applying the theorem of kinetic energy with respect to an inertial frame of reference
and starting from (11.2.28), (11.2.28''), (11.2.31'), we can write
int
int
dd
dd
OO O C OC R R
TT
MMM PPPP
tt
′
′′ ′′ ′′ ′ ′ ′ ′
= − ⋅+ ⋅+ ⋅=++ +va av va
int
int
() ( )
RR OOO
PP P P
′
=+ + + + + ⋅ + + ⋅RRv M M ω ;
taking into account (11.2.14), (11.2.15) and (11.2.17), we get
()
int
int
d
,, ( ) ( )
d
OOC R ROO
T
MMPPPP
t
′′
++⋅=+++++⋅aav MMω
ρ
ω ,
(11.2.34)
70
where
d1
d2
OO
O
TT
tt t t
∂∂
∂
⎛⎞
=+⋅+⋅ +⋅
⎜⎟
∂∂∂
⎝⎠
KI
K
ωω ωω,
(11.2.34')
because
() ()
1111
2222
ij j i ij j i
OO
IIωω ωω⋅+⋅= +
IIωωωω
() ()
()
1
()
2
ij ji i j i j
OO
ij
II Iωω ωω=+ = =⋅ =⋅
IIωωωω.
A scalar product of the equation (11.2.18), (11.2.18') by
ω leads to
int
int
1
()
2
O
OOCRR
T
MPPPP
tt
∂
∂
⎛⎞
′
+⋅ − ⋅ + ⋅ = + + +
⎜⎟
∂∂
⎝⎠
I
Kavωωω
,
(11.2.34'')
where we have used the equation (11.2.34), (11.2.34').
The theorem of kinetic energy for the system of equations of motion (11.2.13) has
the form
() ()
int
int
11
nn
ii
ii
RR
t
C
ii
T
PP P P
t
==
∂
=++++⋅+⋅
∂
∑∑
Fv Fv;
(11.2.34''')
taking into account (11.2.13') and (11.2.18'') and observing that the last power vanishes,
we find again the relation (11.2.34'').
As V. Vâlcovici has shown, the theorem of kinetic energy with respect to an inertial
frame of reference maintains its form with respect to a non-inertial frame if and only if
1
()
2
O
OO C
M
t
∂
⎛⎞
′
⋅+⋅ =⋅
⎜⎟
∂
⎝⎠
I
Ka vωωω
.
(11.2.35)
If we have
= 0ω , hence TT= , then the non-inertial frame R does not rotate and
we obtain
22
11
() ()
22
OO C OO C
T T Mv M T Mv M
′′′ ′′′
=+ +⋅ =− +⋅vv vv
,
(11.2.36)
so that the theorem of kinetic energy takes the form
int
int
()
OC R R
T
MPPPP
t
∂
′
⋅+=+++
∂
av
.
(11.2.36')
From here (or from (11.2.35)) we deduce that the theorem of kinetic energy of a free
or constraint discrete mechanical system maintains its form with respect to a non-
inertial frame which does not rotate (
= 0ω ) if ()0
OC O C O
′′′′
⋅=⋅ − =av a v v
, hence
11 Dynamics of Discrete Mechanical Systems
71
