Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

′

, but reaches a position closer to that of stable equilibrium AB; after a certain

number of oscillations, the blade remains at rest). The consumption of energy due to

which it is impossible to increase the sum

TV+

(leading to a useful work) or, at least,

to let it remain constant (realizing a perpetuum mobile of the first species) can be

explained by the apparition of certain internal forces of friction and of certain external

resistant forces (e.g., the resistance of the air). Hence, not all internal forces are

conservative; non-conservative internal forces (e.g., forces of friction, which have a

sense opposite to that of the displacements, leading to a negative internal work) can be

put into evidence too. If the discrete mechanical system

S is adiabatically isolated (has

changes of energy with the exterior only if upon it is effected an external work), we are

led to the notion of internal energy,

int

, which results just from the work of non-

conservative internal forces and can depend on temperature, mass, volume etc. If upon

an adiabatically isolated discrete mechanical system no external work is exerted, then

we may write

int

d( ) d 0TV E++ =;

(11.1.47)

but if an external work is exerted too, then we can write, in general,

int

d( ) d dTV E W++ = .

(11.1.47')

An adiabatically non-isolated discrete mechanical system may receive energy from the

exterior, even if upon it no external work is exerted; but a flux of heat

dQ can

intervene. We may thus write

int

d( ) d d dTV E W Q++ = + .

(11.1.47'')

Introducing also an elementary work of non-mechanical and non-caloric nature

(e.g., of electromagnetic nature), we can write (after R.J. Mayer and J. Joule)

int

d( ) d d d dTV E W Q W++ = + + ;

(11.1.47''')

we obtain thus the first principle of thermodynamics. If

int

d0E = and the sum

dddWQW++ is an exact differential, we may state, after H. von Helmholtz, a

conservation theorem of energy of the form (11.1.46). One could thus say that it is

possible to realize a perpetuum mobile, where intervene transformations of kinetic,

potential and caloric energy or of other energies; but the experiment shows that the

caloric energy generated by frictions can be transformed in mechanical energy only by

loss of energy, the process being irreversible (one passes from mechanical energy to a

caloric one only by degradation).

11.1.2.8 Problem of n Particles

Let be an isolated (closed) free discrete mechanical system S, formed by n particles

of masses

m and position vectors

r , subjected only to the action of some internal

forces

ik ki

=−FF, ik≠ ,

, 1,2,...,ik n=

; if these forces are of Newtonian attraction

(or of Coulombian nature, of attraction or repulsion), then the corresponding problem is

known as the problem of

n particles. At a cosmic level, the celestial bodies can be

modelled, in a first approximation, as particles (e.g., the solar system, formed by the

Sun, the planets and their satellites, acted upon by other celestial bodies; their actions

are negligible external forces, due to the great distances at which these bodies are, as

well as due to their quasi-spherical distribution, their effects annulling each other). The

respective problem is called also the problem of

n bodies and is the basic problem in

celestial mechanics. At the atomic level, one has the same problem for the system

formed by nucleus and electrons.

The equations of motion read

∑



ik ik

=Fr,

ik k

=−rrr, , 1,2,...,ik n= ,

(11.1.48)

and lead to the vector first integrals

∑

HvC,

Mmt

′

==+

∑

rCCρ , ,const

′

JJJJG

(11.1.49)

which correspond to the conservation theorems of momentum and of rectilinear and

uniform motion of the centre of mass, respectively, to the vector first integral

ii i i i

=×= =

∑∑



Krr CΩ , const=

JJJJG

C ,

(11.1.49')

which corresponds to the conservation theorem of moment of momentum, and to the

scalar first integral

111

nnn

iik

TU mv f h

===

−= − =

∑∑∑

, consth = ,

(11.1.49'')

which corresponds to the conservation theorem of mechanical energy, where

ik k

PP=

JJJG

r , while f is the universal constant of attraction (we took into account

(1.1.84) and (3.2.6') for the forces of Newtonian attraction). We obtain thus ten scalar

first integrals for the 3n scalar differential equations of motion of second order. In 1887,

H. Burns showed that these first integrals are the only algebraic first integrals which can

be obtained; as well, in 1889, H. Poincaré stated that, besides these first integrals, one

cannot obtain other uniform and analytic first integrals, while Painlevé showed that

there does not exist other first integrals algebraic only with respect to the components

of the velocity vectors (neither for larger conditions). But, taking into account that time

does not appear explicitly in those first integrals, they are equivalent to 11 scalar first

integrals; moreover, observing that the internal forces depend only on the reciprocal

distances, one can obtain one more first integral. But there are necessary 6n scalar first

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

integrals to solve completely the problem, so that these 12 scalar first integrals are

sufficient only for

2n = .

We may write the n vector equations or the 3n scalar equations of motion,

respectively, in the form

ii i

mU=



r ∇ ,

()

∂

i∇

()

∂



, 1,2,...,in= , 1, 2, 3j = .

(11.1.48')

The centre of mass

C of an isolated discrete mechanical system S (e.g., the solar

system) has a uniform and rectilinear motion, so that remains to be studied its motion of

rotation about that centre.

Starting from the equations (11.1.48'), we get

() () ()

()

ii i

jj j

mx x x U

∂

==−

∂

∑∑



where we used Euler’s formula for a function

U, homogeneous of degree −1. Taking

into account the first integral (11.1.49'') too, we get

()

() () () () () () () ()

111

d1d

nnn

ii ii ii ii

iii

jj jj jj jj

iii

mxx xx mxx mxx U h

===

+= = =+

∑∑∑

    ;

one obtains thus the Lagrange-Jacobi formula (obtained by Lagrange in 1772 for

2n = and generalized by Jacobi in 1842 for any n)

2( 2 )

IUh=+



(11.1.50)

where

I is the polar moment of inertia of the discrete mechanical system S with

respect to the origin

Starting from the algebraic identity

() ( )

() () ( ) ()

11 1 11

22'

nn n nn

ii ki

ii i

jj jj

ki i ki

mmx mx mmx x

== = ==

⎛⎞

=+ −

⎜⎟

⎝⎠

∑∑ ∑ ∑∑

, 1, 2, 3j = ,

which can be easily verified, summing for

j from 1 to 3, introducing the mass M and

the moment of inertia

of the mechanical system S and taking into account the first

integral (11.1.28'''), it results

()

MI t R

′

=+ +CC

kik

Rmmr

∑∑

;

(11.1.50')

introducing in (11.1.50), we can write also the formula

()

RMUh

=− ,

(11.1.50'')

equivalent to the formula (11.1.50) and called the Lagrange-Jacobi formula too. If, in

particular,

OC≡ , then we have =C0, so that hh= . Integrating twice with respect

to time, we get

[]

2d ()2d

RRQTM U h

ττ τ=+ + +

∫∫

,constRQ=

(11.1.50''')

This last result allows to study the stability of the discrete mechanical system

S ;

after Jacobi, we say that this system is stable if the distances between the particles

remain finite, hence if

R is finite for t →∞. If there exists t so that tt∀> to have

2Uhε+>, 0ε > , then the discrete mechanical system S is labile; this takes place,

e.g., for

0h >

, because 0U > . We notice that one cannot have

2Uhε+<

, because

the second member of the relation (11.1.50''') would become negative for

t sufficiently

great. It results that, to ensure the stability of the discrete mechanical system

S it is

necessary that

0h <

and

2Uhε+<

for tt> .

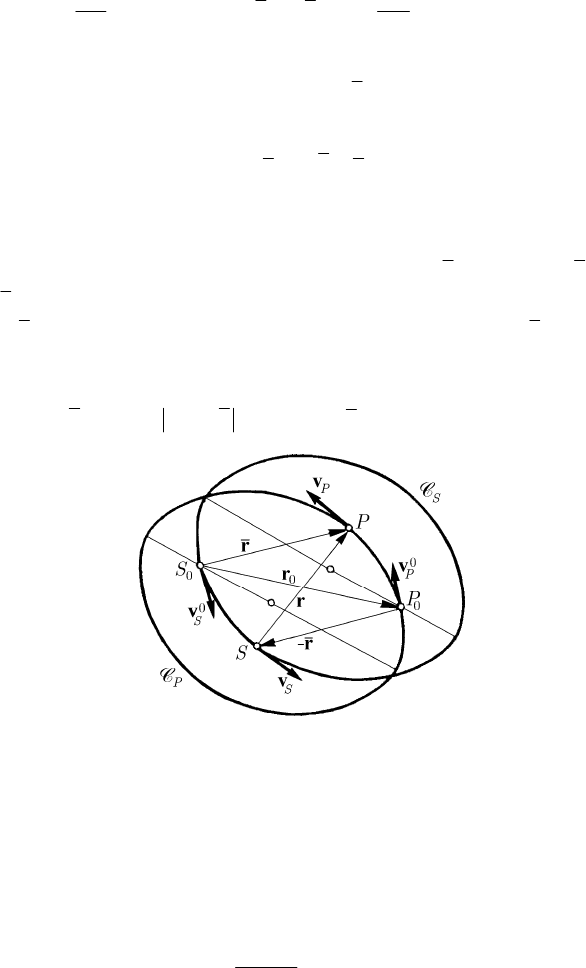
Fig. 11.5 Problem of two particles (the Sun and a planet)

The case

2n =

(the problem of two particles) has been considered in Chap. 8, Sect.

1.2.1, being reduced to the case of central forces (of attraction or of repulsion).

Assuming, e.g., that one of the particles is the Sun, of mass

M, the other particle being a

planet

P, of mass m, the equation of motion of a particle with respect to the other one

(for instance, the motion of the planet with respect to the Sun) reads (see the formula

(8.1.14))

=−



ru,

(11.1.51)

where

vers versSP==

ur (Fig. 11.5); hence, the motion of the particle P with

respect to the particle

S is identical (for analogous initial conditions) to the motion of a

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

particle

P, of mass m, attracted with a Newtonian force by the fixed centre S, of mass

Mm+

, and one can use the results obtained in Chap. 9, Sects. 2.1.2–2.1.4. The

Theorems 9.2.1 and 9.2.2 (the first two laws of Kepler) remain, further, valid. It results

that the particle

P moves with respect to the particle S along the ellipse, after the law

of areas, the particle

S being situated at one of the foci; concerning the motion of the

particle

S with respect to the particle P, one can make analogous statements. The

formula (9.2.17') allows to write

(

)

(

)

1/2

22121

() 2

aam am

Ta a a

Mm fM M fM M

ππ π

−

==+≅−

, (11.1.51')

where

a is the semi-major axis of the ellipse described by the particle P, T being the

period in which this ellipse is entirely travelled through; hence, it results

(

)

(

)

222 2

44 4

()

Tmm

Mm fM M fM M

ππ π

−

==+≅−

(11.1.51'')

Observing that, in case of the solar system, the ratio

m/M is negligible with respect to

unity (one obtains the greatest ratio

()

/10mM

−

= O for Jupiter, while for the Earth

we have

()

/10mM

−

= O ), we can admit the third law of Kepler too, with a good

approximation (as a matter of fact, the astronomical observations of Tycho Brahe are

thus explained). In case of binary stars, the relation (11.1.51') allows to deduce the sum

of the two masses

Mm+ , taking into account that the quantities a and T can be

measured by astronomical observations.

Let

−vv be the relative initial velocity of the particle P with respect to the

particle

S at the initial moment

t , where

and

are the initial velocities of the

particles

P and S, respectively. Taking into account the results in Chap. 9, Sect. 2.1.2,

it results that the trajectory of the particle

P is an ellipse if

()

2( )

rfMm−< +vv , a parabola if

()

2( )

rfMm−= +vv or a

hyperbola if

()

2( )

rfMm−> +vv , where

000

SP=

JJJJG

r is the position vector at

the initial moment; hence, the genus of the conic depends on the initial conditions.

Analogously, the motion of the particle

S with respect to the particle P takes place as

that particle would be attracted by the centre

P, the attractive mass being Mm+ ; the

genus of the conic

C described by the particle S is specified by the same conditions,

so that this particle describes a conic of the same genus as that of the conic

C ,

described by the particle

P. The two conics are both in the plane determined by the

vectors

r and

−vv, and are obtained one from the other by a plane translation;

hence, the axes of the two conics are parallel. If

P is a given position on

C , specified

In the case

3n = (the problem of three particles) one can no more obtain final

results in a finite form. If one of the particles,

S, has a mass M much greater than the

masses

m and

m of the other two particles

P and

P , respectively (e.g., the Sun

and two planets), then one can apply some methods of successive approximations.

Thus, one can consider, in a first approximation, the motion of the particles

S and

(as a problem of two particles). Further, one assumes that the particle

P perturbs the

Keplerian motion by the attraction exerted upon both particles

S and

P ; a perturbing

term which modifies the previous results is thus introduced. As a matter of fact, the

particle

perturbs the motion of the particle

too, introducing thus supplementary

In general, the problem of

n particles is decomposed in several problems

corresponding to

2n = or 3n = .

11.1.2.9 Discrete Mechanical Systems Subjected to Constraints

The discrete mechanical system

S of n particles

, of masses

m , and position

vectors

r , 1,2,...,in= , with respect to a fixed (inertial) frame of reference R,

previously considered, has 3n degrees of freedom, its position being specified by the

position of the representative point

()

PX in the representative space

E . If m

holonomic (rheonomic or scleronomic) ideal scalar constraints intervene, then the

equations of motion, the general theorems and, as a consequence, the conservation

theorems must be completed, introducing the constraint forces too. In general, we

assume that the mechanical system

S is subjected to 3mn< bilateral, holonomic

(finite, of geometric nature) constraints of the form (3.2.8); if we would have

3n distinct

constraints, the position of the representative point

P, hence of the mechanical system

S, would be specified from a geometric point of view (uniqueness or not). The case of

non-holonomic constraints of the form (3.2.13) will be studied later by analytical

11 Dynamics of Discrete Mechanical Systems

by the vector

SP=

JJJG

, we set up the vector

PS =−

JJG

, obtaining thus the cor-

responding position on

C . We notice also that the sense of motion of the particles

and is the same on the conics

C and

C , respectively. In case of the solar

system, both conics are ellipses, as we have assumed in Fig. 11.5.

terms. The iterative process of computation is convergent. The inverse problem can

be also put: to determine the position and the characteristics of a perturbing particle

if (by measurement or observations, eventually) the perturbations in the motion of

another particle are known. Thus, Leverrier discovered in 1845 the planet Neptune,

studying the perturbations of motion of the neighbouring planet Uranus; in recent

years (in 1961), from observations concerning the perturbations of the component A

of the binary star 61 of the constellation Swan, one has concluded that around this

component, at a distance of 11 light years, moves a planet greater than Jupiter, on

an elliptic trajectory. In 2005, a tenth planet of the solar system, at a greater

distance from the Sun than Pluto, seems to be discovered.

MECHANICAL SYSTEMS, CLASSICAL MODELS

methods. Returning to the representative point

P, the m bilateral holonomic constraints

specify that this point must be at the intersection of

m hypersurfaces (fixed or movable,

as the constraints are scleronomic or rheonomic, respectively) in the representative

space

E . In some cases, we can consider also unilateral constraints (the

representative point is at one side of a hypersurface).

Using the axiom of liberation from constraints and introducing the external

constraint forces

R (the resultant of the external constraint forces applied upon each

particle

P ) as well as the internal constraint forces

R , ik≠ , 1,2,...,kn= , the

equations of motion (11.1.8) read

()

ii i i

ik ik

=+ + +

∑



rFR F R

, 1,2,...,in= ;

(11.1.52)

in components, we can write

()

() () () ( ) ( )

iii ikik

jj j j j

mx F R F R

=++ +

∑

 , 1,2,...,in= , 1, 2, 3j = .

(11.1.52')

The position of the discrete mechanical system

S subjected to constraints can be

determined, at a given moment, by the equations (11.1.52') and by the constraint

relations, obtaining the functions

() ()

()

xxt= , 1,2,...,in= , 1, 2, 3j = ; in general,

we can state (as for

F and

F , see Sect. 11.1.1.3) that

()



RRrr,

()

ik ik l l



RRrr, ik≠ , , 1,2,...,ik n= , the motion of each particle depending

on the motion of all other particles. In this case, the mechanical system

S subjected to

constraints works as a free discrete mechanical system.

We notice that all the results obtained in the case of free discrete mechanical systems

can be transcribed for the discrete mechanical system

S subjected to constraints if we

add the constraint (unknown) forces to the given ones. In the first fundamental problem,

besides the trajectories (the vector functions

()

t=rr , 1,2,...,in= ), one must

determine also the constraint forces

R and

R , ik≠ , , 1,2,...,ik n= . In the

second fundamental problem, one must determine the forces

F ,

F and

R ,

R ; the

problem has not a unique solution. As well, nor in case of a mixed fundamental

problem the solution is unique.

In what concerns the theorems of existence and uniqueness, they remain further valid

if the functions (3.2.8) fulfil the conditions asked in Sect. 11.1.1.4 (are functions of

class

C and fulfil conditions of Lipschitz type).

Corresponding to the results in Sects. 11.1.2.1 and 11.1.2.2, we can write

()

=+=+

∑



HFRRR,

HRR=+



, 1, 2, 3j = ,

(11.1.53)

()

=+=+

∑



FR RRρ ,

MRRρ =+ , 1, 2, 3j = ,

(11.1.53')

()

iii

OOO

=×+=+

∑



KrFRMM,

Oj Oj Oj

KMM=+



1, 2, 3j =

(11.1.53'')

stating thus (the theorems take place in case of holonomic constraints, as well as in case

of non-holonomic ones; as well, we can assume to have unilateral constraints):

Theorem 11.1.21 (theorem of momentum). The derivative with respect to time of the

momentum of a discrete mechanical system subjected to constraints is equal to the

resultant of the given and constraint external forces which act upon this system.

Theorem 11.1.22 (theorem of motion of the centre of mass). The centre of mass of a

discrete mechanical system subjected to constraints moves as a free particle at which

would be concentrated the whole mass of this system and which would be acted upon by

the resultant of the given and constraint external forces.

Theorem 11.1.23 (theorem of moment of momentum). The derivative with respect to

time of the moment of momentum of a discrete mechanical system subjected to

constraints, with respect to a fixed pole, is equal to the resultant moment of the given

and constraint external forces which act upon this system, with respect to the same

pole.

Introducing the areal accelerations as well as the notion of hodograph, we can state

theorems analogous to Theorems 11.1.8', 11.1.5' and 11.1.8'', respectively.

Observing that

{

}

{

}

{

}

ii i

OOO

τ=τ+τ



HFR,

(11.1.53''')

we may state

Theorem 11.1.24 (theorem of torsor). The derivative with respect to time of the torsor

of momenta of a discrete mechanical system subjected to constraints, with respect to a

fixed pole, is equal to the torsor of the given and constraint external forces which act

upon this system, with respect to the same pole.

Introducing the impulse of the resultant of the external constraint forces

∑

∫

and the impulse of the resultant moment of the external constraint forces

∑

∫

rR , corresponding to the time interval

[

]

,tt , we can write (the internal

constraint forces do not intervene in computation)

222

111

()d d d

ttt

Δ= + = +

∑

∫∫∫

HFR RR,

(11.1.54)

222

111

()d d d

ttt

iii

OOO

ttt

Δ= ×+ = +

∑

∫∫∫

KrFRMM

(11.1.54')

{}

{

}

{

}

ii i

OO O

ttΔτ = τ + τ

∫∫

HF R

(11.1.54'')

The relation (11.1.24) is completed in the form

int

dd d d d

TWW W W=+ + +

(11.1.55)

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

and we can state

Theorem 11.1.25 (theorem of kinetic energy). The differential of the kinetic energy of a

discrete mechanical system subjected to constraints is equal to the elementary work of

the given and constraint external and internal forces which act upon this system.

As it was shown in Chap. 3, Sect. 2.2.9, in case of scleronomic constraints (or even

in a more general case, that is in case of catastatic constraints) we have

int

dd 0

WW==

; in this case, the Theorem 11.1.25, corresponding to a discrete

mechanical system subjected to constraints, is stated in the same form as the Theorem

11.1.10, corresponding to a free mechanical system. In what concerns the Theorems

11.1.10' and 11.1.10'', one can make analogous observations.

As well, if the moment of momentum is written with respect to a pole

Q, movable

with respect to the fixed origin

O, the formula (11.1.23') leads to

{} {} {}

{

}

ii i

QQQ Q

τ=τ+τ−×



HFR0vH.

(11.1.56)

Using the results given in Sects. 1.2.5–1.2.7, we may set up first integrals, in certain

conditions, in case of a discrete mechanical system subjected to constraints too. Thus, if

the sum

+RR is parallel to a fixed plane (is normal to a fixed direction of unit vector

()

0+⋅=RRu ), then we can write the first integral (11.1.28); analogously, if the

sum

+MM

is contained in a fixed plane (is normal to a fixed axis Δ, O Δ∈ , of

unit vector

()

+⋅=MMu ), then one obtains the first integral (11.1.31).

+=RR 0 (necessary condition of static equilibrium), then we can state a

conservation theorem of momentum and a theorem of rectilinear and uniform motion of

the mass centre, while if

+=MM 0 (necessary condition of static equilibrium),

then we may state a conservation theorem of moment of momentum. If both conditions

are fulfilled simultaneously (necessary and sufficient conditions of static equilibrium in

case of a non-deformable mechanical system), then one can state a conservation

theorem of torsor.

In case of scleronomic (or even catastatic) constraints and of conservative internal

forces, we can state a theorem of mechanical energy in the form of Theorems 11.1.19–

11.1.19'', and if

d0W = too, for a certain interval of time, we obtain a conservation

theorem of mechanical energy, stated as the Theorem 11.1.20.

We mention that the conservation theorem of moment of momentum allows to state

in this case a theorem of areal velocities, and a theorem of areas too.

As in case of a free discrete mechanical system, one can obtain only

6n independent

first integrals; but these ones are sufficient to determine the motion. Even if the

constraint forces are not known a priori, the conditions imposed above are sometimes

fulfilled, so that one can build up first integrals also in case of discrete mechanical

systems subjected to constraints.

In case of constraints with friction one can make considerations analogous to those

in case of the motion of a single particle (see Chap. 6, Sect. 2.2.3).

11.1.2.10 Differential Principles of Mechanics

The equations of motion of a discrete mechanical system, free or subjected to

constraints, are written in the form (11.1.8) or in the form (11.1.52), respectively; these

equations correspond to the second principle of Newton, the first differential principle

of mechanics. As in the case of a single particle, this basic principle can be expressed

also in other equivalent forms, which are useful in various particular cases; if they are

considered as consequences of Newton’s principle, these equivalent forms are

theorems.

Introducing the forces of inertia

iii

m=−



Fr, 1,2,...,in= ,

(11.1.57)

the law of motion reads (we consider the more general case of a discrete mechanical

system subjected to constraints)

'( )

ii i

ik ik

++ + + =

∑

FFR F R 0, 1,2,...,in= ,

(11.1.58)

and we can state

Theorem 11.1.26 (d’Alembert). The motion of a discrete mechanical system subjected

to constraints takes place so that, at any moment, it is in dynamic equilibrium under the

action of the given and constraint, external and internal forces which act upon it and of

the forces of inertia.

Obviously, each particle (more general, each subsystem) of the system is in dynamic

equilibrium.

We introduce the forces

iii i ii

ik ik

=++ =+ −

∑∑



FF F F F rΦ , 1,2,...,in= ,

(11.1.59)

which are called the lost forces of d’Alembert; the equations (11.1.58) become, in this

case,

++ =

∑

RR0Φ , 1,2,...,in= ,

(11.1.60)

and we may state

Theorem 11.1.26' (d’Alembert). The motion of a discrete mechanical system subjected

to constraints takes place so that, at any moment, the constraint external and internal

forces are in equilibrium with the lost forces of d’Alembert.

This equilibrium takes place for each particle, hence for any subsystem of the

considered mechanical system. We can thus state:

Theorem 11.1.27 (theorem of dynamic equilibrium of parts). If a discrete mechanical

system

S subjected to constraints is, at a given moment, in dynamic equilibrium under

the action of the lost forces of d’Alembert and of the constraint external and internal

forces which act upon it, then any part of the system (any subsystem

S ⊂ S ) will be in

11 Dynamics of Discrete Mechanical Systems