Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

() () d d

tt t t

Δ− =

∑

∫∫

HH H F R;

(11.1.18')

the variation of the momentum of a free discrete mechanical system in a finite interval

of time is thus put into evidence. The quantity

∫

R represents the impulse of the

resultant of the given external forces, corresponding to the interval of time

[

]

,tt .

The notion of hodograph, introduced in Chap. 5, Sect. 1.2.1, leads to a kinematical

interpretation of the Theorem 11.1.5; we state thus

Theorem 11.1.5' The velocity of a point which describes the hodograph of the

momentum of a free discrete mechanical system with respect to a fixed pole is

equipollent to the resultant of the given external forces which act upon this system.

11.1.2.2 Theorem of Moment of Momentum

We perform a vector product at the left of each equation of motion (11.1.8) by

r and

sum for all particles of the mechanical system

S ; taking into account the relation

(2.2.50) which is verified by the internal forces, we obtain

ii i i i

×= ×

∑∑



rr rF,

where the internal forces disappear. Introducing the momentum

H and the moment of

momentum

K , we notice that

()()()

ii i i i i i i i i i i i

mm m

×= ×+×= ×= × =



  

rr rrrr rr rH K

so that we may write

==×=

∑



KrFM

() ()

Oj jkl Oj

KxM

= ∈ =

∑



1, 2, 3j =

(11.1.20)

Thus, we state

Theorem 11.1.8 (theorem of moment of momentum). The derivative with respect to time

of the moment of momentum of a free discrete mechanical system, with respect to a

fixed pole, is equal to the resultant moment of the given external forces which act upon

this system, with respect to the same pole.

In this theorem, the derivative



as well as the resultant moment of the given

external forces are bound vectors, applied at the pole

O. As well, the first relation

(11.1.20) remains valid if it is projected on a plane or on an axis (the second group of

relations (11.1.20)). We may also write

∑



Ω ,

() () ()

iii

kl Oj

Oj k l

mmxxMΩ

= ∈ =

∑∑





, 1, 2, 3j = , (11.1.20')

putting thus into evidence the areal accelerations of the component particles of the

mechanical system

S ; we can state

Theorem 11.1.8' (theorem of areal accelerations). The sum of the products of the

double masses of the particles of a free discrete mechanical system by their areal

accelerations, with respect to a given fixed pole, is equal to the resultant moment of the

given external forces which act upon this system with respect to the same pole.

Another form of the relation (11.1.20) is given by

() () d d

OO O O

tt t t

Δ− ×=

∑

∫∫

KK K rF M;

(11.1.20'')

thus, the variation of the moment of momentum of a free discrete mechanical system, in

a finite interval of time, is put into evidence. The quantity

∫

M represents the

impulse of the resultant moment of the given forces with respect to the pole

corresponding to the interval of time

[

]

,tt .

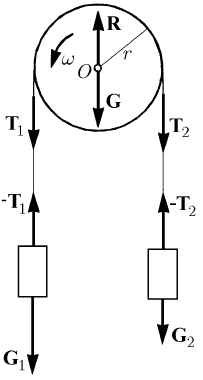
Fig. 11.1 The Atwood engine

With the aid of the hodograph too, the kinematic form of the theorem of moment of

momentum is expressed by (for the sake of simplicity, we choose the pole of the

moment of momentum as pole of the hodograph)

Theorem 11.1.8'' The velocity of the point which describes the hodograph of the

moment of momentum of a free discrete mechanical system with respect to a given fixed

pole is equipollent to the resultant moment of the given external forces which act upon

this system, with respect to the same pole.

We will use these results in the study of the Atwood engine, which allows to verify

the law of falling of the bodies. This engine is formed by a wheel of radius

r and weight

G, which is rotating frictionless, with the angular velocity ω, about a horizontal axle,

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

which passes through the pole

O; over the wheel passes frictionless an inextensible and

perfect flexible and torsionable thread, at the ends of which are suspended the weights

m=Gg

mm> (Fig. 11.1); we assume that the mechanical system

is moving with the velocity

vv v rω=== . The theorem of moment of momentum

is written in the form

11 22 1 2

()

Imvrmvrmgrmgr

ω ++ =−,

where

I is the polar moment of inertia of the wheel with respect to the pole O; in this

case, the acceleration

av=



is given by

−

′

mmm

′

=++

(11.1.21)

where

′

is the reduced mass of the mechanical system. We notice that ag< ; if the

difference

mm− is small, then we have ag . Thus, we obtain easy the

acceleration

a, in the frame of an experiment; the acceleration g is then given by the

formula (11.1.21) (

mmI

and r are known quantities). The tensions

and

the thread and the constraint force

R are then easily obtained

11 21

() ( )

Tmga mmmg

′

=−= +−

′

22 12

() ( )

Tmga mmmg

′

=+= +−

′

(11.1.21')

12 12 21

()() ( )

RmmgmmaG mmmgG

−

′

=+ −− += +− +

′

The theorem of moment of momentum with respect to the pole

O, written only for

the subsystem formed by the wheel (

()

ITTrω =−



), may be used to verify the

results obtained above.

11.1.2.3 Theorem of Torsor

Starting from (11.1.4), we notice that

{}

{

}

τ=





HHK; but

∑



HHH,

()

11 1

nn n

ii iiii ii

ii i

== =

=×=×+×=×

∑∑ ∑





KrHrHrHrH

so that

{}

{

}

τ=τ



HH. Because

{

}

{

}

τ=FRM, starting from (11.1.18)

and (11.1.20), we get

{} {} {}

iii

OOO

τ=τ=τ



HHF,

(11.1.22)

stating thus

Theorem 11.1.9 (theorem of torsor). The derivative with respect to time of the torsor of

momenta of a free discrete mechanical system with respect to a given fixed pole is equal

to the torsor of the given external forces which act upon this system, with respect to the

same pole.

Thus, by introducing the notion of torsor, we get a synthesis of the theorems of linear

and angular momenta, which has the advantage to contain only the given external

forces (the internal forces are eliminated). The theorem of torsor implies two vector

relations or six scalar relations.

The variation of the torsor of momenta of a free discrete mechanical system with

respect to a given fixed pole, in an interval of time

[

]

,tt , is obtained in the form

{} {} {}

{

}

ii i i

OO O O

tt tt

Δτ τ − τ τ

∫

HH H F==

(11.1.22')

This relation plays an important rôle in case of a small interval of time and, especially,

in case of discontinuous phenomena.

The general theorems stated above take place with respect to an inertial frame of

reference

R, considered as fixed; the theorem of moment of momentum and the

theorem of torsor, which depend on the pole

O, maintain their form with respect to

another pole

Q, rigidly connected to the frame R (fixed with respect to this frame). If

the pole

Q is movable, calculating further with respect to the frame R, the momentum

remains invariant, but (as in Chap. 6, Sect. 1.2.4) the moment of momentum and the

resultant moment of the given external forces become

OQQ

=+×KKrH,

OQQ

=+×MMrR,

OQ=

JJG

;

replacing in (11.1.20) and taking into account (11.1.18), we may write (

QP=

JJG

)

QQQQ

==×−×=−×

∑



KrFvHMvH

(11.1.23)

obtaining thus a generalized form of the theorem of moment of momentum. The

formula (11.1.22) is generalized in the form

{} {} {}

{}

iii

QQQQ

τ=τ=τ−×



HHF0vH

(11.1.23')

11.1.2.4 Theorem of Kinetic Energy

We perform a scalar product of each equation of motion (11.1.8) by

r and sum for all

the particles of the mechanical system

S, and obtain

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

1111

dd'd

nnnn

ii i i i i

iiik

====

⋅= ⋅+ ⋅

∑∑∑∑



rr Fr F r

;

observing that

dddd

iiii ii iiii

mmmm

⋅= ⋅= ⋅= ⋅



   

rrrrrr

d( )



d( ) d

ii i

mv T==

and taking into account (3.2.3), (3.2.4) and (11.1.6'), we may write

int

dd dTWW=+ , (11.1.24)

stating thus

Theorem 11.1.10 (theorem of kinetic energy; Daniel Bernoulli). The differential of the

kinetic energy of a free discrete mechanical system is equal to the elementary work of

the given external and internal forces which act upon this system.

Unlike the theorem of torsor, in the theorem of kinetic energy intervene also the

internal forces in calculation. Dividing the relation (11.1.24) by

dt and taking into

account (11.1.7), (11.1.7'), we can write this theorem in the form (closer to the previous

ones)

int

TPP

==+



(11.1.24')

obtaining thus

Theorem 11.1.10' (theorem of kinetic energy; second form). The derivative with

respect to time of the kinetic energy of a free discrete mechanical system is equal to the

power of the given external and internal forces which act upon this system.

In general, the elementary work is not an exact differential (it is a Pfaff form); the

theorem of kinetic energy may be written in the form (for

[

]

,ttt∈ , between the

positions

P and

P of the representative point P in the space

E )

12 12

2121

int

() ()

PP PP

TTt Tt T T W WΔ= − = − = +

12 12

111

d'd

nnn

ii i

PP PP

iik

===

=⋅+ ⋅

∑∑∑

∫∫

Fr F r

2222

1111

int

111

d' dd d

nnn

tttt

ii i

tttt

iik

ttPtPt

===

=⋅+ ⋅=+

∑∑∑

∫∫∫∫

Fv F v

(11.1.24'')

and we can state

Theorem 11.1.10'' (theorem of kinetic energy; finite form). The variation of the kinetic

energy of a free discrete mechanical system in a finite interval of time is equal to the

work effected by the external and internal forces which act upon this system in the

considered interval of time.

If we write the relation (11.1.18') for only one particle

P (we must introduce also

the influence of the internal forces) and if we perform a scalar product by the velocity

(2)

v at the finite moment (the velocity

(1)

v takes place at the initial moment), and if

we sum for all the particles of the discrete mechanical system

S, then we obtain

()

(2) (1) (2) (2)

11 1 1

nn n n

ii i

iiii

ii i k

mv m t

== = =

⎛⎞

−⋅=⋅+

⎜⎟

⎝⎠

∑∑ ∑ ∑

∫

vv v F F ;

introducing the notations

()

(1)

Tmv

∑

()

(2)

Tmv

∑

()

(0)

Tmv

∑

(11.1.25)

where

T is the kinetic energy of the lost velocities, while

(0) (2) (1)

iii

=−vvv, it results

(2)

TT t

⎛⎞

Δ+ = ⋅ +

⎜⎟

⎝⎠

∑∑

∫

vFF

(11.1.26)

and we can state

Theorem 11.1.11 The sum of the variation of the kinetic energy of a free discrete

mechanical system in a finite interval of time and the kinetic energy of the lost velocities

in the same interval of time is equal to the sum of the scalar products of the impulses of

the given external and internal forces which act upon this system, corresponding to the

considered interval of time, by the velocities of the particles at the final moment.

Analogously, we find (we perform a scalar product by the velocities

(1)

v and sum

for all the particles of the mechanical system

S )

(1)

TT t

⎛⎞

Δ− = ⋅ +

⎜⎟

⎝⎠

∑∑

∫

vFF

(11.1.26')

and state

Theorem 11.1.11' The difference between the variation of the kinetic energy of a free

discrete mechanical system in a finite interval of time and the kinetic energy of the lost

velocities in the same interval of time is equal to the sum of the scalar products of the

impulses of the given external and internal forces which act upon this system,

corresponding to the considered interval of time, by the velocities of the particles at the

initial moment.

Summing the relations (11.1.26) and (11.1.26') and taking into account the relation

(11.1.24''), we get

()

12 12

(1) (2)

int

PP PP

TW W t

⎛⎞

Δ= + = + ⋅ +

⎜⎟

⎝⎠

∑∑

∫

vv F F ;

(11.1.27)

thus, we state

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

Theorem 11.1.12 (Kelvin). The work effected by the given external and internal forces

which act upon a free discrete mechanical system in a finite interval of time (the

variation of the kinetic energy of the respective mechanical system) is equal to the sum

of the scalar products of the impulses of the given external and internal forces which

act upon this system, corresponding to the considered interval of time, by the semi-sum

of the velocities of the particles at the initial and final moments.

Subtracting the relation (11.1.26') from the relation (11.1.26), we may write

(0)

⎛⎞

=⋅+

⎜⎟

⎝⎠

∑∑

∫

vFF;

(11.1.27')

there results

Theorem 11.1.12' (analogue to Kelvin’s theorem). The kinetic energy of the lost

velocities of a free discrete mechanical system in a finite interval of time is equal to half

of the sum of the scalar products of the impulses of the given external and internal

forces, which act upon this system, corresponding to the considered interval of time, by

the lost velocities, in the same interval of time.

If the given external and internal forces which act upon a free discrete mechanical

system

S satisfy certain conditions, then the general theorems stated above lead to

conservation theorems (hence, to first integrals of the system of differential equations of

motion). Thus, if the resultant

R of the given external forces is parallel to a fixed plane

(is normal to a fixed direction of unit vector

u, with respect to the frame R , or has a

zero component,

0⋅=Ru ), as in the case of a single particle (see Chap. 6, Sect.

1.2.5), then the theorem of momentum allows to write

() ()

111

nnn

ii j j i

iii

muHumvC

===

⋅=⋅ = = =

∑∑∑

Hu u v , constC = ;

(11.1.28)

we obtain thus a scalar first integral. Hence, if the resultant

R of the given external

forces is parallel to a fixed plane, then the projection of the momentum of the free

discrete mechanical system

S on the normal to this plane is conserved (is constant) in

time. Because

11 1

nn n

i i ii ii

ii i

mm mC

== =

⎛⎞

⋅=⋅=⋅ =

⎜⎟

⎝⎠

∑∑ ∑



uvur ur

it results

()

ii j i

mumxCtC

′

⋅= =+

∑∑

ur , ,constCC

′

= ,

(11.1.28')

obtaining a new scalar first integral, independent of the previous one; thus, the

mentioned condition allows to build up two independent scalar first integrals.

11.1.2.5 Conservation Theorems of Momentum. Applications

Analogously, if the resultant

R has a fixed direction (is normal to two non-parallel

fixed directions with respect to the frame

R or has two zero components), then we

obtain four independent scalar first integrals of the form (11.1.28), (11.1.28'), while the

projection of the momentum of the free discrete mechanical system

S on a plane

normal to the resultant

R (determined by the two fixed directions) is conserved in time.

Finally, if the resultant

R of the given external forces vanishes (is normal to three

distinct fixed directions), then we may set up three independent scalar first integrals of

the form (11.1.28). As a matter of fact,

=R0 leads to =



H0 and to

∑

HvC, const=

JJJJG

C ,

HC= , 1, 2, 3i = ,

(11.1.28'')

hence to a vector first integral, equivalent to three scalar first integrals; we state thus

(we take into account (11.1.19) too)

Theorem 11.1.13 (conservation theorem of momentum). The momentum (and the

velocity of the centre of mass) of a free discrete mechanical system is conserved in time

if and only if the resultant of the given external forces which act upon it vanishes.

Starting from (11.1.19), we can write

′

=+CC

,const

′

JJJJG

ii i

MCtCρ

′

1, 2, 3i =

;

(11.1.28''')

thus, we get a new vector first integral, equivalent to three scalar first integrals, and we

may state

Theorem 11.1.14 (theorem of rectilinear and uniform motion of the centre of mass).

The motion of the centre of mass of a free discrete mechanical system is rectilinear and

uniform if and only if the resultant of the given external forces which act upon this

system vanishes.

Observing that the Theorem 11.1.14 is a consequence of the Theorem 11.1.13 (and

inversely), it results that the conservation theorem of momentum allows to set up two

vector first integrals or six scalar first integrals (the maximal number of independent

scalar first integrals which can be obtained).

Returning to the Theorem 11.1.7 of general motion of the centre of mass of a free

discrete mechanical system, we can mention many applications. Let thus be a discrete

mechanical system

S of free particles launched in vacuum and subjected only to the

action of a uniform gravitational field; no matter the internal forces could be, the centre

of mass

C of the mechanical system S (considered as a particle acted upon by the

resultant of the gravity forces) describes an arc of parabola of vertical axis. For

instance, if a projectile launched in the vicinity of the Earth explodes at a certain

moment, then the particles thus obtained (various parts of the projectile) are moving so

that the instantaneous centre of mass of the system thus formed describes, further, the

same parabola; indeed, the forces which are developed by explosion are internal ones

and do not intervene in calculation. If, at a certain moment, intervene also other external

forces (e.g., the collision of a part of the projectile with the ground or other bodies),

then the trajectory of the centre of mass is modified.

We have seen that, in the absence of external forces, the centre of mass has a

rectilinear and uniform motion; this result has been verified by many astronomical

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

observations. Indeed, assuming that the solar system is isolated (it is not acted upon by

external forces, which can be practically accepted, because the other stars and their

planets are at great distances from the solar system, so that their influence may be

neglected), its centre of mass (very close to the centre of mass of the Sun) has a

rectilinear motion, with a velocity of

19.5 km/s, towards a point called Apex, in the

vicinity of the star Vega of the constellation Lyra.

If, in the above case, the initial velocity of the centre of mass is zero with respect to

an inertial frame of reference

R, then the centre of mass is at rest with respect to this

frame at any moment. Assuming that the theorem of motion of the centre of mass can

be applied also in case of continuous mechanical systems (as it will be seen in Sect.

12.1.2.1), we will apply the above results to living matter too. The will of living beings

puts in action their muscles; these actions are internal forces, which do not intervene in

computation, so that a living being can change the rectilinear and uniform motion (or

the rest) of its centre of mass only by acting upon some external mechanical systems

(bodies). Thus, a man which stays on a perfect smooth horizontal plane cannot advance

(cannot “go”); indeed, the external forces which act upon the human body are vertical,

so that its centre of mass can move only along the vertical (there exist no horizontal

components). The going becomes possible only because, in reality, the ground (plane

surface) cannot be perfect smooth, a sliding friction taking, practically, place. In this

case, the man, immobile at the beginning, raises a foot and advances one step; the other

foot, in contact with the ground, tends to make a motion in an opposite direction, not to

have a horizontal component of motion of the mass centre. At this moment appears an

oblique reaction of the ground, with a horizontal component due to friction, directed

towards forward; this reaction transported parallel to itself at the centre of mass,

determines a forward motion.

Let us consider the case of a non-deformable mechanical system

S of mass M,

which has a motion of translation of velocity

v with respect to a fixed frame of

reference

R, and a particle P of mass m, which moves with a velocity u with respect to

the mechanical system

S, hence with a velocity

′

vvu with respect to the frame

R ; we assume that the resultant of the external forces which act upon the mechanical

system

{}

P=∪

′

vanishes. The conservation theorem of momentum allows to

write

()Mm Mm m

′

+=+ +=vv vuC, const=

JJJJG

C ;

(11.1.29)

if the mechanical system

′

S is at rest with respect to the frame R at the initial

moment

t (

() ()tt

′

==vv 0, hence

()t =u0), then we get =C0, so that

=−

(11.1.29')

Hence, if the particle

P begins to move with the velocity u with respect to the non-

deformable system

S, then a velocity v of opposite direction is conveyed to the latter

one; supposing that

mM (hence /( ) /mM m mM+≅ ), it results vu.

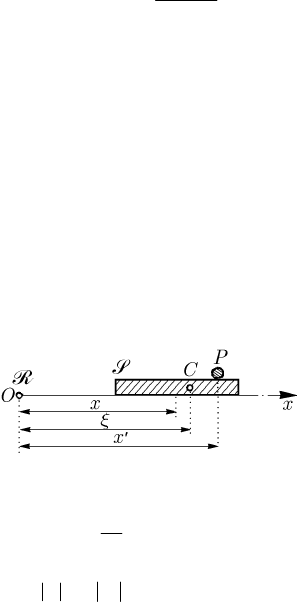
The motion being rectilinear, in this case, we can consider that it takes place along the

Ox-axis, the mass centre of the mechanical system S (materialized by a rigid straight

bar, Fig. 11.2) having the abscissa

()xt and the velocity ()vt , while the particle P is

of abscissa

()xt

′

and velocity () () ()vt vt ut

′

=+ ( ()ut is the velocity with respect

to the mechanical system

S ); we may thus write

0Mv mv

′

+=,

=−

(11.1.30)

Integrating with respect to time (which corresponds to the Theorem 11.1.14), it results

()constMx mx Mx mx M m ξ

′′

+= + =+ =

(11.1.30')

where

()xxt= ,

()xxt

′′

= , while

() ( ) constttξξ== is the abscissa of the

mass centre

C of the mechanical system

′

S (Fig. 11.2), which remains at rest with

respect to the frame

R. Denoting by

xxδ =− ,

xxδ

′′′

=−

the displacements of

the mechanical system

S and of the particle P, respectively, positive in the positive

sense of the

Ox-axis, we obtain the displacement of the mechanical system S as a

function of the displacement of the particle

P (of an opposite direction to the latter one)

Fig. 11.2 Motion of translation of a mechanical system

δδ

′

=−

;

(11.1.30'')

because

mM , it results δδ

′

 too. These results explain why the centre of

mass of the system formed by a boat (on a non-running water) and by a man is not

displacing, no matter the action of the man upon the boat (if the man moves in a

direction, then the boat moves in the opposite one); if the boat is near to the border and

the man advances in it towards the border, trying to go down, then the boat moves away

from the border. Analogously, the repulsion of a gun at the moment of the discharge is

thus explained; the velocity of this repulsion is given by the second formula (11.1.30)

as a function of the initial velocity of the projectile (bullet), while the formula

(11.1.30'') gives the displacement back of the gun (of its mass centre) as a function of

the distance travelled through by the projectile along its barrel (during the time in which

the gun

S and the projectile P form a mechanical system

′

S ).

11 Dynamics of Discrete Mechanical Systems