Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

Analogously, the kinetic energy is given by

()

222

11 1 1 1

11 1 1

22 2 2

nn n n n

ii i i ii ii i

ii i i i

Tmv m mr m m

== = = =

′′ ′ ′ ′

==+=+⋅+

∑∑ ∑ ∑ ∑

   

rr

ρρρ,

so that we may write

() 2

TT M

′′



(11.2.4)

()C

T being the kinetic energy of the system in relative motion (with respect to the mass

centre); we thus state

Theorem 11.2.2 (S. Koenig). The kinetic energy of a discrete mechanical system with

respect to a fixed frame of reference is equal to the sum of the kinetic energy of the

same system with respect to a Koenig frame of reference and the kinetic energy of the

mass centre at which the whole mass of the mechanical system is concentrated, with

respect to the fixed frame.

The elementary work of the given and constraint, external and internal forces is

given by

int

111

dd d d ( )d '( )d

nnn

ii i i

R R ik ik

iik

WW W W

===

′′ ′ ′ ′ ′

+++ =+⋅+ +⋅

∑∑∑

FR r F R r

111

()(dd) '( )(dd)

nnn

ii i i

ik ik

iik

===

′′

= +⋅+ + + ⋅+

∑∑∑

FR r F R r

ρρ

;

hence,

() () ()

()

int

dddddddd()d

CCC

WWWW WWWW

′′ ′ ′ ′

+++=+++++⋅RR

(11.2.5)

and we can state (we denote by upper index the elementary work with respect to a

Koenig frame of reference)

Theorem 11.2.3 (of Koenig type). The elementary work of the given and constraint,

external and internal forces which act upon a discrete mechanical system, with respect

to a fixed frame of reference, is equal to the sum of the elementary work of the same

forces, with respect to a Koenig frame, and the elementary work of the given and

constraint external forces, considered to be applied at the mass centre, with respect to

the fixed frame.

From (11.2.5) we notice that we can write

()

dd d

WW t

′′

=+⋅Rv

()

dd d

WW t

′′

=+⋅Rv

()

int

′

()

int

′

= .

(11.2.5')

Hence, the elementary work of the external (given and constraint) forces is not the same

with respect to an inertial (fixed) frame of reference and to a non-inertial (movable)

Koenig frame, its variation depending on the resultant of the external (given and

constraint) forces; this elementary work (e.g., of the given external forces) remains

invariant if and only if the scalar product

′

⋅=

Rv , hence if the resultant =R0 or

′

v0 (the centre of mass is rigidly linked – at rest – with respect to the fixed

frame) or if

′

⊥

vR (the resultant of the given external forces is contained, at any

moment, in a plane normal to the trajectory of the centre of mass). In case of catastatic

external constraints, the elementary work of the constraint external forces with respect

to an inertial frame (in the absolute motion) vanishes (

′

= ); from (11.2.5') it

results that the elementary work with respect to a non-inertial Koenig frame (in the

relative motion) is, in general, non-zero. This elementary work remains invariant only if

′

⋅=

Rv (which has an analogous mechanical interpretation as above). In exchange,

the elementary work of the internal forces (for which the resultant vanishes) remains

always invariant by passing from an inertial frame to a non-inertial Koenig frame.

We notice that the Theorem 3.1.4 (Huygens-Steiner) is of the same type as Koenig’s

theorems. As well, the formulae (3.1.9) and (11.2.2) are of the same type, the

corresponding quantities being equal to zero with respect to a Koenig frame.

11.2.1.2 General Theorems with Respect to a Koenig Frame. Conservation Theorems

Passing from a given frame of reference

′

R to a Koenig frame R, the sum of the

given and constraint external forces

()

′′

+= + =+

∑

RR FR RR

(11.2.6)

remains invariant; assuming that the frame

′

R is inertial and using the formula

(11.2.2), the Theorem 11.1.21 of the momentum allows to find again the Theorem

11.1.22 of motion of the centre of mass.

As well, the resultant moment of the given and constraint external forces is

expressed in the form

()()()

iii i ii

′′

′′ ′ ′

+ = ×+ = +×+

∑∑

MM rFR r FRρ

() ()

iii ii

′

=×++× +

∑∑

rFR FRρ ,

so that

()

′′

′′ ′

+=++× +

∑

MM MM FRρ ,

(11.2.6')

hence a formula of the form (2.2.27) (a result of the same form as the theorems of

Koenig type). In this case, assuming – further – that the frame

′

R is inertial and

taking into account the Theorem 11.2.1, the Theorem 11.1.23 of the moment of

momentum leads to (without distinction between the absolute and the relative

derivatives, because

= 0ω )

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

() () ( )

′

′′′′′ ′

=+× +× =++× +

∑



 

KK MM FRρρρρ ρ ;

using the theorem of motion of the centre of mass, we obtain, finally,

()C



KMM

(11.2.7)

so that we state

Theorem 11.2.4 (S. Koenig). The theorem of moment of momentum remains invariant

by passing from an inertial (fixed) frame of reference to a non-inertial (movable)

Koenig frame.

Taking into account the Theorems 11.2.2 and 11.2.3 and assuming that the frame

′

R is inertial, the Theorem 11.1.25 of the kinetic energy allows to write (we have, as

well,

() ()

d/d /

TtTt=∂ ∂ ; an upper index specifies the kinetic energy with

respect to a Koenig frame)

() ()

dd dd d

TT M T M

′′′′′

=+⋅ +⋅

 

ρρ

() () ()

()

int

dddd ()d

CCC

WWWW

⎡⎤

′

=+++++⋅

⎢⎥

⎣⎦

∑

so that (we use, further, the theorem of motion of the centre of mass)

() () ()

() ()

int

ddddd

CCC

TWWWW=+++,

(11.2.8)

and we can state

Theorem 11.2.5 (S. Koenig). The theorem of kinetic energy remains invariant by

passing from an inertial (fixed) frame of reference to a non-inertial (movable) Koenig

frame.

The Theorems 11.2.4 and 11.2.5 represent a vector and a scalar condition,

respectively, hence four necessary scalar conditions which must be verified in the

motion of a discrete mechanical system

S with respect to a frame of Koenig; these

conditions are not independent of the seven conditions (the three general theorems),

written with respect to an inertial frame. Obviously, in this case too, all considerations

made for the motion with respect to an inertial frame hold. We can thus obtain a vector

first integral (a conservation theorem of moment of momentum) and a scalar first

integral (a conservation theorem of mechanical energy) in the motion with respect to

the centre of mass, hence four scalar first integrals.

We notice that we can state a theorem of areal velocities and a theorem of areas with

respect to a Koenig frame; as well, one can write a formula of the form (11.1.32''). One

can thus explain the jump of a swimmer from the jumping board (to attain the water in

vertical position, he is varying – by adequate motions – his moment of inertia, hence his

angular velocity with respect to a horizontal axis – the axis of a Koenig frame – which

passes through his centre of mass), the jump of the skier from the spring-board (to reach

the ground in the desired position), the jump of a gymnast on the ground, the fact that a

cat attains the ground on its feet, anyhow it falls, the motions which instinctively we

make by the hands to straighten ourselves in case of a wrong step etc.; in all these cases,

the weight of the considered body is a force passing through the mass centre. We

mention also the manual manoeuvres made by the cosmonauts to direct conveniently

the space vehicles; in this case, the Newtonian force of attraction passes also through

the mass centre of the cabin. As a matter of fact, a general problem of the type

schematized in Fig.11.2 can be considered with respect to a Koenig frame too.

If a mechanical system

S is subjected to the action of a uniform gravitational field

(e.g., a heavy bar, homogeneous or not, launched in the vicinity of the Earth, neglecting

the resistance of the air), then its centre of mass describes a parabola; it remains to

study the relative motion of the system

S (with respect to its mass centre). We can

write a conservation theorem of the moment of momentum (

()C

=KC); assuming that

the system

S is non-deformable, a relation of the form (11.1.32'') with respect to a

fixed axis through the centre of mass, along the direction of the constant

C, takes place,

this system having a motion of rotation about the respective axis (in particular, the bar,

considered to be rigid, is rotating in the plane of maximum of areas, which is normal to

C and which passes through the centre of mass). Indeed, if the direction of the bar is of

unit vector

u, then the velocity of each point of it is along that unit vector, so that

I ×=



uu C, where I is the moment of inertia with respect to the fixed axis, resulting

0⋅=Cu . If, corresponding to the initial conditions, we have =C0, then the

mechanical system

S has a motion of translation with respect to the inertial frame,

being at rest with respect to a Koenig frame. We notice that the external work of the

gravity forces with respect to a Koenig frame vanishes

() () ()

()

333

111

dddd0

nnn

iii

Wmgxgmxgmx

===

=− =− =− =

∑∑∑

assuming that the

-axis is along the ascendent vertical; in this case, the relation

(11.2.8) reads (the discrete mechanical system

S being free, we have

() ()

int

dd0

WW==)

()

int

TW= .

(11.2.8')

If the mechanical system is non-deformable, it results

()

const

T = , hence a

conservation theorem of the kinetic energy with respect to a Koenig frame.

Assuming that the solar system is isolated, it results that its moment of momentum

with respect to the mass centre, situated in the neighbourhood of the mass centre of the

Sun, is constant in time (

()C

=KC

); the plane of maximum of areas, normal to the

constant

C, is an invariable plane for the motions in the interior of this system. Laplace

determined this plane, calculating the components of the moment of momentum

()C

He modelled the planets as particles reduced to their centres of mass; Poinsot completed

this computation, introducing also the influence – in fact, negligible – of the terms

provided by the proper rotation of each planet. These conclusions remain valid even if

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

the influences external to the solar system are not neglected. Indeed, the distances from

other stars to various particles which form the solar system are very great so that the

external forces of Newtonian attraction which act upon these particles and are in direct

proportion to their masses form, with a good approximation, a system of parallel forces,

their resultant moment with respect to the centre of mass vanishing.

11.2.1.3 Problem of n Particles

Returning to the problem of

n particles (see Sect. 1.2.8 too), we will consider the

motion of a discrete mechanical system with respect to the mass centre

C. For 2n = ,

the velocity of the centre of mass with respect to an inertial frame of reference is given

Mm Mm Mm

′′

′′′

′

== =

++ +

HVv

where

′

is the velocity of the Sun S, of mass M, while

′

is the velocity of a planet

P, of mass m, with respect to the same frame; taking into account the conservation

theorem of momentum, we have put in evidence the velocities at the initial moment. In

this case, the velocities of the two particles with respect to a Koenig frame are given by

Fig. 11.7 Problem of two particles

()

′′

−

′′

=− =

VV v

()

′′

−

′′

=− =

vv v

;

(11.2.9)

these velocities have opposite directions at any moment (inclusive at the initial

moment). We notice that the mass centre

C is on the segment of a line SP of length

SP r= , at the distances

r and

r from the centres of the particles S and P,

respectively, so that (Fig. 11.7)

Mr mr= ,

SP S P

Mm Mm

rr r r r

+== =

(11.2.9')

The equation of relative motion of the particle P reads

222

vers

()

PP P

mM mM

mf f

rMmr

=− =−



rr r;

hence, the particle

P moves with respect to the Koenig frame as if it would be

gravitationally attracted by the mass centre

C, at which would be an attractive mass

equal to

32 2

/( ) /(1 / )MMm M mM+= + , describing a conic

()C

C after the law

of areas, the centre

C being at one of the foci. The genus of the conic is specified by the

relations

()2

() ()

Mm Mm

−

P ,

where we have put in evidence the position of the particle

P at the initial moment;

taking into account (11.2.9') and the relation

−=−vv Vv, we find again the

conditions which specified the genus of the conics

C and

C in Sect. 1.2.8.

Analogously, one can also show that the particle

S describes a conic

()C

too, after the

law of areas, with respect to the mass centre, that one being at one of the foci, its genus

being given by the same relations. These conics are situated in the plane determined by

the straight line

PS and by the vector −Vv, being thus coplanar with the conics

C and

C . Taking into account the first relation (11.2.9'), we notice that the two

conics

()C

C and

()C

C are obtained one of the other by a transformation of similitude

(the ratio

/const

rr= ), the centre of similitude being C. We notice that the areal

velocity is constant (

=× =rv cΩ , /2

=× =rV CΩ ) in the motion of

each particle; the plane in which are both trajectories is normal to a fixed direction,

specified by

&cC, and is – in fact – the plane of the maximum of areas. Finally, the

two particles

S and P move so that their mass centre C describes uniformly a fixed

straight line, while the line

SP is rotating about C in a plane of fixed orientation; the

particles

S and P describe conics in this plane, obtained one of the other by similitude

and having one of the foci at

The period of revolution of a particle

P in motion with respect to a Koenig frame is

given by

(

)

(

)

2211

aM m a m m

Ta a k

fM M M

ππ

==+=+

, constk = .

(11.2.9'')

Let us consider, at the atomic level, the motion of an electron about the nucleus; in case

of an atom of hydrogen we have

/1/1850mM= , while in case of an atom of ionized

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

helium

/1/7400mM= . Observing that the wave length is in direct proportion to the

period of revolution

T, we can write for the corresponding wave lengths

(

)

(

)

1111

7400 1850

2468 2500

=+ + =− ≅− ;

experimentally, one obtains

6560.2 Åλ = and

6562.8 Åλ = , so that

He H

/λλ

6560.2/ 6562.8 1 1/2524 1 1/2500=≅−≅−, this result being in good concordance

with the theoretical one.

3n > , then one can follow the considerations in Sect. 1.2.8.

11.2.2 Motion of a Discrete Mechanical System with Respect to

an Arbitrary Non-inertial Frame of Reference

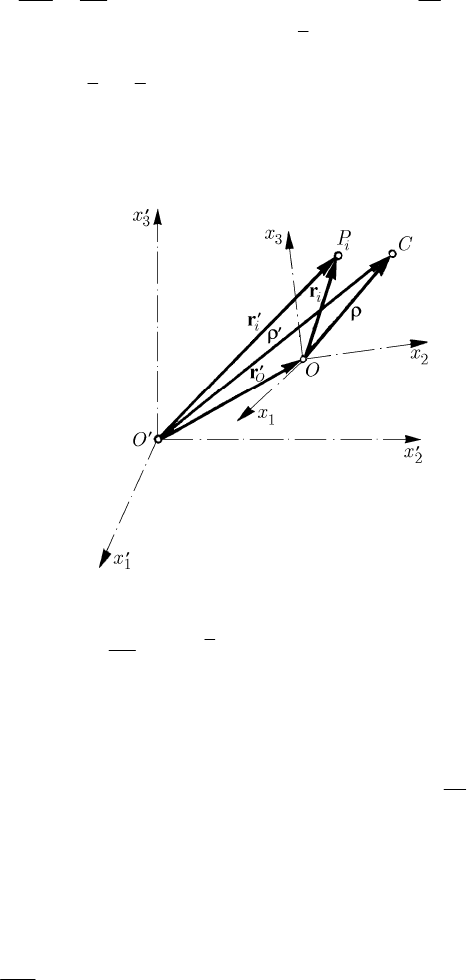
The results obtained in Sects. 11.2.1.1 and 11.2.1.2 will be generalized, assuming that

the movable frame of reference

R has a pole other than the centre of mass of the free

discrete mechanical system

S or/and assuming that the movable frame has a motion of

rotation (

≠ 0ω ) with respect to the fixed frame

′

R . The quantities calculated with

respect to the inertial frame

′

R will be denoted by “prime”, while to the quantities

calculated with respect to the non-inertial frame

R will not be given such a

specification (Fig. 11.8).

11.2.2.1 Momentum and Moment of Momentum with Respect to an Arbitrary

Frame of Reference

We can write

′′

=+rr r

1,2,...,in=

(11.2.10)

for a particle

P , wherefrom, differentiating with respect to the frame of reference

′

R ,

we have

iii

′′

=++×vv v rω

, 1,2,...,in= .

(11.2.10')

Multiplying by the mass

m and summing for all the particles of the system S, we

obtain

()

′′

=+ +×HH v ω

(11.2.11)

ρ being the position vector of the mass centre in the frame R ; we state thus

Theorem 11.2.6 (V. Vâlcovici). The momentum of a discrete mechanical system with

respect to a fixed frame of reference is equal to the sum of the momentum of this system

with respect to an arbitrary frame and the momentum of the mass centre of the system,

considered to be at rest with respect to the latter frame, assuming that its whole mass is

concentrated at this centre, with respect to the fixed frame.

Applying the theorem of momentum with respect to the inertial frame and the

formula (A.2.37), we can write

MM M

tt t

′

∂∂

′′

==+×+ +×+×

∂∂



AHa

ωωρω

()M

′′

+××=+RRωωρ ,

(11.2.11')

where

′

=RR

and

′

=RR

are the resultants of the given and constraint external

forces, respectively; both resultants are invariant by a change of frame. We introduce

the dynamic resultant (11.1.66) with respect to the non-inertial frame

(

/Mt=∂∂H

)

Fig. 11.8 Motion with respect to an arbitrary non-inertial frame of reference

() ()CC

∂

==++ +

∂

ARRFF

(11.2.12)

where the complementary forces (the transportation force and the Coriolis force) are

given by

[]

()

′

=− + × + × ×



Faω

ωω

()

∂

=− ×

∂

ω ,

(11.2.12')

corresponding to the centre of mass (which plays thus an important rôle), where we

consider that the whole mass of the mechanical system

S is concentrated. One can

obtain this result starting from the equations of motion written for a non-inertial frame

(in relative motion)

() ()ii

iiiii

∂

==+++

∂



rFRF F

, 1,2,...,in= ,

(11.2.13)

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

where

[]

()

ii i

′

=− + × + × ×



Far rωωω,

()

m=− ×Fvω

(11.2.13')

and summing for all the particles of the mechanical system

In the particular case in which the frame

R does not rotate (moves with the axes

parallel to themselves) we have

= 0ω and it results

′′

=+HH v,

′

=−Fa,

=F0;

(11.2.11'')

as well, in the case in which the frame

R has its pole at the centre of mass

(

OC≡ , = 0

), we can write

′′ ′

==Hv v,

′

=−Fa,

=F0,

(11.2.11''')

even if

≠ 0ω .

Taking into account the relation (11.2.10'), we have

COC

′′

=++×vvvω

(11.2.14)

wherefrom we obtain

()2

COC C

′′

= + +×+× × + ×



aaa vω

ωω

ω ;

(11.2.14')

observing that

tM∂∂=Ha, the equation (11.2.12), (11.2.12') takes the remarkable

form

′

=+aRR,

(11.2.15)

corresponding to the motion of the centre of mass.

A vector product at the left of the relation (11.2.10') by

′

leads to

()( )

ii i i i i

OO OOO

′′ ′ ′ ′ ′ ′

×= +× ++× =× +×rv r r v v r r v r vω

() ()

iiiiii

′′

+× × − ×+× +× ×rrvrrvrrωω

where we took into account (11.2.10); multiplying by

m and summing for all the

particles of the discrete mechanical system

S, it results

() ()

OO C O

′

′′′ ′

=+× +×

KKr v vρ

(11.2.16)

where we considered (11.2.14) and have introduced a quantity of the nature of a

moment of momentum

()

ii i i ii

=×+×=×

∑∑

Krvrrω

(11.2.16')

We notice that

does not represent the moment of momentum of the discrete

mechanical system

S with respect to the pole O of the non-inertial frame R, taken

with respect to the inertial frame

′

R . But

K represents the moment of momentum of

the discrete mechanical system

S with respect to the pole O, in a non-inertial frame

R , with the pole at the same point O and the axes

Ox parallel to the axes

′′

1, 2, 3i = , of the inertial frame

′

R (because the frame R does not rotate with

respect to the frame

′

R , the derivative with respect to time remains invariant and

d/d

t=vr); this quantity takes a remarkable form by introducing the tensor of

inertia. Thus, observing that

()

() () () ()

() ()

ii ii

iii ii j

ll k

xx xxδω×× = −⋅ = −rrr rr iωωω ,

multiplying by

m , summing for all the particles of the discrete mechanical system S

and introducing the tensor of inertia defined by the relation (3.1.81), we find a relation

of the form (3.1.83) for a quantity

K of the nature of a moment of momentum, which

will be called pseudomoment of momentum of the discrete mechanical system

S with

respect to the pole

O of the non-inertial frame R, i.e.

()

ii i

== ××

∑

KI r rωω,

(11.2.17)

where we have introduced the contracted product of the tensor of inertia at the pole

by the vector angular velocity; it results

=+KKK,

(11.2.17')

where

ii i

=×

∑

Krv

(11.2.17'')

is the moment of momentum of the discrete mechanical system

S with respect to the

pole

O of the non-inertial frame R. We state

Theorem 11.2.7 (V. Vâlcovici, C. Iacob). The moment of momentum of a discrete

mechanical system with respect to a pole

′

of a given inertial frame of reference

′

R , in this frame, is equal to the sum of the moment of momentum of this system with

respect to an arbitrary pole

O of a non-inertial frame R (which does not rotate with

respect to the frame

′

R ), in the latter frame (the sum of the moment of momentum of

the system with respect to the pole

O in a non-inertial frame R, with the pole at the

very same point, and the contracted product of the tensor of inertia with respect to the

11 Dynamics of Discrete Mechanical Systems