Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

respect to the time

t is reduced to the corresponding partial derivative ( / tΦΦ=∂ ∂



/ t=∂ ∂



ΨΨ

, respectively); this derivative is called material derivative. We notice that

one can use the relation (12.1.3) also in the form

(;)t=−rrur

(12.1.3'')

×DT

Fig. 12.1 Material and spatial co-ordinates

In a spatial description (convenient in case of fluids) we define the characteristic

quantities (velocity, density, pressure etc.) as functions of

r and t; e.g., to have (;)tvr

means to know the velocities of all particles (at any moment) which pass through all the

points

P (of the domain D ). From the equations

(;)

r ,

1,2, 3i =

(12.1.4)

we obtain the trajectories of motion; indeed, if the solution exists and is unique, then we

can write the independent first integrals

123

(,, ;)

xxxt C= , const

C = ,

1,2, 3i =

which, on the basis of the theorem of implicit functions, lead to the relations (12.1.2)

(we assume that for

tt= we have

xx= , hence

()

000

1230

,,;

C fxxxt= ). But, in

general, it is sufficient to determine fields (e.g., scalar fields) of the form

(;)

ft= r ;

the derivative of such a quantity with respect to time (the material derivative) is given

by the formula

vf f f

ttxt

∂∂

= + =+ =+⋅

∂∂



v ∇ ,

(12.1.5)

×DT. Analogously, one obtains the material derivative of a vector field too; the

acceleration is given by

()

==+⋅



avvv

∇

(12.1.6)

×DT

. If we take into account the relation (12.1.2), then we notice that a quantity

(;)

tr , defined in spatial co-ordinates, may be studied in a material description in the

form

(;) (( ;);)

tf tt=rrr.

12 Dynamics of Continuous Mechanical Systems

We call material variety (point, curve, surface, three-dimensional domain) a variety

formed of particles; often, the use of such a variety can very much simplify the study of

the motion of the considered mechanical system

S. In conformity to the conservation

theorem of material varieties, their images are varieties of the same order. Taking into

account the conditions (3.2.18) imposed to a particle subjected to finite constraints, one

can show that (Euler-Lagrange criterion) a surface of equation

(;) 0tΦ =r is material

(is the image of a material surface) if (necessary and sufficient condition)

grad 0

ΦΦ

=+⋅ =



v .

(12.1.7)

In case of a vector field

(;)trΨ , its lines are material curves if and only if the formula

(Helmholtz-Zorawski criterion)

[

]

curl( ) div×+ ×+ =



vv 0

ΨΨ Ψ Ψ

(12.1.8)

which can be put in connection with the formula (A.2.81'), holds. In particular, for

= vΨ it results

×=vv 0, (12.1.8')

that is the necessary and sufficient condition for the field lines (current lines) of the

velocity to be trajectories.

The mass

()m S of the mechanical system S (including a continuous mechanical

system) has been introduced in Chap. 1, Sect. 1.1.6, its mathematical model having

certain properties: i)

()0m >S ; ii) the property of additivity; iii)

0m = .

Differentiating in the sense of the theory of distributions, we find the density

(;)tμμ= r , which is given by the relation (1.1.71).

Besides the formulae given in Chap. 1, Sect. 1.1.9 and in Ann., Sect. 2.3.5, it is

useful to establish other two formulae of differentiation for the integrals which depend

on a parameter. Let be such an integral of the form

123 123

()

(,, ;)(,, ;)d

I Fxxxt xxxtμτ≡

∫∫∫

(12.1.9)

where dτ is the element of volume. Observing that

div( ) div( )FFμμ=vv

gradFμ+⋅v , we may write

()

() ()

div( ) d grad d

Dt Dt

tt t

μτ μ τ

∂

⎡⎤

=+++⋅

⎢⎥

∂∂

⎣⎦

∫∫∫ ∫∫∫

vv;

according to the relation (1.1.79'), the first integral vanishes, while the relation (12.1.5)

allows to write

()

μτ=

∫∫∫

(12.1.9')

MECHANICAL SYSTEMS, CLASSICAL MODELS

Analogously, for the vector integral

()

(;)(;)d

ttμτ≡

∫∫∫

IVrr

(12.1.10)

we obtain

()

μτ=

∫∫∫

(12.1.10')

We notice that the physical properties of material bodies, which are modelled as

mechanical systems, do not depend neither on the frame of reference, nor if that one is

at rest or in motion; hence, these properties are characterized by objective quantities

(independent on the frame), which satisfy the principle of objectivity (the principle of

material indifference, the principle of frame independence). The most general relation

between co-ordinates and time with respect to a frame

R and a chronology C or a

frame

′

and a chronology

′

, respectively, is of the form

()

( ) () ()

iijjji

xt Q t x x ct

′′

=−+, 1, 2, 3i = ,

ttt

′

=+ ,

,const

xt= ,

(12.1.11)

where

Q is a proper orthogonal matrix (

==QQ Q Q I , det 1=Q ), the frames

being right-handed orthonormed, while

()tc is a vector. A scalar quantity s is objective

(;) (;)stst

′′

=rr,

(12.1.12)

a vector quantity

V is objective if

(;) ()(;)ttt

′′′

=Vr Q Vr ,

iijj

VQV

′

, 1, 2, 3i = ,

(12.1.12')

while a tensor quantity

T of second order is objective if

(;) ()(;) ()tttt

′′′

=Tr Q Tr Q ,

ik jl kl

TQQT

′

, ,1,2,3ij= .

(12.1.12'')

Because the considered frames are movable (

()t=QQ and ()t=cc), these relations

are different from those which define a scalar, a vector or a tensor of second order. One

can easily see that the position vector, the velocity and the acceleration are not objective

vectors. The unit mass is an objective scalar.

12.1.1.2 General Principles

The principles of mechanics, so as they have been enounced in Chap. 1, Sect. 1.2.1 for

a particle and as they have been used in Chap. 11 for a discrete mechanical system (a

finite number of particles), cannot satisfactorily describe the evolution of a continuous

12 Dynamics of Continuous Mechanical Systems

mechanical system

S. To pass from discrete to continuum, from a finite to an infinite

number of particles, it is necessary much rigour; as a matter of fact, this represents the

passing from a finite number to an infinite number of degrees of freedom (excepting the

case of the rigid solid). Indeed, the notion of particle (of finite positive mass) loses its

sense, because it would lead to an infinite mass for the mechanical system

S. The

notions of velocity and acceleration are linked to a point (hence to a particle), so that

Newton’s law (1.1.89) can no more be applied in this form; as a matter of fact, all

principles of mechanics must be formulated of new and consequently adapted. The

principles which allow the mathematical modelling of a continuous mechanical system

must be formulated so as to can reduce them to Galileo-Newton principles in case of a

discrete mechanical system.

To express these principles, we denote by

S a subsystem of the system S, D ⊂ D

being the domain occupied by that one, while

ωΩ⊂

is its geometric support. The

principles of motion of the continuous deformable media are expressed by balance

relations of the form

dddd

DDD

mVSV

μμ

∂

==+

∫∫∫ ∫∫∫ ∫∫ ∫∫∫

QQRnS, D∀⊂D ,

(12.1.13)

where

Q and S are tensors of the same order defined on D × T , while R is a tensor of

an order greater with a unity, defined on

D × T

DD D=∪∂

; hence, at any

moment

t, the increasing (or decreasing) of a quantity of density μ for any subsystem S

is due to a flux of entering (or exit) through

D∂ and of positive (or negative) internal

sources, μ

S being their intensity on the unit volume. Applying the formula (12.1.10') to

the integral at the left, as well as a formula of flux-divergence type (of the type of the

formula (A.2.67)), we get

()

ddivd

VVμμ=+

∫∫∫ ∫∫∫



QRS

D∀⊂D

;

assuming that R are fields of class

()CD and μ



and μS are fields of class

()CD

and observing that

D is an arbitrary subdomain, we obtain the local form of the balance

equations (for continuous motions)

div μμ+=



RSQ

(12.1.13')

We can enounce thus four important principles, i.e.:

Conservation principle of mass. The mass ()mS of any subsystem S ⊂ S is

conserved during the motion.

This principle, which synthesizes all the three axioms at the basis of the definition of

mass, may be expressed in the form

() 0mS =



, S∀⊂S ,

(12.1.14)

MECHANICAL SYSTEMS, CLASSICAL MODELS

and may be obtained from (12.1.13) if one makes

==RS0 and

=QI

. In a material

description, one gets d’Alembert’s condition of mass continuity (1.1.76), while, in a

spatial description, it results Euler’s condition of mass continuity in the form (1.1.79) or

in the form (1.1.79'). The latter relation is equivalent to

div( ) d 0

∂

⎡⎤

⎢⎥

∂

⎣⎦

∫∫∫

v .

Applying the Gauss-Ostrogradskiĭ formula (A.2.67), we obtain

∂

=− ⋅

∂

∫∫∫ ∫

vn , D∀⊂D ;

(12.1.15)

this equation (called transportation equation of mass) shows that the mass variation of

D in a unity of time (the left member) is due to the flux of matter through the frontier

∂

D (we are led to a decrease of mass if 0⋅>vn or to an increase of mass if

0⋅<vn ).

ii)

Principle of internal forces (Cauchy). For any subsystem S ⊂ S which

occupies the domain

D ⊂ D there exists a distribution of internal forces p on the

frontier ∂

D, the action of which upon the subsystem S is equivalent to the action of the

subsystem

SS 3 upon the same subsystem.

Fig. 12.2 Continuous mechanical system. Internal forces (a);

stress vector (b); body force (c)

This principle is, in fact, a postulate of existence. It corresponds to the Theorem

11.1.27 of dynamic equilibrium of parts for discrete mechanical systems, being an

extension of it for a continuous case (Fig. 12.2a). In case of a discrete mechanical

system, upon a subsystem of it may act external forces on a part of the frontier (which

can be also zero) and internal forces on the rest of it (which can be the whole frontier

too); analogously, a particle subjected to constraints may be considered as being a

subsystem of the system formed by that particle and the subsystem which generates the

constraints. In case of a continuous mechanical system arises just such a situation,

where the internal forces

p are not known a priori; they must be determined using the

equations of motion (equilibrium). The superficial forces

p represent a density and

12 Dynamics of Continuous Mechanical Systems

form – obviously – an absolutely continuous surface field. Corresponding to Cauchy’s

mathematical modelling, the internal force

p at a point P of position vector r on ∂D is

the same for all surfaces of same external normal

n and of same tangent plane at P; this

dependence is expressed in the form (Fig. 12.2b)

(,;)t=ppnr,

(12.1.16)

the vector

p (denoted sometimes by (;)

t=ppr) being called stress vector. In case of a

fluid, the internal normal (of unit vector −

n) is used, because the stress vector

corresponds to a predominant phenomenon of compression (in case of a deformable

solid, both compression and stretching appear).

Besides the stress vectors

p, which represent contact actions, we will consider

actions at distance too, expressed by a field of body (mass) forces

F, referred to a unit

mass, which we assume to be absolutely continuous functions of volume. Unlike the

stress vectors, which depend on the configuration of the continuous mechanical system,

the body forces do not depend on this configuration (

(;)t=FFr, Fig. 12.2c). As the

contact actions, the actions at distance are represented by objective quantities; such

quantities are the body force

F (

′

FQF) and the stress vector p (

′

pQp).

We have seen that the principle ii) corresponds to the theorem of dynamic

equilibrium of parts. In the mathematical modelling of a continuous mechanical system,

we use – further – the results obtained for discrete mechanical systems, adapting them

consequently. Thus, the theorem of rigidity, which – applied to all subsystems of a

discrete mechanical system – gives sufficient equations to describe the motion of that

system, may be extended to a continuum, enouncing

iii)

Principle of variation of kinetic torsor. The derivative with respect to time of

the kinetic torsor of any subsystem

S ⊂ S , in any of its configurations, with respect to

a fixed pole, is equal to the torsor of the forces which act upon that subsystem, with

respect to the same pole.

Obviously, the forces which act upon the considered subsystem

S are body forces F

(given forces) and internal forces p (forces linking with the subsystem SS 3 ),

postulated by Cauchy. As well, we assume the existence of an inertial frame of

reference and of a chronology with respect to which we may enounce this principle. In

fact, this principle contains two parts:

iii

) Principle of variation of momentum. The derivative with respect to time of the

momentum of any subsystem

S ⊂ S , in any of its configurations, is equal to the

resultant of the forces which act upon that subsystem.

Starting from the relation of definition (11.1.1) of the momentum of an arbitrary

mechanical system

S, we can write

() (;)(;)d

SttVμ=

∫∫∫

Hrvr

(12.1.17)

for a subsystem

S ⊂ S of a continuous mechanical system, where D is the domain

occupied by that subsystem in the actual state, at the moment

t. Introducing the actions

of contact and at distance mentioned above, we may express this principle in the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

dd d

DDD

VS V

μμ

∂

∫∫∫ ∫∫ ∫∫∫

vp F, D∀⊂D .

(12.1.17')

iii

) Principle of variation of moment of momentum. The derivative with respect

to time of the moment of momentum of any subsystem

S ⊂ S , in any of its

configurations, with respect to a fixed pole, is equal to the moment of the forces which

act upon that subsystem, with respect to the same pole.

The relation of definition (11.1.2) of the moment of momentum of an arbitrary

mechanical system

S with respect to a given pole O leads to

[]

() (;)(;)d

SttVμ=×

∫∫∫

Krrvr

(12.1.18)

for the subsystem

S ⊂ S of a continuous mechanical system. Putting in evidence the

moment of the forces of contact or at distance considered above, we have

()d d ()d

DDD

VS V

μμ

∂

×=×+×

∫∫∫ ∫∫ ∫∫∫

rv rp rF, D∀⊂D .

(12.1.18')

In the case in which

S ≡ S , it results D ≡ D , while the stress vectors

p become

given external superficial forces. The two equations (12.1.17'), (12.1.18') have, in this

case, the advantage to contain only given external forces, hence known ones, but

represent only necessary conditions to describe the motion of the continuous

mechanical system

The formula (12.1.10') allows to express the equations (12.1.17'), (12.1.18') also in

the form

dd d

DDD

VS Vμμ

∂

∫∫∫ ∫∫ ∫∫∫

ap F, D∀⊂D ,

(12.1.19)

()d d ()d

DDD

VS Vμμ

∂

×=×+×

∫∫∫ ∫∫ ∫∫∫

ra rp rF, D∀⊂D ,

(12.1.19')

being thus led to another principle, equivalent to the principle iii); we may enounce

iii')

Principle of variation of the dynamic torsor. The dynamic torsor of any

subsystem

S ⊂ S , in any of its configurations, with respect to a fixed pole, is equal to

the torsor of the forces which act upon that subsystem, with respect to the same pole.

This principle contains the principle of variation of the dynamic resultant (12.1.19)

and the principle of variation of the dynamic moment (12.1.19').

The conditions of static equilibrium are obtained writing that the position vector of

each particle remains constant in time (

=v0); 0t∀≥ , these conditions have the form

SVμ

∂

∫∫ ∫∫∫

pF0,

D∀⊂D

(12.1.20)

d()d

SVμ

∂

×+ × =

∫∫ ∫∫∫

rp r F 0,

D∀⊂D

(12.1.20')

Applying the principle of variation of momentum to a subdomain of the form of a

cylinder the height of which tends to zero, we may state

12 Dynamics of Continuous Mechanical Systems

Theorem 12.1.1 (Cauchy). At the same point of a continuous mechanical system and at

the same moment, the stress vector verifies the relation

(,;) ( ,;)tt=− −pnr p nr .

(12.1.21)

Considering a domain in the form of a three-orthogonal tetrahedron, for which the

height relative to the inclined face tends to zero, and applying the principle of variation

of momentum, we find the relation

(,;) ( ,;)

ttn=pnr pi r

(12.1.22)

where

n are the components of the unit vector n of the external normal to the element

of surface which passes through the point

P of position vector r. Projecting this relation

on the co-ordinate axis of unit vector

i , we can state

Theorem 12.1.2 (Cauchy’s basic theorem). The state of stress (the stress vector p)

around a point of a continuous mechanical system may be linearly expressed by means

of a tensor of second order (the stress tensor σ) in the form

(,;) (;)tt=pnr r nσ

pnσ= , (,;)

ij j i

ptσ = ir ,

,1,2,3

ij=

(12.1.22')

Applying also the principle of variation of moment of momentum to the same domain,

one can see that the stress tensor is symmetric (the relation

=σσ,

ij ji

σσ= ,

,1,2,3ij= , takes place). We notice that the tensor σ defined on D is an objective one.

Taking into account the Theorem 12.1.2, we can write the principles iii

) and iii

) by

means of the balance equations

ddd

DD D

VSV

μμ

∂

∫∫∫ ∫∫ ∫∫∫

vnFσ , D∀⊂D ,

(12.1.23)

()d ( )d ()d

DD D

VSV

μμ

∂

×=× +×

∫∫∫ ∫∫ ∫∫∫

rv r n rFσ

D∀⊂D

(12.1.23')

which are of the form (12.1.13); the local form of those balance equations is

div μμ+=Faσ ,

ij i i

Faσμμ+=, 1, 2,3i = .

(12.1.23'')

Assuming that

(,;)tpnr is the given superficial force which acts upon the

continuous mechanical system

S (the jump of the stress vector by passing through the

frontier ∂

D is equal to zero), the basic theorem of Cauchy, expressed in the form

(12.1.22'), allows to put the boundary conditions in stresses at any moment

tt≥ . For

a complete formulation of the boundary value problem of a continuous mechanical

system we enounce also

iv)

Principle of initial conditions. The evolution of a continuous mechanical system

S may be determined

tt∀> if the state (positions and velocities) of that system at

the initial moment

t is known.

MECHANICAL SYSTEMS, CLASSICAL MODELS

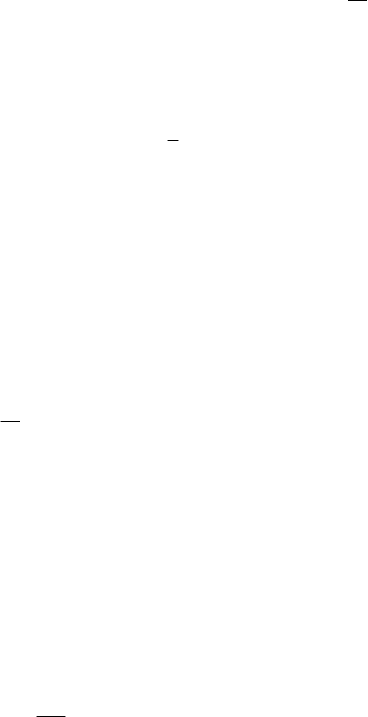
This principle puts in evidence the deterministic aspect of classical models of the

continuous mechanical systems (in general, of any mechanical system).

Corresponding to the ideas expressed in Chap. 11, Sect. 1.2.7, we can enounce the

first principle of thermodynamics (see relation (11.1.47''') in the form

int

dd( )d d ddETVE WQW=++ =++, D∀⊂D ,

(12.1.24)

where

V is the potential energy, T is the kinetic energy given by (11.1.6) and expressed

in the form

() (;) (;)d

TS tv t Vμ=

∫∫∫

rr ,

(12.1.25)

D being the domain occupied by the subsystem S ⊂ S in the actual state at the

moment

int

E is the internal energy (an objective scalar state quantity) of the

subsystem

S, due to the internal non-conservative forces and postulated as an absolutely

continuous function of mass, having the form (

e is the unit internal energy, an objective

quantity too)

int

() d (;)(;)d

ES em tetV

μ==

∫∫∫ ∫∫∫

rr ,

(12.1.26)

while

dW is an elementary work of non-mechanical and non-calorical nature (e.g., of

electromagnetic nature); the sum

int

ETVE=++ is called total energy. In case of a

continuous mechanical system

S, adiabatically non-isolated, the quantity of energy

may be increased by a flux of heat d

Q, even without the intervention of an external

mechanical work (if the mechanical system

S is adiabatically isolated, then we have

Q = ); we can express d/dQt as a sum of a function q, absolutely continuous of

area (an action of contact, due to the phenomenon of conduction), and a function

absolutely continuous of volume (an action at distance, due to the phenomenon of

radiation or due to thermal sources)

(,;)d (;)(;)d

qtS trtV

∂

∫∫ ∫∫∫

nr r r ,

(12.1.27)

where

r is a unit quantity (with respect to the unit mass), while q is a quantity given by

(,;) (;)qt t=− ⋅nr n qr ,

(12.1.27')

q being the heat current density vector (the sign − puts in evidence the internal normal,

corresponding to the heat received). The relation (12.1.27') represents the Fourier-

Stokes principle of heat flux, corresponding to the basic theorem of Cauchy. The

elementary work of the forces which act upon the subsystem

S ⊂ S , in the actual

configuration at the moment

t, is expressed in the form

12 Dynamics of Continuous Mechanical Systems

d(,;)dd(;)(;)dd

WtSttVμ

∂

=⋅+ ⋅

∫∫ ∫∫∫

pnr r r Fr r ,

(12.1.28)

the power of those forces being given by

(,;) (;)d (;)(;) (;)d

PttStttV

∂

== ⋅ + ⋅

∫∫ ∫∫∫

pnr vr r Fr vr .

(12.1.28')

Analogously, the power of actions of non-mechanical and non-calorical nature will be

(12.1.29)

The principle of energy variation can be written in the form

int

d( )

dd d

tt t

+=++

, D∀⊂D ,

(12.1.24')

corresponding to the first principle of thermodynamics (12.1.24). Taking into account

(12.1.25) and (12.1.28'), as well as the differentiation formula (12.1.10'), we can write

this principle in the form

int

∂

⋅++ = ⋅

∫∫∫ ∫∫

vv pv

μ+⋅++

∫∫∫

Fv , D∀⊂D .

(12.1.24'')

Putting the condition that the principle of energy variation be invariant to rigid

displacements, A.E. Green and R.S. Rivlin have shown that, starting from this principle,

one can obtain the principle of torsor variation. For instance, if the relation (12.1.24'')

takes place for any field of velocities, hence for the field of velocities

+vc

const=

JJJJG

c , too, then we may write

int

()d ()d

∂

+⋅ + + = ⋅+

∫∫∫ ∫∫

vcv pvc

()d

μ+⋅+++

∫∫∫

Fvc , D∀⊂D ;

taking into account (12.1.24''), there results

()

dd d0

DDD

VS Vμμ

∂

⋅−− =

∫∫∫ ∫∫ ∫∫∫



cv p F, D∀⊂D .

But the velocity

c is arbitrary, hence the parenthesis vanishes; thus, we find again the

principle of variation of the dynamic resultant, equivalent to the principle of variation

of momentum.

Assuming that the mechanical system

S is adiabatically isolated ( d/d 0Qt= ) and

that the power

P vanishes ( 0P = ), we write the power P in the form (we take into

MECHANICAL SYSTEMS, CLASSICAL MODELS