Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems
Подождите немного. Документ загружается.


account the basic theorem of Cauchy and use the Gauss-Ostrogradskiĭ formula
(A.2.67), observing that
T
() ( ) ( ) ()
ji j i ji i j
nv vnσσ⋅===⋅nv vnσσ,
()
[]
T
dddiv()d
DDD
PSV Vμμ
∂
=⋅+⋅= +⋅
∫∫ ∫∫∫ ∫∫∫
nv Fv v Fvσσ
[]
()
[]
,,,
() d d
ji i j i i ji j i i ji i j
DD
vFvV FvvVσμ σμσ=+=++
∫∫∫ ∫∫∫
()d
ii ijij
D
va a Vμσ=+
∫∫∫
,
where we have used the decomposition
[]
,
,
(,)
ij
ij
ij
vv v=+, we have noticed that
[]
,
0
ij
ij
vσ = and we have introduced the deformation velocity tensor
()
,,
(,)
1
2
ij i j j i
ij
av v v== +;
(12.1.30)
finally, we can write (a generalization of Clapeyron’s principle, corresponding to the
static case)
d
d
T
PP
t
′
=+
, D∀⊂D ,
(12.1.31)
where
d
ij ij
D
PaVσ
′
=
∫∫∫
(12.1.32)
represents the variation of deformation energy.
We mention that, in the static case,
ij
a is replaced by the strain tensor
()
,,
(,)
1
2
ij i j j i
ij
uuuε == +,
(12.1.30')
the velocity
v being replaced by the displacement u.
In case of conservative internal forces, we have
d/dPVt
′
= , the contribution of
eventual non-conservative internal forces (or of a non-conservative part of them) being
contained in
int
d/dEt.
Obviously, the first principle of thermodynamics (12.1.24), as well as the principle
of variation of energy (12.1.24') (or (12.1.24'')) or the generalization (12.1.31) of
Clapeyron’s principle may be written for a continuous mechanical system
S
(corresponding to the domain
D) too; but these relations represent only necessary
conditions to describe the motion.
93
12 Dynamics of Continuous Mechanical Systems

12.1.2 General Theorems. Conservation Theorems
In what follows, we present the universal theorems for a continuous mechanical system,
both for an inertial and a non-inertial frame of reference; starting from these theorems,
we put in evidence some conservation theorems.
12.1.2.1 General and Conservation Theorems with Respect to an Inertial Frame
of Reference
Starting from the principle of variation of the torsor, enounced in the preceding
subsection, we can write (corresponding to the relations (11.1.53) and (11.1.53'') too)
d
dt
=+
H
RR
, (;)(;)dttVμ=
∫∫∫
D
Hrvr,
1
n
i
i =
=
∑
RF
,
1
n
i
i =
=
∑
RR
,
(12.1.33)
d
d
O
O
O
t
=+
K
MM,
[]
(;)(;)d
O
ttVμ=×
∫∫∫
D
Krrvr,
1
n
ii
O
i
=
=×
∑
MrF
,
1
n
O
ii
i
=
=×
∑
MrR
,
(12.1.33')
for the continuous mechanical system
S, where
i
F and
i
R , 1,2,...,in= , are given
and constraint external forces which act upon this system; we can add to these forces
also absolute continuous body forces, as in the formulae (12.1.17') and (12.1.18'). We
thus state:
Theorem 12.1.3 (theorem of momentum). The derivative with respect to time of the
momentum of a continuous mechanical system subjected to constraints is equal to the
resultant of the given and constraint external forces which act upon that system.
Theorem 12.1.4 (theorem of moment of momentum). The derivative with respect to time
of the moment of momentum of a continuous mechanical system subjected to
constraints, with respect to a fixed pole, is equal to the resultant moment of the given
and constraint external forces which act upon that system, with respect to the same
pole.
These theorems take place for both holonomic and non-holonomic constraints; as
well, we can assume the existence of unilateral constraints. The above mentioned
theorems can be included in
Theorem 12.1.5 (theorem of kinetic torsor). The derivative with respect to time of the
kinetic torsor of a continuous mechanical system subjected to constraints, with respect
to a fixed pole, is equal to the torsor of the given and constraint external forces which
act upon that system, with respect to the same pole.
Introducing the impulse of the resultant of the given and constraint external forces,
as well as the impulse of the resultant moment of the same forces in a given interval of
time, one can write relations of the form (11.1.54 to 11.1.54'') concerning the finite
variation of the quantities considered above. Analogously, we can state
Theorem 12.1.6 (theorem of dynamic torsor; Newton-Euler). The dynamic torsor of a
continuous mechanical system subjected to constraints, with respect to a fixed pole, is
94
MECHANICAL SYSTEMS, CLASSICAL MODELS

equal to the torsor of the given and constraint external forces which act upon that
system, with respect to the same pole.
This theorem includes the theorems of dynamic resultant and of dynamic moment.
Let be a continuous mechanical system
S, the support of which is the domain D,
separated into two subsystems
1
S and
2
S (
12
∪=SSS,
12
∩=∅SS ), of
supports
1
D and
2
D , and let be
{
}
11
,RM and
{
}
22
,RM the torsors of the external
forces acting upon the subsystems
1
S and
2
S , respectively, with respect to the same
pole
O; corresponding to the principle ii), we denote by
{
}
12 12
,RM and
{
}
21 21
,RM
the torsors of the internal forces with which the subsystem
2
S acts upon the subsystem
1
S and with which the subsystem
1
S acts upon the subsystem
2
S , respectively, with
respect to the mentioned pole
O. The theorem of torsor (in one of the two forms) allows
to write
1
112
d
d
d
V
t
μ =+
∫∫∫
D
vRR,
2
221
d
d
d
V
t
μ =+
∫∫∫
D
vRR,
12
d
d
d
V
t
μ =+
∫∫∫
D
vRR,
1
112
d
()d
d
V
t
μ×=+
∫∫∫
D
rv MM,
2
221
d
()d
d
V
t
μ×=+
∫∫∫
D
rv MM,
12
d
()d
d
V
t
μ×=+
∫∫∫
D
rv MM;
taking into account the property of additivity of the integral, we get
12 21
+=RR 0,
12 21
+=MM 0, (12.1.34)
so that we can state
Theorem 12.1.7 (theorem of action and reaction). Be given a mechanical system S, the
torsor of the actions exerted by a subsystem
1
⊂SS upon another subsystem
2
⊂SS (
12
∪=SSS,
12
∩=∅SS ) equilibrates the torsor of the actions
(reactions) exerted by the subsystem
2
S upon the subsystem
1
S .
If, in particular, both subsystems are reduced to two particles
1
P and
2
P , then the
relations (12.1.34) become
12 21
+=RR 0,
12 1 2
PPλ=
J
JJJG
R , λ scalar,
(12.1.34')
finding again the principle of action and reaction in Newton’s formulation.
Starting from the relation (3.1.3), we can write the position vector of the centre of
mass of the subsystem
S ⊂ S
in the form
1
() (;)d
()
D
StV
mS
μ=
∫∫∫
rrρ , D∀⊂D ;
(12.1.35)
95
12 Dynamics of Continuous Mechanical Systems

taking into account the differentiation formula (12.1.10') and the formula (12.1.17), we
get
() () ()
C
SmS S=Hv, S∀⊂S .
(12.1.35')
Differentiating once more with respect to time and taking into account the principle iii
1
)
of variation of the impulse, expressed in the form (12.1.17'), we can write
() () d d
n
C
DD
mS S S Vμ
∂
=+
∫∫ ∫∫∫
apF, D∀⊂D ;
(12.1.36)
we enounce thus (a principle equivalent to the principle iii
1
) or a theorem, considered as
a consequence of the latter principle)
iii'
1
) Principle of motion of the centre of mass. The centre of mass of any
subsystem
S ⊂ S
, in any configuration of it, is moving as a free particle, where it is
supposed to be concentrated the whole mass of that subsystem and which is acted upon
by the resultant of the forces which act upon it.
For the continuous mechanical system
S of mass M it results
C
M =+aRR,
(12.1.36')
so that we can state
Theorem 12.1.8 (theorem of motion of the centre of mass). The centre of mass of a
continuous mechanical system subjected to constraints is moving as a free particle at
which would be concentrated the whole mass of that system, being acted upon by the
resultant of the given and constraint external forces.
If the moment of momentum is calculated with respect to a pole
Q rigidly linked to
the inertial frame
R, then both the principle of moment of momentum and the theorem
of moment of momentum remain, further, valid. If the pole
Q is movable, but the
computation is effected with respect to the same inertial frame
R, then
()
OQ
OQ=+×+
J
JJG
KK RR
and
d
d
Q
Q
QQ
t
=+−×
K
MMvH
.
(12.1.37)
In the case in which
dd 0QW==, we can state (we use the same formula
(11.1.55))
Theorem 12.1.9 (theorem of kinetic energy). The differential of the kinetic energy of a
continuous mechanical system subjected to constraints is equal to the elementary work
of the given and constraint external and internal forces which act upon that system.
In case of scleronomic constraints we have
int
dd 0
RR
WW==
; the theorem of
kinetic energy takes a simpler form (
int
dd dTWW=+
), eventually the form
(12.1.31), written for the whole domain
D.
As in the case of a discrete mechanical system (see Sect. 11.1.2.9), we can obtain, in
certain conditions, conservation theorems also for the continuous mechanical system
S.
96
MECHANICAL SYSTEMS, CLASSICAL MODELS
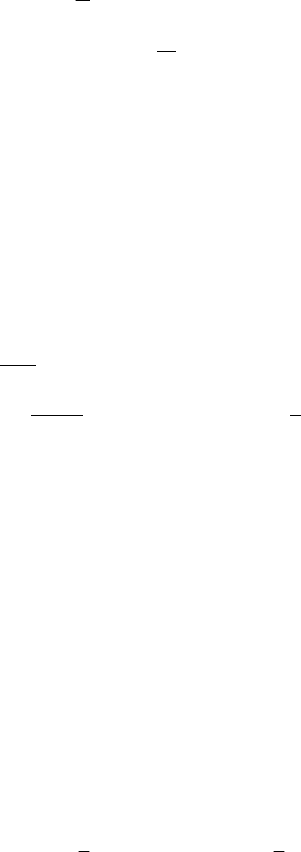
Thus, if
+=RR0
(necessary condition for statical equilibrium), then we can state a
conservation theorem of momentum, the mass centre having a rectilinear and uniform
motion, while if
O
O
+=MM0
(necessary condition for statical equilibrium), then we
can state a conservation theorem of moment of momentum.
In case of scleronomic constraints and of internal conservative forces (the stress
tensor derives from a potential) we obtain a relation of the form (corresponding to the
relation (12.1.31))
int
dddWTW=+ , (12.1.38)
where the external work (given by loading of the mechanical system
S by external
loads), the internal work (corresponding to the unloading of the system
S ) and the
kinetic energy are given by
d
(;) (;)d (;) (;) (;)d
d
n
W
ttS tttV
t
μ
∂
=⋅+ ⋅
∫∫ ∫∫∫
DD
pr vr r Fr vr ,
int
d
d
d
ij ij
W
aV
t
σ=
∫∫∫
D
,
2
1
(;) (;)d
2
TtvtV
μ=
∫∫∫
D
rr ,
(12.1.39)
respectively.
Assuming, in case of a deformable solid, that the natural state of stress (the state of
stress – the existence of which is supposed – for which all the stresses vanish) and the
initial state of deformation (for which all the quantities which characterize the
deformation are – by definition – equal to zero) correspond to the initial moment
0t = ,
then one obtains a generalization of Clapeyron’s theorem of the statical case
int
WTW=+ ; (12.1.38')
in fact, that is a conservation theorem of energy. In the statical case (
0T = ), it results
Clapeyron’s theorem in the form
int
WW= , (12.1.38'')
with
11
() ()d ()() ()d
22
n
WS Vμ
∂
=⋅+ ⋅
∫∫ ∫∫∫
DD
pr ur rFr ur ,
(12.1.39')
where
()ur is the displacement vector.
12.1.2.2 General and Conservation Theorems with Respect to a Non-inertial
Frame of Reference
We refer the continuous mechanical system
S to an inertial (fixed) frame of reference
′
R
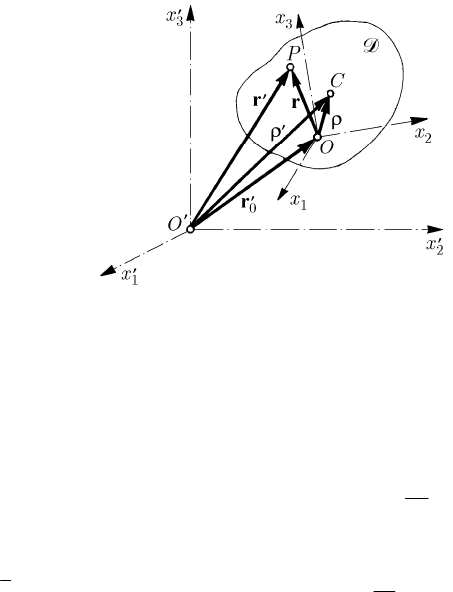
and to a non-inertial (movable) frame R (Fig. 12.3), using the notations in Sect.
11.2.2. We can write
97
12 Dynamics of Continuous Mechanical Systems
O
′′
=+
rr r,
O
′′
=++×
vv v rω
(12.1.40)
for a particle
P. Defining the momentum of this system in the form
dVμ
′′
=
∫∫∫
D
Hv
(12.1.41)
and taking into account
dMVμ=
∫∫∫
D
, dMVμ=
∫∫∫
D
rρ ,
(12.1.40')
we obtain the formula (11.2.11) too, the Theorem 11.2.6 remaining valid also for a
continuous mechanical system. As well, applying the theorem of momentum, we find
again the equation (11.2.15), corresponding to the motion of the mass centre.
Fig. 12.3 Inertial frame of reference
′
R and non-inertial frame of reference R
The moment of momentum is defined in the form
()d
O
Vμ
′
′′′
=×
∫∫∫
D
Krv;
(12.1.42)
taking into account (12.1.40), (12.1.40'), we find again the formula (11.2.16) of the
moment of momentum, where the velocity
C
′
v is given by (11.2.14) and where the
moment of momentum with respect to a non-inertial frame
R , which does not rotate
about the inertial frame
′
R , is expressed in the form
d
()d d
d
O
VV
t
μμ=×+×=×
∫∫∫ ∫∫∫
DD
r
Krvr r
ω .
(12.1.43)
Introducing at the pole
O the tensor of inertia defined by the relation (3.1.81) and using
the contracted product of this tensor by the angular velocity rotation vector, we get
()d
O
Vμ ×× =
∫∫∫
D
rrIωω,
(12.1.44)
98
MECHANICAL SYSTEMS, CLASSICAL MODELS

being thus lead to the relation (11.2.17') too, where the moment of momentum of the
continuous mechanical system
S with respect to the pole O of the non-inertial frame
R is given by
d
O
Vμ=×
∫∫∫
D
Krv.
(12.1.42')
The Theorem 11.2.7 may be thus stated for a continuous mechanical system
S too,
while the theorem of moment of momentum maintains its form (11.2.18), (11.2.18'),
observing that the relation
()d ()d
O
VV
t
μμ
∂
×× + ×× =
∂
∫∫∫ ∫∫∫
DD
I
rv vr
ωωω
(12.1.44')
takes place.
If, in particular, the frame
R does not rotate ( = 0ω , hence
OO
=KK too) or the
pole of the frame
R coincides with the mass centre (OC≡ , hence = 0
ρ
), then one
obtains again the formulae (11.2.19–11.2.21'); we remark, especially, the frames and
the formulae of Koenig type. Finally, if both conditions mentioned above hold
simultaneously, then the frame
R is a Koenig frame and Koenig’s theorems hold too.
For a subsystem
S ⊂ S
we can write the second theorem (11.2.22) in the form
()
() () () ()
dd()d
n
CC C C
VS V
t
μμ
∂
∂
×=×+×
∂
∫∫∫ ∫∫ ∫∫∫
DDD
rv rp rF, D∀⊂D ,
(12.1.45)
and may enounce (a principle equivalent to the principle iii
2
) or a theorem considered as
a consequence of the latter principle)
iii'
2
) Principle of variation of moment of momentum with respect to the centre
of mass.
The derivative with respect to time, in a Koenig frame of reference, of the
moment of momentum of any subsystem
S ⊂ S , in any configuration of it, with
respect to the mass centre, is equal to the moment of the forces which act upon that
subsystem, with respect to the same pole.
For the continuous mechanical system
S it results a formula of the form (11.2.24''),
so that we can state (second theorem of Koenig for the moment of momentum)
Theorem 12.1.10 (theorem of moment of momentum with respect to the centre of
mass). The derivative with respect to time, in a Koenig frame of reference, of the
moment of momentum of a continuous mechanical system subjected to constraints, with
respect to the centre of mass, is equal to the moment of the given and constraint
external forces, with respect to the same pole.
The theorem of momentum in the form (11.2.15) corresponds to the motion of the
centre of mass, while the theorem of moment of momentum in the form (11.2.24'')
describes the rotation of the continuous mechanical system about the centre of mass, the
privileged rôle of which is thus put in evidence.
As in Sect. 11.2.2.1, we can prove a formula of the form (11.2.23'); the Theorem
11.2.9 of C. Iacob can be thus stated for a continuous mechanical system too. As well,
99
12 Dynamics of Continuous Mechanical Systems

the theorem of moment of momentum will have, in general, the same form (11.2.24).
Obviously, in the particular cases
= 0ω or = 0
ρ
we obtain the same results.
We can introduce the dynamic resultant of the continuous mechanical system
S
d
(;) (;)d
d
ttV
t
μ
′′′′
∫∫∫
D
Arvr=
(12.1.46)
and the dynamic moment of the same system
d
(;) (;)d
d
O
ttV
t
μ
′
⎡⎤
′′′′′
×
⎢⎥
⎣⎦
∫∫∫
D
Drrvr= ,
(12.1.46')
obtaining the results expressed by the formulae (11.2.11') and (11.2.24–11.2.26').
Conservation theorems (hence, first integrals) can be obtained only with respect to
the inertial frame of reference
′
R
, in conditions analogous to those put in evidence in
Sect. 11.2.2.1.
The kinetic energy is defined in the form
2
1
d
2
TvV
μ
′′
=
∫∫∫
D
;
(12.1.47)
taking into account (12.1.40), (12.1.40'), we find again the formula (11.2.28) of the
kinetic energy, where the velocity
C
′
v is given by (11.2.14), the kinetic energy
T
with
respect to the frame
R
being expressed in the form
()
2
2
11d
()d d
22d
TVV
t
μμ=+×=
∫∫∫ ∫∫∫
DD
r
vr
ω .
(12.1.48)
Introducing the moment of momentum (12.1.43), we can express the kinetic energy
T
in the form (11.2.28''), where the kinetic energy of the continuous mechanical system
S
with respect to the non-inertial frame
R is given by
2
1
d
2
TvV
μ=
∫∫∫
D
.
(12.1.47')
The Theorem 11.2.10 of V. Vâlcovici can be thus stated also for a continuous
mechanical system
S ; as well, one can use also the formulae (11.2.29–11.2.30).
The elementary work and the power of the given and constraint, external and internal
forces may be further expressed by the formulae (11.2.31), (11.2.31'), so that the
Theorem 11.2.11 can be stated for a continuous mechanical system too. As a matter of
fact, assuming catastatic internal constraints, we have
int int
dd
RR
WW
′
=
int int
0
RR
PP
′
===, the elementary work of deformation being contained in
int
dW
′
and
int
dW (or in
int
P
′
and
int
P ), respectively; indeed, we can assume that the
mechanical system
S is formed by several continuous subsystems, being thus subjected
to internal constraints.
100
MECHANICAL SYSTEMS, CLASSICAL MODELS

The theorem of kinetic energy is written in the form (11.2.34), (11.2.34') or in the
form (11.2.34''). We notice that all the considerations made in Sect. 11.2.2.2, by
particularization, hold. The same observations can be made for the formulae (11.2.41–
11.2.42') and for the reciprocity relation (11.2.43) of C. Iacob.
A theorem of mechanical energy of a continuous mechanical system, free or
subjected to constraints, as well as a conservation theorem of that energy (hence, a
scalar first integral) may be obtained in conditions analogous to those of a discrete
mechanical system.
12.2. One-dimensional Continuous Mechanical Systems
A study of the motion of threads and straight bars is presented in this paragraph;
results concerning longitudinal and transverse vibrations are also included.
12.2.1 Motion of Threads
In what follows, one makes some general considerations on one-dimensional
continuous mechanical systems; results concerning the motion and the vibrations of
threads are then dealt with.
12.2.1.1 General Considerations
A one-dimensional continuous mechanical system
L is modelled as a material line
(a one-dimensional variety in the space
3
E , to which we associate a mass depending on
a single variable; see Chap. 1, Sect. 1.1.8 too). Let be a curve
C, the geometric support
of the mechanical system
L ; its linear density is given by
d
(;) 0
d
m
st
s
μ =>, ()mms= ,
(12.2.1)
s being the curvilinear co-ordinate along that curve (a possible dependence on time is
also put in evidence). Hence, the mass of
L is expressed in the form
1
0
()d ()d
P
CP
Mss ssμμ==
∫∫
,
(12.2.1')
0
P and
1
P being the extremities of the material line; if that line is homogeneous, then
we have
Mlμ= , constμ = , (12.2.1'')
where
l is its length. A material line can be a thread or, eventually, a bar (see Chap. 1,
Sect. 1.1.10 too). If
A is the area of the cross section (a finite area), then we can write
(;) (;)st tAμμ= r , where (;) 0tμ >r is the volume density; it is necessary that
(;) (1/ )tAμ = Or , because (;)stμ is a bounded function. The position of the mass
centre is given by
101
12 Dynamics of Continuous Mechanical Systems
1
0
11
()d ()d
P
CP
ss ss
MM
μμ==
∫∫
rrρ ,
(12.2.2)
with respect to an arbitrary pole
O.
We assume that at the moment
0
tt= the material line occupies the initial position
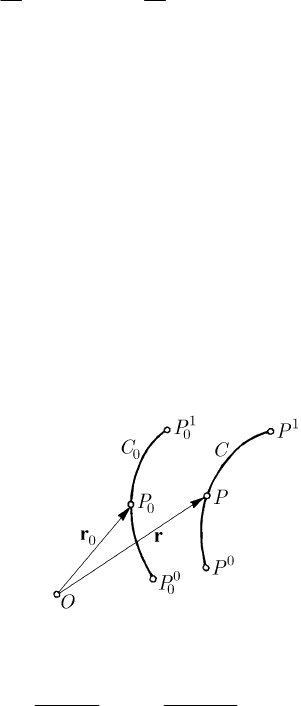
00
()Ct C= , while, at the moment t, the actual position is given by ()Ct C=
(Fig. 12.4). Introducing a parameter
[
]
01
,λλλ∈ , we can express the equation of the
curve
C occupied by the material line at the moment t in the form
(;)tλ=rr ;
(12.2.3)
for
0
tt= we obtain the curve
0
C , while
0
λλ= and
1
λλ= , respectively, specify the
extremities of the material line at an arbitrary given moment. The parameter λ plays
thus the rôle of a generalized co-ordinate. The velocity and the acceleration of a particle
in motion are given by (λ is fixed)
Fig. 12.4 Material line at the moment
0
t and at the moment t
(;)t
t
λ∂
=
∂
r
v
,
2
2
(;)t
t
λ∂
=
∂
r
a
.
(12.2.4)
For
t fixed, these formulae give the distribution of velocities and accelerations along the
curve
()Ct; in particular, for
0
tt=
are obtained the velocities and the accelerations at
the initial state (along the curve
0
C
)
00
(; ) ()tλλ=rr,
00
(; ) ()tλλ=vv,
00
(; ) ()tλλ=aa.
(12.2.4')
For the curvilinear integral
()
(;)d
Ct
C
IFts=
∫
r
(12.2.5)
one obtains the formula (A.2.82'), which can be written also in the form
102
MECHANICAL SYSTEMS, CLASSICAL MODELS
