Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

Passing from this piecewise continuous function to the corresponding regular

distribution, the formula (1.1.50) allows to write

()

∂∂



() ()

ut ut

δδ

∂∂

=+ +

∂∂





∂∂



;

observing that for

0t ≥ we have

∂





1,33

∂



the equation (12.2.25) may be written with the aid of regular distributions in the form

(assuming that

u ,

()uK

′

∈\, being thus distributions, we introduce the direct

product)

20 0

11,331 1

() ()ucu u tu tδδ=+×+×







(12.2.25')

the initial conditions being included too. We assume that the equation maintains its

form also if

u is a singular distribution; we apply the Fourier transform with respect to

the space variable (the regularity conditions at infinity are thus ensured, see App., Sect.

3.2.1) and the Laplace transform with respect to the time variable (see App., Sect.

3.2.2). We get

()

[][]

[

]

[

]

22 2 0 0

3111

LF F Fcp u u puα +=+ ,

wherefrom

[][]

[] []

()

111

22 2

LF F F

uupu



α and p being the new variables in the spaces of Fourier and Laplace transforms,

respectively. Taking into account the inverse Laplace transforms

22 2

sin

−

⎡⎤

⎢⎥

⎣⎦

22 2

Lcos

−

⎡⎤

⎢⎥

⎣⎦

we can write

[]

[] []

11 13

sin

FF Fcos

uu u ct

=+ ;

observing that

()

1222

sin

F()

tct x

θθ

−

⎡⎤

=−

⎢⎥

⎣⎦

[]

()

1222

333

Fcosct x x c tαδ

−

=−,

113

12 Dynamics of Continuous Mechanical Systems

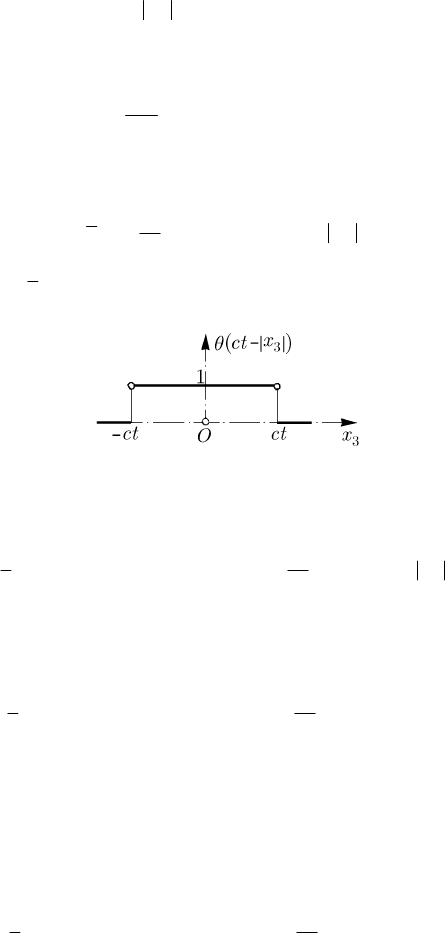
where

()

()()()

22 2

3333

ct x ct x x ct x ctθθθθ−= − = +− −,

0c >

is a distribution corresponding to a characteristic function of interval (Fig. 12.9), while

()

()()

[]

222

333

xct xct xct

δδδ−=− +−−

, 0c > ,

and using the formula (A.3.15), we get

[]

()

[]

11 3

FF()

uutctx

θθ=∗−



()

[]

()

[]

()

13 13

uxct uxctδδ+∗++∗−

Fig. 12.9 Characteristic function of interval

By means of the formula (A.3.6'), it results, finally,

()()

[]

()

00 0

13 13 13 1 3

(;)

uxt u x ct u x ct u ct x

θ=++−+∗−

 .

(12.2.27)

()ux C∈ ,

()ux C∈



, then we write the solution of Cauchy’s problem

corresponding to the equation (12.2.25) in the form

()()

[]

00 0

13 1 3 1 3 1

(;) ()d

xct

uxt u x ct u x ct u

ξξ

−

=++−+

∫

 ,

(12.2.27')

obtaining thus d’Alembert’s formula. Denoting

() ()d

sz u ξξ=

∫



(12.2.28)

we may also write

()()

[]

()()

[]

13 13 13 3 3

(;)

uxt uxctuxct sxctsxct

=++−++−−

(12.2.28')

putting thus in evidence the symmetric and the antisymmetric parts of the deformed

thread with respect to the origin

0x = , respectively; an initial deformation of the

114

MECHANICAL SYSTEMS, CLASSICAL MODELS

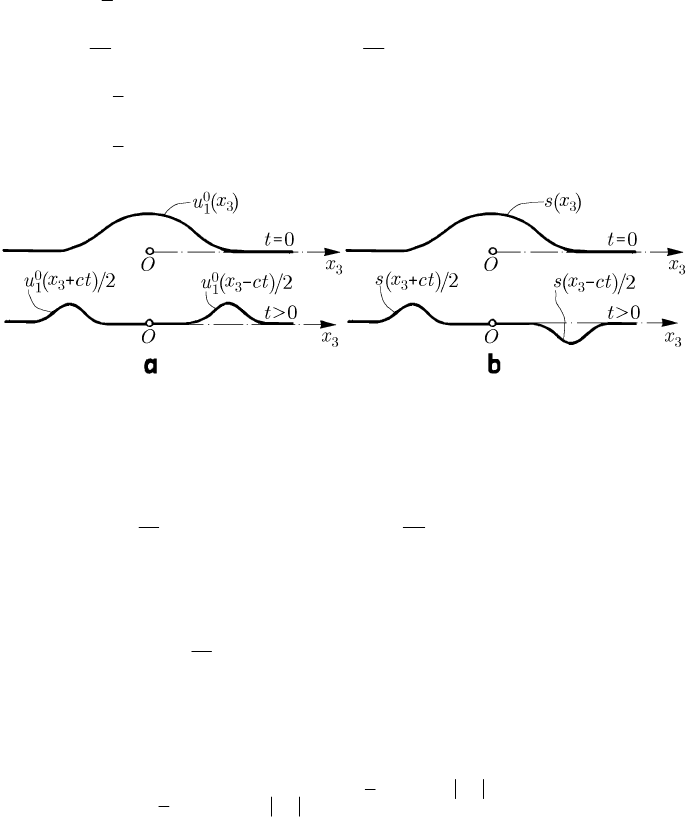
thread (a “crest”) given by

()ux (Fig. 12.10a) will be symmetrically propagated with

the propagation speed

c, while a deformation

()sx corresponding to the deformation

velocity (Fig. 12.10b) will be antisymmetrically propagated, with the same propagation

velocity

c (the “wave” advances by c in a unity of time).

In case of a semi-infinite thread, we put the condition at finite distance

(0; ) 0ut=

being thus led to the solution

()()()()()

[]

000

13 1 3 3 1 3 3 1 3

(;)

u x t u x ct x ct u x ct ct x u ct xθθ=++− −−− −

()()

[]

()()

[]

33 33

sx ct sx ct sx ct sx ct

+ +−−= +−−

()()

[]

()()

[]

13 1 3 3

13 13 3

for ,

for .

ux ct uctx x ct

ux ct ux ct x ct

⎧

+− − <

⎪

⎨

⎪

++ − >

⎩

(12.2.29)

Fig. 12.10 Deformed configuration of the thread: symmetric propagation (a);

antisymmetric propagation (b)

If a perturbing force

113

(;)ppxt= intervenes too, the equation of motion becomes

1,33 1 3

(;)uufxt

−=

 ,

313

(;) (;)

xt pxt

=− .

(12.2.30)

The solution

(;)EExt= of the equation

,33 3 3

(;) () ()EExtxt

δδδ−= = ×



(12.2.30')

is the fundamental solution in the sense of the theory of distributions of the equation

(12.2.30). Using the method of integral transforms, we get

()

for ,

(;) ()

0 otherwise;

xct

Ex t t ct x

θθ

⎧

−≤

⎪

=− − =

⎨

⎪

⎩

(12.2.30'')

115

12 Dynamics of Continuous Mechanical Systems

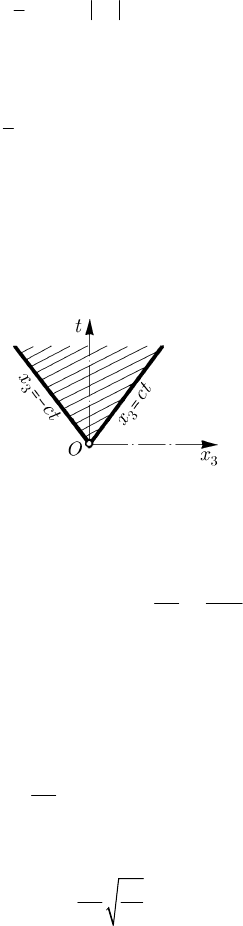
the fundamental solution is equal to

/2c− in the hatched zone and equal to zero in the

exterior of it (Fig. 12.11). The corresponding solution of the equation (12.2.30) reads

()

13 3 3

(;) (;)

uxt ct x fxtθ=− − ∗ ;

(12.2.31)

C∈ , then we can write

()

0()

(;) (,)dd

txct

xct

uxt f

ξτ ξτ

+−

−−

=−

∫∫

(12.2.31')

If the thread has a finite length, then we put boundary conditions of the form

(12.2.23), (12.2.23'). In case of steady-state vibrations, we assume that (we can obtain

separately solutions in

cos tω or in sin tω )

13 3

(;) ()e

uxt ux

= ,

ecosisin

ωω=+ , 0ω > ,

(12.2.32)

Fig. 12.11 Fundamental solution for the forced transverse vibrations of a thread

where

i is the imaginary unity; replacing in the equation (12.2.31), we find the equation

,33

0uuα+=,

μω

== ,

whose general integral is

333

() cos sinux A x B xαα=+. Putting the bilocal

conditions (12.2.23) (we cannot put initial conditions, because the vibrations are

stationary), we get

0A = and 0B ≠ , with the characteristic equation sin 0lα = ,

which leads to the eigenvalues

= , n ∈ ` ,

(12.2.33)

and then to the proper pulsations (circular frequencies)

ωα

== ;

(12.2.33')

the proper form of the free vibrations is thus given by

13 3

(;) e sin

uxt B x

α=

, n ∈ ` .

(12.2.33'')

116

MECHANICAL SYSTEMS, CLASSICAL MODELS

We see that

13 13

(;)(;)

ux t uxtλ+= for 2lλ = ; λ is called wave length. As well,

13 13

(; ) (;)

uxt uxtτ+= for the period 2/ /

ncτπωλ==, where c is the

propagation velocity of the wave. We notice that the transverse displacement

(;)

uxt vanishes for

//2xklnknλ== , 0,1,2,...,kn= , the vibrations of the

thread having thus

n–1 nodes between the fixed extremities. The frequency of the

vibrations (the number

of vibrations in a unity of time) is given by

1/ /

ncτλ==, defining thus the height of the tone emitted by the wave

(important, e.g., in acoustics); for

1n = one obtains the fundamental tone, while for

2n = we have the octave of the fundamental tone.

In case of forced vibrations, due to the perturbing force

13 3

(;) ()e

pxt px

= , 0ω > ,

(12.2.32')

the equation (12.2.30) reads

0,33

0Tu u pμω++=.

Applying the sinus Fourier transform and observing that

,33 3 3 ,3 3 3 3 3

0 0

sin d sin cos sin d

l l

nnnnnn

uxxuxux uxxαααααα=− −

∫∫

sin d F [ ]

nn ns

uxx uαα α=− =−

∫

because

(0) ( ) 0uul== and sin 0 sin 0

lαα==, we get

()

F[ ] F[ ] 0

sn s

uT pαμω−−+=,

so that (we use the proper pulsation (12.2.33'))

[]

F[ ]

1(/ )

αωω

−

;

effecting the inverse Fourier transform, it results

[]

sin

(;) e ()sin d

1(/ )

uxt p

ξαξξ

αωω

∞

−

∑

∫

(12.2.34)

We notice that a phenomenon of resonance can take place if the pulsation

ω of the

forced vibrations is very close to one of the proper pulsations

ω (the displacement

tends to infinity and the stability is lost by divergence); it is true that, in this case, the

hypothesis of small displacements with respect to the length of the thread does no more

hold. In case of the action of a concentrated force

13 3

(;) e ( )

pxt x

δξ=− at the

point

x ξ= , we notice that, by abuse of notation, we can write

117

12 Dynamics of Continuous Mechanical Systems

333

()sindsin

xxxδξα αξ−=

∫

so that we obtain Green’s function of the equation (12.2.30) in the form

[]

13 3

sin sin

(;) e (,;)

1(/ )

uxt Gx t

ααξ

αωω

∞

−

∑

(12.2.35)

corresponding to a line of influence for the thread. We notice the relation

(,;) (,;)Gx t G x tξξ= ,

(12.2.35')

that is a reciprocity theorem of Betti type (the displacement at the point

x , due to a

unitary concentrated force applied at

ξ, is equal to the displacement at ξ, due to a

unitary concentrated force applied at

x ). In this case, we obtain

13 3

(;) ()(,;)d

uxt p Gx tξξξ=

∫

(12.2.35'')

for an arbitrary load (12.2.32'). We can express Green’s function also in a finite form by

the relation (expanding this relation into a Fourier series, we get (12.2.35))

sin sin ( ) for 0 ,

(,;)

sin

sin sin ( ) for .

xl x

Gx t

lx x l

ααξ ξ

αα

αξ α ξ

−<<

⎧

⎪

⎨

−<<

⎪

⎩

(12.2.35''')

If the vibrations are arbitrary (non-stationary), we impose the initial conditions

(12.2.23') too. Effecting a Laplace transform and a finite sinus Fourier transform on the

equation (12.2.25), brought to the form (12.2.25') in distributions, we get

[][]

[] []

()

111

222

FL F F

sss

uupu

 ;

using the same method of computation, it results, finally,

13 1 1 3

2sin

( ;) cos ()sin d ()sin d sin

nn nn

uxt t u u x

ω ξ αξ ξ ξ αξ ξ α

∞

⎡⎤

⎢⎥

⎣⎦

∑

∫∫



(12.2.36)

with the notations (12.2.33), (12.2.33').

Taking into account the action of a perturbing force

113

(;)ppxt= , we apply,

analogously, the Laplace transform and the finite sinus Fourier transform to the

equation (12.2.30); neglecting the influence of the initial conditions (homogeneous

initial conditions), we obtain

[][]

()

[][]

222

FL FL

μα

118

MECHANICAL SYSTEMS, CLASSICAL MODELS

wherefrom, using the convolution theorem, we get

13 1

sin

(;) sin d (;)sin ( )d

uxt p t

αξ ξ ξτ ω τ τ

∞

=−

∑

∫∫

(12.2.36')

If the thread is acted upon by a concentrated unitary force at the initial moment (a

shock), at the point

x ξ= , we can write

13 3

(;) ( ) ()pxt x tδξδ=−×, obtaining the

corresponding Green function

sin

( , ;) sin sin () (, ;)

sin

Gx t t G x t

ξαξωξ

∞

∑

(12.2.37)

so that, for an arbitrary load

(;)pxt C∈ , it results

13 3 1

(;) d (,; )(;)d

uxt Gx t pξξτξττ=−

∫∫

(12.2.37')

12.2.2 Motion of a Straight Bar

The straight bar is a rectilinear one-dimensional continuous mechanical system for

which, in the computation of the momentum

H and of the moment of momentum

one must take into account the cross section of area

A. In what follows, we present

some results concerning the motion and the vibrations of a straight bar.

12.2.2.1 Equations of Motion of a Straight Bar

Assuming that the linear unit mass

μ is constant on the cross section of area A (it does

not depend on the position vector

r situated in the plane of that section and having the

origin on the bar axis), we can write (

ddsx= )

=(,;)dd

tA x

μλ

′′

′

⎡⎤

⎣⎦

∫∫

Hvr,

=() (,;)dd

tA x

μλ

′′

′

⎡⎤

+×

⎣⎦

∫∫

Krrvr .

Proceeding as in Sect. 12.2.1.1 and observing that (

()/t∂+ ∂=rr v)

()d d d

AAA

∂∂

+× −× = ×

∂∂

∫∫∫

rr v r v ra ,

we obtain the equations

ddd

AAA

At A A

μμμ

∂

+= = =

∂

∫∫∫

Rp v a u,

(12.2.38)

,3 3

μμ

+×+= × = ×

∫∫

Mirm ra ru,

(12.2.38')

119

12 Dynamics of Continuous Mechanical Systems

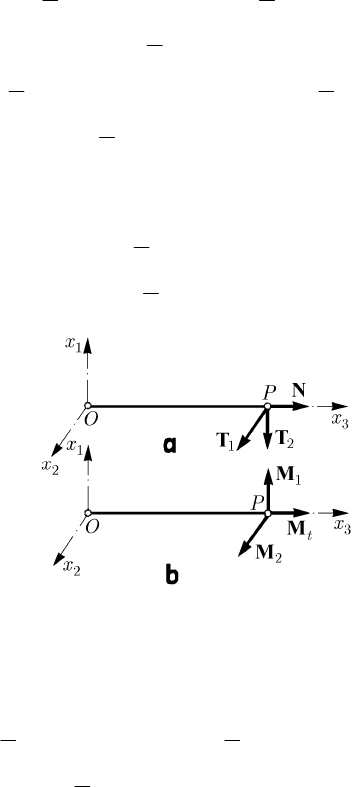
where we have used an orthonormed right-handed fixed frame

123

Ox x x , the

Ox -axis

being along the bar axis, and where we took into account the displacement acceleration

(12.1.3'). In the frame of the notation convention used in technical mechanics of

deformable solids, the components of the torsor of internal forces (the efforts on the

cross section) are given by (4.2.41) and the external load is expressed in the form

(4.2.41') (Fig. 12.12ab); there results the relations (the rectilinear continuous

mechanical system is flexible, torsionable and extensible)

2,3 1 1

Tp uA

−+=

∫

 ,

1,3 2 2

Tp uA

∫

 ,

1,3 3 3

Np uA

∫



(12.2.39)

1,3 1 1 2 3

MTm xuA

−+ =

∫

 ,

2,3 2 2 1 3

MTm xuA

−+ =−

∫

 ,

()

,3 3 1 2 2 1

Mm xuxuA

+= −

∫

  .

(12.2.39')

Eliminating the shearing forces, we get

()

1,33 1,3 2 2 2 3,3

Mmp uxuA

++= +

∫

  ,

()

2,33 2,3 1 1 1 3,3

Mmp uxuA

+−=− +

∫

  .

(12.2.40)

Fig. 12.12 Efforts on a cross section of a straight bar: forces (a), moments (b)

In case of external loads contained in the plane

Ox x

we have

0p =

0mm==

; it results

1,3 2

TuA

∫



1,3 1 2 3

MT xuA

∫



()

,3 1 2 2 1

MxuxuA

=−

∫

  ,

(12.2.41)

wherefrom, integrating with respect to

x , we obtain, successively, the efforts

and

M . If we have

0m =

too, then the other relations can be written in the form

120

MECHANICAL SYSTEMS, CLASSICAL MODELS

2,3 1 1

Tp uA

=−

∫



,3 3 3

Np uA

=− +

∫



2,3 2 1 3

MT xuA

=−

∫

 ,

(12.2.41')

wherefrom

()

2,33 1 1 1 3,3

Mp uxuA

=− +

∫

 

(12.2.41'')

2.2.2 Longitudinal and Torsional Vibrations of a Straight Bar

If the efforts on the cross section are reduced to the axial force

N, we are in the

particular case in which

0pp==,

123

0mmm===; the components of the

displacement vector are

0uu==,

3312

(, ;)uuxxt= . The equations (12.2.39),

(12.2.39') are reduced to the second equation (12.2.41'), the other equations being

identically verified; observing that the axial force is given by

33 33 3,3

NA AE EAuσε== = , where EA is the rigidity by axial efforts, this equation

takes the form (12.2.10') or the form

3,33 3

0uu

−=

= ,

(12.2.42)

corresponding to the equation (12.2.15), in the absence of the perturbing force. We can

thus state that the longitudinal vibrations of the straight bar are governed by the same

partial derivative equations as the longitudinal vibrations of threads.

The solutions of the boundary value problem depend on the conditions on the end

cross sections of the bar (bilocal conditions) and on the initial conditions. Thus, in case

of a bar of infinite length with initial conditions (12.2.21') for

(,)x ∈−∞∞, we find

[]

00 0

33 33 33 3

(;) ( ) ( ) ()d

xct

uxt ux ct ux ct u

ξξ

−

=++−+

∫

 .

(12.2.42')

In case of free longitudinal vibrations of a simply supported bar of finite length

hence for which the bilocal conditions (12.2.21) are put, we impose the same initial

conditions (12.2.21'); we obtain thus

33 3 3 3

2sin

( ; ) sin cos ( )sin d ( )sin d

nn n n

uxt x t u u

α ω ξαξξ ξαξξ

∞

⎡

⎤

⎢

⎥

⎣

⎦

∑

∫∫

 ,

(12.2.43)

with the proper pulsations

nEA

ωα

== ,

= ,

(12.2.43')

121

12 Dynamics of Continuous Mechanical Systems

corresponding to the formula (12.2.36). For the forced vibrations of the bar, due to the

perturbing force

333

(;)ppxt= , the formula (12.2.36') allows to write

33 3

sin

(;) sin d (;)sin ( )d

uxt p t

EA l

αξ ξ ξτ ω τ τ

∞

=−

∑

∫∫

;

(12.2.43'')

in particular, in case of the perturbing force

33 3

(;) ()e

pxt px

= , 0ω > , it results

[]

sin

(;) e ()sin d

1(/ )

uxt p

EAl

ξαξξ

αωω

∞

−

∑

∫

(12.2.43''')

corresponding to the formula (12.2.34). In case of other types of supports, the

corresponding boundary conditions are modified; e.g., if the right end cross section

(

xl=

) is free, then the normal stress

σ must vanish, i.e.

3,3

(;) 0ult= ,

tt≥ ,

(12.2.44)

taking into account Hooke’s law.

In case of a phenomenon of torsion, the moment of torsion is given by

MGIθ= ,

where

GI is the torsional rigidity (G is the modulus of transverse elasticity and

I is

the moment of inertia by torsion, which is reduced to the polar moment of inertia

I in

case of a circular or annular cross section), while

θϑ= is the angle of unit rotation

(

is the rotation angle); one can show that

uxϑ=−

uxϑ=

, so that from the

third equation (12.2.39') we obtain the equation of free torsional vibrations of the

straight bar in the form

,33 3

GI m I

ϑϑ



(12.2.45)

where

I is the polar moment of inertia of the cross section. This equation is of the

same form as the equation of longitudinal vibrations of the bar. In the absence of the

perturbing moment

m , the homogeneous equation (12.2.45) can be written in the form

,33

ϑϑ−=



= ,

(12.2.45')

where

GA is the shearing rigidity. If the left end cross section of the bar is built-in, the

condition

(0; ) 0tϑ =

(12.2.46)

is imposed, while if it is free one must have

(0; ) 0tϑ =

;

(12.2.46')

122

MECHANICAL SYSTEMS, CLASSICAL MODELS