Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

()

sF s

λλ

∂∂

⋅

∂∂

∂

∫∫

(12.2.5')

The principle of mass conservation is written in the form (the material line

′′′

is a

subsystem of the continuous mechanical system

PP, its extremities being specified

by the values

′

and λ

′′

of the parameter λ)

00 0

(;)d ( ; )dst s s t s

λλ

μμ

′′ ′′

′′

∫∫

where the elements of arc are given by

dds λ

∂

dds λ

∂

;

(12.2.3')

the relation must take place for any

′

and

′′

, so that one obtains the continuity

condition of d’Alembert in the form

(;) ()tμλ μ λ

λλ

∂

∂∂

() (; )tμλ μλ=

(12.2.6)

or in the form

(;)d ( )dst s s sμμ= ,

000

() (;)sstμμ= .

(12.2.6')

One can write this principle in the form

(;)d 0

st s

′′

′

∫

too; applying the formula (12.2.5') and noting that the limits

′

and

′′

are arbitrary, it

results the condition of continuity

()

(;)

(;) 0

μλ

λλλ

∂

∂∂∂

+⋅=

∂∂ ∂∂

rrv

(12.2.6'')

corresponding to the continuity condition of Euler (1.1.79). These conditions of

continuity are, obviously, equivalent.

Taking

(;) (;)(;)Ft t tΦλ μλ=r , applying the formula (12.2.5') and taking into

account (12.2.6''), we get

(;)(;)d d

tts s

Φλ μλ μ

∂

∫∫

;

(12.2.7)

103

12 Dynamics of Continuous Mechanical Systems

analogously, we have

(;)(;)d d

tts s

Φμλ μ

∂

∫∫

r ,

(12.2.7')

as well as

(;)(;)d d

tts s

μλ μ

∂

∫∫

Ψ ,

(12.2.7'')

(;)(;)d d

tts s

λμλ μ

∂

∫∫

(12.2.7''')

Upon the material arc

′′′

in the actual state (at the moment t) there are exerted

actions at distance (volume forces

()dsλp and volume moments ()dsλm ; in case of

deformable solids it is convenient to report these quantities to the unity of volume) on

all its length and actions of contact (the resultants

()λ

′

−R and ()λ

′′

R and the

resultant moments

()λ

′

−M and ()λ

′′

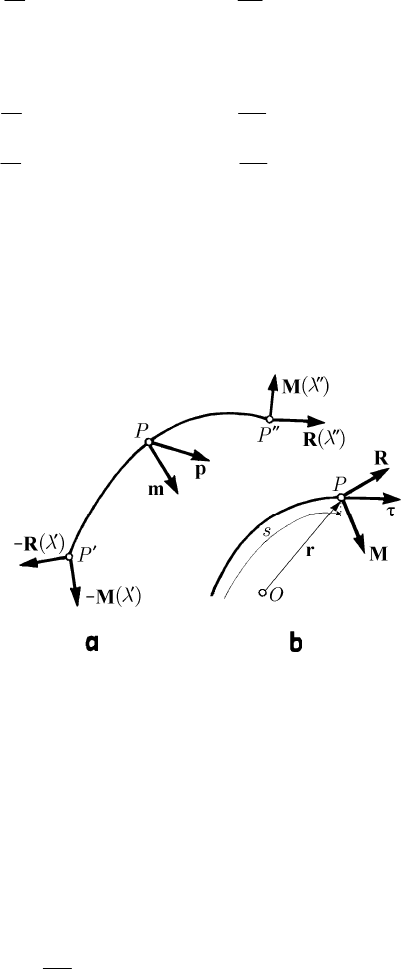
M ) at its extremities (Fig. 12.5a).

Fig. 12.5 Dynamic equilibrium of a material arc

′′′

PP (a).

Efforts on a cross section (b)

The momentum and the moment of momentum with respect to a fixed pole

O are

given by

′′

′

∫

Hv(;)dts

μλ

[]

′′

′

=×

∫

Krv(;)d

μλ

The principle of variation of momentum and the principle of variation of moment of

momentum allow to write

′′

′

′′ ′

=+−

∫

pRR

()d ( ) ( )

λλλ,

104

MECHANICAL SYSTEMS, CLASSICAL MODELS

′′

′

′′ ′′ ′ ′

=×+×−×

∫

rp r R r R

() ()d ( ) ( ) ( ) ( )

λλ λ λ λ λ

′′

′

′′ ′

++−

∫

mMM()d ( ) ( )s

λλλ.

Eventual concentrated forces or moments acting along the material arc

′′′

can be

contained in

()dsλp and ()dsλm ; but these quantities must be, in this case,

represented by distributions. Taking into account (12.2.7''') and observing that

() () d

λλ λ

′′

′

∂

′′ ′

−=

∂

∫

() () d

λλ λ

′′

′

∂

′′ ′

−=

∂

∫

() () () () ( )d

λλλλ λ

′′

′

∂

′′ ′′ ′ ′

×−×= ×

∂

∫

rRrR rR,

we obtain

()

d0s

′′

′

∂∂∂

−− =

∂∂∂

∫

()

() () d0

tss

λλ

μλ

λλ

′′

′

∂∂ ∂

⎡⎤

×−−× −− =

⎢⎥

∂∂ ∂

⎣⎦

∫

rprRm

Because the limits

′

and λ

′′

are arbitrary, we can write

μμ

∂∂

+= =

∂∂

(12.2.8)

as well as

()

tss s

∂∂∂ ∂

×−−−×−−=

∂∂∂ ∂

vRr M

rp Rm0

;

taking into account (12.2.8), we get the second equation of motion (

/ s=∂ ∂rτ is the

unit vector of the tangent to the material curve

()Ct (Fig.12.5b))

∂

+× + =

∂

Rm0τ

(12.2.8')

In the static case, we find again the equations (4.2.36) corresponding to a curved bar

(one-dimensional continuous mechanical system). We notice that, in the dynamic case,

we use the partial derivative with respect to the curvilinear co-ordinate

s, because the

considered quantities depend on the temporal variable

t too, e.g., (;)st=rr . The

condition of continuity (12.2.6'') must also be associated to these equations.

105

12 Dynamics of Continuous Mechanical Systems

12.2.1.2 Equations of Motion of Threads

A thread will be modelled by its axis; thus, the points of application of the external

forces as well as those of the efforts are situated on the same axis. If, in the equations of

motion (12.2.8), (12.2.8'), we neglect the concentrated moments

M and the external

loads given by distributed moments

m (the thread being perfect flexible and

torsionable), then we can express these equations in the form

(;)

(;) (;)

st st

∂

∂∂

, (;) (;)st st×=R0τ ,

(12.2.9)

where

(;)stp is the external load (distributed on the unit length of the thread), applied

at the point of curvilinear abscissa

s at the moment t, while (;)stR is the resultant of

the efforts on the corresponding cross section. Taking into account the second equation

(12.2.9) (corresponding to the chosen model for the thread),

(;)stR is reduced to the

axial force

(;)stT of traction (the tension (;)stT along the direction of the unit vector

τ, tangent to the thread (see Fig. 4.47 too)) and we can state

Theorem 12.2.1 At any point of a perfect flexible and torsionable thread, in any of its

configurations, the tension is tangent to the curve occupied by the thread.

The equation of motion is reduced to

(;)

(;) (;)

st st

∂

∂∂

(12.2.10)

Noting that

(;) (;)(;)st T st st=T τ , (;) 0Tst ≥ , is the tension in the thread at the

cross section of curvilinear co-ordinate

s, it results

(;)

(;) (;) (;)

Tst st st

ss t

∂

∂∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

;

(12.2.10')

in Frenet’s frame, the equations have the form

∂



ρρ

, 0p

= .

(12.2.10'')

The third equation (12.2.10'') shows that, to have dynamic equilibrium at any point of

the thread, the external force

p must be contained in the corresponding osculating plane

(in other words, the osculating plane to the deformed configuration of the thread

contains, at any moment, the support of the external force

p).

Finally, the equations

λλ

∂

⎛⎞

⎜⎟

∂∂

∂

⎜⎟

∂∂

∂

⎜⎟

∂∂

⎝⎠

(12.2.11)

106

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

λλλ

∂

∂∂∂

+⋅ =

∂∂ ∂ ∂∂

rrr

(12.2.11')

constitute a system of four scalar equations with partial derivatives for five unknown

functions:

(;)TT tλ= , (;)tμμλ= and (;)

xxtλ= ,

1,2, 3

i =

. To solve the

problem, it is necessary to associate a fifth equation, corresponding to the constitutive

law of the material.

The curvilinear abscissa of the particle individualized by the parameter

λ on the

curve

()Ct at the moment t is given by

(;) dst

λλ

∂

∫

;

at the same moment

t, we have

(;)

∂

while for the moment

dtt+ we can write

(; d) (;)

ddddd

tt t

sst

λλ

∂+ ∂

∂

′

==+

∂∂∂

neglecting the terms of higher order. The variation of the linear strain in the time

interval d

t is written in the form

(;)

dd d

(;)

st s

∂

∂∂

∂

′

−∂

∂∂

∂

The velocity of strain is given by (

(;)tεελ= is the linear strain; see the formula

(12.1.30'))

() ()

tλλ λλ

λλ

∂∂ ∂∂

⋅⋅

∂∂∂ ∂∂

∂∂



rr rv

;

(12.2.12)

in this case, the condition of continuity (12.2.11') can be written in the form

0μμε+=



, (12.2.12')

so that

107

12 Dynamics of Continuous Mechanical Systems

ln Cεμ+=, e C

μ = ,

(12.2.12'')

where

,CC are constant with respect to time. An elastic constitutive law is of the form

()TTε= ;

(12.2.13)

in particular, if

Tkε= , constk = , (12.2.13')

then the constitutive law is linearly elastic.

In the case in which

0ε =



, hence if ε is constant in time (the tension T has the same

property), then from (12.2.12') it results

(;) (; ) ()ttμλ μλ μλ== too, the thread

being, in general, non-homogeneous; if the thread is homogeneous, then we have

() () constμλ μ λ==. From (12.2.1) one obtains

(;)

const

tλ

∂

(12.2.14)

If in the motion of the thread we have

(;) (; ) ()st st sλλ λ==, then we can take as

parameter on the curve

()Ct the curvilinear abscissa s (instead of λ). If, in particular,

0ε = , then the thread is inextensible.

The motion of a perfect flexible and torsionable thread is thus governed by the

equation (taking into account (12.1.3'))

()

(;)

()

sss

∂

∂∂∂

=+ =+

∂∂∂

∂

(12.2.15)

which, in projection on the three co-ordinate axes, leads to

(;) (;)

()

ust xst

spT

∂∂

∂

⎛⎞

⎜⎟

∂∂

∂

⎝⎠

, 1, 2,3i = .

(12.2.15')

To this equation is associated the condition of continuity, which, for

0ε =

, is of the

form

(;)

∂

(12.2.15'')

One can thus determine the four unknown functions

(;)TTst= and (;)

xxst= ,

1,2, 3

i = ; the linear density is, in this case, a given function.

If the thread is subjected to constraints, the influence of the constraint forces is added

too; if the thread is constrained to stay on a surface, then to the distributed force

p is

added a distributed constraint force

R, which must be determined. In Chap. 4,

108

MECHANICAL SYSTEMS, CLASSICAL MODELS

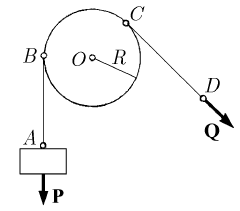
Sect. 2.2.4 one has considered the static problem of a thread constrained to stay on a

surface, in particular the case in which the thread is situated along the directrix of a

circular cylinder; thus, one can change the direction of a force (Fig. 12.6). As well, a

weight

P can be raised by means of a force Q, so that, in the absence of friction,

QP= (see also the static problem of the pulley in Chap. 4, Sect. 2.1.6); but if the

phenomenon of friction appears too, it is possible to be necessary a force

Q for which

QP

(see Chap. 4, Sect. 2.2.4). In this case, one uses a pulley, hence a cylinder

movable around a horizontal axle. Due to friction, the (perfect flexible) thread abuts on

the cylinder along

BC, moving as a rigid (Fig. 12.6). We assume that the forces P and

Q, applied at A and D, respectively, are constant as direction, the angle

BOC being

constant during the motion of the thread (the thread is inextensible and does not slide on

the pulley). We neglect the rolling friction in the bearing of the axle through

O, the

normal constraint forces leading to a vanishing moment with respect to that point. The

velocity of a point of the thread is

Rω, where ω is the angular velocity of rotation; if μ

is the density of the thread, then its moment of momentum is

Fig. 12.6 Change of direction of a force with the aid of a pulley

()

ddd

AB BC CD

rsssrmωμ μ μω++ =

∫∫∫

where

m is the mass. Applying the theorem of moment of momentum to the system

pulley-thread, we can write

()

Imr QPrω+=−



(12.2.16)

where

is the moment of inertia of the pulley with respect to the axis passing through

O. Neglecting the mass of the thread and its moment of inertia with respect to

I , it

results, with a good approximation,

()

IQPrω =−



(12.2.16')

In case of equilibrium (

0ω = ) or in case of a uniform motion ( 0ω =



) we get QP= ;

we obtain the same result if we assume that also the pulley has a negligible mass, hence

that the moment of inertia

is very small. The pulley allows thus to change the

109

12 Dynamics of Continuous Mechanical Systems

direction of a force, modifying only a little its intensity. As an illustration of those

results, we mention the Atwood engine, which was considered in Sect. 11.1.2.2.

For a complete formulation of the boundary value problem, one must give also the

initial conditions and the conditions on the frontier. Thus, the initial conditions (at the

moment

tt= ) are, in general, of the form

(; ) ()st s=rr,

(;)

()

∂

[

]

,sss∈ ,

(12.2.17)

specifying the position of the thread and the repartition of the velocities at that moment.

In case of a thread of finite length, the conditions on the contour are bilocal conditions.

For instance, one can give the position vectors

(;) ()st t=rr,

[

]

,ttt∈ ,

(12.2.18)

or the velocities

(;) ()st t=



rr,

(;) ()st t=



rr,

[

]

,ttt∈ ,

(12.2.18')

at the extremities of the thread; eventually, one can put mixed bilocal conditions

(position vector at one extremity and velocity at the other extremity) or one extremity or

two extremities can be fixed. As well, one can give the external forces which act at

those points

(;) ()st t−=TF,

(;) ()st t=TF,

[

]

,ttt∈ .

(12.2.18'')

In the absence of the force

p, assuming that

() (;)/ 0ssttμ ∂∂≅u , the equation

(12.2.15) takes the form

(;) ()st t=TC, (;) ()Tst Tt= , so that / s∂∂r

()/ ()tTt= C , () 0Tt ≠ ; thus, it results

()

(;) ()

()

st s t

(12.2.19)

() 0Tt ≡ , then the thread can take any form at the moment t.

12.2.1.3 Longitudinal and Transverse Vibrations of Threads

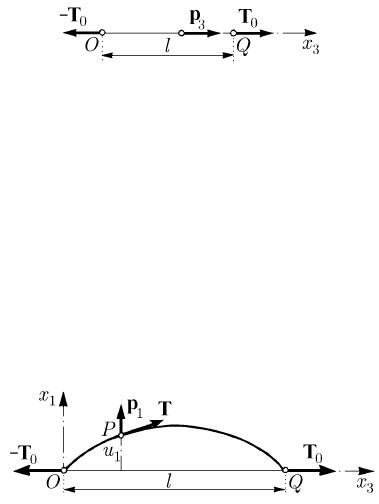
Let be a thread stretched between two points

O and Q at a distance l, along the

axis, by the action of a static tension

T ; we assume that the thread is acted upon by a

longitudinal force

p too, of intensity

333

(;)ppxt= (Fig. 12.7). Making 3i = in the

equation (12.2.15') and observing that

sx= , we obtain

,3 3 3

Tp uμ+= . (12.2.20)

110

MECHANICAL SYSTEMS, CLASSICAL MODELS

The tension in the thread is given by

033

TT Aσ=+ , where A is the area of the cross

section, while the normal stress

σ is linked to the linear strain

ε by Hooke’s linear

constitutive law

33 33

Eσε= , where E is the modulus of longitudinal elasticity; we find

thus a linear elastic constitutive law

033

TT EAε=+ , where EA is the rigidity in

traction (longitudinal effort). Taking into account Cauchy’s relation

33 3,3

uε =

(corresponding to (12.1.30')), the equation (12.2.20) of longitudinal vibrations of

threads takes the form

3,33 3 3

EAu p uμ+=



(12.2.20')

where the unknown function

333

(;)uuxt= is the displacement component along the

Ox -axis. The boundary conditions are conditions on the contour and initial conditions.

In our case, the conditions on the contour are bilocal conditions of the form (thread with

fixed extremities)

Fig. 12.7 Longitudinal vibrations of threads

(0; ) ( ; ) 0utult==,

tt≥ ,

(12.2.21)

while the initial conditions are of Cauchy type

33 33

(;0) ()ux ux= ,

33 33

(;0) ()ux ux=



(12.2.21')

for

[

]

0,xl∈ . In case of a thread of infinite length, we put analogous conditions at

infinity, the initial conditions being of the same form for

x−∞ < < ∞ . Obviously, we

can imagine also other bilocal conditions for a thread of finite length (e.g., imposed

displacements or given tensions, depending on time).

Fig. 12.8 Transverse vibrations of threads

Let us consider also a thread stretched between the points

O and Q by the action of a

static tension

T , acted upon by a transverse force

p , of intensity

(;)pxt, in the

plane

Ox x (Fig. 12.8); in this case, taking into account that the force

p must be

contained at each point of the thread in the osculating plane, it results that the actual

configuration of the thread is contained in the same plane. The relation (12.1.3) allows

111

12 Dynamics of Continuous Mechanical Systems

to write

111

xxu=+, where

113

(;)uuxt= is the displacement component along the

direction of the

Ox -axis; because

0x = , corresponding to a point of the non-

deformed thread (along the

Ox -axis), it results

xu= . The equation (12.2.15') is

thus written in the form

Tpu

∂

⎛⎞

⎜⎟

∂∂

⎝⎠



(12.2.22)

for

1i =

. Taking into account the relation

330

/Tx s T T∂∂==, as well as

/1xs∂∂≅ in case of small deformations, we can assume that

constTT≅=

; on

the other hand, we notice that

()( )

33 3

// //sxxsx∂∂=∂∂ ∂ ∂ ≅∂∂ , according to the

same linear approximation. The equation (12.2.22) of the transverse vibrations of

threads will be of the form

01,33 1 1

Tu p uμ+= . (12.2.22')

The contour (bilocal) conditions are, in general, of the form

(0; ) ( ; ) 0utult==,

tt≥ ,

(12.2.23)

while the initial conditions (of Cauchy type) read

13 1 3

(;0) ()ux u x= ,

13 1 3

(;0) ()ux u x=



[

]

0,xl∈ .

(12.2.23')

As well, we can write the transverse vibrations equation of threads in the plane

Ox x

in the form

02,33 2 2

Tu p uμ+= , (12.2.24)

and the boundary conditions are analogously put.

We notice that the equations (12.2.20') and (12.2.22') have the same form. Referring,

for instance, only to the equation (12.2.22') we obtain, in absence of external forces,

d’Alembert’s equation of the vibrating string (the homogeneous equation)

1,33 1

−=

 ,

= .

(12.2.25)

We assume firstly that the thread is of infinite length, the initial conditions being of

the form (12.2.23') for

x−∞ < < ∞ . By means of Heaviside’s function ()tθ , we

introduce the positive part of the function

(;)uxt in the form

13 13

0 for 0,

(;) (;)()

(;) for 0.

uxt uxt t

uxt t

⎧

⎪

⎨

≥

⎪

⎩

(12.2.26)

112

MECHANICAL SYSTEMS, CLASSICAL MODELS