Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

dynamic equilibrium too, at that moment, under the action of the lost forces of

d’Alembert and of the constraint forces which act upon that part.

Theorem 11.1.27' (theorem of rigidity). Assuming that a given discrete mechanical

system subjected to constraints becomes rigid at a certain moment, the conditions of

dynamic equilibrium of the new mechanical system represent necessary conditions for

the motion of the given mechanical system at that moment.

We notice that, applying the theorem of rigidity to all parts of the discrete

mechanical system

S (to all subsystems S ⊂ S ), we get sufficient conditions to

describe the motion. Indeed, taking, e.g., all the subsystems formed by two particles,

there result the conditions of vanishing torsor (it is sufficient to mention only the

conditions concerning the resultants)

ii j j

ik jk

++ +++ =

∑∑

RR RR0ΦΦ , , 1,2,...,ij n= ,

which, obviously, lead to the conditions (11.1.60).

The relation (11.1.59) may be written also in the form

'()

iiiiii

+=+−=+

∑



FF F rΦΦ, 1,2,...,in= ;

it results that only the components

ii i

m =−



rF of the forces

have a contribution to

the motion of the discrete mechanical system, the components

being lost by

equilibrating the constraint forces (the given denomination is thus justified).

We notice that each of the Theorems 11.1.26 and 11.1.26' can stay at the basis of the

Newtonian mathematical model of mechanics, representing each of them a differential

principle of mechanics.

Formally, the Equations (11.1.60), which represent the necessary and sufficient

conditions of dynamic equilibrium (characterizing entirely the motion of the discrete

mechanical system subjected to constraints) do not differ from the relations (4.1.55),

which represent the necessary and sufficient conditions of static equilibrium of such a

system. Hence, all the considerations made for the problems of statics (including the

Theorems 4.1.6' and 4.1.7'), starting from the relations (4.1.55), can be transposed for

the similar problems with a dynamic character, replacing the given forces

and

ik≠

, , 1,2,...,ik n= , by the lost forces

of d’Alembert; e.g., the condition

(4.1.56) leads to the theorem of torsor, characterized by the formula (11.1.53'''). In fact,

we can use all the results in Chap. 4, Sects. 1.2.1–1.2.3. Thus, we may write a necessary

condition for the motion in the form

{

}

{

}

τ+τ =R0Φ

(11.1.61)

or in the form

()

∑

R0Φ ,

()

iii

×+ =

∑

rR0Φ ,

(11.1.61')

stating

Theorem 11.1.24' (theorem of torsor; second form). The motion of a discrete

mechanical system subjected to constraints takes place so that, at any moment, the sum

of the torsor of the lost forces of d’Alembert with respect to a fixed pole and the torsor

of the constraint external forces with respect to the same pole vanishes.

Let be a discrete mechanical system

S subjected to ideal constraints (for which the

virtual work of the constraint forces (3.2.36) vanishes). We start from the necessary and

sufficient equations of motion (11.1.60), written in the form (by

we mean the

resultant of all constraint forces, without distinction between external and internal ones)

+=R0Φ ,

1,2,...,in=

; (11.1.62)

if we perform a scalar product by the virtual displacements

δr , we sum for all particles

of the mechanical system

S and take into account the relation of definition of ideal

constraints (3.2.36), then we obtain the relation

⋅δ =

∑

rΦ ,

(11.1.63)

which represents a necessary condition to describe the motion. Assuming that the

condition (11.1.63) is fulfilled and that the system is subjected to

p holonomic

constraints of the form (3.2.21'') and to

m non-holonomic constraints of the form

(3.2.15), we can use the method of Lagrange’s multipliers; we may thus write

11 1

ii i

ll kki

il k

fλμ

== =

⎛⎞

++ ⋅δ=

⎜⎟

⎝⎠

∑∑ ∑

rΦ∇ α ,

where

λ ,

1,2,...,lp=

μ ,

1,2,...,km=

are non-determinate scalars (Lagrange’s

multipliers) and where we noticed that in a finite double sum one can invert the order of

summation. By a demonstration analogous to that in Chap. 3, Sect. 2.2.9, we get finally,

ll kki

fλμ

++=

∑∑

0Φ∇ α, 1,2,...in= .

(11.1.64)

We find again the relations (3.2.37) which give the constraint forces, the relations

(11.1.64) being thus equivalent to the relations (11.1.62). We can state (the relation

(11.1.63) becomes a sufficient condition too)

Theorem 11.1.28 (theorem of virtual work; d’Alembert-Lagrange). The motion of a

discrete mechanical system subjected to ideal constraints takes place so that the virtual

work of the lost forces of d’Alembert, which act upon it, vanishes for any system of

virtual displacements of the respective mechanical system.

Taking into account the equivalence between the relation (11.1.63), which represents

the theorem of virtual work, and the relations (11.1.62), which represent the form taken

by Newton’s equations, it results that the theorem of virtual work can be considered as

being a principle (the principle of virtual work or the principle of virtual

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

displacements), because – starting from it – one can solve the fundamental problems of

dynamics.

The equations (11.1.64) are known as Lagrange’s equations of the first kind.

Introducing the virtual velocities (3.2.1'), we may write the condition (11.1.63) in the

form

∗

⋅=

∑

vΦ ,

(11.1.63')

the considered principle being thus called the principle of virtual velocities too.

In case of holonomic (of the form (3.2.16

)) or non-holonomic (of the form (3.2.16))

ideal unilateral constraints, the virtual work of the constraint forces verifies the

inequality (3.2.36'). The principle of virtual work is expressed, in this case, in the form

⋅δ ≤

∑

rΦ

(11.1.63'')

for any system of virtual displacements, representing the necessary and sufficient

condition to describe the motion in case of a discrete mechanical system subjected to

ideal unilateral constraints; in this case too, one can make considerations analogous to

those above.

11.1.2.11 General Considerations

The general (universal) theorems of mechanics are expressed in a torsor form

(containing two vector relations) or in a scalar form. The theorem of torsor (including

the theorem of momentum and the theorem of moment of momentum) is expressed by

vector relations between quantities of kinetic nature and given and constraint external

forces (the internal forces do not intervene – this is a great advantage from the point of

view of practical computation). The theorem of kinetic energy is expressed by a scalar

relation between quantities of kinetic nature and given and constraint, external and

internal forces (in this theorem intervene – in general – all types of forces; in case of

catastatic constraints, the constraint forces do not intervene). These seven scalar

relations allow to obtain, in certain conditions, till ten scalar first integrals (the

conservation theorem of momentum allows to write six first integrals, the conservation

theorem of moment of momentum leads to three first integrals, while the conservation

theorem of mechanical energy represents only one first integral).

We notice, after V. Vâlcovici, that one can group the three general Theorems 11.1.5,

11.1.8 and 11.1.10' in the form

int

() ()

cT c P P

⋅+⋅ + = ⋅+⋅ + +vH K vR Mωω,

(11.1.65)

where

{

}

, vω represents a finite rototranslation

()

,const=

JJJJG

ω , while constc = is

a scalar. One can obtain this result effecting a scalar product of each equation (11.1.8)

by the vector

0 ii

c+×+vrvω

1,2,...,in=

, and summing for all the values of the

index

i. If, in particular, the constant quantities

v , ω and c (equivalent to seven scalar

constants) are so that

int

()0

cP P⋅+× + + =vR Mω (eventually, Pdt or/and

int

dPt are exact differentials), then we have

const

cT⋅+× + =vH Kω ,

obtaining a first integral of the system of equations of motion. If we take

0c = , it

results

()

⋅+⋅ = ⋅+⋅

vH K vR Mωω

(11.1.65')

and we can state

Theorem 11.1.29 (theorem of power of the kinetic torsor; V. Vâlcovici). The derivative

with respect to time of the power of the torsor of momenta of a free discrete mechanical

system, with respect to a fixed pole, by a constant finite rototranslation, is equal to the

power of the torsor of the given external forces which act upon this system, with respect

to the same pole.

These relations represent necessary conditions to describe the motion of a

deformable (in general) discrete mechanical system; indeed, in this case the lost forces

of d’Alembert are modelled by bound vectors. In case of a non-deformable discrete

mechanical system, these forces are modelled by sliding vectors, so that these relations

become also sufficient conditions to describe the motion; in fact (as it will be seen in

next chapter), in this case the theorem of torsor entirely characterizes the motion, the

theorem of kinetic energy being a linear consequence of it. In the case of a non-

deformable discrete mechanical system too, we notice that

int

dd 0

WW==, so

that the theorem of kinetic energy takes the simpler form

dd d

TWW=+ , (11.1.55')

while, in the case of scleronomic constraints, we get

ddTW= . (11.1.55'')

Unlike the universal theorems, the theorem of virtual work expresses always a

necessary and sufficient condition to describe the motion, in the hypothesis of ideal

constraints of the discrete mechanical system. This theorem has the advantage to

contain only the given external and internal forces (the constraint forces do not

intervene in computation); the motion can be thus studied without determining,

previously, the constraint forces.

Besides the momentum

H, which is called also kinetic resultant, one can introduce

also the dynamic resultant

11 1

nn n

iiiii

ii i

== =

∑∑ ∑



AA a r

;

(11.1.66)

we notice the obvious relation



AH.

(11.1.66')

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

Analogously, besides the moment of momentum

K (which is a kinetic moment), with

respect to the pole

O, one can introduce also the dynamic moment, with respect to the

same pole,

11 1

() ()

nn n

iii iii

OOi

ii i

== =

==×=×

∑∑ ∑



D D ra rr;

(11.1.67)

we obtain the obvious relation



(11.1.67')

The relations (11.1.53) and (11.1.53'') may be written, in this case, in the form

()

=+=+

∑

AFRRR

ARR=+, 1, 2, 3j = ,

(11.1.66'')

()

iii

OOO

=×+=+

∑

DrFRMM,

Oj Oj Oj

DMM=+

1, 2, 3j =

(11.1.67'')

stating thus:

Theorem 11.1.30 (theorem of dynamic resultant). The dynamic resultant of a discrete

mechanical system subjected to constraints is equal to the resultant of the given and

constraint external forces which act upon this system.

Theorem 11.1.31 (theorem of dynamic moment). The dynamic moment of a discrete

mechanical system subjected to constraints, with respect to a fixed pole, is equal to the

resultant moment of the given and constraint external forces which act upon this

system, with respect to the same pole.

The torsor of momenta

{

}

τ H is called also kinetic torsor; analogously, one can

introduce the dynamic torsor

{

}

τ A . Observing that

{

}

{

}

τ=τ



AH,

(11.1.68)

it results

{

}

{

}

{

}

ii i

OOO

τ=τ+τAFR

(11.1.68')

and we can state

Theorem 11.1.32 (theorem of dynamic torsor; Newton-Euler). The dynamic torsor of a

discrete mechanical system subjected to constraints, with respect to a fixed pole, is

equal to the torsor of the given and constraint external forces which act upon this

system, with respect to the same pole.

Taking into account (11.1.65), we may write

int

()

cT c P P⋅+⋅ + = ⋅+⋅ + +



vA D vR M

ωω

(11.1.65'')

too; in the particular case

0c = , we state

Theorem 11.1.29' (theorem of power of the dynamic torsor). The power of the dynamic

torsor of a free discrete mechanical system, with respect to a fixed pole, by a constant

finite rototranslation, is equal to the power of the torsor of the given external forces

which act upon this system, with respect to the same pole.

Obviously, the influence of the constraint forces may be also introduced in the

Theorems 11.1.29 and 11.1.29'.

These results are equivalent to those previously obtained; besides, they can give

sometimes useful information concerning the motion of a discrete mechanical system

From the above exposition (as a completion to Chap. 1, Sect. 1.2.3), one can affirm

that, by conjugating elements of kinematics with elements of mass geometry, one

obtains the kinetics, which deals with the motion of mechanical systems supplied with

mass, without taking into account the forces which act upon them; if the forces

intervene too, then one has to do with dynamics.

11.1.2.12 Group Properties

Let be the system of equations of motion (11.1.8). Let us also assume that the given

forces are conservative (or quasi-conservative) in their totality, deriving from the simple

potential (or quasi-potential)

===

∑∑∑

rr r rr r rr rrrr

12 12

111

( , ,..., , , ,..., ; ) ( , ; ) ' ( , , , ; )

nnn

iii i i

ik k k

iik

UtUtUt

   

(11.1.69)

in the form

∑

FF∇ ,

iii

U=F ∇ ,

()

ik ik ki

UU=+F ∇ , , 1,2,...,ik n= ;

(11.1.69')

for the sake of generality we assume that the potential (quasi-potential) depends on

velocities too.

In case of a transformation of the form

0ii

′

rrr,

const=

JJJJG

r ,

′



rr,

1,2,...,in=

, tt

′

= ,

(11.1.70)

which belongs to the group of space translations

T, with three parameters (see Chap. 6,

Sect. 1.2.3 too), we may write

12 12 0

( , ,..., ) ( , ,..., )

UU U

′′ ′

−=⋅

∑

rr r rr r r ∇

corresponding to Lagrange’s theorem. Hence, if

12 12 12 12

( , ,..., , , ,..., ; ) ( , ,..., , , ,..., ; )

nn nn

UtUt

′′ ′ ′′ ′

   

rr rrr r rr rrr r ,

(11.1.71)

then we have

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

∑

0∇

(11.1.71')

too, the sum of the given forces vanishing. We can thus state

Theorem 11.1.33 If the simple potential (quasi-potential) of the given conservative

(quasi-conservative) forces which act upon a free discrete mechanical system is

invariant with respect to the group of space translations

T, then the momentum of this

system is conserved in time.

Taking into account the relation

′′

−=−

rr rr, we notice that the relation

(11.1.71) takes place if

(;)

iii

UU t=



r , (,,;)

ik ik k k

UU t=−



rrrr , , 1,2,...,ik n= ,

hence if the external forces vanish (isolated mechanical system), while the internal

forces depend on the distances between two particles (

()

;

ik ik k

PP t=

JJJG

FF , verifying

the principle of action and reaction).

As well, in case of a transformation of the form (

α is a constant tensor of second

order)

′

rrα ,

′



rrα ,

1,2,...,in=

, tt

′

= ,

(11.1.70')

which belongs to the group SO(3) of finite rotations with three parameters (special

orthogonal group in

E ), we notice that the relations

()( )

() () ()()

()()

ik ik

mp m mp

ii j jm

k k jl jl

xx xxαα ααδ

′′

⋅= ⋅ = ⋅ =

rr r r i iαα

()() ()() ()()ik ik ik

jp i

llp k

llll

xx xx xxαα δ====⋅rr,

′′

⋅=⋅

 

rr rr

and, in particular, the relations

′



, 1,2,...,ik n=

, take place; one

can also show that these relations occur only in case of a transformation of the form

(11.1.70'). In such conditions, a theorem of Cauchy allows to state that a relation of the

form (11.1.71) takes place only and only if (the dependence on velocities has not been

mentioned)

()

222

11 21 3 1 2 122 3 1

, , ,..., , , , ,..., ,

nnn

−

=⋅⋅⋅⋅⋅ ⋅rr rr r r rr rrr r r rr .

We can write

()

() () ( )

1 1 11

n n nn

i im

jkl l jkl l

j j

i im

i i im

U U

U x x x

x xx

= = ==

∂ ∂

×=∈ =∈ =

∂ ∂

∑ ∑ ∑∑

r i i0∇

as a product of two tensors, one symmetric and the other skew-symmetric with respect

to the indices

j and k, the resultant moment of the given forces being thus equal to zero.

We state

Theorem 11.1.34 If the simple potential (quasi-potential) of the given conservative

(quasi-conservative) forces which act upon a free mechanical system is invariant with

respect to the group SO(3) of finite rotations, then the moment of momentum of this

system is conserved in time.

Noting that

′′

−=−rr rr

′′

−=−

 

rr rr

′

rr,

′



rr,

we can state that the relation (11.1.71) takes place if (we have

()

;

ik ik k

PP t=

JJJG

FF ,

verifying the principle of action and reaction)

()

iiii

UU t=



rr ,

()

ik ik k k

UU t=−−



rrrr , , 1,2,...,ik n= .

By a transformation of the form

′

rr,

′



rr, 1,2,...,in= ,

ttt

′

=+,

constt = ,

(11.1.70'')

of the temporal variable, which belongs to the Abelian group of time translations

with one parameter, we can write

() () /Ut Ut t U t tU

′

−=∂∂=



, using Lagrange’s

theorem. If

() ()Ut Ut

′

= , then it results () 0Ut =



too, so that one cannot have a

quasi-potential (hence, nor a quasi-conservative force). If

(,,..., )

UU= rr r , non-

depending on velocities, hence if

()

iii

UU= r , (, )

ik ik k

UU= rr , , 1,2,...,ik n= (in

fact,

()

ik ik k

UU=−rr, to can verify the basic principle of the internal forces), then

=⋅

∑

r∇

and we may state

Theorem 11.1.35 If the simple potential of the given conservative forces which act

upon a free mechanical system is invariant with respect to the group of time

translations

T, then the mechanical energy of this system is conserved in time.

Finally, let be a transformation of the form

0ii

′

=+rrv,

0ii

′



rrv,

const=

JJJJG

, 1,2,...,in= , tt

′

= ,

(11.1.70''')

which belongs to the Abelian group

Γ of Galileo, with three parameters. We notice that

the acceleration



, hence the dynamic resultant A, given by (11.1.66), is invariant to

such a transformation too. In the conditions of the Theorem 11.1.33, it results

=A0,

while the potential (quasi-potential)

U is invariant to a transformation of the form

(11.1.70); a relation of the form (11.1.71) takes place also with respect to the

transformation (11.1.70''') if

()

UUt= ,

()

ik ik k k

UU t=−−



rrrr , as a

particular case (the mechanical system is isolated, while the internal forces verify the

principle of action and reaction). Taking into account the theorem of motion of the mass

centre, we may state

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

Theorem 11.1.36 If the simple potential (quasi-potential) of the given conservative

(quasi-conservative) forces which act upon a free discrete mechanical system is

invariant with respect to the Galileo group, then the mass centre of this system has a

uniform rectilinear motion with respect to an inertial frame of reference.

The four groups of transformations considered are subgroups of the Galileo-Newton

group

G, with ten parameters, leading to the three vector and one scalar first integrals

(hence, to the ten scalar first integrals) mentioned above.

We will use the group properties to determine the first integrals of the equations of

motion in a unitary theory, in the frame of Lagrangian and Hamiltonian mechanics.

11.2 Dynamics of Discrete Mechanical Systems with Respect

In what follows, we present the form taken by the general theorems of mechanics with

respect to a non-inertial frame of reference; to this goal, we compute first of all the

mechanical quantities previously introduced (momentum, moment of momentum,

kinetic energy, work, power) with respect to such a frame. Especially, if the frame has

the pole at the mass centre of the considered discrete mechanical system, then the

results obtained have a remarkable form.

11.2.1 Motion of a Discrete Mechanical System with Respect

We introduce a Koenig frame of reference with respect to the mass centre of a discrete

mechanical system and present the general and conservation theorems with respect to

such a frame. We make also some considerations concerning the problem of

n bodies.

11.2.1.1 Koenig’s Frame of Reference. Koenig’s Theorems

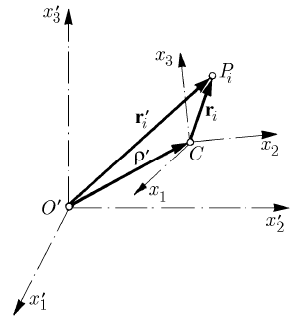
By a Koenig frame of reference we mean a non-inertial frame

R, of axes

1, 2, 3i = (movable with respect to the inertial frame

′

R , of axes

′′

, 1, 2, 3j = ,

considered fixed), which has its pole at the centre of mass

C (of position vector

′

) of

the discrete mechanical system

S and which does not rotate (it moves with the axes

parallel to themselves) with respect to the frame

′

R (Fig. 11.6). One passes from the

frame

′

R to the frame R by relations of the form

′′

() ()ii

xxρ

′

, 1,2,...,in= , 1, 2, 3j = ;

(11.2.1)

because

0ω= , in conformity to the hypothesis made above, it results that

′′



, 1,2,...,in= .

(11.2.1')

In this case, the momentum is given by (we denote by “prime” the quantities

calculated with respect to the fixed frame

′

R )

to a Non-inertial Frame of Reference

to a Koenig Frame of Reference

()

ii i i

mm M

′′ ′′

== +=

∑∑



Hr r

ρρ

(11.2.2)

where we took into account the relations (properties of the mass centre)

∑

r0,

∑



r0;

(11.2.1'')

this result is known and may be obtained by differentiating the relation (3.1.9) with

respect to time.

The moment of momentum is expressed in the form

()()

()

iii ii i

′

′′′ ′ ′

=× = +×+

∑∑



Krr r r

ρρ

11 11

()

nn nn

iii ii ii i

ii ii

mm m m

== ==

⎛⎞

′′ ′′

=× + ×+× +×

⎜⎟

⎝⎠

∑

∑∑∑



rr r rρρ ρρ ,

Fig. 11.6 Motion with respect to a Koenig frame of reference

wherefrom one gets the relation

()

′

′′′

=+×



ρρ

(11.2.3)

()C

being the moment of momentum of the system with respect to the centre of mass

(in the relative motion, with respect to a Koenig frame with the pole at

C ); we can thus

state

Theorem 11.2.1 (S. Koenig). The moment of momentum of a discrete mechanical

system with respect to a fixed pole is equal to the sum of the moment of momentum of

the same system with respect to the pole of a Koenig frame of reference and the moment

of momentum of its mass centre at which the whole mass of the mechanical system is

concentrated, with respect to the fixed pole.

11 Dynamics of Discrete Mechanical Systems