Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

11.1.2.6 Conservation Theorems of Moment of Momentum. Theorem of Areas.

Applications

If the moment

M of the given external forces is contained in a fixed plane (is normal

to a fixed axis

Δ, O Δ∈ , of unit vector u, with respect to the frame of reference R or

has a zero component,

⋅=Mu ), as in the case of a single particle (see Chap. 6,

Sect. 1.2.5), then the theorem of moment of momentum leads to

() ()

(, ,)

iii j i

OOjjkll

mKu mxvuC

⋅= = =∈ =

∑∑

Ku r vu , constC = ,

(11.1.31)

obtaining thus a scalar first integral of the equations of motion; in this case, the

projection of the moment of momentum

K on the axis Δ is conserved in time. If, in

particular, the axis

Δ coincides with the Ox-axis, then

()( )

() () () () () () () ()

12 21 12 21

ii ii ii ii

mxv xv mxx xx C

−= −=

∑∑



constC =

(11.1.31')

As well, if the moment

M has a fixed support (is normal to two non-parallel fixed

axes

Δ and

Δ with respect to the frame R or has two zero components), then we

get two independent scalar first integrals of the form (11.1.31), while the projection of

the moment of momentum of the discrete mechanical system

S on a plane normal to

the moment

M (determined by the two fixed directions) is conserved in time.

=M0 (the moment

M is normal to three distinct directions), then we can set

up three independent scalar first integrals of the form (11.1.31). Besides, the relation

=M0 leads to



K0 and to

()

iii

=× =

∑

KrvC, const=

JJJJG

C ,

() ()

Oj jkl

KmxvC

= ∈ =

∑

, 1, 2, 3j = ,

(11.1.31'')

hence to a vector first integral, equivalent to three scalar first integrals; we may thus

state

Theorem 11.1.15 (conservation theorem of moment of momentum). The moment of

momentum of a free discrete mechanical system, with respect to a fixed pole, is

conserved in time if and only if the resultant moment of the given external forces which

act upon this system, with respect to the same pole, vanishes.

The two conservation theorems (of momentum and of moment of momentum) are

independent each other and give nine independent scalar first integrals. They can be

grouped together in the form (we assume that

{

}

τ=F0)

{}

const

τ=

JJJJG

(11.1.31''')

and we can state (if the torsor of a system of bound vectors vanishes with respect to a

pole, then it vanishes with respect to any other pole)

Theorem 11.1.16 (conservation theorem of torsor). The torsor of the momenta of a free

discrete mechanical system, with respect to a fixed pole, is conserved in time if and only

if the torsor of the given external forces which act upon this system, with respect to the

same pole, vanishes.

Projecting the particles

P , 1,2,...,in= , of the free discrete mechanical system S

on a fixed plane (e.g., the plane

Ox x ) and supplying the projections

′

with the

same masses

m (or assuming that we have to do with a plane mechanical system), we

can write, in polar co-ordinates (

()

cos

xrθ= ,

()

sin

xrθ= ),

()

() () () () ()

12 21

111

nnn

ii ii i

iiiii

iii

K mxx xx mr mθΩ

===

=−==

∑∑∑





We thus find again the second formula (11.1.3) for

3j = . If

M = , then the

formula (11.1.31') leads to

()

iiii

mmrCΩθ

∑∑



, constC = ,

(11.1.32)

and we may state

Theorem 11.1.17 (theorem of areal velocities; plane case). The sum of the products of

the double masses of the particles of a free discrete mechanical system by the areal

velocities of their projections on a fixed plane, with respect to a fixed pole in this plane,

is conserved in time if and only if the resultant moment of the given external forces

which act upon this system, with respect to an axis normal to the considered plane at

the same pole, vanishes.

This theorem can be applied, e.g., if the supports of all the given external forces

pierce a fixed straight line. Observing that

() ()

3 3

d/d

i i

O O

tΩ = A

, where we supplied the

area by the sign +, corresponding to a positive rotation in the considered fixed plane

(see also Fig. 6.5), we get (integrating from the initial moment

t )

()

2()

mCtt

=−

∑

A , constC = ,

(11.1.32')

and are led to

Theorem 11.1.18 (theorem of areas; plane case; L. Euler, D. Bernoulli, d’Arcy). The

sum of the products of the double masses of the particles of a free discrete mechanical

system by the areas described by the radii vectores of their projections on a fixed plane,

with respect to a fixed pole in this plane, starting from their initial positions, is in direct

proportion to the interval of time travelled through if and only if the resultant moment

of the given external forces which act upon this system, with respect to an axis normal

to the considered plane at the same pole, vanishes.

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

We notice that the Theorems 11.1.17 and 11.1.18 are equivalent.

If the angular velocity is the same for all particles (

θω=



, 1,2,...,in= ), then the

relation (11.1.32) reads

ICω = , (11.1.32'')

where

II= is the moment of inertia of the mechanical system S with respect to

the

Ox -axis, defined by the relation (3.1.21'). This relation takes place, e.g., in case of

a non-deformable mechanical system

S in motion of rotation with respect to a fixed

axis. The constant

C is called the constant of areas.

In particular, if at a moment

tt=

the discrete mechanical system S is at rest with

respect to a fixed (inertial) frame of reference

R (

() 0

tθ =



and

()

() 0

tΩ = ),

hence if the mechanical system

S begins to move starting from a position of rest, then

the constant of areas vanishes (

0C = ); thus, it results

()

iiii

mmrΩθ

∑∑



()

∑

0I ω =

(11.1.32''')

Hence, if some particles have an angular velocity in one sense (e.g.,

θ >



), then for

the other particles the velocity must be of opposite sense (

θ <



); one can make this

observation for the areas

()

too. From the third relation (11.1.32''') one can see that

0ω = ; hence, the mechanical system S cannot rotate around the fixed axis if it is at

rest with respect to the latter one at the initial moment. For instance, a man (in general,

a living being) in a vertical position on a perfect smooth ground cannot rotate about a

vertical axis passing through its centre of mass (he is acted upon only by his own

weight and by the normal constraint force of the ground, the resultant moment of the

external forces with respect to the centre of mass vanishing). The rotation takes place

only if a pivoting friction between man and ground intervene too (as in case of walking)

or by various complicated motions made by the man, as we will see later.

The above results have many applications. Thus, we will consider a non-deformable

mechanical system

S, which has a moment of inertia I

with respect to a fixed axis in

the inertial frame of reference

R and rotates with an angular velocity

ω about this

axis, and a particle

P (or another non-deformable mechanical system

), which has a

moment of inertia

I with respect to the same fixed axis and which rotates with an

angular velocity

ω with respect to the system S, hence with an angular velocity

′

ωω ω with respect to the frame R ; we assume that the resultant moment of

the external forces which act upon the mechanical system

{}

P= ∪

′

SS (or

= ∪

′

SSS) vanishes. The conservation theorem of moment of momentum allows

to write

()

IIIII

′

+++C

SS S S

ωω= ωω=, const=

JJJJG

C ;

(11.1.33)

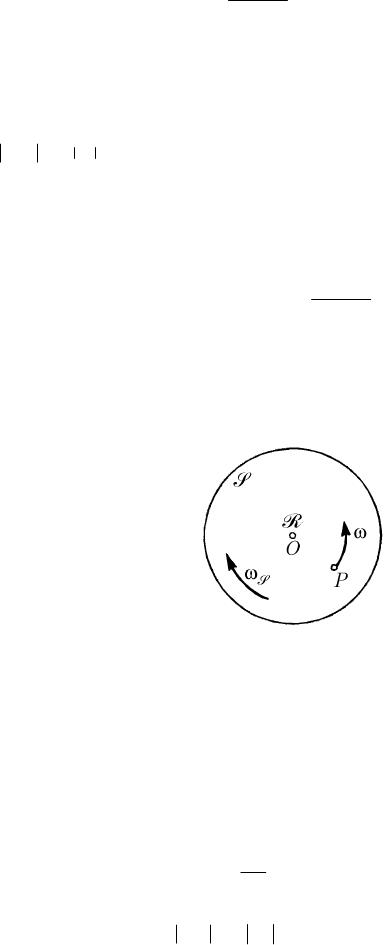
if the mechanical system

′

S is at rest with respect to the frame R at the initial

moment

t (

() ()tt

′

==0

ωω , hence

()t = 0ω ), then we get =C0, so that

II+

ω=− ω.

(11.1.33')

Hence, if the particle

P begins to rotate with the angular velocity ω with respect to the

non-deformable system

S, the latter one also moves with an angular velocity

ω of

opposite sense (Fig. 11.3); supposing that

II

(hence

()

//II I II+≅

), it

results



ωω. We may assume that the rotations take place about the same

-Ox axis, which passes through the pole O, the angular velocities being specified by

the scalar magnitudes

()tω

and ()tω , respectively (hence, () () ()tttωω ω

′

too); it results

0IIωω

′

ωω

=− .

(11.1.34)

Integrating with respect to time, we obtain

constIIIIθθ θθ

′′

++=

SS SS

= ,

(11.1.34')

Fig. 11.3 Motion of rotation of a mechanical system

where

()tθθ=

()tθθ

′′

. Denoting by

ϑθ θ=−

ϑθθ

′′′

=−

the

rotation of the mechanical system

S and the rotation of the particle P, respectively,

considered to be positive for the positive sense of rotation, we get the angle of rotation

of the mechanical system

S as a function of the angle of rotation of the particle P (of

an opposite sense with respect to the latter one)

ϑϑ

′

=−

;

(11.1.34'')

II

, then it results ϑϑ

′



too. These results are analogous to those

obtained at the precedent subsection for a motion of translation, in case of a similar

problem.

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

Returning to the rotation of a man about a vertical axis on a perfect smooth ground,

case considered above, we notice that to any tendency of rotation of the upper part of

his body (determined by internal forces) corresponds a tendency of rotation of the lower

part of his body in the opposite sense. If the man would hold up his hands, with the fists

in symmetrical positions with respect to the axis, and would effect by each fist a motion

of rotation in the same sense, in a horizontal plane, the symmetry with respect to the

axis being preserved, then his body would rotate in an opposite sense. As well, as it was

shown by Saint-Germain, if the man would rotate several loads hanged simultaneously

on a belly-band (by the action of internal forces) in the same sense, then his body would

rotate in an opposite sense. Let us consider also the case of a circular disc, in a

horizontal plane, which can rotate without friction about a vertical axle which passes

through its centre (Prandtl’s disc); we have seen that a particle which describes a circle

with the centre on the vertical axis induces a rotation of the disc in the opposite sense

(Fig. 11.3). If a man is in a vertical position on the disc, his centre of mass being on its

axis, and keeps in his hands a wheel, the axle of which is along the same vertical axis,

then any rotation of the wheel (provoked by an external cause) leads to a rotation of the

system (formed by the man and the disc) in an opposite sense.

If the constant of areas is non-zero (

≠C0), corresponding to the formula (11.1.33),

then one can obtain an angular velocity non-parallel to

C only if the angular velocity ω

has a direction different from that of

C; returning to Prandtl’s disc, the axle of the wheel

must be inclined with respect to the vertical. As well, the formula (11.1.32'') shows that

the angular velocity

ω is in inverse proportion to the axial moment of inertia

I ; for

instance, a ballerina (or a skater) rotates with a greater angular velocity if she (he) has

the hands pressed to the body (the axial moment of inertia is smaller) or with a smaller

angular velocity if she (he) stretches the hands from the body (the axial moment of

inertia is greater).

Analogously, a cosmic vehicle may change its direction of motion only if it is in a

gravitational field. The manoeuvres effected in the vehicle are, in fact, actions of

internal forces; an intervention of external forces, to give the vehicle the possibility of

rotation, is necessary.

If the Theorem 11.1.15 takes place, then we can write conservation relations of the

form (11.1.32) for the three planes of co-ordinates; we obtain thus

()

∑

CΩ

, const=

JJJJG

C ,

(11.1.35)

and may state

Theorem 11.1.17' (theorem of areal velocities; space case). The sum of the products of

the double masses of the particles of a free discrete mechanical system by their areal

velocities, with respect to a fixed pole, is conserved in time if and only if the resultant

moment of the given external forces which act upon this system, with respect to the

same pole, vanishes.

In this case, the constant moment of momentum

K is equal to the constant of areas

C (

=KC

). We can write a theorem of areal velocities in the plane case for any

plane passing through

O and of normal of unit vector k, the corresponding constant of

areas being

C =⋅Ck. In case of a plane Π normal to

K , the constant of areas will

take its maximal value (equal in modulus to

); the respective plane is called the

plane of the maximum of areas. If

⊥kC, hence if the moment of momentum

K is

contained in the plane

Π, then the constant of areas vanishes. By integration in the

plane

Π, starting from the initial moment

, we can write

()

2()

mCtt

=−

∑

A ,

(11.1.35')

where

C is the corresponding scalar constant of areas; we can state

Theorem 11.1.18' (theorem of areas; space case). The sum of the products of the

double masses of the particles of a free discrete mechanical system by the areas

described by the radii vectores of their projections on any fixed plane passing through

a fixed pole, with respect to that pole, starting from their initial positions is in direct

proportion to the interval of time travelled through if and only if the resultant moment

of the given external forces which act upon this system, with respect to the same pole,

vanishes.

11.1.2.7 Conservation Theorems of Mechanical Energy. Applications

In the theorem of kinetic energy, expressed by the formula (11.1.24),

dT is a

differential, but

dW and

int

dW are not, in general, exact differentials; if the sum of the

elementary works is an exact differential

int

dd dWW Φ+=, (,;)

tΦΦ=



rr ,

(11.1.36)

then, by integration, we can obtain a first integral of energy in the form

ThΦ=+, consth = . (11.1.36')

A first important case to be considered is that in which the given internal forces are

conservative ones, deriving from a simple potential (

int

ddWU= ) or from a

generalized potential (

int

ddWU= ); we say also that the mechanical system S is, in

this case, a natural mechanical system. Going from the expression (3.2.4) of the internal

elementary work, we notice that, in the particular case in which the internal forces are

of the form

()

ik ik ik

FFr= , we obtain a simple potential (the prime to the sign

∑ indicates a summation for ki≠ )

'd const

ik ik

UFr

∑∑

∫

(11.1.37)

where

r is the distance between two particles

P and

P of the discrete mechanical

system

S. For instance, in case of internal forces of attraction, in direct proportion to

the distance, we read

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

ik ki ik ik ik k

kk=− = = −FF r rr,

ik ik ik

Fkr=− ,

ik ik

Ukr

=− >

∑∑

, 0

k > ,

, 1,2,...,ik n=

(11.1.37')

Passing to the space

E of co-ordinates

X , specified by the relation (11.1.10), we

may write

int

11 1

d'dd

nn n

ik k k

ik k

WQX

== =

=⋅=

∑∑ ∑

Fr ,

()

kkll

QQXX=



(11.1.38)

so that, in case of a simple potential

U, it results

∂

()

UUX= , 1,2,...,3kn= ,

(11.1.38')

while, in case of a generalized potential, we get

[]

∂∂

⎛⎞

==−

⎜⎟

∂

⎝⎠



()

UUXX=



, 1,2,..., 3kn= .

(11.1.38'')

As we have seen in Chap. 1, Sect. 1.1.12 and in Chap. 6, Sect. 1.1.2, the generalized

potential can be only of the form

UUXU

∑



()

kkl

UUX= ,

()

UUX= ,

(11.1.39)

so that it results

kl k

XX X

∂∂

∂

⎛⎞

=−+

⎜⎟

∂∂ ∂

⎝⎠

∑



(11.1.39')

and then

int

ddd

WQXU

∑

(11.1.39'')

Hence, in case of conservative internal forces we may write the relation

dddTUW=+

(11.1.40)

or the relation

dd dTU W=+

; (11.1.40')

introducing the potential energy

VU=− , in case of a simple potential, or the potential

energy

VU=− , in case of a generalized potential, we can write

intPP

WVVV=−=−Δ

intPP

VW V=− +

. (11.1.41)

It results that the potential energy of a free discrete mechanical system acted upon by

conservative internal forces (natural mechanical system) is equal to the internal work

with changed sign, effected by the internal forces, starting from the initial moment

(excepting an arbitrary constant

V , which represents the potential energy at the initial

moment; frequently, one chooses

V so as a minimum of the potential energy be equal

to zero).

Denoting the mechanical energy by

ETV=+, we get

dd( )dETVW=+=,

(11.1.42)

stating thus

Theorem 11.1.19 (theorem of mechanical energy; Helmholtz). The differential of the

mechanical energy of a free discrete mechanical system, acted upon by conservative

internal forces (natural mechanical system), is equal to the elementary work of the

given external forces which act upon this system.

Dividing the relation (11.1.42) by

dt and taking into account (11.1.7), we have



(11.1.42')

and may state

Theorem 11.1.19' (theorem of mechanical energy; second form). The derivative with

respect to time of the mechanical energy of a free discrete mechanical system, acted

upon by conservative internal forces (natural mechanical system), is equal to the power

of the given external forces which act upon this system.

In general, the elementary work of the given external forces is not an exact

differential, so that we can write

2121

() () d d

EEt Et E E W t Pt

Δ= − = − = = ⋅ =

∑

∫∫

Fv ,

(11.1.42'')

stating thus

Theorem 11.1.19'' (theorem of mechanical energy; finite form). The variation of the

mechanical energy of a free discrete mechanical system, acted upon by conservative

internal forces (natural mechanical system), in a finite interval of time, is equal to the

work effected by the given external forces which act upon this system in the considered

interval of time.

Applying the principle of action and reaction to the external forces

F correspond

the forces

=−fF, which represent the actions of the considered discrete mechanical

system upon some external mechanical systems. The relation (11.1.42'') allows to write

EE t

−= ⋅

∑

∫

fv ,

(11.1.42''')

11 Dynamics of Discrete Mechanical Systems

MECHANICAL SYSTEMS, CLASSICAL MODELS

so that we can state

Theorem 11.1.19''' (theorem of mechanical energy; second finite form). The lost

mechanical energy of a free discrete mechanical system, acted upon by conservative

internal forces (natural mechanical system), in a finite interval of time, is equal to the

work effected by this system on the external mechanical systems, in the same interval of

time.

We can say that this represents an exit for the considered mechanical system.

We may write the relation (11.1.42'') also in the form

EW E=+

; (11.1.42

)

hence, the mechanical energy of a free discrete mechanical system, acted upon by

conservative internal forces (natural mechanical system), is equal to the external work

effected by the given external forces, starting with the initial moment (excepting an

arbitrary constant

E , which represents the mechanical energy at the initial moment, as

in the case of the potential energy; as well, we can choose

E so that a minimum of the

potential energy be equal to zero).

d0W = for a certain interval of time, then the relation (11.1.42) leads to

ETV h=+=

consthT V=+=

, (11.1.43)

and we can state

Theorem 11.1.20 (conservation theorem of mechanical energy). The mechanical

energy of a free discrete mechanical system, acted upon by conservative internal forces

(natural mechanical system), is conserved in a certain interval of time if and only if the

elementary work of the given external forces which act upon this system vanishes in the

same interval of time.

In particular, this theorem can be applied to a closed (isolated) mechanical system,

for which intervene only internal forces. By applying the conservation theorem of

mechanical energy, a part of the kinetic energy is transformed in potential energy, if

decreases, or a part of the potential energy is transformed in kinetic energy, if

increases; hence, the mechanical energy is conserved as a whole, but it is in continuous

transformation. For instance, for a heavy particle

P of mass m, which falls on the Earth

surface from the height

h, without initial velocity, along the Ox-axis (situated along the

ascendent vertical), we can write

mv mgx mgh+=

;

(11.1.44)

x varies from h to 0, then v increases from 0 to

max

v (the kinetic energy increases

from

0 to

max

Tmgh= ), while the potential energy decreases from

max

Vmgh= to 0

(excepting an arbitrary constant). The influence of the motion of the Earth has been

neglected in this formula. The above results remain valid also for the continuous

mechanical systems, as we will see in the next chapter.

Let thus be an elastic blade

AB, built-in at A, at rest (of zero potential and zero

kinetic energy, hence zero mechanical energy too) in a vertical position (Fig. 11.4); we

neglect the weight of the blade, the resistance of the air as well as other external forces,

and we assume that the internal forces are conservative. We apply an external force at

the free end

B, which becomes a new position B

′

; one obtains thus a mechanical

energy equal to the external work

W (one uses the theorem of mechanical energy). At

this position, the kinetic energy vanishes, while the potential energy is equal to

W. If

the action of the external force ceases, then the elastic blade tends to come back at the

stable position of equilibrium

AB; the potential energy decreases till it vanishes, while

the kinetic energy increases till its maximal value at the position

AB (the conservation

theorem of mechanical energy is applied). Due to the velocities of various points of the

blade, that one passes beyond the position of equilibrium, in a new position

′′

symmetric to the position

′

with respect to AB; the potential energy has of new a

maximal value, while the kinetic energy vanishes. Thus, by transformations of energy,

the blade oscillates about the stable position of equilibrium

AB.

Fig. 11.4 Application of the conservation theorem of mechanical energy

If, in general, we assume that the external forces are also conservative (deriving from

a simple or a generalized potential), we can write

ext

ddWU= ; (11.1.45)

introducing an external potential energy

ext

VU=− (unlike V, which is called internal

potential energy too), the relation (11.1.42) leads to a conservation theorem of energy

of the form

TVV h++=, consth = .

(11.1.46)

If we transmit to a mechanical system a certain mechanical energy (as in the case of

the elastic blade) and then we leave it free, the motion continues without loss of

mechanical energy; only transformations of kinetic energy in potential energy and vice

versa take place. We obtain thus a mechanical perpetuum mobile. But the experiment

shows that one cannot realize apparatuses corresponding to such a phenomenon (e.g.,

the elastic blade considered above cannot reach practically a position

′′

, symmetric

11 Dynamics of Discrete Mechanical Systems