Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

478 16. Nonlinear Hyperbolic Equations

In fact, assuming genuine nonlinearity, we can arrange that '

I/ be a C

curve, after perhaps a further reparameterization of '

I/. To see this, we com-

pute the second -derivatives at  D 0. This time, for notational simplicity, we

denote the j -shock curve by '

./ and the j -rarefaction curve by '

./.

Recall that, given (7.22), the second equation in (7.20) becomes

(7.42) '

./ D r



./



Differentiation of this plus use of (7.26) yields

(7.43) '

.0/ Dr

Next, we take the -derivative of (7.33). Set A./ D A



./



.Weget

(7.44)



A./  s

./



./ C



./  s

./



./

D s

./



./  u



C s

./'

./:

Thus, since s

.0/ D 

/ and '

.0/ D r

/,wehave

(7.45)



A.0/  



.0/ D



.0/  A

.0/



Now A./r



./



D 



./





./



. Let us write this identity as



A./ 



./



./ D 0 and differentiate, to obtain

(7.46)



A.0/  



.0/ D





.0/  A

.0/



Subtracting from (7.45), we get

(7.47)



A.u

/  





.0/  r

.0/





.0/  

.0/



Now the left side of (7.47) belongs to V

, which is complementary to the span of

/, so both sides of (7.47) must vanish. This implies

(7.48) s

.0/ D



.0/ D

.0/ r

/ D

;

and, since '

.0/  r

.0/ belongs to the null space of A.u

/  

(7.49) '

.0/ D r

.0/ C ˇr

for some ˇ 2 R.

7. Systems of conservation laws in one space variable; Riemann problems 479

Note that r

.0/ coincides with the quantity in (7.43). We claim that we can

reparameterize '

./ so that ˇ D 0 in (7.49), by taking

(7.50) e'

./ D '. C ˛

for appropriate ˛. Indeed, we have e'

.0/ D '

.0/; e'

.0/ D '

.0/,and

(7.51) e'

.0/ D '

.0/ C 2˛'

.0/ D '

.0/ C 2˛r

Thus, taking ˛ Dˇ=2 in (7.50) accomplishes this goal. Replacing '

./ by

(7.50), we arrange that the curve '

I/ is C

in .

Note that if u

D '

I/,forsome 2 .

;0, the identity (7.48) together

with (7.35) implies that the shock speed s D s

./ of the weak solution (7.17)

satisﬁes 

/<s<

/, at least if  is close enough to 0.Inviewofthe

ordering of the eigenvalues of A.u/, we have the inequalities

(7.52)



j 1

/<s<



/<s<

j C1

for  sufﬁciently close to 0. These are called the Lax j -shock conditions.The

corresponding weak solutions are called shock waves.

The function '

I/ is in fact C

in .u

I/. We can deﬁne a C

-map

(7.53) ‰.u

I

;:::;

/ D '



L1



.'

/I

/ /I

L1



I



Since .d=d /'

I0/ D r

/ and the eigenvectors r

/ form a basis of R

we can use the inverse function theorem to conclude the following:

Proposition 7.1. Assume the L  L system (7.1) is strictly hyperbolic and gen-

uinely nonlinear in each ﬁeld. Given u

2 , there is a neighborhood O of u

such that if u

2 O, then there is a weak solution to (7.1) with initial data

(7.54)

u.0; x/ D u

; for x<0;

; for x>0;

consisting of a set of rarefaction waves and/or shock waves satisfying the Lax

conditions (7.52).

See Fig. 7.2 for an illustration, with L D 4.

We consider how Proposition 7.1 applies to some examples. First consider the

system (7.14), arising from the second-order equation (7.11). Here, with r

and



given by (7.16), we have

(7.55) r

r

D˙

1=2

480 16. Nonlinear Hyperbolic Equations

FIGURE 7.2 Shocks and Rarefactions

The strict hyperbolicity assumption is K

¤ 0 on . Given this, the hypothesis

of genuine nonlinearity is that K

is nowhere vanishing. To achieve (7.22), we

would rescale r

, changing it to

(7.56) r

D2



1



In this case, given u

D .v

/ 2   R

, the rarefaction curves emanating

from u

are the forward orbits of the vector ﬁelds r

and r



, starting at u

.The

jump condition (7.29) takes the form

(7.57)

 w

D s.v

 v

K.v

/  K.v

/ D s.w

 w

in this case. This requires K.v

/  K.v

/ D s

 v

/,so

(7.58)

 w

 v

D˙

K.v

/  K.v

 v

This deﬁnes a pair of curves through u

; half of each such curve makes up a shock

curve.

One occurrence of (7.11) is to describe longitudinal waves in a string, with

V.t;x/ denoting the position of a point of the string, constrained to move along

the x-axis. Physically, a real string would greatly resist being compressed to a

degree that V

D v ! 0. Thus a reasonable potential energy function F.v/ has

the property that F.v/ !C1as v & 0; recall K.v/ D F

.v/. A situation

yielding a strictly hyperbolic, genuinely nonlinear PDE is depicted in Fig. 7.3,in

which F is convex, K is monotone increasing and concave, K

is positive and

monotone decreasing, and K

is negative. Here,  Df.v; w/ W v>0g.

We illustrate the rarefaction and shock curves through a point u

2 ,in

Fig. 7.4, for such a case.

A speciﬁc example is

(7.59) F.v/ D

1 C v

;K.v/D 1 

.v/ D

.v/ D

7. Systems of conservation laws in one space variable; Riemann problems 481

FIGURE 7.3 Typical String Potential

FIGURE 7.4 Rarefaction and Shock Curves Through u

482 16. Nonlinear Hyperbolic Equations

FIGURE 7.5 Solutions to Riemann Problems

In Fig. 7.5 we illustrate the solution of the Riemann problem (7.17), with u

D u

and u

D u

, respectively, where u

and u

are as pictured in Fig. 7.4.

However, it must be noted that such an example as (7.59) is exceptional. A real

elastic substance would tend to have a potential energy function F.v/ that in-

creases much more rapidly for large (or even moderate) v. A speciﬁc example is

(7.60)

F.v/ D

1  v

C v; K.v/ D

.1  v/

C 1;

.v/ D

.1  v/

.v/ D6





.1  v/



;

on  Df.v; w/ W 0<v<1g. In this case, the system (7.14) is genuinely

nonlinear except on the line fv D 1=2g.

Another situation giving rise to (7.11) is a model of a string, vibrating in R

but (magically) constrained to have only transverse vibrations, so a point whose

coordinate on the string is x is at the point



x; V.t; x/



2 R

at time t.Insucha

case,  D R

and F.v/ has the form F.v/ D f.v

/,so

K.v/ D 2f

/v:

Thus K.v/ is a smooth odd function on R. Hence K

is also odd and must vanish

at v D 0. Thus genuine nonlinearity must fail at v D 0. We will return to this a

little later; see (7.85)–(7.91).

We next investigate how Proposition 7.1 applies to the equations of isentropic

compressible ﬂuid ﬂow, in the form (7.8), which can be cast in the form

(7.61)

 w

D 0;

 K.v; w/

D 0;

a generalization of the form (7.14), if we set

(7.62) v D ; w Dm; K.v; w/ D

C p.v/:

(This v is not the v in (7.5).) For smooth solutions, (7.61) takes the form (7.2)

with

(7.63) A.u/ D





7. Systems of conservation laws in one space variable; Riemann problems 483

This has eigenvalues and eigenvectors

(7.64) 

D

C 4K







With K.v; w/ given by (7.62), we have

(7.65) 



./;

which is equivalent to (7.10). In this case,

(7.66) r

r

D˙

./



./ C

./





D˙

A

.3/=2

;

the last identity holding when p./ D A



,asin(7.6). Thus the system (7.8)is

genuinely nonlinear in the region  Df.; m/ W >0g.

A number of important cases of Riemann problems are not covered by

Proposition 7.1. We will take a look at some of them here, though our treat-

ment will not be nearly exhaustive.

First, we consider a condition that is directly opposite to the hypothesis of

genuine nonlinearity. We say the j th ﬁeld is linearly degenerate provided

(7.67) r

.u/ r

.u/ D 0 on :

In such a case, the integral curve of R

D r

rthrough u

, which we denote

now by '

I/ instead of (7.23), does not produce a set of data u

for which

there is a rarefaction wave solution to (7.17), of the form (7.18)–(7.20), but we do

have the following.

Lemma 7.2. Under the linear degeneracy hypothesis (7.67), if we set

(7.68) s D 

and let u

D '

I/ for any  (for which the ﬂow is deﬁned), then

(7.69)

u.t; x/ D u

; for x<st;

; for x>st

deﬁnes for t  0 a weak solution to the Riemann problem (7.17); that is, the

Rankine–Hugoniot condition (7.29) is satisﬁed. Furthermore,

(7.70) 

/ D s:

484 16. Nonlinear Hyperbolic Equations

Proof. Setting './ D '

I/,wehave

(7.71) '

./ D r



'./



.0/ D u

By the deﬁnition of r

, this implies

(7.72)





'./



 



'./



./ D 0:

Now the Rankine–Hugoniot condition (7.29)foru

D './, with s D 

holds for all  if and only if

(7.73)

d



'./



 

/'./

D 0;

or equivalently,

(7.74)





'./



 



./ D 0:

On the other hand,

d





'./



D '

./ r



'./



D r



'./



r



'./



D 0;

(7.75) 



'./



D 

/ D s; 8 :

This implies (7.70) and also shows that the left sides of (7.72)and(7.74) are equal,

so the lemma is proved.

When the j th ﬁeld is linearly degenerate, the weak solution to the Riemann

problem deﬁned by (7.69) is called a contact discontinuity. The term “contact”

refers to the identity (7.70), that is, to

(7.76) 

/ D s D 

which contrasts with the shock condition (7.52). Note that in deﬁning '

I/,

we do not restrict  to be  0,asforaj -shock curve, nor do we restrict  to be

 0,asforaj -rarefaction curve. Rather,  runs over an interval containing 0 in

its interior.

There is a straightforward extension of Proposition 7.1:

Proposition 7.3. Assume that the L  L system (7.1) is strictly hyperbolic and

that each ﬁeld is either genuinely nonlinear or linearly degenerate. Given u

2 ,

there is a neighborhood O of u

such that if u

2 O, then there is a weak solution

to (7.1) with initial data

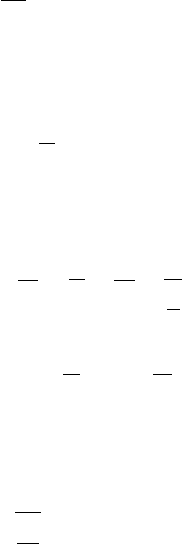
7. Systems of conservation laws in one space variable; Riemann problems 485

(7.77)

u.0; x/ D u

; for x<0;

; for x>0;

consisting of a set of rarefaction waves, shock waves satisfying the Lax condition

(7.52), and contact discontinuities.

An important example is the following system:

(7.78)



C .v/

D 0;

.v/

C .v

C p.; S/

D 0;

.S /

C .Sv/

D 0;

for a one-dimensional compressible ﬂuid that is not isentropic; here S.t;x/ is the

“entropy,” and the equation of state p D p./ is generalized to p D p.; S/.

Compare with (5.61)–(5.62). Using m D v as before, we can write this system

(7.79)



C m

D 0;





C p.; S/



D 0;

.S /

C .mS /

D 0:

Note that, for smooth solutions, we can replace the last equation by

(7.80) S



D 0:

In this case, we have u D .;m;S/and

(7.81)

A.u/ D

010





@



010

v

@

00v

Note that A.u/ leaves invariant the two-dimensional space f.a;b;0/g,soasin

(7.10) we have eigenvalues and eigenvectors

(7.82) 

D v ˙

@

D .1; 

;0/

486 16. Nonlinear Hyperbolic Equations

Also, by inspection A.u/

has eigenvector .0;0;1/

, with eigenvalue v,which

must also be an eigenvalue of A.u/;wehave

(7.83) 

D v D





1; v; 









; 





Thus

(7.84) r

r

D







D 0:

Of course r

r

are still given by (7.66). Thus we have one linearly degenerate

ﬁeld and two genuinely nonlinear ﬁelds for the 3  3 system (7.79).

In  10 we will see that the study of a string vibrating in a plane gives rise to a

4  4 system that, in some cases, has two linearly degenerate ﬁelds and two gen-

uinely nonlinear ﬁelds, though for such a system there are also more complicated

possibilities.

We now return to the 2  2 system (7.14), i.e.,

(7.85)

 w

D 0;

 K.v/

D 0;

in cases such as those mentioned after (7.60), that is,

(7.86) K.v/ D 2f

/v;

where  D R

and f

is smooth, with f

.0/ > 0. Thus, as computed before, we

have

(7.87) 

D˙

D .1; 

r

D˙

1=2

;

or, with the ˙ subscript replaced by j I˙1 D .1/

;jD 1; 2,

(7.88) R



D .1/

1=2

The genuine nonlinearity condition fails on the line v D 0. We will assume that

is behaved so that K

>0on R;K

>0on .0; 1/, K

<0on .1;0/,

and K

vvv

.0/ > 0.Set

(7.89) 

Df.v; w/ W˙R



>0g;

so in the case we are considering, the regions 

are pictured in Fig. 7.6.

In Fig. 7.7 we depict the various shock and rarefaction curves emanating from

on the left and those emanating from u

on the right. The rarefaction curves,

which are integral cuves of R

, terminate upon hitting the vertical axis fv D 0g.

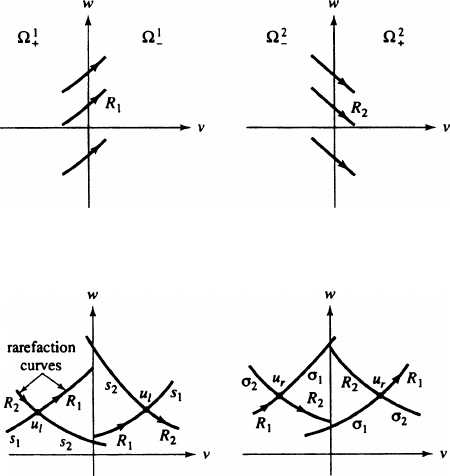
7. Systems of conservation laws in one space variable; Riemann problems 487

FIGURE 7.6 The Regions 

FIGURE 7.7 Rarefaction and Shock Curves Through u

and u

On the other hand, the shock curves continue to produce solutions to the Riemann

problem even after they cross this axis, though the Lax shock conditions might

break down eventually. Note that the rarefaction curves from u

are ﬂow-outs of

in 

and ﬂow-outs of R

in 



We look at the question of how to solve the Riemann problem when u

cannot

be connected to curves that avoid the vertical axis v D 0.

In Fig. 7.8 we indicate in one case how to extend the curve '

I/ for posi-

tive , beyond the point where this curve (which initially, for >0,isanintegral

curve of R

) intersects the vertical axis.

To decide precisely which u

lie on this continued curve, it is easiest to work

backward from u

, along the shock curve 

, continued across the vertical axis

into the region fv<0g.Letu

denote the ﬁrst point along 

at which the Lax

shock condition fails. Thus the solution to the Riemann problem with initial data

for x<0;u

for x>0, has a one-sided contact discontinuity, in the sense

that the speed s satisﬁes

(7.90) 

/ D s<

Then the ﬂow-out from u

under R

gives rise to u

that are connected to u

a solution such as that indicated in Fig. 7.9.

Thus the solution consists of a rarefaction wave connecting u

to u

, followed

by a jump discontinuity that is a one-sided contact and one-sided shock, as stated

in (7.90).