Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

458 16. Nonlinear Hyperbolic Equations

for t  0; x 2 T

D M , as limits of solutions u



(6.2)



D u



/; u



.0/ D f:

This method of producing solutions to (6.1) is called the viscosity method. Recall

from Proposition 1.5 of Chap. 15 that, for each >0;f 2 L

.M /,(6.2)hasa

unique global solution



2 L

.Œ0; 1/  M/\ C

..0; 1/  M/;

with

(6.3) ku



.t/k

kf k

;

for each t  0, and furthermore if u

j

solve (6.2) with u

j

D f

, then, for each

t>0,

(6.4) ku

1

.t/  u

2

.t/k

kf

 f

;

by Proposition 1.6 in that section. We will use these facts to show that as  & 0;



g has a limit point u solving (6.1), provided f 2 L

.M / \ BV.M/,where,

with M.M / denoting the space of ﬁnite Borel measures on M ,

(6.5) BV.M/ Dfu 2 D

.M / Wru 2 M.M /g:

As shown in Chap. 13,  1, BV.M/  L

n=.n1/

.M /. Of course, that BV  L

for n D 1 is a standard result in introductory measure theory courses. Our analysis

begins with the following:

Lemma 6.1. If f 2 BV.M/ and u



solves (6.2), then

(6.6) fu



W  2 .0; 1g is bounded in L

;BV/:

Proof. If we deﬁne 

f.x/ D f.xC y/, it is clear that

(6.7) f 2 BV H) kf  

f k

 C jyj;

for jyj1=2. Now apply (6.4) with f

D f; f

D 

f to obtain, for each t  0,

(6.8) ku



.t/  



.t/k

 C jyj;

which yields (6.6).

Now if we write @



/ D F



, and note the boundedness in the

sup norm of F



/, we deduce that

6. Weak solutions to scalar conservation laws; the viscosity method 459

(6.9) f@



/ W  2 .0; 1g is bounded in L

; M.M //:

Let us use the inclusion

(6.10) M.M /  H

ı;p

.M /; p

ı>n;

a consequence of Sobolev’s imbedding theorem, which implies

(6.11) BV.M/  H

1ı;p

.M /:

We think of choosing ı small and p close to 1. We deduce from (6.6)and(6.9)that

fuC



/gis bounded in L

1ı;p

.M //, and hence, by (6.2),

(6.12) f@



g is bounded in L

1ı;p

Thus, for t;t

>0,

(6.13) ku



.t/  u



1ı;p

.M /

 C jt  t

with C independent of  2 .0; 1. We now use the following interpolation in-

equality, a special case of results established in Chap. 13:

kvk

";p

 C kvk

1

1ı;p

kvk



1ı;p

;

where  2 .0; 1/ and " D .1  /.1  ı/ C .1  ı/ D 1  2  ı C ı is

>0if  is chosen small and positive. We apply this to (6.13) and the following

consequence of (6.6)and(6.11):

(6.14) ku



.t/  u



1ı;p

 C;

to conclude that, for some >0;">0,

(6.15) fu



g is bounded in C



.Œ0; T ; H

";p

.M //;

for all T<1; hence, by Ascoli’s theorem,

(6.16) fu



g is compact in C.Œ0; T ; L

.M //;

for all T<1.

From here, producing a limit point u solving (6.1) is easy. Given T<1,by

(6.16) we can pass to a subsequence 

! 0 such that

(6.17) u



D u

! u in C.Œ0; T ; L

.M //I

460 16. Nonlinear Hyperbolic Equations

by a diagonal argument we can arrange this to hold for all T<1. We can also

assume u

.t; x/ ! u.t; x/ pointwise a.e. on R

 M . In view of the pointwise

boundedness (6.3), we deduce

(6.18) F

/ ! F

.u/ in L

.Œ0; T   M/;

as k !1, for each T . Hence we have weak convergence:

(6.19)

;

u

! 0; @

/ ! @

.u/;

implying that u solves (6.1). We summarize:

Proposition 6.2. Given f 2 L

.M / \BV.M/, the solutions u



to (6.2) have a

weak limit point

(6.20) u 2 C.Œ0;1/; L

.M // \ L

 M/\ L

; BV .M //;

for all p<1, solving (6.1).

As we will see below, weak solutions to (6.1) in the class (6.20) need not be

unique. However, there is uniqueness for those solutions obtained by the viscosity

method. A device that provides a proof of this, together with an intrinsic char-

acterization of these viscosity solutions, is furnished by “entropy inequalities,”

which we now discuss.

Let  W R ! R be any C

-convex function (so 

>0). Note that, for v D

v.t; x/; @

.v/ D 

.v/ @

v and @

.v/ D 

.v/ @

v C 

.v/.@

,so

.v/ D 

.v/v C 

.v/jr

Thus, if u



solves (6.2), and if we multiply each side by 



/, we obtain

(6.21)

.u



/ D .u



/  



/jru



where, using 

.v/ @

.v/ D 

.v/F

.v/ @

v and @

.v/ D q

.v/ @

v,we

require of q

that

(6.22) q

.v/ D 

.v/F

.v/:

Now, for u



! u as above, we have derived weak convergence .u



/ !

.u/ and, by the same reasoning, q



/ ! q

.u/, but we have no basis to

say that jru



!jruj

, and in fact this convergence can fail (otherwise the

inequality we derive would always be an equality). Taking this into account, we

abstract from (6.21) the inequality

6. Weak solutions to scalar conservation laws; the viscosity method 461

(6.23)

.u



/ 



/  .u



using convexity of , and then, passing to the limit u



! u, obtain

(6.24)

.u/ 

.u/  0;

in the sense that we have a nonpositive measure on .0; 1/  M on the left side.

In other words,

(6.25) ' 2 C



.0; 1/  M



;' 0;

implies

(6.26)

“





u.t; x/







u.t; x/



dx dt  0:

By a limiting argument, we can let .u/ tend to ju  kj, for any given k 2 R,

and use q

.u/ D sgn.u  k/ŒF

.u/  F

.k/, to deduce (using the summation

convention)

(6.27)

“

ju kj'

 sgn.u  k/



.u/  F

.k/



dx dt  0;

for all ' satisfying (6.25). That (6.27) holds for all k 2 R is called Kruzhkov’s

entropy condition. The following is Kruzhkov’s key result:

Proposition 6.3. If u and v belong to the space in (6.20) and both satisfy Kruzh-

kov’s entropy condition, and if u.0; x/ D f.x/; v.0;x/ D g.x/, then, for t>0,

ku.t/  v.t/k

kf gk

:(6.28)

Proof. Let us write the entropy condition for v in the form (using the summation

convention)

(6.29)

“

jv  `j'

 sgn.v  `/



.v/  F

.`/



dy ds  0;

for all ` 2 R.Let' D '.s; t; x; y/ be smooth and compactly supported in

s>0;t>0,and'  0. Now substitute v.s;y/ for k in (6.27), u.t; x/ for `

in (6.29), integrate both over dx dy ds dt, and sum, to get

(6.30)

ZZZZ

u.t; x/  v.s; y/

C '

/  sgn



u.t; x/ v.s;y/







.u/  F

.v/





o

dx dy ds dt  0:

462 16. Nonlinear Hyperbolic Equations

We now consider the following functions ':

(6.31) '.s;t; x; y/ D f.t/d

.t  s/ı

.x  y/;

where f; d

;ı

 0 and, as h ! 0; d

and ı

approach the delta functions on R

and T

D M , respectively. With such a choice, note that @'=@x

C@'=@y

D 0

and '

C '

D f

.t/d

.t  s/ı

.x  y/. Passing to the limit h ! 0 yields

(6.32)

“

u.t; x/ v.t; x/

.t/ dx dt  0;

for all nonnegative f 2 C



.0; 1/



, which in turn implies

(6.33)

ku.t/  v.t/k

 0;

yielding (6.28).

We have given all the arguments necessary to establish the following:

Corollary 6.4. Given f 2 L

.M / \ BV.M/, the weak solutions to (6.1)be-

longing to the space (6.20) which are limits of solutions u



to (6.2) are unique.

Given two such f

, initial data for viscosity solutions u

, we have

(6.34) ku

.t/  u

.t/k

kf

 f

;

for t  0. Furthermore, a weak solution to (6.1) is a viscosity solution if and only

if the entropy inequality (6.27) holds for all k 2 R.

As a complementary remark, we note that if u, belonging to (6.20), satisﬁes

Kruzhkov’s entropy condition, then automatically u is a weak solution to (6.1).

Indeed, let v be the viscosity solution with the same initial data as u;by(6.28),

v D u.

Note that (6.27) can be rewritten as

(6.35)

“

ju  kj



.u;k/

dx dt  0;

where G

.u;k/ D ŒF

.u/  F

.k/=.u  k/ is smooth in its arguments. The

formula (6.30) can be similarly rewritten; also, (6.32) can be generalized to

(6.36)

“

u.t; x/ v.t; x/



.u;v/

dx dt  0;

for a pair u;v satisfying Kruzhkov’s entropy condition. Suppose their initial data

are bounded in sup norm by M , which therefore bounds u.t/ and v.t/ for all

t  0;pickA so that

6. Weak solutions to scalar conservation laws; the viscosity method 463

(6.37) juj; jvjM H)

.u;v/

 A

Now pick '.t; x/ D f.t/ .t;x/, with f as above and satisfying

(6.38)

C Ajr

j0;

so that

(6.39)

.u;v/jj@

j0:

Then (6.36) implies

(6.40)

“

u.t; x/  v.t; x/

.t/ .t; x/ dx dt  0:

By a limiting argument, we can let be the characteristic function of a set in

Œ0; 1/  T

of the form

(6.41) f.t; x/ Wjx  x

jB  Atg:

Then, reﬁning (6.33), we deduce that

(6.42)

jxx

jBAt

u.t; x/ v.t; x/

dx D D.t/ & as t % :

In particular, if u.0; x/ D v.0; x/ on fx Wjx x

jBg, we deduce the following

result on ﬁnite propagation speed:

Proposition 6.5. If u and v are viscosity solutions to (6.1), bounded by M , with

initial data f and g which agree on a set fx Wjx  x

jBg, and if A is large

enough that (6.37) holds, then u and v coincide on the set (6.41).

In light of this, we have in a natural fashion unique, global entropy-satisfying

weak solutions to (6.1), for t  0; x 2 R

, provided the initial data belong to

/ and have bounded variation.

We next consider weak solutions to (6.1) with discontinuities of the simplest

sort; namely, we suppose that u.t; x/ is deﬁned for t  0; x 2 R, and that there

is a smooth curve  ,givenbyx D x.t/, such that u.t; x/ is smooth on either side

of , with a simple jump across .If.x; t/ 2 , denote by Œu D Œu.x; t / the size

of this jump:

(6.43) Œu D lim

"&0

u.x.t/ C "; t/  u.x.t/  "; t/:

464 16. Nonlinear Hyperbolic Equations

If F W R ! R is smooth, we let ŒF  denote the jump in F.u/ across  .Now,if

such u solves

(6.44) u

C F.u/

D 0



R



n , then this object on R

R will be a measure supported on I u

will be a weak solution everywhere provided this measure vanishes. It is a simple

exercise to evaluate this measure in terms of the jumps Œu and ŒF  and the slope

of , or equivalently the speed s D dx=dt, as being proportional to sŒu  ŒF .In

other words, such a u provides a weak solution to (6.44) precisely when

(6.45) sŒu D ŒF  on :

This condition is called the jump condition, or the Rankine–Hugoniot condition.

A special case of solutions to (6.44)off are functions u that are piecewise

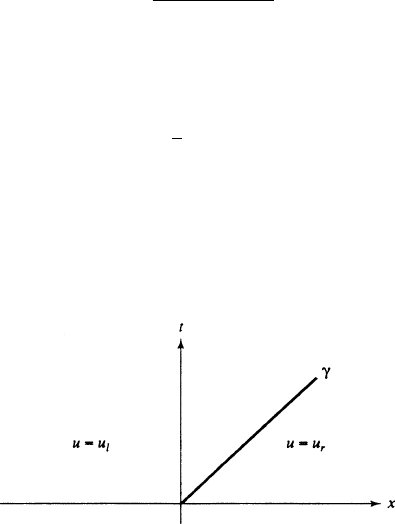
constant. Thus the jumps are constant, so s is constant, so  is a line; we may

as well call it the line x D st (possibly shifting the origin on the x-axis). See

Fig. 6.1.Ifu D u

on the left side of  and u D u

on the right side of  ,the

Rankine–Hugoniot condition becomes

(6.46) s D

F.u

/  F.u

 u

An initial-value problem with such piecewise-constant initial data is called a Rie-

mann problem. Let us describe two explicit weak solutions to

(6.47) u





D 0

of this form, in Fig. 6.2.

Claim 6.6. Figure 6.2A describes an entropy-satisfying solution of (6.47), while

Fig. 6.2B describes an entropy-violating solution.

FIGURE 6.1 Shock Wave

6. Weak solutions to scalar conservation laws; the viscosity method 465

FIGURE 6.2 Entropy Satisfaction and Violation

In each ﬁgure we have drawn in integral curves of the vector ﬁelds @=@t C

.u/.@=@x/ in the regions where u is smooth. Note that in Fig. 6.2A these curves

run into , while in Fig. 6.2B these curves diverge from .

These assertions are consequences of the following result of Oleinik:

Proposition 6.7. Let u.t; x/ be a piecewise smooth solution to (6.44)onR



R with jump across  , satisfying the jump condition (6.45). Then the entropy

condition holds if and only if

(i) in case u

< u

The graph of y D F.u/ over Œu

; u

 lies below the chord connecting the point



;F.u





;F.u



;

(ii) in case u

> u

The graph of y D F.u/ over Œu

; u

 lies above the chord.

These two cases are illustrated in Fig. 6.3. A weak solution to (6.44)which

satisﬁes the hypotheses of Proposition 6.7 is said to satisfy Oleinik’s “condition

(E).”

Proof. As a slight variation on Kruzhkov’s convex functions, it sufﬁces to con-

sider the weakly convex functions

.u/ D 0; for u <k;

u  k; for u >k;

FIGURE 6.3 Oleinik’s Condition (E)

466 16. Nonlinear Hyperbolic Equations

plugged into the inequality 

C q

 0, with

q.u/ D 0; for u <k;

F.u/  F.k/; for u >k;

as k runs over R. In fact only for k between u

and u

is 

nonzero; in such

a case it is a measure supported on ,whichis 0 if and only if



.u

/  .u



 F.u

/  F.u

The jump condition (6.46)ons then implies

(6.48) F.k/ 

 k

 u

F.u

/ C

k  u

 u

F.u

for k between u

and u

, which is equivalent to the content of (i)–(ii).

Note that if F is convex (i.e., F

>0), as in the example (6.47), then the

content of (i) and (ii) is

(6.49) F

/>s>F

/.for F

>0/;

a result that, for F.u/ D u

=2, holds in the situation of Fig. 6.2A but not in that

of Fig. 6.2B.

For weak solutions to (6.1) with these simple discontinuities, if the entropy

conditions are satisﬁed, the discontinuities are called shock waves. Thus the dis-

continuity depicted in Fig. 6.2A is a shock, but the one in Fig. 6.2B is not.

The Riemann problem for (6.47) with initial data u

D 0; u

D 1, has an

entropy-satisfying solution, different from that of Fig. 6.2B, which can be ob-

tained as a special case of the following construction. Namely, we look for a

piecewise smooth solution of (6.44), with initial data u.0; x/ D u

for x<0;u

for x>0, and which is Lipschitz continuous for t>0, in the form

(6.50) u.t; x/ D v.t

1

x/:

The PDE (6.44) yields for v the ODE

(6.51) v

.s/



.v.s//  s



D 0:

We look for v.s/ Lipschitz on R, satisfying alternatively v

.s/ D 0 and

.v.s// D s on subintervals of R, such that v.1/ D u

and v.C1/ D u

Let us suppose that F.u/ is convex (F

>0)foru between u

and u

and that

the shock condition (6.49) is violated (i.e., we suppose u

< u

). Since F

.u/ is

monotone increasing on u

 u  u

, we can deﬁne an inverse map D .F

1

G W ŒF

/; F

/ ! Œu

; u

:

6. Weak solutions to scalar conservation laws; the viscosity method 467

FIGURE 6.4 Rarefaction Wave

Then setting

(6.52) v.s/ D

; for s<F

G.s/; for F

/  s  F

; for s>F

completes the construction. For the PDE (6.47), with F

.u/ D u, the solution so

produced is illustrated in Fig. 6.4. There is a fan of lines through .0; 0/ drawn in

this ﬁgure, with speeds s running from 0 to 1,andu D s on the line with speed

dx=dt D s.

Solutions to (6.44) constructed in this fashion are called rarefaction waves.

If F is concave between u

and u

, an analogous construction works, provided

> u

Rarefaction waves always satisfy the entropy conditions, since if u is a weak

solution to (6.44), .u/

C q.u/

D 0 on any open set on which u is Lipschitz.

In case F.u/ is either convex or concave over all of R, any Riemann problem

for (6.44) has an entropy-satisfying solution, which is either a shock wave or a

rarefaction wave. In these two respective cases we say u

is connected to u

a shock wave or by a rarefaction wave. If F

.u/ changes sign, there are other

possibilities. We illustrate one here; let u

< u

,andsayF.u/ is as depicted in

Fig. 6.5 (with an inﬂection point at v

FIGURE 6.5 More Complex Nonlinearity