Taylor M.E. Partial Differential Equations III: Nonlinear Equations
Подождите немного. Документ загружается.

468 16. Nonlinear Hyperbolic Equations
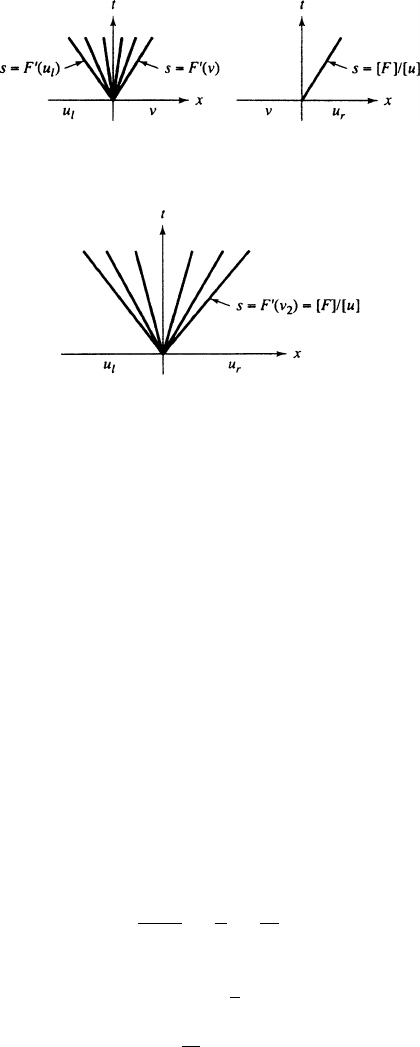
FIGURE 6.6 Rarefaction and Shock
FIGURE 6.7 Rarefaction Bounded by a Shock
By the analysis above, we see that if v
1
v v
2
, we can connect u
`
to v
by a rarefaction wave, and we can connect v and u
r
by a shock, as illustrated in
Fig. 6.6.
These can be fitted together provided ŒF .v/ F.u
r
/=.v u
r
/ F
0
.v/.This
requires v D v
2
, so the solution is realized by a rarefaction wave bordered by a
shock, as illustrated in Fig. 6.7.
We now illustrate the entropy solution to u
t
C.1=2/.u
2
/
x
D 0 with initial data
equal to the characteristic function of an interval, namely,
(6.53)
u.0; x/ D 1; for 0 x 1;
0 otherwise:
For 0 t 2, this solution is a straightforward amalgamation of the
rarefaction wave of Fig. 6.4 and the shock wave of Fig. 6.2A. For t>2,thereisan
interaction of the rarefaction wave and the shock wave. Let
x./; t./
denote a
point on the shock front (for t 2)whereu D .FromŒu D ; ŒF D
2
=2,
and s D ŒF =Œu D =2, we deduce
x
0
./
t
0
./
D
2
D
x
2t
:
Hence x
0
=x D t
0
=2t,sologx D .1=2/ log t C C ,orx D kt
1=2
.Sincex D 2 at
t D 2 on the shock front, this gives k D
p
2. Thus the shock front is given by
(6.54) x D
p
2t; for t 2:

Exercises 469
FIGURE 6.8 Curved Shock Front
This is illustrated in Fig. 6.8. Note that the interaction of these waves leads to
decay:
(6.55) sup
x
u.t; x/ D
r
2
t
; for t 2:
Exercises
Exercises 1–3 examine a difference scheme approximation to (6.1), used by [CwS]and
[Kot]. Let h D t; " D x
j
,andletƒ be the n-dimensional lattice
ƒ Dfx 2 R
n
W x D "˛; ˛ 2 Z
n
g:
We want to approximate a solution u.t; x/ to (6.1)att D hk; x D "˛,byu.k; ˛/,
defined on Z
C
ƒ, satisfying the difference scheme
(6.56)
1
h
"
u.k C 1; ˛/
1
2n
n
X
j D1
n
u
k; ˛ C ı.j /
C u
k; ˛ ı.j /
o
#
C
1
2"
n
X
j D1
n
F
j
u.k; ˛ C ı.j //
F
j
u.k; ˛ ı.j //
o
D 0;
for k 0, with initial condition
(6.57) u.0; ˛/ D f.˛/:
Here, ı.j/ D .0;:::;1;:::;0/, with the 1 in the j th position. We impose the “stability
condition”
(6.58) 0<h
"
An
;AD max
j
sup
jwjM
jF
0
j
.w/j:
470 16. Nonlinear Hyperbolic Equations
1. Show that
(6.59) sup
˛
jf.˛/jM H) j u.k; ˛/jM:
(Hint: Write F
j
u.k; ˛ C ı.j //
F
j
u.k; ˛ ı.j //
D ˆ
k˛j
u.k; ˛ C ı.j //
u.k; ˛ ı.j //
. Then rewrite (6.56)as
(6.60)
u.k C 1; ˛/ D
1
2n
n
X
j D1
n
u
k; ˛ C ı.j /
C u
k; ˛ ı.j /
o
h
2"
n
X
j D1
ˆ
k˛j
n
u
k; ˛ C ı.j /
u
k; ˛ ı.j /
o
:
Hence
u.k C 1; ˛/ D
X
ˇ2ƒ
k˛ˇ
u.k; ˇ/;
where
P
ˇ
k˛ˇ
D1, and, given (6.58),
k˛ˇ
0. Deduce that ju.k C 1; ˛/j
sup
ˇ
ju.k; ˇ/j:)
2. If v.k;˛/ solves (6.56) with v.0; ˛/ D g.˛/, show that
(6.61)
X
˛2ƒ
ˇ
ˇ
u.k; ˛/ v.k;˛/
ˇ
ˇ
X
˛2ƒ
ˇ
ˇ
f.˛/ g.˛/
ˇ
ˇ
:
Compare with (6.4). Deduce that
(6.62)
n
X
j D1
X
˛2ƒ
ˇ
ˇ
u
k; ˛
u
k; ˛ C ı.j /
ˇ
ˇ
n
X
j D1
X
˛2ƒ
ˇ
ˇ
f.˛/ f
˛ C ı.j /
ˇ
ˇ
:
(Hint: With w.k;˛/ D u.k; ˛/ v.k; ˛/, deduce from (6.56)that
(6.63)
w.k C 1; ˛/ D
1
2n
n
X
j D1
n
w
k; ˛ C ı.j /
C w
k; ˛ ı.j /
o
h
2"
n
X
j D1
n
‰
k;˛Cı.j/
w
k; ˛ C ı.j /
‰
k;˛ı.j /
w
k; ˛ ı.j /
o
;
where F
j
u.k; ˛/
F
j
v.k;˛/
D‰
k˛
w
k; ˛
. Multiply (6.63)by
k˛
D sgn w
.k C 1; ˛/ and sum over ˛,toget
X
˛
jw.k C 1; ˛/jD
X
˛
k˛
w.k;˛/;
where
k˛
D
1
2n
X
j
n
1
nh
"
‰
k˛
k;˛ı.j /
C
1 C
nh
"
‰
k˛
k;˛Cı.j/
o
:
Using 1 ˙ .nh="/‰
k˛
0, deduce that 1
k˛
1:)

Exercises 471
3. Show that
(6.64)
X
˛
h
1
ˇ
ˇ
u.k C 1; ˛/ u.k; ˛/
ˇ
ˇ
A
n
X
j D1
X
˛2ƒ
"
1
ˇ
ˇ
f
˛ C ı.j /
f.˛/
ˇ
ˇ
C
1
2n
"
2
h
n
X
j D1
X
˛2ƒ
"
2
ˇ
ˇ
f
˛ C ı.j /
2f .˛/ C f
˛ ı.j /
ˇ
ˇ
:
(Hint:Setv.k; ˛/ D u.k C 1; ˛/, and apply (6.61). Then use (6.56)toanalyze
u.1; ˛/ f.˛/.)
Let us use the notation
(6.65)
t
u.k; ˛/ D
1
h
"
u.k C 1; ˛/
1
2n
n
X
j D1
n
u
k; ˛ C ı.j /
C u
k; ˛ ı.j /
o
#
;
j
v.k;˛/ D
1
2"
h
v
k; ˛ C ı.j /
v
k; ˛ ı.j /
i
;
so (6.56) takes the form
(6.66)
t
u C
n
X
j D1
j
F
j
.u/ D 0:
The following is a special case of a result in [L4].
4. Let and q
j
be as in (6.22). Assume
0<m
00
.u/ M<1;
and strengthen (6.58)to
h
"
An
r
1 C
m
M
1
:
Show that a solution u to (6.66) also satisfies
(6.67)
t
.u/ C
X
j
j
q
j
.u/ 0:
Compare with (6.24).
5. Let u
.t; x/ be the entropy solution to u
t
C .1=2/.u
2
/
x
D 0 with initial data
u
.0; x/ D
1
; for 0 x ;
0 otherwise:
Compare u
to the solution to (6.53), illustrated in Fig. 6.8.
Note that, given 0<<1,wehaveu
.t; x/ D u
1
.t; x/ for large t,sothereisno
backward uniqueness.
Show that as ! 0; u
! u
0
, depicted in Fig. 6.9. Show that u
0
is an entropy solution
of
u
t
C
1
2
.u
2
/
x
D 0; u.0; x/ D ı.x/:

472 16. Nonlinear Hyperbolic Equations
FIGURE 6.9 Solution with Initial Data ı.x/
7. Systems of conservation laws in one space variable;
Riemann problems
Here we consider L L first-order systems of the form
(7.1) u
t
C F.u/
x
D 0;
where x belongs to either R or S
1
D R=Z. Here, u takes values in R
L
, or perhaps
in some region R
L
,andF W ! R
L
is smooth. Assume is simply
connected. If u is a smooth solution of (7.1), then
(7.2) u
t
C A.u/u
x
D 0; A.u/ D D
u
F.u/:
Thus A.u/ is an L L matrix. We typically make the hypothesis of strict hyper-
bolicity, that A.u/ has L real and distinct eigenvalues:
(7.3) A.u/r
j
.u/ D
j
.u/r
j
.u/;
1
.u/<<
L
.u/:
The vectors r
j
.u/ 2 R
L
are eigenvectors of A.u/.
The equation (7.1)issaidtobeasystemofconservation laws because, if
u.t; x/ either vanishes sufficiently rapidly as x !˙1or is defined for x 2 S
1
,
then
(7.4)
Z
u.t; x/ dx D C
is independent of t; thus the components of this vector are conserved quantities.
To see this, using (7.1), we have
d
dt
Z
u.t; x/ dx D
Z
F.u/
x
dx D 0;

7. Systems of conservation laws in one space variable; Riemann problems 473
by the fundamental theorem of calculus. As we will see in 8,(7.1) will
sometimes give rise to other “conservation laws” for u.
We give a couple of examples of systems of conservation laws. First consider
equations of isentropic compressible fluid flow. When x 2 R
n
and n D 1,then
the system (2.11) for compressible fluid flow specializes to
(7.5)
v
t
C vv
x
D
p
x
;
t
C v
x
C v
x
D 0:
We assume p D p./ is a given function of , the most common relation being
(7.6) p./ D A
; A>0; 1<<2;
as in (2.12). We can rewrite (7.5) in conservation form:
(7.7)
v
t
C
1
2
v
2
C q./
x
D 0;
t
C .v/
x
D 0;
where q
0
./ D p
0
./=.Ifp./ is given by (7.6), we can take
q./ D
A
1
1
:
Alternatively, we can set m D v, the momentum density, and rewrite (7.5)as
(7.8)
t
C m
x
D 0;
m
t
C
m
2
C p
x
D 0:
In this case, we have u D .; m/ and
(7.9) A.u/ D
01
m
2
2
C p
0
./
2m
!
D
01
v
2
C p
0
./ 2v
;
which has eigenvalues and eigenvectors:
(7.10)
˙
D v ˙
p
p
0
./; r
˙
D
1
˙
:
As a second example, consider this second-order equation, for real-valued V :
(7.11) V
tt
K.V
x
/
x
D 0;

474 16. Nonlinear Hyperbolic Equations
which is a special case of (3.12). As discussed in 1 of Chap. 2, this equation
arises as the stationary condition for an action integral
(7.12) J.V / D
“
h
1
2
V
2
t
F.V
x
/
i
dx dt:
Here, F.V
x
/ is the potential energy density. Thus K.v/ has the form
K.v/ D F
0
.v/:
If we set
(7.13) v D V
x
;wD V
t
;
we get the 2 2 system
(7.14)
v
t
w
x
D 0;
w
t
K.v/
x
D 0:
In this case, u D .v; w/ and
(7.15) A.u/ D
0 1
K
v
0
;K
v
D F
00
.v/:
We assume F
00
.v/ > 0.Then(7.14) is strictly hyperbolic; A.u/ has eigenvalues
and eigenvectors
(7.16)
˙
D˙
p
K
v
;r
˙
D
1
˙
:
As in the scalar case examined in 6, we expect classical solutions to (7.1)to
break down, and we hope to extend these to weak solutions, with shocks, and so
forth. Our next goal is to study the Riemann problem for (7.1),
(7.17)
u.0; x/ D u
`
; for x<0;
u
r
; for x>0;
given u
`
; u
r
2 R
L
, and try to obtain a solution in terms of shocks and rarefaction
waves, extending the material of (6.43)–(6.52).
We first consider rarefaction waves, solutions to (7.1) of the form
(7.18) u.t; x/ D '.t
1
x/;
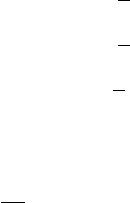
7. Systems of conservation laws in one space variable; Riemann problems 475
for '.s/ which is Lipschitz and piecewise smooth. Now u
t
D.x=t
2
/'
0
.x=t/
and u
x
D .1=t/'.x=t/,so(7.2) implies
(7.19)
A.'.s// s
'
0
.s/ D 0:
Thus, on any open interval where '
0
.s/ ¤ 0, we need, for some j 2f1;:::;Lg,
(7.20)
j
'.s/
D s; '
0
.s/ D ˛
j
.s/r
j
'.s/
;
where r
j
.u/ is the
j
-eigenvector of A.u/ and ˛
j
.s/ is real-valued. Differentiat-
ing the first of these identities and using the second, we have
(7.21) ˛
j
.s/ r
j
'.s/
r
j
'.s/
D 1:
We say that (7.1) is genuinely nonlinear in the j th field if r
j
.u/ r
j
.u/ is
nowhere zero (on the domain of definition, R
L
). Granted the condition of
genuine nonlinearity, one typically rescales the eigenvector r
j
.u/,sothat
(7.22) r
j
.u/ r
j
.u/ D 1:
Then (7.20) holds with ˛
j
.s/ D 1.
Consequently, if (7.1) is genuinely nonlinear in the j th field and u
`
2 R
L
is
given, then there is a smooth curve in R
L
, with one endpoint at u
`
, called the
j -rarefaction curve:
(7.23) '
r
j
.u
`
I/; 0
j
;
for some
j
>0,sothat
(7.24) '
r
j
.u
`
I0/ D u
`
;
and, for any 2 .0;
j
/, the function u defined by
(7.25) u.t; x/ D
8
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
:
u
`
; for
x
t
<
j
.u
`
/;
'
r
j
.u
`
I/; for
x
t
D 2
j
.u
`
/;
j
'
r
j
.u
`
I/
;
'
r
j
.u
`
I/ D u
r
; for
x
t
>
j
.u
r
/
is a j -rarefaction wave. See Fig. 7.1. Note that given (7.22), we have
(7.26)
d
d
'
r
j
.u
`
I0/ D r
j
.u
`
/:
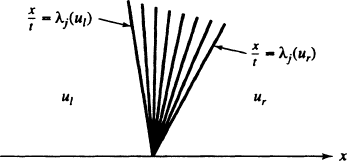
476 16. Nonlinear Hyperbolic Equations
FIGURE 7.1 J-Rarefaction Wave
Next we consider weak solutions to (7.1) of the form
(7.27)
u.t; x/ D u
`
; for x<st;
u
r
; for x>st;
for t>0,givens 2 R, the “shock speed.” As in (6.45), the condition that this
define a weak solution to (7.1)istheRankine–Hugoniot condition:
(7.28) sŒu D ŒF ;
where Œu and ŒF are the jumps in these quantities across the line x D st;inother
words,
(7.29) F.u
r
/ F.u
`
/ D s.u
r
u
`
/:
If course, if L>1, unlike in (6.46), we cannot simply divide by u
r
u
`
;the
identity (7.29) now implies the nontrivial relation that the vector F.u
r
/F.u
`
/ 2
R
L
be parallel to u
r
u
`
. We will produce curves '
s
j
.u
`
I/, smooth on 2
.
j
;0,forsome
j
>0,sothat
(7.30) '
s
j
.u
`
I0/ D u
`
;
and, for any 2 .
j
;0, the function u defined by (7.27) is a weak solution to
(7.1), with
(7.31) u
r
D '
s
j
.u
`
I/; s D s
j
./;
where s
j
./ is also smooth on .
j
;0. For notational convenience, set './ D
'
s
j
.u
`
I/. Thus we want
(7.32) F
'./
F.u
`
/ D s
j
./
'./ u
`
:
If this holds, then taking the -derivative yields
(7.33)
A
'./
s
j
./
'
0
./ D s
0
j
./
'./ u
`
:
7. Systems of conservation laws in one space variable; Riemann problems 477
If this holds, setting D 0 gives
(7.34)
A.u
`
/ s
j
.0/
'
0
.0/ D 0;
so
(7.35) s
j
.0/ D
j
.u
`
/;
and '
0
.0/ is proportional to r
j
.u
`
/. Reparameterizing in ,if'
0
.0/ ¤ 0, we can
assume
(7.36) '
0
.0/ D r
j
.u
`
/:
We now show that such a smooth curve './ exists. Guided by (7.36), we set
(7.37) './ D u
`
C r
j
.u
`
/ C ./
and show that, for close to 0, there exists ./ 2 R
L
near 0, such that (7.33)
holds. We will require that ./ 2 V
j
, the linear span of the eigenvectors of A.u
`
/
other than r
j
.u
`
/. Then we want to solve for 2 V
j
;2 R:
(7.38)
1
F.u
`
C r
j
.u
`
/ C / F.u
`
/
j
.u
`
/ C
r
j
.u
`
/ C
D 0:
Denote the left side by ˆ
,so
(7.39) ˆ
W O R ! R
L
;
where O is a neighborhood of 0 in V
j
. This extends smoothly to D 0, with
(7.40)
ˆ
0
.; / D A.u
`
/
r
j
.u
`
/ C
j
.u
`
/ C
r
j
.u
`
/ C
D
A.u
`
/
j
.u
`
/
r
j
.u
`
/:
Note that ˆ
0
.0; 0/ D 0.Also,
(7.41) Dˆ
0
.0; 0/
D
A.u
`
/
j
.u
`
/
r
j
.u
`
/;
which is an invertible linear map of V
j
˚R ! R
L
. The inverse function theorem
implies that, at least for close to 0, ˆ
./;./
D 0 for a uniquely defined
smooth
./;./
satisfying .0/ D 0; .0/ D 0.
We see that the curve './ is defined on a two-sided neighborhood of D 0,
but, taking a cue from 6, we will restrict this to 0 to define the j -shock
curve '
s
j
.u
`
I/. Comparing (7.36) with (7.26), we see that '
s
j
.u
`
I/ and the j -
rarefaction curve '
r
j
.u
`
I/ fit together to form a C
1
-curve, for 2 .
j
;
j
/;we
denote this curve by '
j
.u
`
I/.
