Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

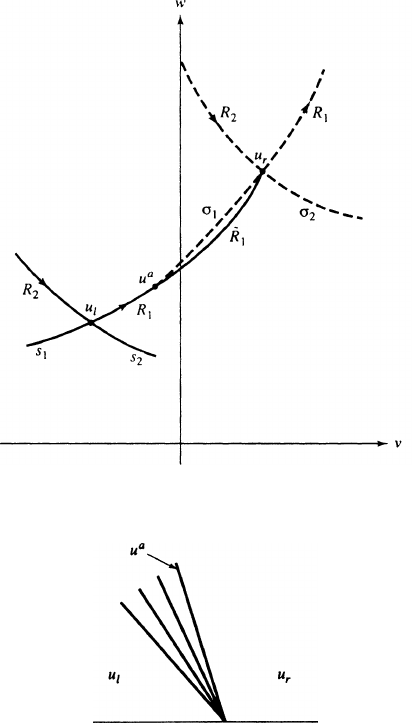
488 16. Nonlinear Hyperbolic Equations

FIGURE 7.8 Connecting u

to u

FIGURE 7.9 One-Sided Contact Discontinuity

In Fig. 7.10, we take the case illustrated by Fig. 7.8 and relabel the old u

,takinganewu

, connected to u

by S

[

, consisting of the shock curve

out of u

, continued beyond the vertical axis until the Lax shock condition fails,

at u

, and then followed by the ﬂow-out from u

under R

The resulting solution to the Riemann problem is depicted in Fig. 7.11.First

we have the 1-rarefaction connecting u

to u

, followed by the jump disconti-

nuity connecting u

to u

,asinFig.7.9. Then we have the jump discontinuity

connecting u

to u

, satisfying the shock/contact condition

(7.91) 

/<sD 

Finally, u

is connected to u

by a 2-rarefaction.

7. Systems of conservation laws in one space variable; Riemann problems 489

FIGURE 7.10 Connecting u

to u

FIGURE 7.11 Two One-Sided Contacts

Figures 7.9 and 7.11 should remind one of Fig. 6.7, depicting the solution to a

Riemann problem for a scalar conservation law, satisfying Oleinik’s condition (E).

In fact, it can be veriﬁed that the discontinuities produced by the construction

above satisfy the following admissibility condition. Say a weak solution to (7.85)

is equal to .v

/ for x<stand to .v

/ for x>st;t 0. Then the

admissibility condition is that, for all v between v

and v

, either

(7.92)

K.v/  K.v

v  v



K.v

/  K.v

 v

.if s  0/;

(7.93)

K.v/  K.v

v  v



K.v

/  K.v

 v

.if s  0/:

Compare this to the formulation (6.48) of condition (E).

490 16. Nonlinear Hyperbolic Equations

In [Liu1] there is a treatment of a class of 2  2 systems, containing the case

just described, in which an extension of condition (E) is derived. See also [Wen].

This study is extended to n  n systems in [Liu2].

Further interesting phenomena for the Riemann problem arise when there is

breakdown of strict hyperbolicity. Material on this can be found in [KK2, SS2],

and in the collection of articles in [KK3]. We will not go into such results here,

though some mention will be made in  10.

In addition to solving the Riemann problem when u

and u

are close, one also

wants solutions, when possible, when u

and u

are far apart. There are a number

of results along these lines, which can be found in [DD,KK1,Liu2,SJ]. We restrict

our discussion of this to a single example.

We give an example, from [LS], of a strictly hyperbolic, genuinely nonlinear

system for which the Riemann problem is solvable for arbitrary u

; u

2 ,but

some of the solutions do not ﬁt into the framework of Proposition 7.1. Namely,

consider the 2  2 system (7.5)–(7.6) describing compressible ﬂuid ﬂow, for u D

.v; /, with  Df.v; / W >0g. As seen in (7.10), if we switch to .m; /-

coordinates, with m D v, then there are eigenvalues 

D m= ˙

./

and eigenvectors R

D @=@ C 

@=@m. Thus integral curves of R

satisfy

P D 1; Pm D m= ˙

./; hence

Pv D

Pm  m P



D˙

./



;

that is, integral curves of R

through .v

;

/ are given by

(7.94) v  v

D˙



.s/

ds D˙

A



.3/=2

ds:

If  2 .1; 2/,asassumedin(7.6), then these rarefaction curves intersect the axis

 D 0. Note that if we normalize R

so that R



D 1,then

(7.95) R



A



3



1=2

./



@

Furthermore, specializing (7.58), we see that the shock curves from u

are

given by

(7.96) v  v

D



  





p./  p.





1=2

; for ˙ .

 / > 0:

Note that these shock curves never reach the axis  D 0.SeeFig.7.12 for a picture

of the shock and rarefaction curves emanating from u

Now, as in Fig. 7.13,picku

D .v

;

/ 2  and consider the “triangular”

region T , with apex at u

, bounded by the integral curves of R



(forward) and

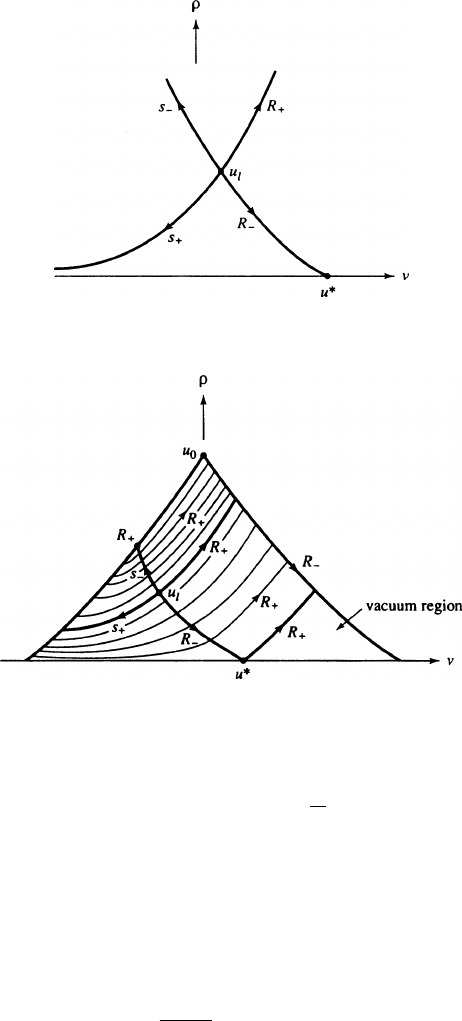
7. Systems of conservation laws in one space variable; Riemann problems 491

FIGURE 7.12 Shock and Rarefaction Curves Through u

FIGURE 7.13 Vacuum Region

of R

(backward) through u

, and by the axis  D 0. This is a bounded region.

Given any u

; u

2 T , we will produce a solution to the Riemann problem, whose

intermediate state also belongs to T (oratleastto

T ).

In fact, as seen in Fig. 7.13,ifu

2 T , the rarefaction and shock waves de-

scribed before sufﬁce to do this for u

in all of T except for a smaller triangular

region in the lower right corner of T , which we call the “vacuum region.” This

is bounded by part of @T , plus part of the integral curve of R

emanating from



,whereu



is the point of intersection of the R



-integral curve through u

with

f D 0g.

What we do if u

belongs to this vacuum region is indicated in Figs. 7.14 and

7.15. Namely, u

is connected to the vacuum by a rarefaction wave, whose speed

on the left is 



/ D v



.

/ and whose speed on the right is 





/ D







;0/ D v



(since p

.0/ D 0 when (7.6) holds). Next, if u

D .v

;0/is the

point on the axis f D 0g from which issues the R

-integral curve through u

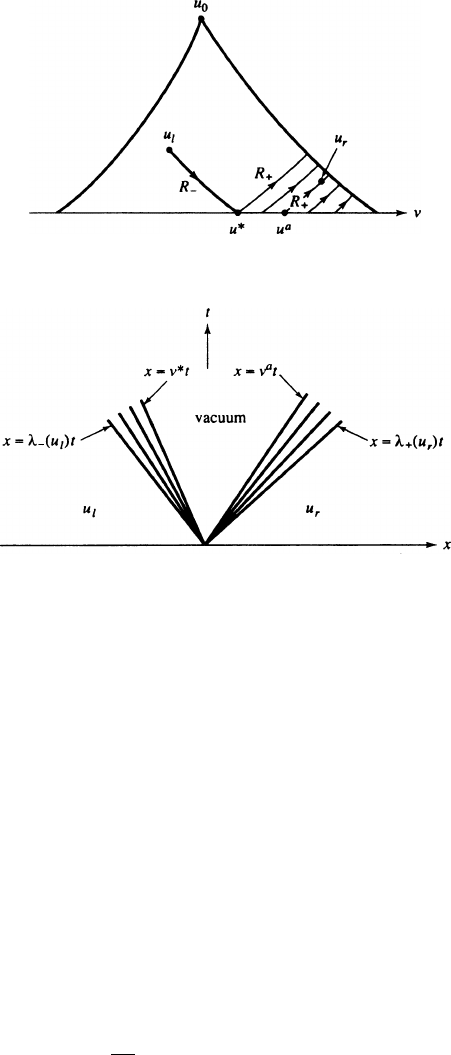
492 16. Nonlinear Hyperbolic Equations

FIGURE 7.14 Connecting u

to u

Through the Vacuum

FIGURE 7.15 Associated Solution to the Riemann Problem

then the vacuum is connected to u

by a rarefaction wave whose speed on the left

is 

/ D v



(if u

¤ u



) and whose speed on the right is 

/.Inthe

special case that u

D u



, the vacuum state disappears, except for a single ray,

along which the two rarefaction waves ﬁt together.

This concludes our discussion in this section of examples of the Riemann prob-

lem. In  10 there is further discussion for equations of vibrating strings.

Continuing a theme from  6, we next explore the relation between the shock

condition (7.52) and the possibility that the solution u is a limit as " & 0 of

solutions to

(7.97) @

C @

F.u

/ D "@

Here, we will look for solutions to (7.97) of the form

(7.98) u

.t; x/ D v



1

.x  ct/



This satisﬁes (7.97) if and only if

(7.99)

d



F.v/ cv./



D v

./;

7. Systems of conservation laws in one space variable; Riemann problems 493

or equivalently, if and only if there exist b 2 R

such that

(7.100) v

./ D F.v/ cv  b D ˆ

.v/:

In other words, v./ should be an integral curve of the vector ﬁeld ˆ

.There-

quirement that the limit u.t; x/ satisfy the Riemann problem (7.17) is equivalent to

v.1/ D u

;v.C1/ D u

:(7.101)

Consequently, u

and u

should be critical points of the vector ﬁeld ˆ

, con-

nected by a “heteroclinic orbit.” If this happens, we say u

is connected to u

via

a “viscous proﬁle.”

For u

and u

to be critical points of ˆ

, we need

(7.102) F.u

/  cu

D b D F.u

/  cu

;

hence

(7.103) F.u

/  F.u

/ D c.u

 u

This is precisely the Rankine–Hugoniot condition (7.29), with s D c. Now, con-

sider the behavior of the vector ﬁeld ˆ

near each of these critical points. The

linearization near u

D u

or u

is given by

(7.104) V.u

C v/ D



A.u

/  s



Now, if (7.52) holds (i.e., 

/<s<

/), and if u

and u

are sufﬁciently

close, then A.u

/  s has L  .j  1/ positive eigenvalues and j  1 negative

eigenvalues, while A.u

/s has Lj positive eigenvalues and j negative eigen-

values.

The qualitative theory of ODE guarantees the existence of a heteroclinic orbit

from u

to u

(if they are sufﬁciently close). We will not give the proof here, but

conﬁne our discussion to a presentation of Fig. 7.16, illustrating the 2  2 case

in which u

is connected to u

by a 1-shock. The ODE theory involved here has

been developed quite far, in order also to investigate cases where u

and u

are not

close but can still be shown to be connected by a viscous proﬁle. The book [Smo]

gives a detailed discussion of this.

We mention a variant of the viscosity method described above, which was used

in [DD]. Namely, we look at a family of solutions to

(7.105) @

C @

F.u

/ D "t @

of the form

(7.106) u

.t; x/ D v

1

x/;

494 16. Nonlinear Hyperbolic Equations

FIGURE 7.16 Forcing a Heteroclinic Orbit

where v

./ solves

(7.107) "v

./ D



A.v

/  



./;

and

(7.108) v

.1/ D u

.C1/ D u

Setting w

./ D v

./,wegeta.2L/.2L/ ﬁrst-order system for V

D .v

(7.109) V

./ D ‰



; V

./





./; "

1

ŒA.v

/  w

./



;

with

(7.110) V

.1/ D .u

;0/; V

.C1/ D .u

;0/:

The paper [DD] considered such solutions when (7.1)isa2 2 system, satisfying

(7.111)

<0;

<0; 8 u 2 R

;

a condition that guarantees strict hyperbolicity. In particular, it is shown in [DD]

that this viscosity method leads to a solution to the Riemann problem for all data

; u

/ whenever (7.1) is a symmetric hyperbolic 22 system, satisfying (7.111).

We mention another “viscosity method” that has been applied to 2 2 systems

of the form (7.14). Namely, for ">0, consider

(7.112)

 w

D 0;

 K.v/

D "v

7. Systems of conservation laws in one space variable; Riemann problems 495

This comes via v D u

;wD u

, from the equation

(7.113) u

 K.u

D "u

xxt

;

which arises in the study of viscoelastic bars; see [Sh1]and[Sl]. We look for

a traveling wave solution U D .v; w/ of the form U



.x  st/="



, satisfying

U.1/ D .v

/; U.C1/ D .v

/. Thus we require

(7.114)

s.v v

/  .w  w

/ D 0;

s.w  w

/ 



K.v/  K.v



Dsv

./;

hence

(7.115) sv

./ D K.v/  K.v

/  s

.v  v

/I v.1/ D v

;v.C1/ D v

For this to be possible, one requires that .v/ D K.v/  K.v

/  s

.v  v

vanish at v D v

as well as v D v

; this together with the ﬁrst part of (7.114)

constitutes precisely the Rankine–Hugoniot condition, that

U D .v

/ for x<

st; .v

/ for x>st;t 0, be a weak solution to (7.14). In addition, in order to

solve (7.115), one requires that v

be a source for the vector ﬁeld .sgn s/ .v/@=@v

on R,thatv

be a sink, and that there be no other zeros of .v/ for v between v

and v

. Thus we require

K.v/  K.v

v  v

 s

>0;

for v between v

and v

< if s>0, and the reverse inequality if s<0. Note that

this implies the admissibility condition (7.92)–(7.93),given that K.v

/K.v

/ D

 v

/. See the exercises after  8 for more on this viscosity method.

There is a method for approximating a solution to (9.1) with general initial

data, via solving a sequence of Riemann problems, called the Glimm scheme,after

[Gl1], where it is used as a tool to establish the existence of global solutions for

certain classes of initial-value problems. The method is the following: Divide the

x-axis into intervals J



of length `. In each interval J



, pick a point x



, at random,

evaluate u.0; x



/ D a



, and now consider the piecewise-constant initial data so

obtained. Assuming, for example, that (8.1) is strictly hyperbolic and genuinely

nonlinear, and ju.0; x/jC , one can obtain for small h a weak solution v.t; x/ to

(8.1)on.t; x/ 2 Œ0; h  R, consisting locally of solutions to Riemann problems;

see Fig. 7.17. Now, pick a new sequence y



of random points in J



,evaluate

v.h; y



/ D b



, and repeat this construction to deﬁne v.t; x/ for .t; x/ 2 Œh; 2h 

R. Continue. In [Gl1] there are results giving conditions under which one has

v D v

`;h

well deﬁned for .t; x/ 2 R

 R, and convergent to a weak solution as

` ! 0; h D c

`. Further results can be found in [GL, DiP1, Liu5]; see also the

treatment in [Smo]. In  9 we will describe a different method, due to [DiP4], to

establish global existence for a class of systems of conservation laws.

496 16. Nonlinear Hyperbolic Equations

FIGURE 7.17 Setup for Glimm’s Scheme

Exercises

In Exercises 1–3, we consider some shock interaction problems for a system of the

form (7.1). Assume (7.1)isa2 2 sysyem, strictly hyperbolic and genuinely nonlinear.

Assume u

and u

are sufﬁciently close together.

1. Suppose that, for t<t

; u takes three constant values, u

; u

, in regions separated

by shocks of the opposite family, with shock speeds s



. Assume the faster shock is

to the left. Thus these shocks must intersect; say they do so at t D t

(see Fig. 7.18).

Show that the solution to the Riemann problem at t D t

, with data u

; u

, consists

of two shocks, s



, as depicted in Fig. 7.18. In particular, there are no rarefaction

waves.

2. Suppose that, for t<t

; u takes on three constant values u

; u

, in regions sepa-

rated by shocks of the same family, say s

, and assume that the left shock has higher

speed than the right shock. Thus these two shocks must intersect; say they do so at

t D t

(see Fig. 7.19). Show that the solution to the Riemann problem at t D t

, with

data u

; u

, consists of a shock of the same family as those that interacted, together

(perhaps) with either a shock wave or a rarefaction wave of the other family. (Hint:

Study Fig. 7.4.)

If only the second possibility can occur when two shocks of the same family collide,

the 2 2 system is said to satisfy the “shock interaction condition.” This condition was

introduced by Glimm and Lax; see [GL].

3. Show that the shock interaction condition holds, at least for sufﬁciently weak shocks,

provided that  D R

and, for each u

2 , the curves '

I/ and '

I/ are

FIGURE 7.18 Situation for Exercise 1

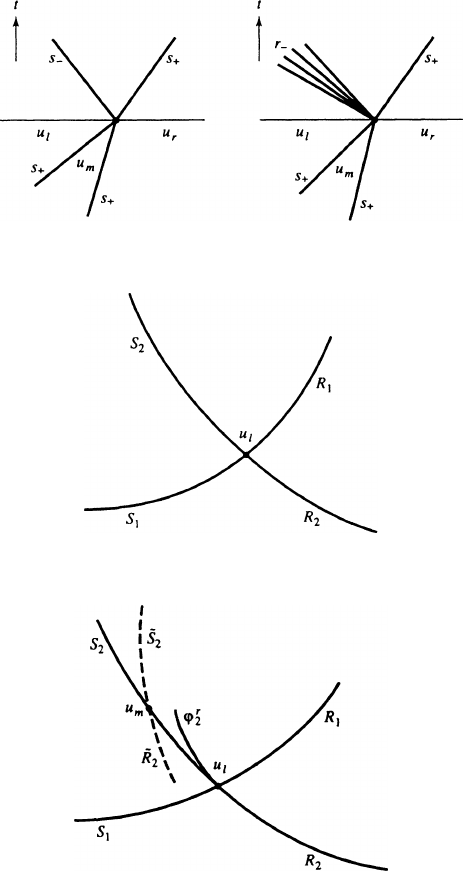
Exercises 497

FIGURE 7.19 Situation for Exercise 2

FIGURE 7.20 Situation for Exercise 3

FIGURE 7.21 Possible Attack on Exercise 3

both strongly convex, as in Fig. 7.20. Here, '

I/ is obtained by piecing together

the rarefaction curve '

I/ and the shock curve '

I/.(Hint: Show that if, for

example, u

lies on the 2-shock curve from u

,asinFig.7.21, then the 2-wave curve

I/ D

[

is as pictured in that ﬁgure, as is the continuation of '

I/

for <0. To do this, you will need to look at @



I˙0/.See[SJ].)