Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.


The basic idea used in Stiles’ method and the Dykstra–Parsons method is to
determine the frontal position in each layer at the time water breakthrough
occurs in successive layers. If the flow capacity of each layer is defined by
the product of permeability and thickness, i.e., kh, then the water and oil flow
rates from all layers can be calculated to yield the producing water–oil ratio.
Stiles’ Method
Stiles (1949) proposed an approach that takes into account the effect of
permeability variations in predicting the performance of waterfloods.
Stiles assumes that in a layered system, the water breakthrough occurs in
a sequence that starts in the layer with the highest permeability. Assum-
ing that the reservoir is divided into n layers that are arranged in a
descending permeability order with breakthrough occurring in a layer i,
all layers from 1 to i have already been swept by water. The remaining
layers obviously have not reached breakthrough.
Based on the above concept, Stiles proposed that the vertical sweep
efficiency can be calculated from the following expression:
where i = breakthrough layer, i.e., i = 1,2,3, . . . n
n = total number of layers
E
V
= vertical sweep efficiency
h
t
= total thickness, ft
h
i
= layer thickness, ft
If the values of the porosity vary between layers, Equation 14-90 can be
written:
Stiles also developed the following expression for determining the sur-
face water–oil ratio as breakthrough occurs in any layer:
E
k
hkh
k
h
V
i
j
j
ji
n
j
i
i
j
j
n
=
(
)
+
(
)
(
)
(
)
=+=
=
∑∑
∑
φ
φ
φ
φ
11
1
14 - 91
E
kh kh
kh
V
ij
j
ji
n
j
i
it
=
+
(
)
(
)
=+=
∑∑
11
14 - 90
998 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 998

with
where WOR
s
= surface water–oil ratio, STB/STB
k
rw
= relative permeability to water at S
or
k
ro
= relative permeability to oil at S
wi
Both the vertical sweep efficiency and surface WOR equations are used
simultaneously to describe the sequential breakthrough as it occurs in
layer 1 through layer n. It is usually convenient to represent the results of
these calculations graphically in terms of log(WOR
s
) as a function of E
V
.
Example 14-21
The Dykstra and Parsons (1950) permeability ordering approach is used
to describe a reservoir by the following five-layer system:
Layer k, md h, ft
1 120 15
29015
37010
45510
53010
The reservoir is under consideration for further development by water
injection. The following additional information is available:
k
rw
@S
or
= 0.3
k
ro
@S
wi
= 0.9
o
= 2.0 cp
w
= 0.5 cp
B
o
= 1.20 bbl/STB
B
w
= 1.01 bbl/STB
h
t
= 60 ft
A
k
k
B
B
rw
ro
oo
ww
=
(
)
µ
µ
14 - 93
WOR A
kh
kh
s
j
j
i
j
ji
n
=
(
)
(
)
(
)
=
=+
∑
∑
1
1
14 - 92
Principles of Waterflooding 999
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 999

Calculate the vertical sweep efficiency and surface water-oil ratio using
Stiles’ method:
Solution
Step 1. Calculate parameter A using Equation 14-93:
Step 2. Calculate E
V
and WOR
s
when breakthrough occurs in the first
layer, i.e.,
i = 1, by applying Equations 14-90 and 14-92:
WOR
kh
kh
WOR
kh
kh kh kh kh
WOR
STB STB
s
j
j
j
j
s
s
=
=
+++
=
+++
=
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
=
=
∑
∑
1 584
1 584
1 584
120 15
90 15 70 10 55 10 30 10
0 983
1
1
2
5
1
2345
.
.
.
./
E
kh kh
kh
E
kh kh kh k h kh
kh
E
V
ij
j
i
j
j
it
V
it
V
=
(
)
=
++++
[]
=
(
)
(
)
+
(
)
(
)
+
(
)
(
)
+
(
)
(
)
+
(
)
(
)
[]
(
)
(
)
=
==
∑∑
12
5
11 2 2 3 3 4 4
55
120 15 90 15 70 10 55 10 30 10
120 60
0 653.
A =
(
)
(
)
(
)
(
)
=
03
09
20 120
05 101
1 584
.
.
..
..
.
1000 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1000

Step 3. Calculate E
V
and WOR
s
when water breakthrough occurs in the
second layer, i.e., i = 2:
Step 4. The required calculations can be performed more conveniently in
the following worksheet:
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
Layer k
i
h
i
∑h
i
k
i
∑h
i
k
i
h
i
∑k
i
h
i
h
t
k
i
1 120 15 15 1,800 1,800 1,800 7,200 0.653 0.983
2 90 15 30 2,700 1,350 3,150 5,400 0.787 3.22
3 70 10 40 2,800 700 3,850 4,200 0.869 7.17
4 55 10 50 2,750 550 4,400 3,300 0.924 23.23
5 30 10 60 1,800 300 4,700 1,800 1.000 —
sum = 4700
WOR
sm
s
=
-
1 584
7
7
.
(())
(())
E
sum
V
=
++57
8
(())(())
[[]]
WOR
kh
kh
WOR
kh kh
kh kh kh
WOR STB STB
s
j
j
j
j
s
s
=
(
)
(
)
(
)
=
(
)
(
)
+
(
)
(
)
+
(
)
+
(
)
=
(
)
(
)
(
)
+
(
)
(
)
(
)
(
)
+
(
)
(
)
+
(
)
(
)
=
=
=
∑
∑
1 584
1 584
1 584
120 15 90 15
70 10 55 10 30 10
322
1
2
3
5
12
345
.
.
../
E
kh kh
kh
E
kh h kh kh kh
kh
E
V
j
j
j
j
t
V
t
V
=
+
(
)
=
+
(
)
+
(
)
+
(
)
+
(
)
[]
=
+
(
)
+
(
)
(
)
+
(
)
(
)
+
(
)
(
)
[]
(
)
(
)
=
==
∑∑
2
1
2
3
5
2
21 2
345
2
90 15 15 70 10 55 10 30 10
90 60
0 787.
Principles of Waterflooding 1001
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1001
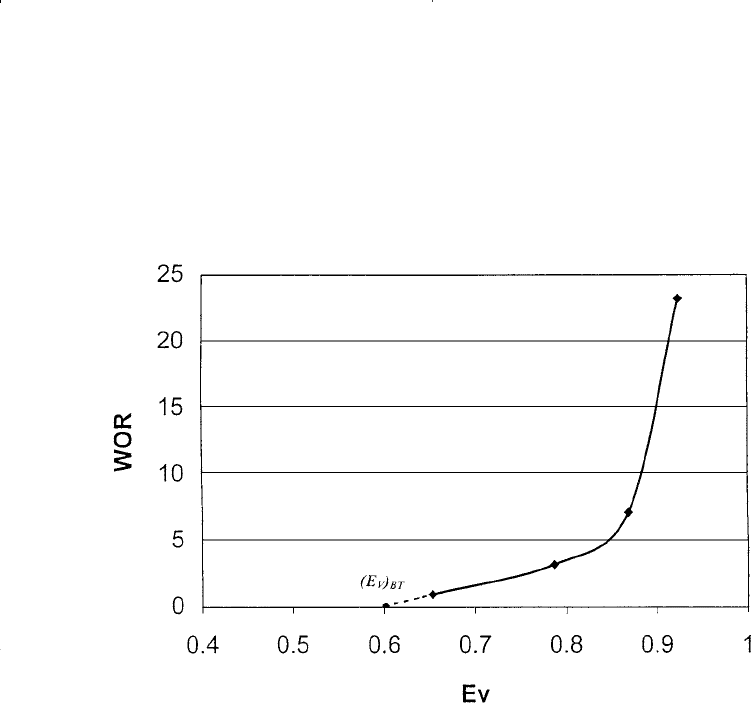
Figure 14-51 shows the resulting relationship between the vertical sweep
efficiency and producing WOR. The curve can be extended to WOR = 0
to give the vertical sweep efficiency at breakthrough E
V
.
Figure 14-51. WOR vs. E
v
.
The Dykstra–Parsons Method
Dykstra and Parsons (1950) correlated the vertical sweep efficiency
with the following parameters:
• Permeability variation V
• Mobility ratio M
• Water–oil ratio WOR
r
as expressed in bbl/bbl
The authors presented their correlation in a graphical form for water–oil
ratios of 0.1, 0.2, 0.5, 1, 2, 5, 10, 25, 50, and 100 bbl/bbl. Figure 14-52
shows Dykstra and Parsons’ graphical correlation for a WOR of 50
bbl/bbl. Using a regression analysis model, de Souza and Brigham (1981)
1002 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1002

grouped the vertical sweep efficiency curves for 0 ≤ M ≤ 10 and 0.3 ≤ V
≤ 0.8 into one curve as shown in Figure 14-53. The authors used a com-
bination of WOR, V, and M to define the correlation parameter Y of Fig-
ure 14-53:
with
Figure 14-52. Vertical sweep efficiency curves for WOR = 50. (Permission to pub-
lish by the Society of Petroleum Engineers.)
0.0
0.2
0.4
0.6
0.8
1.0
0.0 0.2 0.4
Vertical sweep efficiency
0.6 0.8 1.0
PERMEABILITY VARIATION, V
WOR = 50 BBL PER BBL
100
50
30
20
10
0.5
0.2
1.0
2
3
4
5
M = 0.1
xVV=+−
(
)
1 6453 0 935 0 6891
2
... 14 - 95
Y
WOR V
MV
x
=
+
(
)
−
(
)
−+
(
)
(
)
0 4 18 948 2 499
0 8094 1 137 10
.. .
..
14 - 94
Principles of Waterflooding 1003
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1003
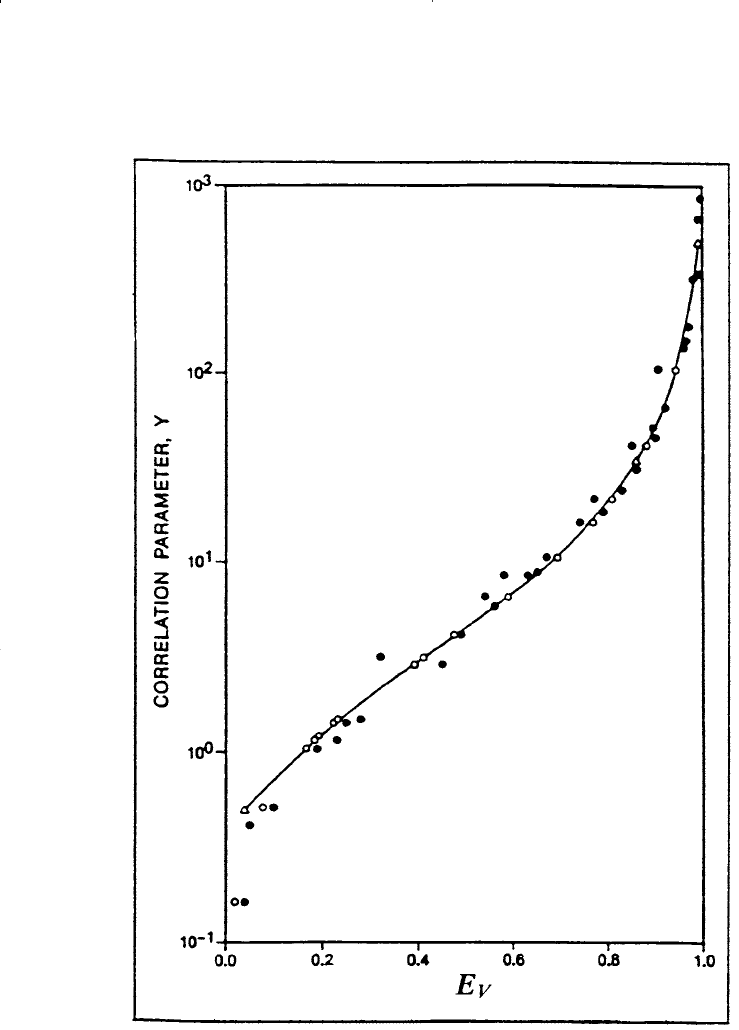
Figure 14-53. E
V
versus the correlating parameter Y. (Permission to publish by
the Society of Petroleum Engineers.)
1004 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1004

The specific steps involved in determining the vertical sweep efficien-
cy as a function of water–oil ratios are summarized below:
1. Calculate the mobility ratio M and permeability variation V.
2. Select several values for the WOR, e.g., 1, 2, 5, 10, and calculate the
correlating parameter Y at each selected WOR.
3. Enter Figure 14-53 with each value of Y and determine the corre-
sponding values of the vertical sweep efficiency E
V
.
4. Plot WOR versus E
V
.
To further simplify the calculations for determining E
V
, Fassihi (1986)
curve-fitted the graph of Figure 14-53 and proposed the following non-
linear function, which can be solved iteratively for the vertical sweep
efficiency E
V
:
where a
1
= 3.334088568
a
2
= 0.7737348199
a
3
= 1.225859406
The Newton–Raphson method is perhaps the appropriate technique for
solving Equation 14-96. To avoid the iterative process, the following
expression could be used to estimate the vertical sweep efficiency using
the correlating parameter Y:
With the coefficients a
1
through a
6
as given by:
a
1
= 0.19862608 a
2
= 0.18147754
a
3
= 0.01609715 a
4
= –4.6226385 × 10
–3
a
5
= –4.2968246 × 10
–4
a
6
= 2.7688363 × 10
–4
Example 14-22
A layered reservoir is characterized by a permeability variation V of
0.8. Calculate the vertical sweep efficiency E
V
when the producing
water–oil ratio reaches 50 bbl/bbl assuming a mobility ratio of 10.0.
Eaa Ya Y a Y a YaY
V
=+
(
)
+
(
)
[]
+
(
)
[]
+
(
)
+
12 3
2
4
3
5
6
ln ln ln / ln
aE E Y
V
a
V
a
1
2
3
10−
(
)
−=
(
)
14 - 96
Principles of Waterflooding 1005
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1005

Solution
Step 1. Calculate the parameter x by applying Equation 14-95:
Step 2. Calculate the correlation parameter Y from Equation 14-96:
Step 3. From Figure 14-53, determine E
V
to give:
METHODS OF PREDICTING RECOVERY
PERFORMANCE FOR LAYERED RESERVOIRS
To account for the reservoir vertical heterogeneity when predicting
reservoir performance, the reservoir is represented by a series of layers
with no vertical communication, i.e., no cross-flow between layers. Each
layer is characterized by a thickness h, permeability k, and porosity φ.
The heterogeneity of the entire reservoir is usually described by the per-
meability variation parameter V. Three of the methods that are designed
to predict the performance of layered reservoirs are discussed below.
Simplified Dykstra–Parsons Method
Dykstra and Parsons (1950) proposed a correlation for predicting
waterflood oil recovery that uses the mobility ratio, permeability varia-
tion, and producing water–oil ratio as correlating parameters. Johnson
(1956) developed a simplified graphical approach for the Dykstra and
Parsons method that is based on predicting the overall oil recovery R at
water–oil ratios of 1, 5, 25, and 100 bbl/bbl. Figure 14-54 shows the pro-
posed graphical charts for the four selected WOR
s
. The correlating para-
meters shown in Figure 14-54, are:
R = overall oil recovery factor
S
wi
= initial water saturation
M = mobility ratio
V = permeability variation
E
V
= 056.
Y =
+
(
)
−
(
)
[]
−
(
)
+
[]
=
50 0 4 18 948 2 499 0 8
10 0 8094 0 8 1 137 10
5 863
1 1427
.. . .
...
.
.
x =
(
)
+
(
)
−=1 6453 0 8 0 9735 0 8 0 6891 1 1427
2
..... .
1006 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1006
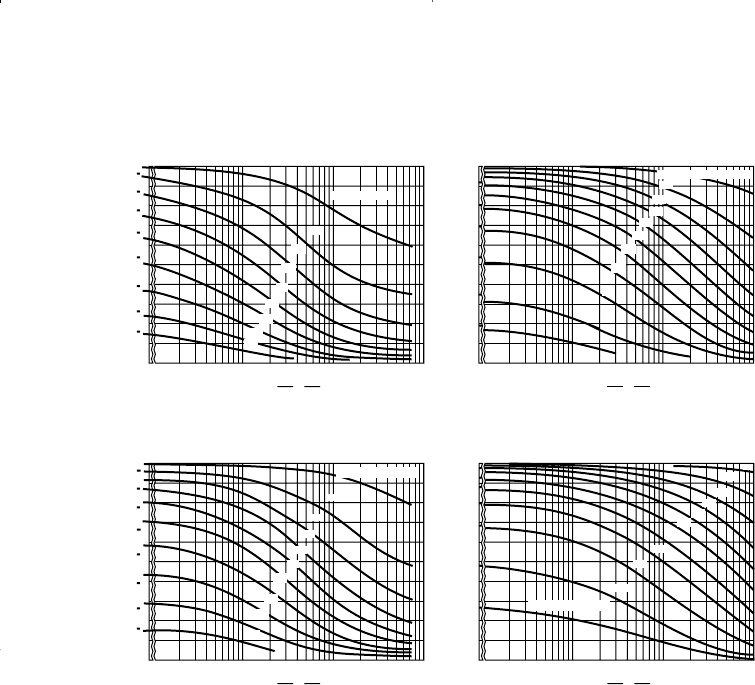
Figure 14-54. Simplified Dykstra and Parsons curves. (Permission to publish by
the Society of Petroleum Engineers.)
The practical application of the simplified Dykstra and Parsons
method is outlined below:
1. Calculate the permeability variation V and mobility ratio M.
2. Using the permeability ratio and mobility ratio, calculate the overall
oil recovery factor R from the four charts at WOR of 1, 5, 25, 100
bbl/bbl. For example, to determine the oil recovery factor when the
WOR reaches 5 bbl/bbl for a flood pattern that is characterized by a V
and M of 0.5 and 2, respectively:
• Enter the appropriate graph with these values, i.e., 0.5 and 2.
• The point of intersection shows that R(1–0.72 S
wi
) = 0.25.
• If the initial water saturation S
wi
is 0.21, solve for the recovery fac-
tor to give R = 0.29.
0.00
Permeability variation plotted against mobility
ratio, showing lines of constant E
R
(1 – S
w
) for a
producing WOR of 1.
0.0
0.1
0.2
0.3
0.4
0.5V
V
0.6
0.7
0.8
0.9
1.0
1.00
.40
.35
.30
.20
.15
.10
.05
R(1 – Sw) = .01
10.00 100
.25
M= –
k
rw
o
k
ro
k
ro
0.00
Permeability variation plotted against mobility
ratio, showing lines of constant E
R
(1 – 0.72 S
w
) for
a producing WOR of 5.
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.00
.45
.40
.35
.30
.25
.20
.15
.10
.05
R(1 – 0.72Sw) = .01
10.00 100
M= –
k
rw
o
w
0.00
Permeability variation plotted against mobility
ratio, showing lines of constant E
R
(1 – 0.40 S
w
) for
a producing WOR of 100.
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.00
.45
.40
.35
.30
.25
.20
.15
.10
.05
.01
R(1 – 0.40Sw) = .50
10.00 100
M= –
k
rw
o
w
0.00
Permeability variation plotted against mobility
ratio, showing lines of constant E
R
(1 – 0.52 S
w
) for
a producing WOR of 25.
0.0
0.1
0.2
0.3
0.4
0.5V
V
0.6
0.7
0.8
0.9
1.0
1.00
.50
.45
.40
.35
.30
.25
.20
.10
.05
.15
R(1–0.52 Sw)= .01
10.00 100
M= –
k
rw
o
w
k
ro
w
k
ro
Principles of Waterflooding 1007
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 1007
