Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.


Figure 15-1. Vapor pressures for hydrocarbon components. (Courtesy of the Gas
Processors Suppliers Association, Engineering Book, 10th Ed., 1987.)
1028 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1028

The vapor pressure chart allows a quick determination of p
v
of a
pure component at a specific temperature. For computer and spread-
sheet applications, however, an equation is more convenient. Lee and
Kesler (1975) proposed the following generalized vapor pressure
equation:
with
where p
v
= vapor pressure, psi
p
c
= critical pressure, psi
T
r
= reduced temperature (T / T
c
)
T = system temperature, °R
T
c
= critical temperature, °R
ω = acentric factor
EQUILIBRIUM RATIOS
In a multicomponent system, the equilibrium ratio K
i
of a given com-
ponent is defined as the ratio of the mole fraction of the component in the
gas phase y
i
to the mole fraction of the component in the liquid phase x
i
.
Mathematically, the relationship is expressed as:
where K
i
= equilibrium ratio of component i
y
i
= mole fraction of component i in the gas phase
x
i
= mole fraction of component i in the liquid phase
At pressures below 100 psia, Raoult’s and Dalton’s laws for ideal solu-
tions provide a simplified means of predicting equilibrium ratios. Raoult’s
law states that the partial pressure p
i
of a component in a multicomponent
K
y
x
i
i
i
=
(
)
15 -1
B
T
TT
r
rr
=−−
(
)
+
(
)
15 2518
15 6875
13 4721 0 4357
6
.
.
.ln .
A
T
TT
r
rr
=−−
(
)
+
(
)
5 92714
6 09648
1 2886 0 16934
6
.
.
.ln .
pp AB
vc
=+
(
)
exp ω
Vapor–Liquid Phase Equilibria 1029
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1029

system is the product of its mole fraction in the liquid phase x
i
and the
vapor pressure of the component p
vi
, or:
where p
i
= partial pressure of a component i, psia
p
vi
= vapor pressure of component i, psia
x
i
= mole fraction of component i in the liquid phase
Dalton’s law states that the partial pressure of a component is the product of
its mole fraction in the gas phase y
i
and the total pressure of the system p, or:
where p = total system pressure, psia.
At equilibrium and in accordance with the above stated laws, the par-
tial pressure exerted by a component in the gas phase must be equal to
the partial pressure exerted by the same component in the liquid phase.
Therefore, equating the equations describing the two laws yields:
Rearranging the above relationship and introducing the concept of the
equilibrium ratio gives:
Equation 15-4 shows that for ideal solutions and regardless of the overall
composition of the hydrocarbon mixture, the equilibrium ratio is only a
function of the system pressure p and the temperature T since the vapor
pressure of a component is only a function of temperature (see Figure 15-1).
It is appropriate at this stage to introduce and define the following
nomenclatures:
z
i
= mole fraction of component in the entire hydrocarbon mixture
n = total number of moles of the hydrocarbon mixture, lb-mol
n
L
= total number of moles in the liquid phase
n
v
= total number of moles in the vapor (gas) phase
By definition:
nn n
Lv
=+
(
)
15 - 5
y
x
p
p
K
i
i
vi
i
==
(
)
15 - 4
xp yp
ivi i
=
pyp
ii
=
(
)
15 - 3
pxp
iivi
=
(
)
15 - 2
1030 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1030

Equation 15-5 indicates that the total number of moles in the system is
equal to the total number of moles in the liquid phase plus the total num-
ber of moles in the vapor phase. A material balance on the i’th compo-
nent results in:
where z
i
n = total number of moles of component i in the system
x
i
n
L
= total number of moles of component i in the liquid
phase
y
i
n
v
= total number of moles of component i in the vapor
phase
Also by the definition of mole fraction, we may write:
It is convenient to perform all phase-equilibria calculations on the basis
of 1 mol of the hydrocarbon mixture, i.e., n = 1. That assumption reduces
Equations 15-5 and 15-6 to:
Combining Equations 15-4 and 15-11 to eliminate y
i
from Equation 15-11
gives:
Solving for x
i
yields:
x
z
nnK
i
i
Lvi
=
+
(
)
15 -12
xn xK n z
iL i i v i
+
(
)
=
xn yn z
iL iv i
+=
(
)
15 -11
nn
Lv
+=
(
)
115-10
y
i
i
=
(
)
∑
115-9
x
i
i
=
(
)
∑
115-8
z
i
i
=
(
)
∑
115-7
zn xn yn
iiLiv
=+
(
)
15 - 6
Vapor–Liquid Phase Equilibria 1031
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1031
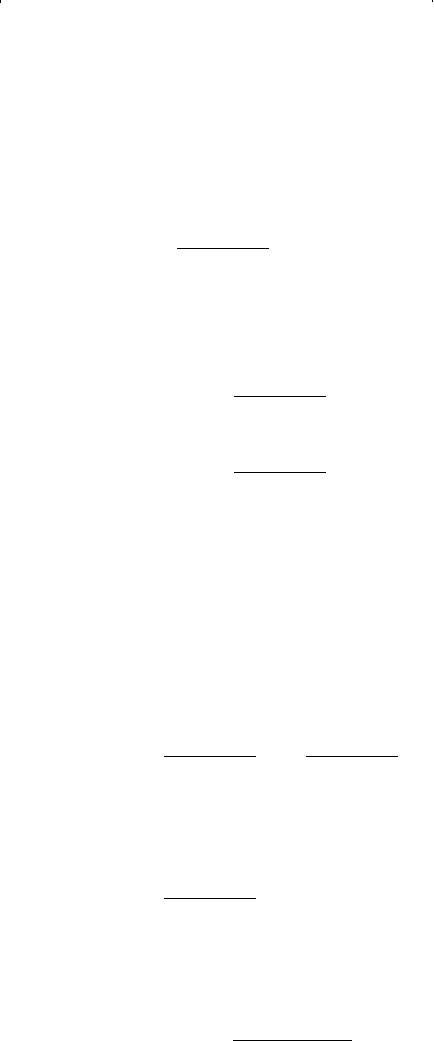
Equation 15-11 can also be solved for y
i
by combining it with Equa-
tion 15-4 to eliminate x
i
:
Combining Equation 15-12 with 15-8 and Equation 15-13 with 15-19
results in:
Since
Therefore,
or
Replacing n
L
with (1 – n
v
) yields:
The above set of equations provides the necessary phase relationships to
perform volumetric and compositional calculations on a hydrocarbon
system. These calculations are referred to as flash calculations and are
discussed next.
fn
zK
nK
v
ii
vi
i
(
)
=
−
(
)
−
(
)
+
=
(
)
∑
1
11
015-16
zK
nnK
ii
Lvi
i
−
(
)
+
=
∑
1
0
zK
nnK
z
nnK
ii
Lvi
i
i
Lvi
i
+
−
+
=
∑∑
0
yx
ii
ii
−=
∑∑
0
y
zK
nnK
i
ii
Lvi
ii
=
+
=
(
)
∑∑
115-15
x
z
nnK
i
i
Lvi
ii
=
+
=
(
)
∑∑
115-14
y
zK
nnK
xK
i
ii
Lvi
ii
=
+
=
(
)
15 -13
1032 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1032

FLASH CALCULATIONS
Flash calculations are an integral part of all reservoir and process engi-
neering calculations. They are required whenever it is desirable to know
the amounts (in moles) of hydrocarbon liquid and gas coexisting in a
reservoir or a vessel at a given pressure and temperature. These calcula-
tions are also performed to determine the composition of the existing
hydrocarbon phases.
Given the overall composition of a hydrocarbon system at a speci-
fied pressure and temperature, flash calculations are performed to
determine:
• Moles of the gas phase n
v
• Moles of the liquid phase n
L
• Composition of the liquid phase x
i
• Composition of the gas phase y
i
The computational steps for determining n
L
, n
v
, y
i
, and x
i
of a hydro-
carbon mixture with a known overall composition of z
i
and character-
ized by a set of equilibrium ratios K
i
are summarized in the following
steps:
Step 1. Calculation of n
v
: Equation 15-16 can be solved for n
v
by using
the Newton–Raphson iteration techniques. In applying this itera-
tive technique:
• Assume any arbitrary value of n
v
between 0 and 1, e.g., n
v
= 0.5.
A good assumed value may be calculated from the following rela-
tionship, providing that the values of the equilibrium ratios are
accurate:
where
• Evaluate the function f(n
v
) as given by Equation 15-16 using
the assumed value of n
v
.
BzKK
ii i
i
=−
(
)
[]
∑
1
AzK
ii
i
=−
(
)
[]
∑
1
nAAB
v
=−
(
)
Vapor–Liquid Phase Equilibria 1033
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1033
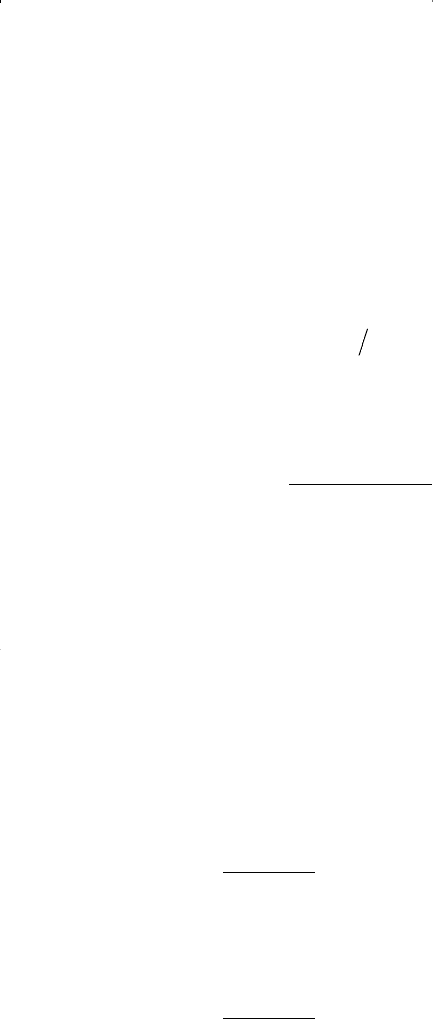
• If the absolute value of the function f(n
v
) is smaller than a pre-
set tolerance, e.g., 10
–15
, then the assumed value of n
v
is the
desired solution.
• If the absolute value of f(n
v
) is greater than the preset toler-
ance, then a new value of n
v
is calculated from the following
expression:
with
where (n
v
)
n
is the new value of n
v
to be used for the next
iteration.
• The above procedure is repeated with the new values of n
v
until convergence is achieved.
Step 2. Calculation of n
L
: Calculate the number of moles of the liquid
phase from Equation 15-10, to give:
Step 3. Calculation of x
i
: Calculate the composition of the liquid phase
by applying Equation 15-12:
Step 4. Calculation of y
i
: Determine the composition of the gas phase
from Equation 15-13:
Example 15-1
A hydrocarbon mixture with the following overall composition is
flashed in a separator at 50 psia and 100°F.
y
zK
nnK
xK
i
ii
Lvi
ii
=
+
=
x
z
nnK
i
i
Lvi
=
+
nn
Lv
=−1
′
=−
−
(
)
−
(
)
+
[]
∑
f
zK
nK
ii
vi
i
1
11
2
2
nnnfn
v
n
vv v
(
)
=−
(
)
′
(
)
f
1034 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1034
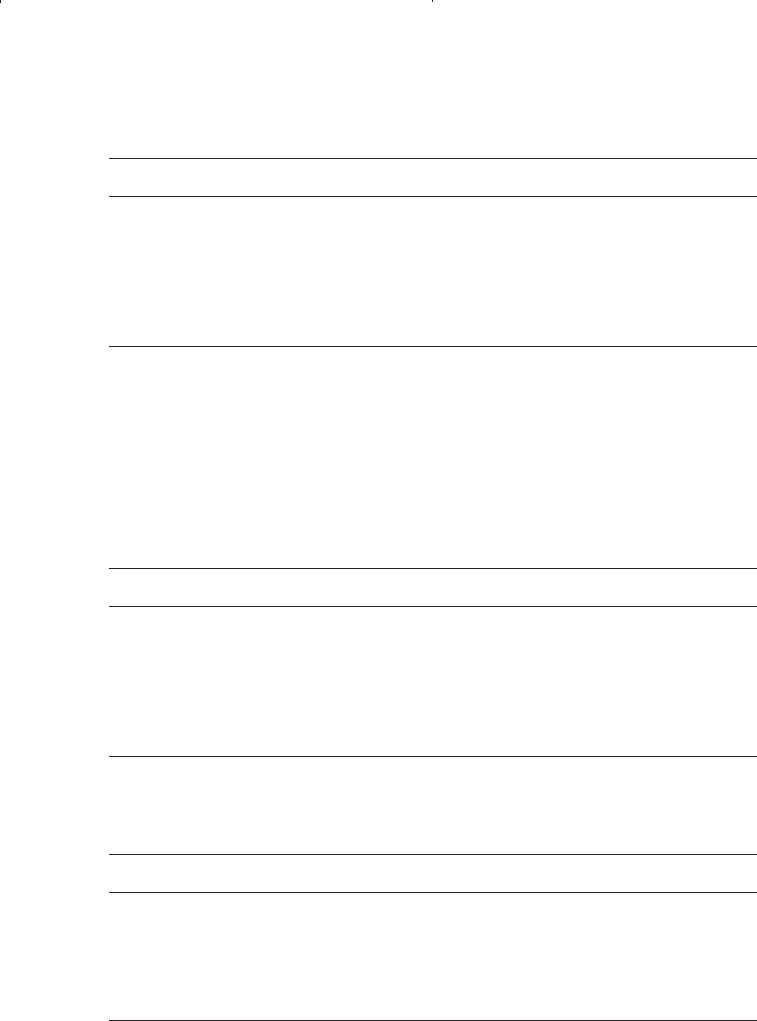
Component z
i
C
3
0.20
i – C
4
0.10
n – C
4
0.10
i – C
5
0.20
n – C
5
0.20
C
6
0.20
Assuming an ideal solution behavior, perform flash calculations.
Solution
Step 1. Determine the vapor pressure for the Cox chart (Figure 15-1) and
calculate the equilibrium ratios from Equation 15-4.
Component z
i
p
vi
at 100°F K
i
= p
vi
/50
C
3
0.20 190 3.80
i – C
4
0.10 72.2 1.444
n – C
4
0.10 51.6 1.032
i – C
5
0.20 20.44 0.4088
n – C
5
0.20 15.57 0.3114
C
6
0.20 4.956 0.09912
Step 2. Solve Equation 15-16 for n
v
by using the Newton–Raphson
method, to give:
Iteration n
v
f(n
v
)
0 0.08196579 3.073 E-02
1 0.1079687 8.894 E-04
2 0.1086363 7.60 E-07
3 0.1086368 1.49 E-08
4 0.1086368 0.0
Step 3. Solve for n
L
:
n
L
=− =1 0 1086368 0 8913631..
nn
Lv
=−1
Vapor–Liquid Phase Equilibria 1035
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1035

Step 4. Solve for x
i
and y
i
to yield:
Component z
i
K
i
y
i
= x
i
K
i
C
3
0.20 3.80 0.1534 0.5829
i – C
4
0.10 1.444 0.0954 0.1378
n – C
4
0.10 1.032 0.0997 0.1029
i – C
5
0.20 0.4088 0.2137 0.0874
n – C
5
0.20 0.3114 0.2162 0.0673
C
6
0.20 0.09912 0.2216 0.0220
Notice that for a binary system, i.e., two-component system, flash calcu-
lations can be performed without restoring to the above iterative tech-
nique by applying the following steps:
Step 1. Solve for the composition of the liquid phase x
i
. From equa-
tions 15-8 and 15-9:
Solving the above two expressions for the liquid compositions x
1
and x
2
gives:
and
where x
1
= mole fraction of the first component in the liquid
phase
x
2
= mole fraction of the second component in the liquid
phase
K
1
= equilibrium ratio of the first component
K
2
= equilibrium ratio of the second component
xx
21
1=−
x
K
KK
1
2
12
1
=
−
−
yyy KxKx
i
i
=+= + =
∑
12 11 22
1
xxx
i
i
=+=
∑
12
1
xz K
ii i
=+0 8914 0 1086..
(())
1036 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1036

Step 2. Solve for the composition of the gas phase y
i
. From the defini-
tion of the equilibrium ratio, calculate the composition of the gas
as follows:
Step 3. Solve for the number of moles of the vapor phase n
v
. Arrange
Equation 15-12 to solve for n
v
, to give:
and
where z
1
= mole fraction of the first component in the entire
system
x
1
= mole fraction of the first component in the liquid
phase
K
1
= equilibrium ratio of the first component
K
2
= equilibrium ratio of the second component
EQUILIBRIUM RATIOS FOR REAL SOLUTIONS
The equilibrium ratios, which indicate the partitioning of each compo-
nent between the liquid phase and gas phase, as calculated by Equation
15-4 in terms of vapor pressure and system pressure, proved to be inade-
quate. The basic assumptions behind Equation 15-4 are that:
• The vapor phase is an ideal gas as described by Dalton’s law
• The liquid phase is an ideal solution as described by Raoult’s law
The above combination of assumptions is unrealistic and results in inac-
curate predictions of equilibrium ratios at high pressures.
nn
v1
1=−
n
zx
xK
v
=
−
−
(
)
11
11
1
yxK y
222 1
1==−
yxK
111
=
Vapor–Liquid Phase Equilibria 1037
Reservoir Eng Hndbk Ch 15 2001-10-25 17:41 Page 1037
