Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.


Dake used the above two parameters to define the following stability criteria:
• If M* > 1. The displacement is stable if G > (M* – 1), in which case the
fluid interface angle < . The displacement is unstable if G < (M* – 1).
• If M* = 1. This is a very favorable condition, because there is no ten-
dency for the water to bypass the oil. The displacement is considered
unconditionally stable and is characterized by the fact that the interface
rises horizontally in the reservoir, i.e., = .
• If M* < 1. When the end-point mobility ratio M* is less than unity, the
displacement is characterized as unconditionally stable displacement
with B > (Figure 14-48b).
The author also defined the critical flow rate, i
crit
by:
where i
crit
= critical water injection rate, bbl/day
k
rw
= relative permeability to water @ S
or
w
= water viscosity, cp
k = absolute permeability, md
= dip angle
Example 14-17
A tilted linear reservoir is under consideration for waterflooding. The
rock and fluid properties are given below:
Cross-sectional area A = 31,250 ft
2
Absolute permeability k = 70 md
Dip angle = 20°
Water density
w
= 63 lb/ft
3
Oil density
o
= 35 lb/ft
3
Water viscosity
w
= 0.5 cp
Oil viscosity
o
= 3.0 cp
k
rw
@ S
or
= 0.35
k
ro
@ S
wi
= 1.00
Water-injection rate = 800 bbl/day
Calculate the critical water injection rate for water displacing oil updip.
i
kk A
M
crit
rw w o
w
=
×−
(
)
(
)
−
(
)
(
)
−
7 853 10
1
6
. sin
*
ρρ α
µ
14 - 89
988 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 988

Solution
Step 1. Calculate the end-point mobility ratio from Equation 14-88:
Step 2. Calculate the critical injection rate by using Equation 14-89:
The above example indicates that the water injection rate must be 106
bbl/day to ensure a stable displacement, which, when compared with the
proposed injection rate of 800 bbl/day, is perhaps not economically feasi-
ble to maintain.
Dake (1978) and Willhite (1986) presented a comprehensive treatment
of water displacement under segregated flow conditions.
III. VERTICAL SWEEP EFFICIENCY
The vertical sweep efficiency, E
V
, is defined as the fraction of the ver-
tical section of the pay zone that is the injection fluid. This particular
sweep efficiency depends primarily on (1) the mobility ratio and (2) total
volume injected. As a consequence of the nonuniform permeabilities, any
injected fluid will tend to move through the reservoir with an irregular
front. In the more permeable portions, the injected water will travel more
rapidly than in the less permeable zone.
Perhaps the area of the greatest uncertainty in designing a waterflood
is the quantitative knowledge of the permeability variation within the
reservoir. The degree of permeability variation is considered by far the
most significant parameter influencing the vertical sweep efficiency.
To calculate the vertical sweep efficiency, the engineer must be able to
address the following three problems:
1. How to describe and define the permeability variation in mathematical
terms
2. How to determine the minimum number of layers that are sufficient to
model the performance of the fluid
3. How to assign the proper average rock properties for each layer (called
the zonation problem)
i bbl day
crit
=
×−
−
=
−
(
)
(
)
(
)
(
)
(
)
(
)
7 853 10 70 0 35 31 250 63 35 20
0521 1
106
6
. . , sin
..
/
M*
.
.
.
.
.==
035
100
30
05
20
Principles of Waterflooding 989
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 989

A complete discussion of the above three problems is given below.
Reservoir Vertical Heterogeneity
As pointed out in Chapter 4, one of the first problems encountered by
the reservoir engineer is that of organizing and utilizing the large amount
of data available from core and well logging analyses. Although porosity
and connate water saturation may vary aerially and vertically within a
reservoir, the most important rock property variation to influence water-
flood performance is permeability. Permeabilities pose particular prob-
lems because they usually vary by more than an order of magnitude
between different strata.
Dykstra and Parsons (1950) introduced the concept of the permeability
variation V, which is designed to describe the degree of heterogeneity
within the reservoir. The value of this uniformity coefficient ranges
between zero for a completely homogeneous system and one for a com-
pletely heterogeneous system. Example 4-18 of Chapter 4 illustrates the
required computational steps for determining the coefficient V that is
given by Equation 4-70, as:
To further illustrate the use of the Dykstra and Parsons permeability vari-
ation, Craig (1971) proposed a hypothetical reservoir that consists of 10
wells (wells A through J) with detailed permeability data given for each
well, as shown in Table 14-2. Each well is characterized by 10 values of
permeability with each value representing 1 ft of pay.
Arranging all of these permeability values, i.e., the entire 100 perme-
ability values, from maximum to minimum, Craig (1971) obtained the
permeability distribution as shown in the log-probability scale of Figure
14-49. The resulting permeability distribution indicates that this hypo-
thetical reservoir is characterized by a permeability variation of 70%, or:
V
kk
k
=
−
=
−
=
50
84 1
50
10 3
10
07
.
.
V
kk
k
=
−
50
84 1
50
.
990 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 990
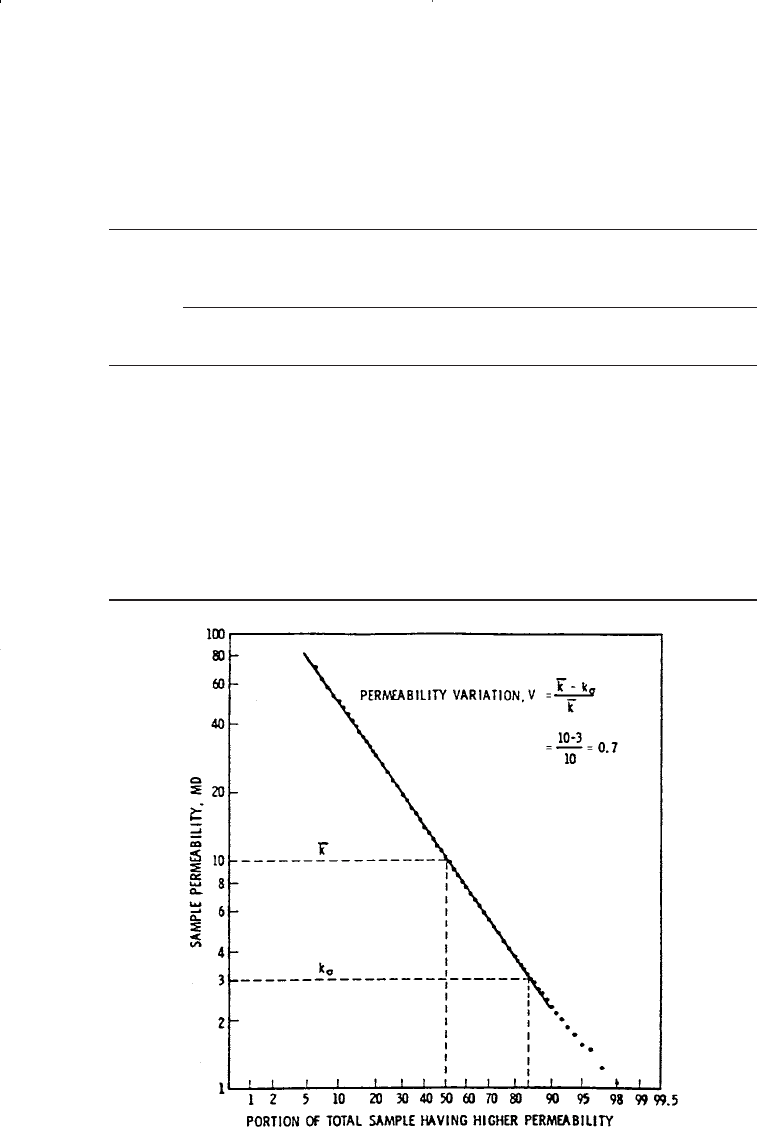
Table 14-2
Ten-Layer Hypothetical Reservoir
(Permission to publish by the Society of Petroleum Engineers)
CORE ANALYSIS FOR HYPOTHETICAL RESERVOIR
Cores from 10 Wells, A Through J; Each Permeability Value (md)
Represents 1 ft of Pay
Depth
(ft) A B C D E F G H I J
6791 2.9 7.4 30.4 3.8 8.6 14.5 39.9 2.3 12.0 29.0
6792 11.3 1.7 17.6 24.6 5.5 5.3 4.8 3.0 0.6 99.0
6793 2.1 21.2 4.4 2.4 5.0 1.0 3.9 8.4 8.9 7.6
6794 167.0 1.2 2.6 22.0 11.7 6.7 74.0 25.5 1.5 5.9
6795 3.6 920.0 37.0 10.4 16.5 11.0 120.0 4.1 3.5 33.5
6796 19.5 26.6 7.8 32.0 10.7 10.0 19.0 12.4 3.3 6.5
6797 6.9 3.2 13.1 41.8 9.4 12.9 55.2 2.0 5.2 2.7
6798 50.4 35.2 0.8 18.4 20.1 27.8 22.7 47.4 4.3 66.0
6799 16.0 71.5 1.8 14.0 84.0 15.0 6.0 6.3 44.5 5.7
6800 23.5 13.5 1.5 17.0 9.8 8.1 15.4 4.6 9.1 60.0
Figure 14-49. Determination of permeability variation for the hypothetical reser-
voir. (Permission to publish by the Society of Petroleum Engineers.)
Principles of Waterflooding 991
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 991

Minimum Number of Layers
Based on a computer study, Craig (1971) outlined some guidelines for
selecting the minimum number of layers needed to predict the perfor-
mance of a reservoir under waterflooding operation. The author simulated
the performance of a waterflood five-spot pattern that is composed of 100
layers with permeability variations ranging from 0.4 to 0.8. The minimum
number of layers required to match results of the 100-layer model was
determined as a function of mobility ratio M and permeability variation V.
Tables 14-3 through 14-5 summarize results of these simulations and pro-
vide a guide to selection of the number of layers for five-spot patterns.
Table 14-3
Minimum Number of Layers for WOR > 2.5
(Permission to publish by the Society of Petroleum Engineers)
Permeability Variation
Mobility
Ratio 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.05 112410202020
0.111241020100100
0.211241020100100
0.512241020100100
1.013341020100100
2.0 2 4 4 10 20 50 100 100
5.0 2 5 10 20 50 100 100 100
Table 14-4
Minimum Number of Layers for WOR > 5
(Permission to publish by the Society of Petroleum Engineers)
Permeability Variation
Mobility
Ratio 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.05 11245101020
0.11124101010100
0.21124101020100
0.51224101020100
1.01234101020100
2.02345101050100
5.0 2 4 5 10 20 100 100 100
992 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 992

Table 14-5
Minimum Number of Layers for WOR > 10
(Permission to publish by the Society of Petroleum Engineers)
Permeability Variation
Mobility
Ratio 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.05 1112451020
0.11112551020
0.21123551020
0.51123551020
1.011235101050
2.01234101020100
5.0134510100100100
Example 14-18
A reservoir is under consideration for waterflooding. The heterogene-
ity of the reservoir is described by a permeability variation V of 40%.
The mobility ratio is determined as 2.0. Determine the minimum number
of layers required to perform waterflooding calculations.
Solution
Table 14-4 shows that the minimum number of layers required to
match the performance of the 100-layer computer model with a produc-
ing WOR above 10 STB/STB is 4 layers.
The Zonation Problem
In waterflooding calculations, it is frequently desirable to divide the
reservoir into a number of layers that have equal thickness but different
permeabilities and porosities. Traditionally, two methods are used in the
industry to assign the proper average permeability for each layer: (1) the
positional method or (2) the permeability ordering method.
Positional Method
The positional method describes layers according to their relative
location within the vertical rock column. This method assumes that the
Principles of Waterflooding 993
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 993

injected fluid remains in the same elevation (layer) as it moves from
the injector to the producer. Miller and Lents (1966) successfully
demonstrated this concept in predicting the performance of the Bod-
caw Reservoir Cycling Project. The authors proposed that the average
permeability in a selected layer (elevation) should be calculated by
applying the geometric-average permeability as given by Equation
4-54 or 4-55:
If all the thicknesses are equal, then:
Example 14-19
Using the core analysis data given in Table 14-2 for the 10-well sys-
tem, assign the proper average permeability for each layer if the reservoir
is divided into:
a. 10 equal-thickness layers, each with a 1-ft thickness
b. 5 equal-thickness layers, each with a 2-ft thickness
Solution
a. Using the positional method approach and applying Equation 4-55,
calculate the permeability for each 1-ft layer:
A similar approach for calculating the permeability for the remaining
layers yields:
Layer 1= 10 md29 74 304 38 86 145 399 23 120 290
110
.. ... . .. . .
/
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
[]
=
kkkkk
avg n
n
=
(
)
123
1
K
/
k
hk
h
avg
ii
i
n
i
i
n
=
(
)
=
=
∑
∑
exp
ln
1
1
994 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 994

Layer # Permeability, md
1 10.0
2 6.8
3 4.7
4 10.4
5 20.5
6 12.1
7 8.6
8 18.4
9 14.3
10 10.9
b. Five equal-thickness layers:
Step 1. Calculate the arithmetic-average permeability for each layer per
location:
Depth A B C D E F G H I J
6791–92 7.10 4.55 24.00 14.20 7.05 9.90 22.35 2.65 6.30 64.00
93–94 84.55 11.20 3.50 12.20 8.35 3.85 38.95 16.95 5.20 6.75
95–96 11.55 473.30 22.40 21.20 13.60 10.50 69.50 8.25 3.40 20.00
97–98 28.65 19.20 6.95 30.10 14.75 20.35 38.95 24.70 4.75 34.35
99–00 19.75 42.50 1.65 15.50 46.90 13.05 10.70 5.45 26.80 32.85
Step 2. Use the geometric-average method to calculate the permeability
in each layer:
Remaining layers are treated in the same fashion to give:
Layer # Permeability, md
1 10.63
2 11.16
3 20.70
4 18.77
5 15.26
Layer 1==
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
[]
71 45 240 142 705 99 2235 265 63 640 1063
110
.......... .
/
Principles of Waterflooding 995
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 995

Permeability Ordering Method
The permeability ordering method is essentially based on the Dykstra
and Parsons (1950) permeability sequencing technique. The core analy-
sis permeabilities are arranged in a decreasing permeability order and a
plot like that shown in Figure 14-49 is made. The probability scale is
divided into equal-percent increments with each increment representing a
layer. The permeability for each layer is assigned to the permeability
value that corresponds to the midpoint of each interval.
Example 14-20
For the 10-layer system of Example 14-19, determine the permeability
for each layer by using the permeability ordering approach.
Solution
From Figure 14-49, determine the permeability for each of the 10 lay-
ers by reading the permeability at the following midpoints: 5, 15, 25, 35,
45, 55, 65, 75, 85, and 95%:
Layer #1 Permeability Ordering Positional Approach
1 84.0 10.0
2 37.0 6.8
3 23.5 4.7
4 16.5 10.4
5 12.0 20.5
6 8.9 12.1
7 6.5 8.6
8 4.6 18.4
9 3.0 14.3
10 1.5 10.9
Porosity assignments for the selected reservoir layers may also be treated
in a similar manner to that of the permeability ordering approach. All
porosity measurements are arranged in decreasing order and a plot of the
porosity versus percentage of thickness with greater porosity is made on a
Cartesian-probability scale (rather than a log-probability scale). The porosi-
ty of each layer can then be obtained for each interval of thickness selected.
The permeability ordering technique is perhaps the most widely used
approach in the petroleum industry when determining the vertical sweep
efficiency.
996 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 996
Calculation of Vertical Sweep Efficiency
Basically two methods are traditionally used in calculating the vertical
sweep efficiency EV: (1) Stiles’ method and (2) the Dykstra–Parsons
method. These two methods assume that the reservoir is composed of an
idealized layered system, as shown schematically in Figure 14-50. The
layered system is selected based on the permeability ordering approach
with layers arranged in order of descending permeability. The common
assumptions of both methods are:
• No cross-flow between layers
• Immiscible displacement
• Linear flow
• The distance water has traveled through each layer is proportional to
the permeability of the layer
• Piston-like displacement
Figure 14-50. Idealized layered system.
Overall Recovery
Time
Primary
Secondary
Tertiary
Field Flow Rate
Time
Primary
Secondary
Tertiary
Principles of Waterflooding 997
Reservoir Eng Hndbk Ch 14 2001-10-25 17:38 Page 997
