Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

Properties of the DFT

sequence x{n + m) can be obtained by rotating the circle in Fig. 4.1 in the

clockwise direction by m positions. If there are N values in a sequence,

then only N

—

1 unique shifts are possible. x(n

—

m) is the signal delayed

by m sample intervals and x(n + m) is the signal advanced by m sample

intervals. Substituting n

—

m for n in the IDFT definition, we get

x(n -m) = 1 £

X(k)W^

m)k

= 1

X)(W3?*A:(*))W^,

*=0 fc=0

as both x(n) and Wj^"* are periodic functions, where n =

0,1,...,

—

x(n

m) &

W£

X(k)

In shifting a waveform, obviously, its form and amplitude remain unchanged.

Therefore, the shift results only in a change of the phase shift in the

frequency-domain representation. The multiplication by the complex ex-

ponential in the frequency-domain is just changing the phase. The delay

(advance) of the signal x{n) by m samples produces a phase shift of—j^mk

(jij-mk) radians. Figure 4.2 shows the DFT of x(n

—

1) in terms of X(k)

multiplied by appropriate complex exponential.

Example 4.3 Consider the DFT pair

z(n) = {0,1,1,0}^X(fc) =

{2,-1-j,

0,-1+j}

Now,

s(n-l) = {0,0,l,l} &

W*X(k)

(-j)

X(k)

= {2,-l +

j,0,-l-j}

ar(n + l) = {l,l,0,0} <*

X(k)

= (j)

X(k) = {2,1-j,0,l+j} 1

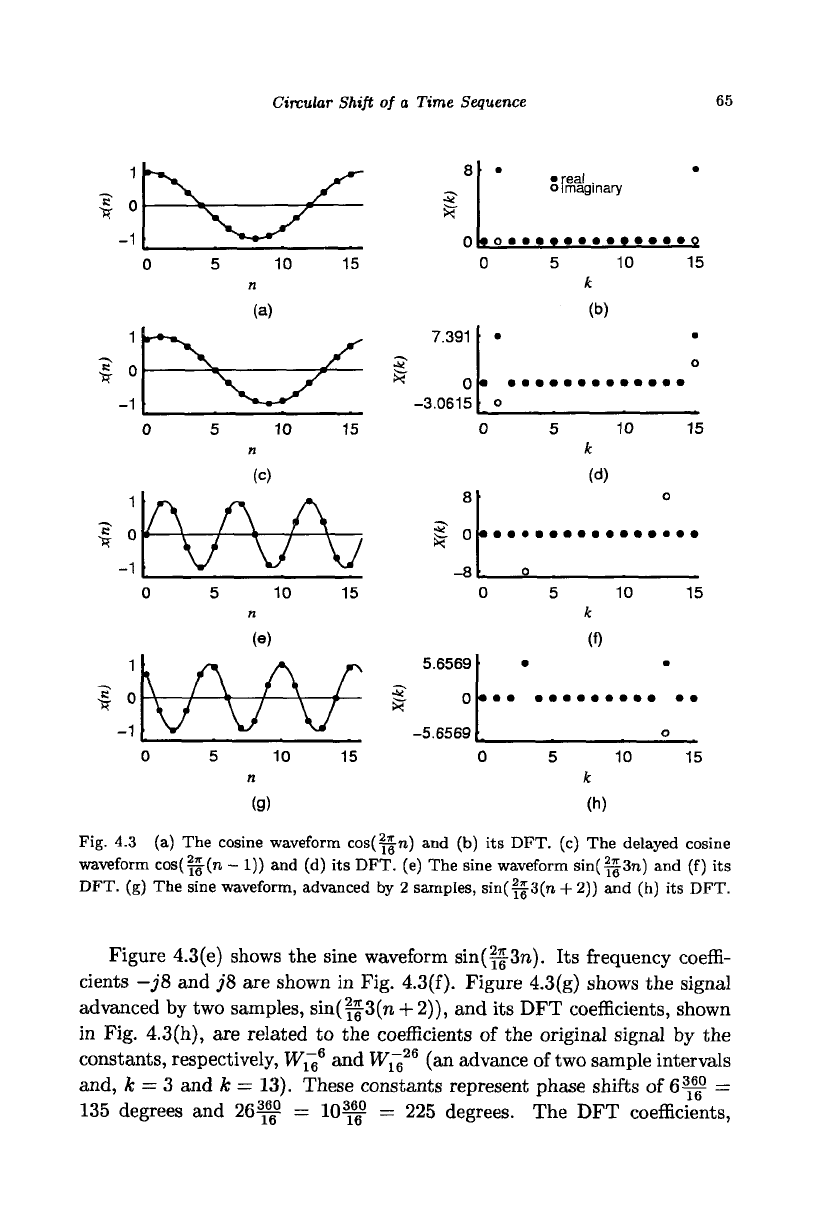
Example 4.4 Figure 4.3(a) shows one cycle of the cosine waveform

cos(^-n).

Its frequency coefficients 8 and 8 are shown in Fig. 4.3(b). Fig-

ure 4.3(c) shows the signal delayed by one sample, cos(f|(n

—

1)), and

its DFT coefficients, shown in Fig. 4.3(d), are related to the coefficients

of the original signal by the constants, respectively, Wl

and W^ (a de-

lay of one sample interval and, k = 1 and k = 15). These constants

represent phase delays of -1^ = -22.5 degrees and -15^ = -337.5

degrees, respectively. The DFT coefficients, shown in Fig. 4.3(d), of the

shifted signal are 8^ = 8cos(-22.5) + j8sin(-22.5) = 7.391 - j'3.0615

and 8W$ = 8cos(-337.5) + j8sin(-337.5) = 7.391 + J3.0615.

Circular Shift of a Time Sequence

• real .

o imaginary

10 15

(a)

5 10

(b)

£ °

-1

* °

-1

I ^

-1

v /

I \

1 \

(c)

A /*

\ *

(e)

J \

\S \

(g)

7.391

-3.0615

•

-8

5.6569

-5.6569

•

(d)

(f)

(h)

•

Fig. 4.3 (a) The cosine waveform cos(^|-n) and (b) its DFT. (c) The delayed cosine

waveform cos(|^(n - 1)) and (d) its DFT. (e) The sine waveform sin(||3n) and (f) its

DFT. (g) The sine waveform, advanced by 2 samples, sin(||-3(n + 2)) and (h) its DFT.

Figure 4.3(e) shows the sine waveform sin(^3n). Its frequency coeffi-

cients —j8 and j8 are shown in Fig. 4.3(f). Figure 4.3(g) shows the signal

advanced by two samples, sin(||3(n + 2)), and its DFT coefficients, shown

in Fig. 4.3(h), are related to the coefficients of the original signal by the

constants, respectively,

W{~

and W^?

(an advance of two sample intervals

and, k = 3 and k — 13). These constants represent phase shifts of 6^ =

135 degrees and 26^ = 10^f = 225 degrees. The DFT coefficients,

66 Properties

the

DFT

Table 4.1 Computing

the

4-point DFTs

overlapping segments

of a

sequence,

x(n).

x(n) 2

X(k) lO

j'13

X(k)

1+J4

-3+jO

+ jl8

X(k)

2-j5

-5+jO

I8+7I8

X(k)

3+j5

-1-J4

-5

0+jO

+ jl8

5+j6

1-J2

0+jO

+ J4

-2

- j6

+ J3

-6

+ j2

shown

in Fig.

4.3(h),

of the

shifted signal

are -j8W

-j'8cos(135)

j(-j8)sin(135)

5.657+j5.657andj8W^

j8cos(225)+j(j'8)sin(225)

5.657

J5.657.

DFT

overlapping segments

of a

sequence

the

iV-point DFTs

overlapping segments

of a

sequence

are

required,

the first iV-point

DFT can be

computed using

fast

DFT

algorithm

and the

rest

can be

computed

much less computational cost. With

overlap

N - 1

samples,

the

set of

data

different from

the

current

set

in that

the

first value

lost

and a new

value

added

at the end. Let

the

DFT of

x(n),n

0,1,..

.,N - 1 be X(k). The DFT of

x(n),n

N, 1,2,..., N - 1 is X(k) + x(N) - x(0). If we

circularly left shift

the

data

by one

sample interval,

we get

x(n),n

= 1,2,...,

iV.

The DFT of

this

sequence

is (X(k) + x(N) -

^(O))^*,

k =

0,1,..., JV

- 1.

Consider

the

sequence

x(n)

shown

in the

first

row of

Table

4.1.

The DFT of

the first four

values

computed directly.

The DFT of

adjacent

set of 4

input values

can

be computed using

the

formula given above. Table

4.1

shows

the DFT of

four adjacent sets. Note that

the

computational complexity

computing

the

DFT of

each

set

except

the

first

only

0(N).

4.4 Circular Shift

of a

Spectrum

The converse

the previous theorem

that

if a

time-domain signal

mul-

tiplied

by a

complex exponential

to get a

new time-domain signal W^

x(n),

then

the

spectrum

of the new

signal

that

of the

original signal circularly

shifted

by m

positions.

W±

x{n)&X(k±m)

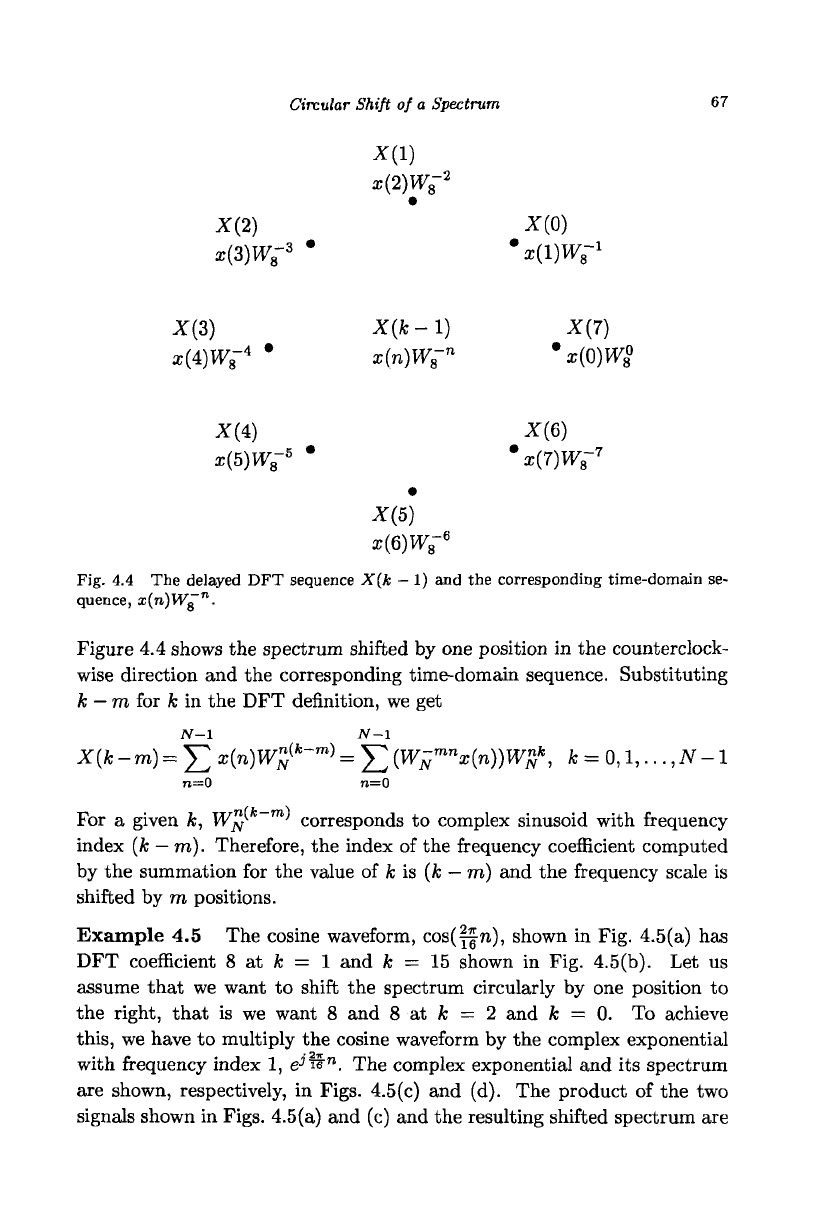
Circular Shift of a Spectrum

X(l)

X(2)

x(3)Wi

*(3)

x(4)W

X(4)

x(5)W

x(2)W

•

X(fc - 1)

x(n)W

X(5)

x(6)Wf

X(0)

X{7)

*x(0)Wi

X(6)

'x(7)W

Fig. 4.4 The delayed DFT sequence X(k

—

1) and the corresponding time-domain se-

quence, x(ra)Vl^~

Figure 4.4 shows the spectrum shifted by one position in the counterclock-

wise direction and the corresponding time-domain sequence. Substituting

—

m for k in the DFT definition, we get

JV-l N-l

^(fc-m)^^^)^-"

^^^^"^))^, k =

0,l,...,N-l

n=0 n=0

For a given k, W^ ~

' corresponds to complex sinusoid with frequency

index {k

—

m). Therefore, the index of the frequency coefficient computed

by the summation for the value of k is (k

—

m) and the frequency scale is

shifted by m positions.

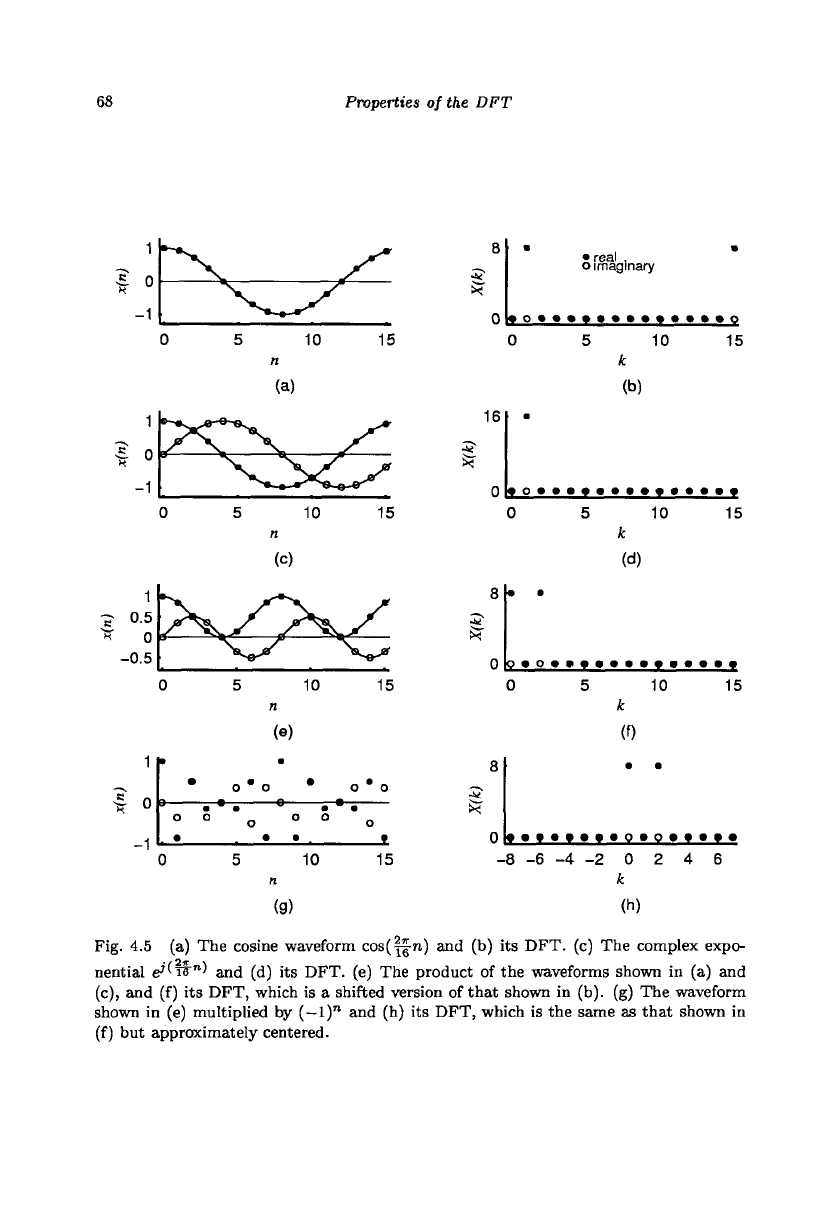
Example 4.5 The cosine waveform, cos(y|n), shown in Fig. 4.5(a) has

DFT coefficient 8 at k = 1 and k = 15 shown in Fig. 4.5(b). Let us

assume that we want to shift the spectrum circularly by one position to

the right, that is we want 8 and 8 at k = 2 and k = 0. To achieve

this,

we have to multiply the cosine waveform by the complex exponential

with frequency index 1,

w".

The complex exponential and its spectrum

are shown, respectively, in Figs. 4.5(c) and (d). The product of the two

signals shown in Figs. 4.5(a) and (c) and the resulting shifted spectrum are

Properties of the DFT

Ow o '

• real .

o imaginary

-1

(a)

(c)

5 10 15

(g)

0HL2J

8 •

0 bto

(b)

(d)

10 15

(f)

0 w»*»»»»»o»o»»»»«

-8-6-4-2 0 2 4 6

(h)

Fig. 4.5 (a) The cosine waveform cos(||-n) and (b) its DFT. (c) The complex expo-

nential

e*'ff"'

and (d) its DFT. (e) The product of the waveforms shown in (a) and

(c),

and (f) its DFT, which is a shifted version of that shown in (b). (g) The waveform

shown in (e) multiplied by ( —

1)"

and (h) its DFT, which is the same as that shown in

(f) but approximately centered.

Time-Reversal Property

shown, respectively, in Figs. 4.5(e) and (f). We can specify the spectrum

from looking at Fig. 4.5(e). The waveform corresponding to the real part

consists of a dc and a cosine wave with frequency index two, each with an

amplitude of 0.5. The imaginary part is a sine waveform with frequency

index two and amplitude 0.5. These waveforms produce a spectral value of

8 at frequency indices 0 and two, which is a shifted version of the spectrum

shown in Fig. 4.5(b).

A particular case, which is often used in practice, is the multiplication

of the input signal with W^ = (-1)", with N even. Figure 4.5(g) shows

the signal that is the product of the signal in Fig. 4.5(e) and (-1)"- Fig-

ure 4.5(h) shows its spectrum which is the same as that of Fig. 4.5(f) with

a shift of ~ = 8 sample intervals. Since we are multiplying the given signal

by a complex sinusoid with frequency index ^» the spectrum is shifted by

half the number of sample intervals (^) so that the origin is at about the

center (center-zero format). Note that neither the magnitude nor the phase

of the DFT coefficients changes. Only the position of the coefficients on

the frequency scale changes. I

4.5 Time-Reversal Property

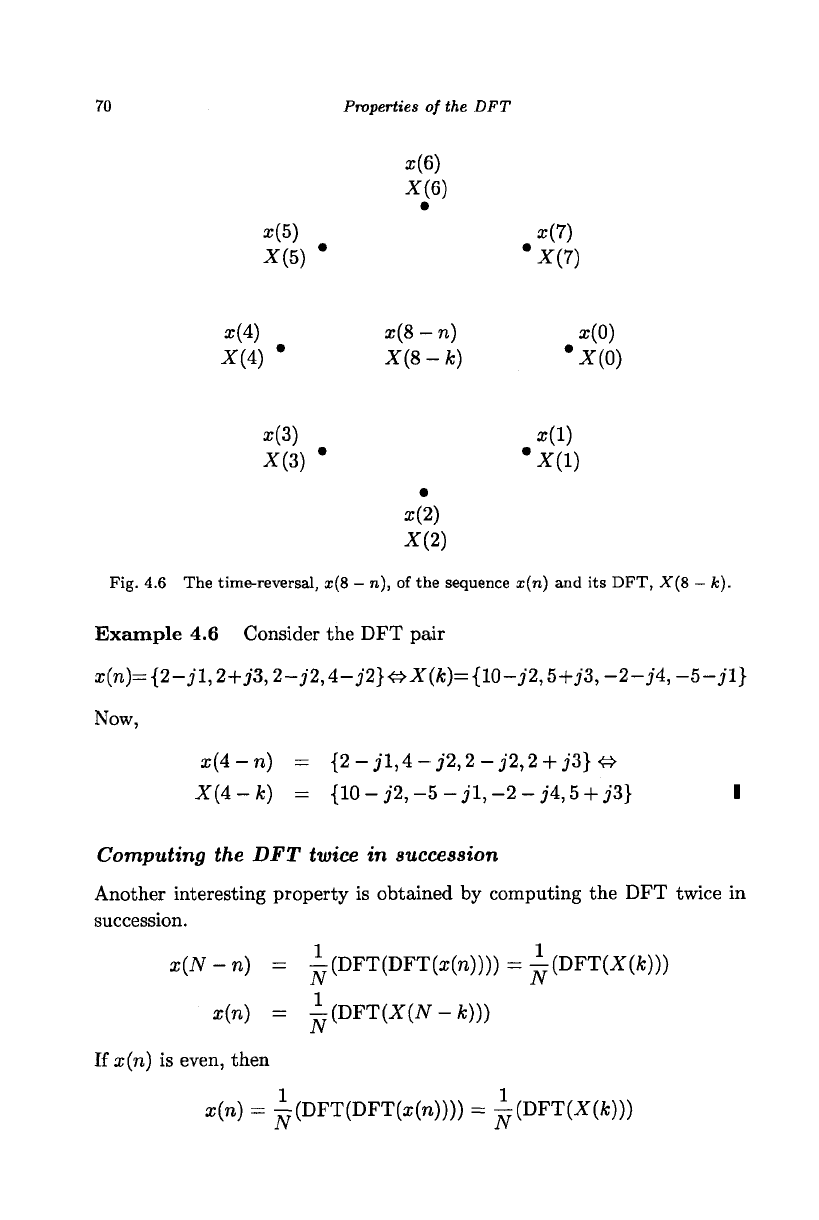
The time reversal of the sequence x(n) = {ar(0),x(l),x(2),a;(3),a;(4),a;(5),

x(6),x(7)} is x(&-n) = {x(0),x(7),x(6),x(5),x(4),x(3),x{2),x(l)} shown

in Fig. 4.6, which is the placing of the values of the sequence in a clockwise

direction starting from x(0). The DFT of a reversed sequence is the reversal

of the DFT coefficients of the original sequence as shown in Fig. 4.6. If

x(n) & X(k), then x(N - n) <=> X(N

—

k). By changing the frequency

index k to N

—

k in Eq. (3.6), we get

X(N - k) = £ x(n)W$

-V = £ *(n)W-»\ k =

0,1,...,

N - 1

n=0 n=0

The sum of the products a;(n)W

_nfc

is, obviously, equal to the sum of the

products x(N -

n)W

That is,

JV-l

X{N-h)=^x{N- n)W£

n=0

Properties of the DFT

x(5)

X(5) *

x(4)

X(4) *

x(3)

X{3) *

x(6)

X(6)

•

x(8 - n)

X(8 - k)

x(2)

X(2)

x(7)

*X(7)

x(0)

•X(0)

x(l)

*X(1)

Fig. 4.6 The time-reversal, x(8 - n), of the sequence x(n) and its DFT, X(8 - k).

Example 4.6 Consider the DFT pair

x{n)= {2-jl, 2+j3,2-j2,4-j2}&X(k)= {10-j2,5+J3, -2-j4, -5-jl}

Now,

x(4-n) = {2-jl,4-j2,2-j2,2 + j3}^

X(4-fc) = {10-j2,-5-jl,-2-j4,5 + j3} I

Computing the DFT twice in succession

Another interesting property is obtained by computing the DFT twice in

succession.

x(N-n) = i(DFT(DFT(ar(

)))) = -i(DFT(X(fc)))

x{n) = l(DFT(X(AT-fc)))

If x{n) is even, then

x(n) = i(DFT(DFT(x(n)))) = i(DFT(X(*)))

Symmetry Properties 71

By substituting N

—

n for n in the IDFT equation, we get

x(N-n) = i E *(W

(JV_n)

* = ^ E

*(*«*,

n =

0,1,...N-l

k=0 fc=0

Example 4.7 The DFT of x(n) = {2 - jl,3 - j2,l + jl,2 + j3} is

X(k) = {8 + jl,-4- j3,-2-jl,6-

jl}.

If we compute the DFT of X(k)

and divide by N = 4, we get z(4 - n) = {2 - jl, 2 + j3,1 + jl, 3 - j2}. If

we compute the DFT of X(4 -

A;)

= {8 + jl, 6 - jl, -2 - jl, -4 - j3} and

divide by

= 4, we get x(n). I

This property brings out the almost duality of the time- and frequency-

domain sequences. If x(n)

•&

X(fc),then jjX(N=fn)

<S>

x(N±k). If x(n)

is even, then ^X{n) & x(k).

4.6 Symmetry Properties

The symmetry properties can be used to reduce the computational effort

and storage requirements in signal representation and manipulation. Be-

fore we describe these properties, some definitions of symmetry are given

for a periodic sequence of period N. A sequence is even-symmetric if

x(n) = x(N

—

n). For even N, an example of an even-symmetric sequence

is {9,1,5,3,7,3,5,1}. The values at the 0th and the yth positions can

be arbitrary. The other values are even-symmetric with respect to these

positions. A sequence is odd-symmetric if x(n) = —x(N

—

n). For even N,

an example of an odd-symmetric sequence is {0,1,4,3,0,

—3,

—4,

—1}.

The

values at the 0th and the ^th positions must be zero to satisfy the defini-

tion. The other values are odd-symmetric with respect to these positions.

A periodic sequence is even half-wave symmetric if x(n) = x(n ± y). A

periodic sequence is odd half-wave symmetric if x(n) = —x(n ± y). Conju-

gate or hermitian symmetry, x{n) = x*(N

—

n), implies that the real part is

even-symmetric and the imaginary part is odd-symmetric. Antihermitian

symmetry, x{n) = —x*(N

—

n), implies that the real part is odd-symmetric

and the imaginary part is even-symmetric.

Properties

the

DFT

Real signal

The definition

of DFT can be

rewritten expressing

x{n), X(k), and W#*

in terms

their real

and

imaginary parts

. . . 27T

(k)

jXi(k)

= 2J

(%r(n)

jxi(n))(cos jrnk

—

j sin

-rj-nk)

(4.1)

n=0

x(n) is

real,

its

imaginary parts

are

zero. Then,

Eq. (4.1)

reduces

JV-i

2TT 2TT

(A;)

jXi{k)

= y^

(n)(cos -Tr^A;

—

j'sin

-r^nk)

n=0

While

we are

going

establish mathematically,

it is

obvious that, since

the cosine

is an

even function

of k, the

real part

of the

spectrum

is an

even

function. Similarly, since

the

sine

is an odd

function

of k, the

imaginary

part

of the

spectrum

is an odd

function. Substituting

k = N

—

k, we get

JV-i

„ „

- k) +

jXi(N

-k)=Y^

(n)(cos jfn(N

-k)-j sin -n(JV - *))

n=0

Conjugating both sides

and

simplifying,

we get

Jv-i

2TT 2TT

—

jX{(N

—

k) = y^

ay(n)(cos — nk

—

j sin

—nfc)

n=0

= X

(k)+jXi(k)

(4.2)

Therefore,

(k) = X

{N - k) and X

{

{k) =

-Xj(iV

- fc). By

substituting

= f -

Jb,

we get X

(f -A) =

(f+k)

and X

(f -*) = -X

(% + k).

x(n) real^X(fc) hermitian

Example

4.8

x(n)

{2,1,4,3}

& X{k) =

{10,-2

j2,2,-2

- j2}

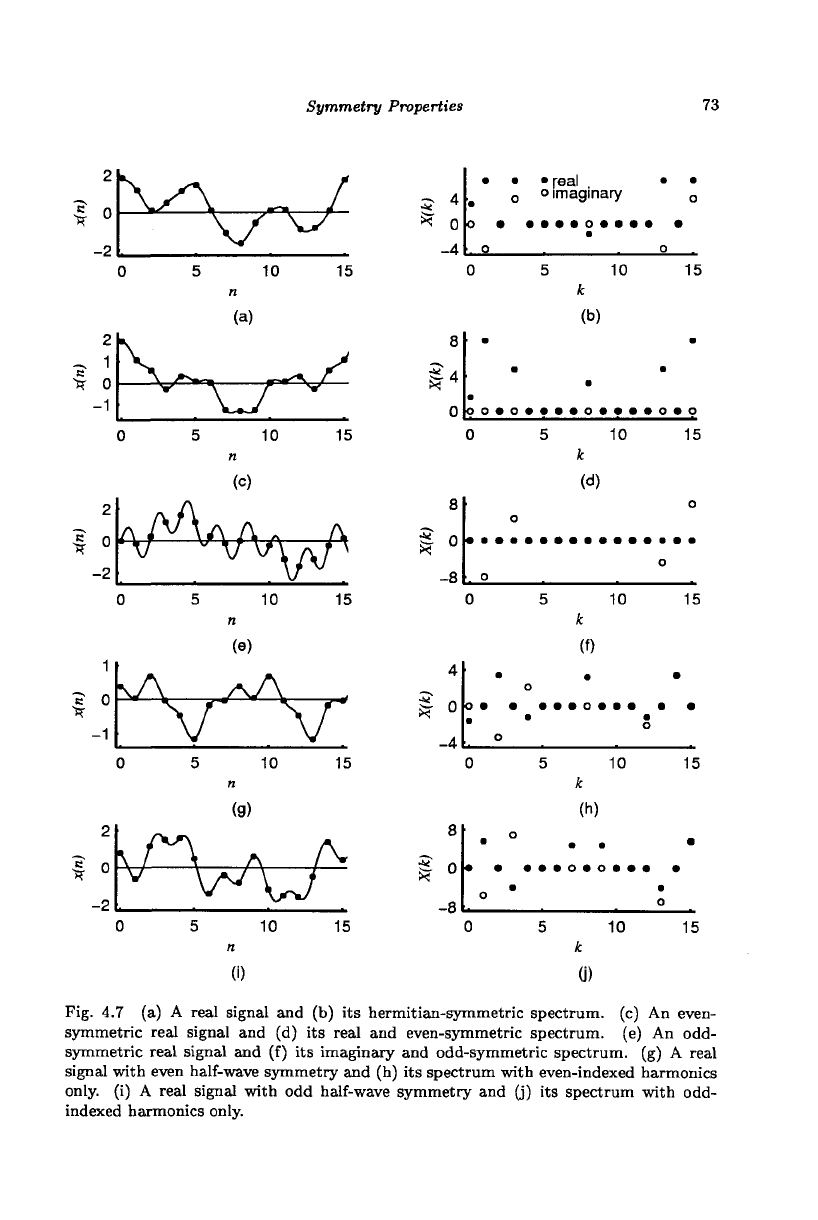
Figures 4.7(a)

and (b)

show, respectively,

arbitrary real signal

and its

hermitian-symmetric spectrum.

This symmetry implies that

the DFT

coefficients X(0),X(y),

and X(k),

= 1,2,..., y

—

1 are

sufficient

uniquely specify

the

spectrum

of a

real signal. Since

the

coefficients

X(0) and X(y) are

real,

for

even

and

the

rest

of the

required coefficients

are

generally complex,

total

of N

Symmetry Properties

•

• • peal

o imaginary

* °

8 . o

(d)

5 4

•

(b)

•

10 15

I °

(e)

10 15

0 o

(f)

S °

(g)

(h)

0* • •••o»o»»

10 15

(i)

Fig. 4.7 (a) A real signal and (b) its hermitian-symmetric spectrum, (c) An even-

symmetric real signal and (d) its real and even-symmetric spectrum, (e) An odd-

symmetric real signal and (f) its imaginary and odd-symmetric spectrum, (g) A real

signal with even half-wave symmetry and (h) its spectrum with even-indexed harmonics

only, (i) A real signal with odd half-wave symmetry and (j) its spectrum with odd-

indexed harmonics only.