Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

Properties of the DFT

4.14 Find the circular convolution of the frequency-domain sequences,

X(k) = {2+jl,l-j4,2+j5,3+j2}and#(fc) = {2+j3,l-j2, l-jl,2+j4}

using the DFT.

4.15 Find the circular cross-correlation of the time-domain sequences, x{n)

and h(n), using the DFT. Deduce the correlation of h(n) and x(n).

* 4.15.1 x(n) = {3,4, -1,2} and h(n) = {3,

-1,3,4}.

4.15.2z(n) = {2 + jl,l-j4,2 + j5,3+j2}and/i(7i) = {2 + j3,l-j2,l-

jl,2 + j4}.

4.16 Find the circular autocorrelation of the time-domain sequence using

the DFT.

4.16.1 x(n) =

{2,4,-1,2}.

4.16.2 x(n) = {j2,

j4,-jl,j2}.

4.16.3 x{n) = {2 + jl,

- j4,2 + j5,3 + j2}.

4.17 Find X(0) and X(4) with x(n) = {2 + jl, 1 - j4,2 + j5,3 + j2,3 -

j2,2-jl,l-j3,2+j2}.

4.18 Find x(0) and x(4) with X(k) = {2 - jl, 4 + j4,2 - j5,3 - j2,3 -

jl,2

jl,l-j3,2-j2}.

4.19 Let x(n) = {2 + jl,4 - j4,1 - j'5,3 - j2}. Compute X(k). Deduce

y(0),

Y(2), F(4), and F(6) from X{k) if j/(n) = {2 + jl,4- j4,l - j5,3-

j2,0,0,0,0}.

4.20LetX(ifc) = {2-jl,3-j4,l-;'5,3-j2}. Compute x{n). Deduce y(0),

y(2),

2/(4), and 2/(6) from x(n) if Y{k) = {2-

j'1,3-

j4,l - j5,0,0,0,0,3-

J2}.

4.21 Let x{n) = {2 + jl,4 - jl, 1 - j2,3 - j2}. Compute X(k). Deduce

y(fc)fromX(fc)if2/(n) = {2 + jl,0,4-jl,0,l-j2,0,3-j2,0}.

4.22 Let X(k) = {1 - jl, 2 - j4,1 - j5,3 + j2}. Compute x{n). Deduce

y(n) from x(n) if Y(k) = {1 - jl, 0,2 - j4,0,1 - j5,0,3 +

j2,0}.

4.23 Verify ParsevaFs relation.

* 4.23.1 x{n) = {1 - j3,1 + j4,1 - j2,3 - j2}.

4.23.2 x(n) = {1 - j3,1 + j4,1 - j2,3 - j2} and h(n) = {1 + j3,1 + jl,3 -

Ai-J'2}-

Chapter 5

Fundamentals of the PM DFT

Algorithms

If we compute the DFT or IDFT from definition, the computational com-

plexity is 0(N

) and they will not be efficient for signal analysis. Therefore,

the task now is to develop fast algorithms for these operations. Due to the

similarity of the DFT and the IDFT computation, a DFT algorithm can

be used to compute the IDFT with trivial modifications. Therefore, we

concentrate on the development of DFT algorithms.

The computation required for an TV—point DFT is the evaluation of N

sums,

each of N products. The data values are the same and a set of

twiddle factors is repeatedly used in forming the products for computing

each of the N sums. Therefore, there is a large amount of redundancy in the

computation. For example, with N = 8, the data sample x(l) is multiplied

by Wg and — W$ in order to compute the coefficients X(l) and X(5),

respectively. We can use any method to find the sum of products, but the

object is to reduce the number of multiplication and addition operations.

Typically, a multiplication operation is split and is carried out in stages. For

example, a multiplication by W^ is split into multiplications by W^ and

Wtf. This approach helps the usage of partial results for the computation

of more than one coefficient. A multiplication is carried out after adding

all possible terms. Now, the way to split the multiplications and share the

partial results is found using the DFT properties.

An alternate view of the problem of the computation of the DFT is

that a larger DFT is decomposed into a large number of smaller DFTs, in

particular into two-point DFTs, and the coefficients of the smaller DFTs

are combined to form the coefficients of the larger DFT. Again, the DFT

properties are used to find the procedure of decomposition and combina-

Fundamentals of the PM DFT Algorithms

tion. In short, the classical divide-and-conquer strategy of developing fast

algorithms is used.

In Sec. 5.1, first, we reformulate the DFT definition using vector input

and output quantities with each vector having two complex values. Then,

the reformulation is extended to any vector length. In Sec. 5.2, the direct

implementation of the reformulated DFT definition is described. In Sec. 5.3,

the reformulation of the IDFT definition in terms of vector quantities is

presented. The computation of the IDFT using DFT is described in Sec. 5.4.

In Sees. 5.5 and 5.6, the PM DIT DFT and the PM DIF DFT type of

algorithms, respectively, are developed for N = 8. In Sec. 5.7, the set of

PM DFT algorithms is classified.

5.1 Vector Format of the DFT

In order to derive more efficient DFT algorithms, we have to reformulate the

DFT definition using vector input and output quantities. Before we derive

the general form, let us consider the computation of a 4-point DFT using

input and output vector quantities, each with two elements. The definition

of a 4-point DFT to compute X(k) from x(n) is shown in matrix form

below, explicitly showing the half-wave symmetry of the twiddle factors.

*(0)1

X(l)

X{2)

X{2)\

• w

. w2

-w%

-wl

-w$

-w%

-wl

-w%

x(o)

x(l)

x(2)

1.3(3)

The half-wave symmetry of the twiddle factor matrix along the rows can

be used to rewrite the equation as

X(0)1

X(l)

X(2)

X(3)

w° •

-w2

-wl .

• a,(0) "

. a,(l) .

where a

(0) = x(0)+x{2), ai(0) = x(0)-x(2), a

(l) = a?(l) +

a;(3),

ai(l) =

a;(l)

—

x(3), and q = k mod 2. Let us say we want to compute the DFT of

x(n) = {2+jl,3—jl,4+j'2,

—1+J2}.

Then, the input vectors are given as

(n) = {(a

(0),

(0)),(ao(l),ax(l))} = {(6+A-2-jl),(2+iM-j3)}.

The half-wave symmetry of the twiddle factor matrix along the columns can

Vector Format of the DFT

o(0) = {o

(0),o

(0)} =

{s(0) + x(2),a;(0)-x(2)}

o(l) = {o

(l),o

(l)} =

{x(l) + x(3),x(l)-x(3)}

(a)

A(0) = {Ao{0)MO)} = {X(0),X(2)}

Ao(0) = a

(0)+a

(l)

(0) = a

(0)-a

(l)

il(l) =

{^,(l),A

(l)}

= {X(l),X(3)}

(l) = ai(0) + W

ai(l)

Ai(l) = ai(0)-W

ai(l)

(2 + jl)±(4 + j2) =

{6 + j3,-2-jl}

(3-jl)±(-l+j2) =

{2+jl,4-j3}

{8 + j4,4 + j2}

^b{-5-j5,l + j3}

(b)

Fig. 5.1 (a) The SFG for the computation of 4-point DFT using vectors of length two.

(b) A specific example of (a).

be used to rewrite the equation as

(0)

(1)

(-l)

a,(0)

(-l)

(l) J

where A

(0) = X(0), A^O) = X{2), A

{l)=X(l), Ai(l) = X(3), p = 0,1

and q

—

k mod 2. The matrix equation can be written in algebraic form as

MQ = £(-i)

a»wT*,

= o,i

(5.1)

n=0

where p = 0,1 and 9 = k mod 2. Equation (5.1) seems more complex than

the direct definition, Eq. (3.3). But it is actually easy and more efficient to

implement. For JV = 4, the definition of the DFT, Eq. (5.1), using vectors

itself is the optimum algorithm. The computation is shown in Figs. 5.1(a)

and (b) using a signal-flow graph (SFG).

The signal-flow graph

Although mathematical equations describe the DFT algorithms completely,

the SFG is the most convenient way to describe them as it gives all the de-

tails at a glance. The SFG depicts the process of combining the input values

to generate the output values using nodes and arrows. We describe here the

Fundamentals of the PM DFT Algorithms

SFG for the vector length of two. It consists of unfilled circles indicating

nodes,

and arrows indicating the signal flow path. Each node, except at the

beginning, represents an add-subtract operation. The nodes at the begin-

ning of a SFG just receive the input vector values. In Figs. 5.1(a) and (b),

the input vectors are placed close to the input nodes. The arrows terminat-

ing at an upper node originate from the nodes whose first element of their

vectors contributes to form the elements of the vector at the upper node

by add-subtract operation. The lower node receives the second elements

of its source vectors and the elements of the vector at a lower node are

also formed by add-subtract operation. At both type of nodes, the result

of the add operation forms the first element and the result of the subtract

operation forms the second element of the vector. Each data value along

an arrow is multiplied by a twiddle factor, W^, where N is the data length.

The exponent of the twiddle factor, s, is indicated close to the arrowhead.

No value or a zero near an arrowhead indicates that the value of the twiddle

factor is unity. Operations other than add-subtract and multiplication, and

any other objects will be indicated by special symbols.

The output vectors and the equations relating them to the input vectors

are shown at the output nodes in Fig. 5.1(a). Figure 5.1(b) shows the

operation of Eq. (5.1) for a specific example. Before we proceed to generalize

the DFT definition for any vector length, we try to answer the question

why do we usually use complex signals in DFT algorithms although we are

almost always interested in real signals.

Why do we use a complex signal

A complex signal is an ordered pair of real signals. For most part, we

are interested in processing real signals. But there is nothing wrong in

processing two real signals at a time if that procedure is advantageous. The

DFT of two real signals is combined in the DFT of a complex signal. The

individual DFTs can be split. If a signal is complex, its DFT is complex

whereas if it is real, its DFT is mostly complex. By keeping the input

and output values of the same (complex) type, we get algorithms that are

very regular and simpler. So much is the difference in the regularity and

simplicity, that although it may look odd, it is assumed that, in designing

DFT algorithms, the signal is complex as though the complex signal is

naturally occurring, but not the real signal. We can compute the DFT

with both the input and output quantities real. However, the algorithm

Vector Format of the DFT 99

will be irregular and practically inefficient. The reason is that representing

sinusoids by complex exponentials is natural and most efficient.

Vector format of the DFT

We present an equivalent vector format of Eq. (3.6) for any value of u,

where u is the vector length and it is a factor of N, the data length. For

following the derivation easily, apply each of the steps to the specific case

of TV = 8 and u = 2. The individual DFT equations with N = 8 are

given in Chapter 3. In addition, refer to the computation of the 4-point

DFT presented at the beginning of this section. Each sum of N products

in Eq. (3.6) can be rewritten as the sum of ^ products each of which is

formed using a sum of u products.

U—1 ,

U — 1 T.J

X(k) = W°

Y, x(0 + s-)W°

+Wk

(

N -+•" +

8=0 8=0

8=0

n=0 s=0 n=0 8=0

For each value of n, the inner summation is a u-point DFT and when

evaluated will give rise to u distinct values for k =

0,1,...,

—

1. Let

a(n),n =

0,1,...,

— 1

denote the nth input vector (Vectors will be shown

in boldface.) consisting of the u-point DFT values a

(n),

q =

0,1,...,

—

as defined below.

a(n) = {a

(n),ai(n),...A-iW}=Vi(n + 8-)B'

«,

—' u

8=0

0 = 0,1,...,u-l, n = 0,l,..., 1 (5.2)

Now, the last but one equation can be rewritten as

X(k) = J2 a

(n)W£

, fc = 0,l,...,iV-l

n=0

100

Fundamentals of the PM DFT Algorithms

Since the values of the u-point DFT a

(n) are periodic with a period of u,

for values of k equal to or greater than u, the values a

(n) repeat. Therefore,

q = k mod u

Replacing the variable k by k + p— in the last two equations, we get

£-1

X(k+p*) = ^ra,W^,i = 0,l,..,--l,

n=0

p =

0,1,...,

—

1, q = (k + p—) mod u

The N frequency coefficients X{k) can also be represented by ^ vectors

each with u elements. Let

A(k) = {A

(k),A

(k),...,A

(k)} = {X(k+p-)},

k =

0,1,...,

1, p =

0,1,...

,u - 1 (5.3)

With vector input quantities a

(n) as defined by Eq. (5.2) and vector output

quantities A

(k) as defined by Eq. (5.3), the DFT as defined by Eq. (3.6)

can be equivalently written as

(k)

= J2

(n)Wtf,

k =

0,1,...,

^ -

(5.4)

n=0

where q= (k+ p^) mod u and p =

0,1,...,

—

1. Thus, the use of vector

input and output quantities changes the form of the DFT definition from

Eq. (3.6) to Eq. (5.4).

Vector format of the DFT with u = 2

The use of vectors, each with two elements, provides the highest efficiency

since the frequency coefficients of a two-point DFT are the most closely

related. For the specific value of u = 2, Eqs. (5.2), (5.3), and (5.4) become,

respectively, as

N N

a(n) = {o

(n),ai(n)} = {x(n) + x(n+ -^),x(n) -x(n+ —)},

n = 0,l,...,y-l (5.5)

Direct Computation of the DFT with Vectors

101

A(k) = {MQMk)} = {X(k),X(k+ j)}, fc =

0,l,...,^-l

(5.6)

4(*) = £

(-l)

a„(n)WZ

k =

0,1,...,--

n=0

(5.7)

where p — 0,1 and q = (k + py) mod 2. The vector format definition of

the 8-point DFT with u = 2 is shown below in matrix form.

(0)

4,(1)

4(2)

4(3)

- wi

wi wi wi'

wi wi wi wi

. wi wi wi wi .

(-l)<*a,(0)

(-lWi)

(-1)

%(2)

(-l)

(3)

(5.8)

5.2 Direct Computation of the DFT with Vectors

In this section, we present an implementation of the DFT expression,

Eq. (5.7), for N that is an integral multiple of 4. It can be easily modified

for an even N. This implementation will be useful for testing programs. For

these lengths, this implementation is much more efficient than that given

in Chapter 3.

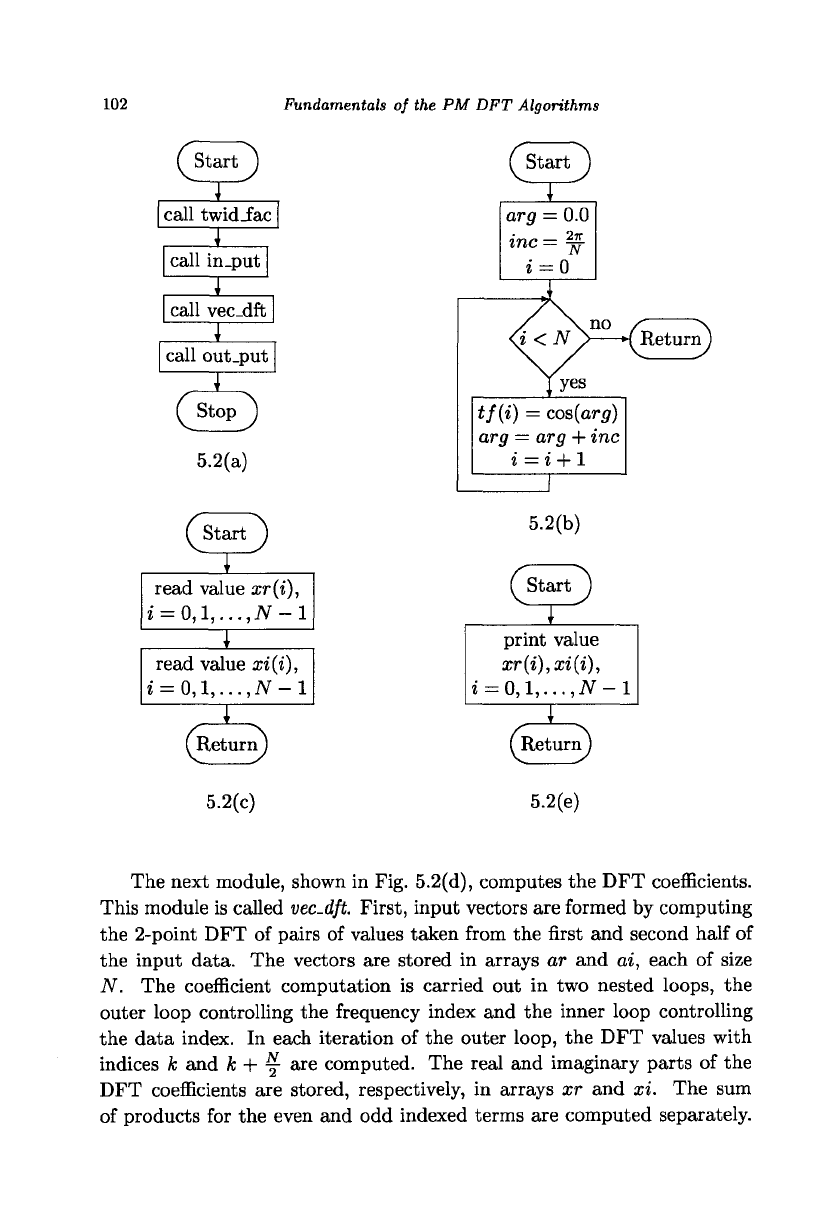
The main module, shown in Fig. 5.2(a), invokes four modules to get the

computation done. The second module, shown in Fig. 5.2(b), sets up the

twiddle factor array tf of size JV, that is the computation and storage of the

sample values of the cosine function over one cycle, with argument starting

from zero with increment of ^. This module is called twid-fac. Variable i

is used as a loop counter and the loop is terminated when i equals N, the

data size. The setting up of the twiddle factor array can be made faster by

using identities such as cos(^(iV

—

n)) = cos(^n). Note that this module

can be eliminated by computing the values of the twiddle factors each time

they are required. However, it is costly in terms of run-time.

The next module, shown in Fig. 5.2(c), reads the real and imaginary

parts of the complex input data, respectively, into the arrays xr and xi,

each of size N, the data size. It is assumed that the real parts of the input

data are stored before the imaginary parts in the input file. If the data is

real, initialize the values of the array xi to zero and read the data into the

array xr. This module is called in-put.

102 Fundamentals

of the PM DFT

Algorithms

( Start")

call twid_fac

call in.put

call vec_dft

call out_put

f Stop ^

5.2(a)

(start *)

read value ar(t),

i = 0,l,...,iV-l

read value

xi{i),

i =

0,l,...,N-l

(Return

('start

arp

= 0.0

—

2ff

= 0

{^ReturnJ

tf(i)

cos(arg)

arg

—

arg + inc

= i + l

5.2(b)

Tstart J

print value

xr(i),xi(i),

0,l,...,N-l

5.2(c)

(Return)

5.2(e)

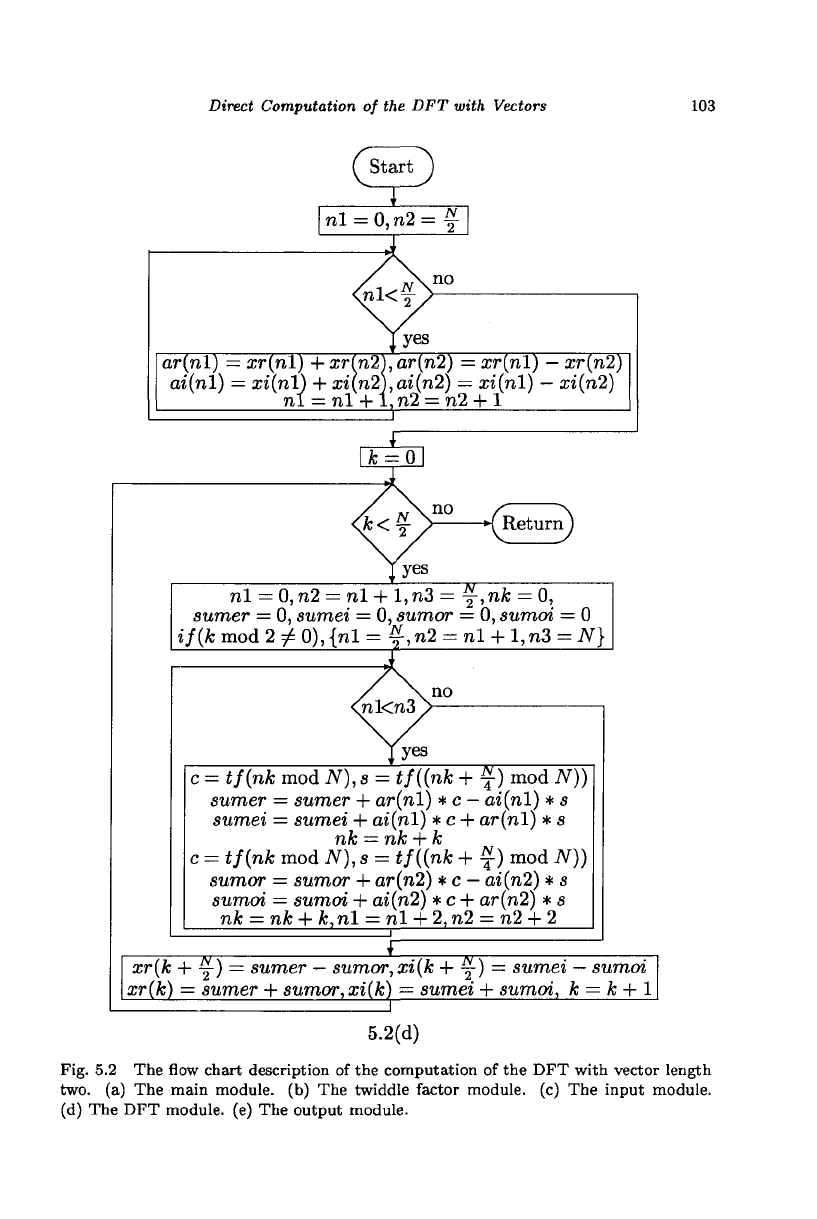
The next module, shown

Fig. 5.2(d), computes

the DFT

coefficients.

This module

called vec-dft. First, input vectors

are

formed

computing

the 2-point

DFT of

pairs

values taken from

the

first

and

second half

the input data.

The

vectors

are

stored

arrays

ar and ai,

each

size

N. The

coefficient computation

carried

out in two

nested loops,

the

outer loop controlling

the

frequency index

and the

inner loop controlling

the data index.

each iteration

of the

outer loop,

the DFT

values with

indices

and k + y are

computed.

The

real

and

imaginary parts

of the

DFT coefficients

are

stored, respectively,

arrays

xr and xi. The sum

of products

for the

even

and odd

indexed terms

are

computed separately.

Direct Computation of the DFT with Vectors

('start')

nl = 0,n2 =

ar(nl)

—

xr(nl) + xr[n2),ar(n2) = xr(nl)

—

xr{n2)

ai(nl) = xi(n

1) + xi(n2),ai{n2)

i,l = nl + l,n2 = r

= xi(nl)

—

xi(n2)

h2 + l

( Return)

nl = 0, n2 = nl + 1, n3 = y,nfc = 0,

sumer = 0, sumei = 0, sumor = 0, sumoi = 0

i/(fc mod 2 ^ 0), {nl = f, n2 = nl +

n3 = iV}

c = t/(n& mod iV), a = */((nfc + f) mod JV))

sumer = sumer + ar(nl) * c - oi(nl) * s

sumei = sumei + ai(nl) * c + ar(nl) * s

c = i/(nfc mod N), s = tf((nk + f) mod N))

sumor = sumor + ar(n2) * c

—

ai{n2) * s

sumoi = sumoi + ai(n2) *c + or(n2) * s

nk = nk + k, nl = nl +

n2 = n2 + 2

xr(k + ~) = sumer

—

sumor,xi(k + y) = sumei

—

sumoi

Tl^r

xr(k) = sumer + sumor,xi(k) — sumei + sumoi, k = k + 1

5.2(d)

Fig. 5.2 The flow chart description of the computation of the DFT with vector length

two.

(a) The main module, (b) The twiddle factor module, (c) The input module.

(d) The DFT module, (e) The output module.