Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

124

The u X 1 PM DFT Algorithms

comprise the input-output relation of a butterfly with p —

0,1,...,

—

However, the use of odd vector lengths is not preferred since it is less

advantageous.), can be deduced from Eqs. (6.3) and (6.4) as

r+1)

W = A^

modu

(h)

wsw^

modu

(i)

4+}\h)

modu

(h)

- WTO4?mod„(0

r+1)

(D = ^

+1)mod

Jh)

+ WZWl

W^Afi

odu

(l)

A^(l)

= A$

p+1)modu

(h)-W£WWA$

p+1)modu

(l),

(6.5)

where s is an integer whose value depends on the stage of computation

r and the index h, and p =

0,1,...,

—

1. Equation (6.5) characterizes

the u x 1 PM DIT DFT butterfly and represents u 2-point DFTs after the

input values indexed I are multiplied by appropriate twiddle factors. At a

time,

in the butterfly computation, we use only two vectors and the output

quantities can be overwritten in the locations of the input quantities as

they are no longer required. Therefore, only two indices are required which

are in general represented as h and I.

The computational stages

We have just split the problem into two (Eqs. (6.3) and (6.4)) in order to

form the output of the last stage. We assumed that the output vectors of

the previous stage are available. Next, we break each of the two problems of

the previous stage into two. Keeping on doing this, we get more and more

independent problems but each with a smaller size. We stop the process

of breaking down when each problem becomes a

1-vector

DFT. To reach

that level of decomposition, we need m stages of computation specified as

r =

1,2,...

,m, where m = log

^. As the number of problems increases,

the number of butterflies used to decompose each problem reduces in the

same proportion. Therefore, the number of butterflies remains the same in

each stage. Remember that two vectors are processed in a butterfly and

we have ^ vectors in any stage. Therefore, the number of butterflies that

constitutes a stage is ^. Only the grouping of the butterflies changes from

stage to stage. In the last stage, the twiddle factor exponent s is the same

as the index h. And it is true for any stage provided the base N in WN

is changed according to the stage. As we want to use one set of twiddle

factors, we generate them only with the base TV. Therefore, instead of

varying the base N, we multiply the exponent by 2 for each stage. As the

The 2 x 1 PM DIT DFT Algorithm

125

size of the problem is reduced, the difference between the indices h and /

is also reduced by a factor of two. The expressions for the twiddle factor

exponent and the indices of the nodes of each group of butterflies are given

as follows.

h = imod2

, z =

0,1,...,

^ - 1

/ = h + r-

(6.6)

a = h(2

)

Using the expressions given above, algorithms can be derived for any value

of N and u for which ^ is an integral power of 2. As a consequence of

splitting the even and odd indexed input vectors over m stages, the input

vectors to the first stage are placed in the bit-reversed order.

6.2 The 2x1 PM DIT DFT Algorithm

The specific algorithm with u = 2, that is each vector with two complex

elements, is practically very useful. Therefore, we give a detailed description

of this algorithm.

The 2x1 PM DIT DFT butterfly

The butterfly input-output relations at the rth stage can be obtained, by

substituting u = 2 in Eq. (6.5), as

r+1)

W = A$\h) +

A%\l)

\h) = 4\h)-W^\l)

r+1)

<*4

\l) = AP(h)-W

*AP(l),

where s is an integer whose value depends on the stage of computation r and

the index h. These equations characterize the 2x1 PM DIT DFT butterfly

shown in Fig. 6.1. This butterfly computes two 2-point DFTs after the

input values indexed I are multiplied by appropriate twiddle factors. The

butterfly structure comprises two input nodes, at each of which it receives

the two complex numbers of an input vector. The input vector at the upper

node is A^

'(h) and its elements are A£'(h) and AY'(h). The input vector

at the lower node is A^

'(l) and its elements are A£'(l) and A{ >(l). The

first and second elements of A^

' (I) are multiplied, respectively, by twiddle

126 The u x 1 PM DFT Algorithms

= {A^(h),A[

\h)} o^- *^o = {A^

\h),A[

r+1

\h)}

= {4

(0,4

(0} o^ >> ={k

+1)

d),A

r+1

\i)}

Fig. 6.1 The SFG of the butterfly of the 2 x 1 PM DIT DFT algorithm, where 0 < s <

^-. Twiddle factors are represented only by their exponents. The symbol s represents

factors W^ and

{-j)W

to produce

A<£\l)

and (-j)W^

(Z). Only

one of the two twiddle factors needs to be generated as they are trivially

related. The two-point DFT of (A^ (h), W^A^ (I)) constitute the first and

the second elements, respectively, of the butterfly output vector A^

r+1

'(h)

at the upper output node. The two-point DFT of (A[

(h),

(-j)Wfr

{

]

(/))

constitute the first and the second elements, respectively, of the butterfly

output vector A^

r+1

'(l) at the lower output node.

The computation involved in a butterfly includes 2 complex multiplica-

tions,

each requiring two real additions and four real multiplications, and

two 2-point DFTs, each requiring four real additions. Four complex num-

bers or eight real numbers are loaded and stored. Therefore, a butterfly re-

quires 8 real multiplications, 12 real additions, and, assuming that sufficient

number of registers is available in the processor, 16 data transfer operations

between the memory and the processor (The loading of the twiddle factors

is ignored since it occurs once for a set of butterflies and amounts to less

than N data transfers, whereas the number of load and store operations for

the data is a function of N log

N.). While the computation of two 2-point

DFTs is required in all the butterflies, the complex multiplication operation

requires fewer number of real operations for some butterflies. These spe-

cial butterflies requiring reduced computation are with s = 0 and s = ^-.

The first special butterfly requires 8 real additions while the second special

butterfly requires 4 real multiplications and 12 real additions.

The computational stages

The number of 2 x 1 PM DIT butterflies in each of the m stages is ^.

For example, with N — 16, there are 3 stages specified as, r = 1,2, and

Four butterflies make up a stage. Indices h and I, and the twiddle

The 2 x 1 PM DIT DFT Algorithm

127

Fig. 6.2 The SFG of the 2 x 1 PM DIT DFT algorithm, with N = 16. Twiddle factors

are represented only by their exponents. For example, the number 4 represents Wj

factor exponent s for each group of butterflies are given, respectively, by

(h = i mod 2

-\ i =

0,1,...

,3), I = h + 2

-\ and s =

h(2

The SFG

of the 2 x 1 PM DIT DFT algorithm, with N = 16, is shown in Fig. 6.2.

The three stages are demarcated by unfilled circles. Except for the last

stage, the output vectors of a butterfly are the input vectors for butterflies

of the succeeding stage.

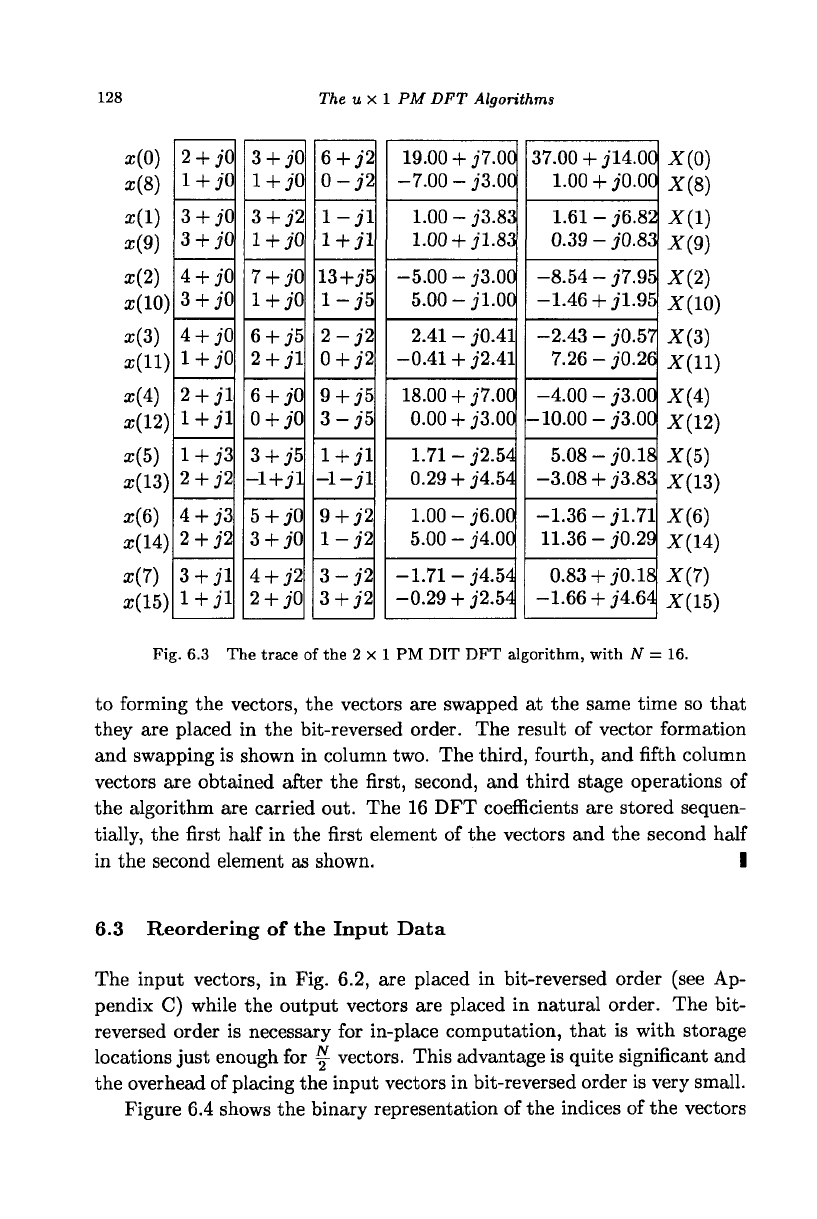
Example 6.1 Figure 6.3 shows the trace of the algorithm shown in

Fig. 6.2. The values, given to a precision of two decimal places, were ob-

tained from running a program with a much higher precision. The first

column values are 16 complex input values to the DFT. The input values

are stored sequentially in the storage locations assigned for 8 vectors each

with 2 complex elements, the first half values in the first element of the vec-

tors and the second half values in the second element. Vectors are formed

by adding and subtracting the elements stored in the individual vector lo-

cations. For example, the elements of the vector in the first row of the

second column are (2 + jO) + (1 + JO) and (2 + jO) - (1 + JO). In addition

128

The u X 1 PM DFT Algorithms

x(0)

x(8)

x(l)

x(9)

x{2)

x(10)

x(3)

ar(ll)

s(4)

x(12)

s(5)

x(13)

*(6)

x(14)

x(7)

z(15)

2 + jO

1+jO

3 + jO

4 + jO

3 + jO

4 + jO

1+jO

2 + jl

1+jl

1+J3

2 + J2

4 + J3

2 + J2

3 + jl

1+jl

3 + jO

1 + jO

3 + J2

1 + jO

7 + jO

1 + jO

6 + j5

2 + jl

6 + jO

0 + jO

3 + J5

-1+jl

5 + jO

3 + jO

4 + J2

2 + jO

O OS

Vs. Vs.

to to

1-jl

1+jl

13+J5

1-J5

2-J2

0+J2

9+j5

3-J5

1+jl

-1-jl

>_i

Vs. Vs.

to to

CO CO

+ 1

Vs. Vs.

to to

19.00 + J7.00

-7.00 - J3.00

1.00 - J3.83

l.OO + jl.83

-5.00 - J3.00

5.00 - jl.00

2.41 - J0.41

-0.41 + J2.41

18.00 + J7.00

0.00 + J3.00

1.71 - J2.54

0.29 + J4.54

1.00 - J6.00

5.00 - J4.00

-I.71-j4.54

-0.29 + J2.54

37.00 + J14.00

1.00 + jO.OO

1.61-J6.82

0.39 - jO.83

-8.54 - J7.95

-1.46 + J1.95

-2.43 - jO.57

7.26 - jO.26

-4.00 - J3.00

-10.00-J3.00

5.08 - jO.18

-3.08 + J3.83

-1.36-jl.71

11.36 - jO.29

0.83 + J0.18

-1.66 + J4.64

X(0)

X(8)

X(l)

X{9)

X{2)

XilO)

X{2)

X(ll)

X(4)

X(12)

X(5)

X(13)

X(6)

X(14)

X(7)

X(15)

Fig. 6.3 The trace of the 2 x 1 PM DIT DFT algorithm, with N = 16.

to forming the vectors, the vectors are swapped at the same time so that

they are placed in the bit-reversed order. The result of vector formation

and swapping is shown in column two. The third, fourth, and fifth column

vectors are obtained after the first, second, and third stage operations of

the algorithm are carried out. The 16 DFT coefficients are stored sequen-

tially, the first half in the first element of the vectors and the second half

in the second element as shown. I

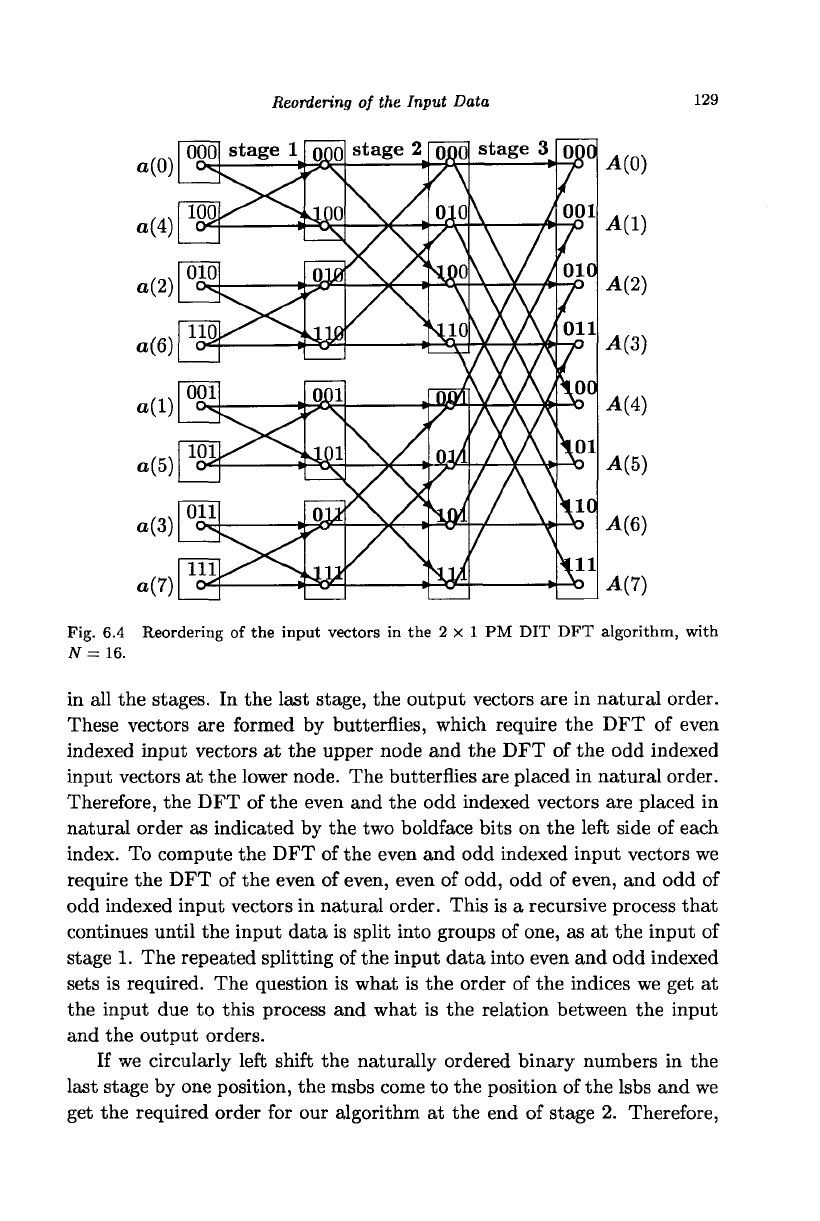
6.3 Reordering of the Input Data

The input vectors, in Fig. 6.2, are placed in bit-reversed order (see Ap-

pendix C) while the output vectors are placed in natural order. The bit-

reversed order is necessary for in-place computation, that is with storage

locations just enough for y vectors. This advantage is quite significant and

the overhead of placing the input vectors in bit-reversed order is very small.

Figure 6.4 shows the binary representation of the indices of the vectors

Reordering of the Input Data

129

Fig. 6.4 Reordering of the input vectors in the 2 x 1 PM DIT DFT algorithm, with

N = 16.

in all the stages. In the last stage, the output vectors are in natural order.

These vectors are formed by butterflies, which require the DFT of even

indexed input vectors at the upper node and the DFT of the odd indexed

input vectors at the lower node. The butterflies are placed in natural order.

Therefore, the DFT of the even and the odd indexed vectors are placed in

natural order as indicated by the two boldface bits on the left side of each

index. To compute the DFT of the even and odd indexed input vectors we

require the DFT of the even of even, even of odd, odd of even, and odd of

odd indexed input vectors in natural order. This is a recursive process that

continues until the input data is split into groups of one, as at the input of

stage 1. The repeated splitting of the input data into even and odd indexed

sets is required. The question is what is the order of the indices we get at

the input due to this process and what is the relation between the input

and the output orders.

If we circularly left shift the naturally ordered binary numbers in the

last stage by one position, the msbs come to the position of the lsbs and we

get the required order for our algorithm at the end of stage 2. Therefore,

130

The u x 1 PM DFT Algorithms

the lsbs of the new order are fixed and again we circularly left shift the

two sets of numbers with two boldface bits to get the proper order at the

end of the stage 1. Now the position of the second bit gets fixed. Only

one bit, shown in boldface, remains to be considered and, as shifting one

bit makes no difference, we get the input order. Circularly left shifting by

one bit repeatedly, the first time we made the msbs of the natural order as

the lsbs of the new order, the second time we moved the bits next to the

right of msbs in the natural order to the left of lsbs in the new order, and

finally we left the lsbs of the natural order in the msb positions of the new

order. The net result is that we have reversed the position of the bits in

the natural order.

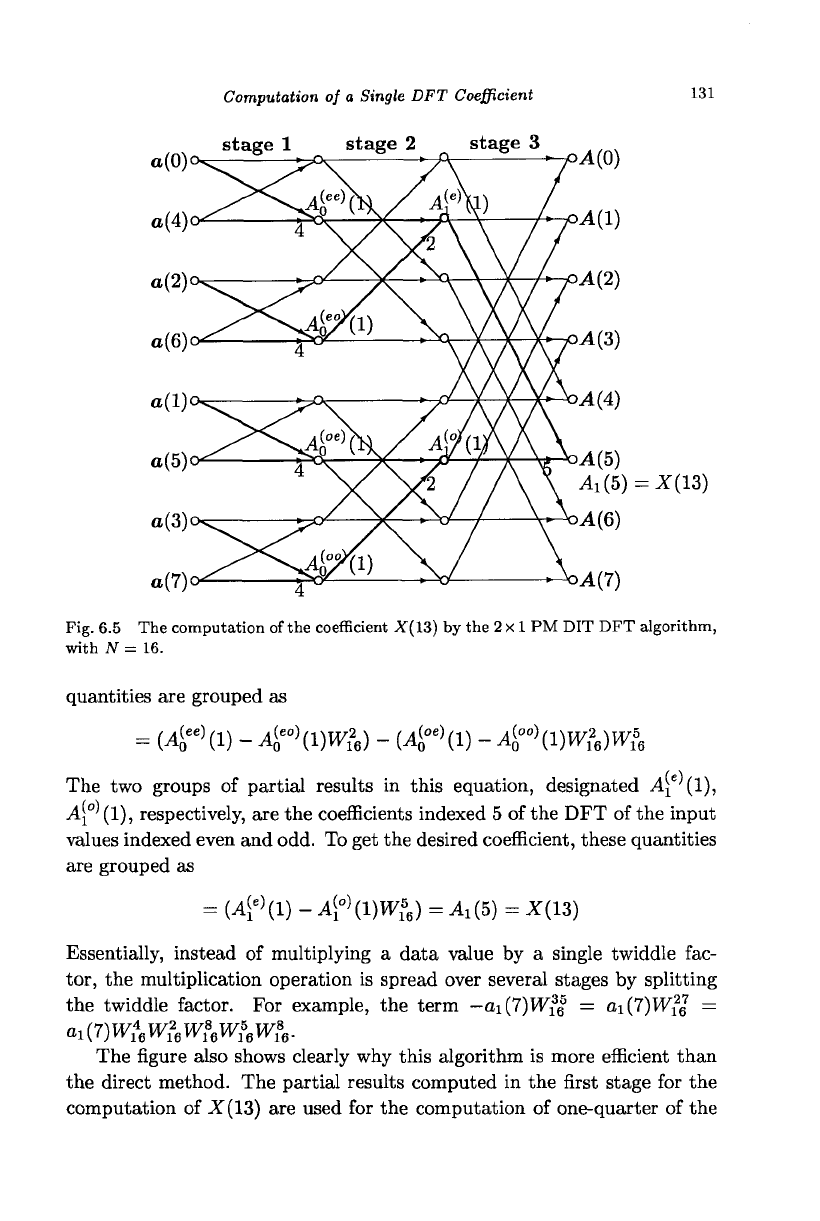
6.4 Computation of a Single DFT Coefficient

To get further insight into the algorithm, let us consider how a specific

coefficient is computed. By highlighting the relevant signal flow paths, we

have shown the grouping of partial results and multiplication by common

factors in the computation of X(13) in Fig. 6.5. By definition,

X(13) = ^(5) = 5^(-l)

(n)W

n=Q

= a, (0) - oi (1) Wft + oi (2) Wft

- oi (3)

{4)W™ -

(5)W?i + oi(6)W-§» -

(7)W?

This computation is split over three stages. At the end of the first stage,

we get

= MO) + ^(4)0 - M2) + ai(6)W?

)W?

- Ml) + «i(5)^i

)^i

+ (oi(3) + ai(7)W?

)W7e

This grouping and finding common factors is continued. Eventually, the

number of groups is reduced from y to one. The four groups of partial

results in this equation, designated ^(l).^"^

).^^

).^

spectively, are the coefficients indexed 1 of the DFT of the input values

indexed even of even, even of odd, odd of even, and odd of odd. These

Computation of a Single DFT Coefficient

131

stage 1 stage 2

stage 3

A(0)

A{1)

A(2)

A{3)

A(4)

A(5)

A!(5) = X(13)

A(6)

A(7)

Fig. 6.5 The computation of the coefficient X(13) by the 2 x 1 PM DIT DFT algorithm,

with N = 16.

quantities are grouped as

= (4

ee)

(i) - 4

eo)

) - (4

oe)

(i) - 4

00)

(i)w?«)n

The two groups of partial results in this equation, designated

'(l),

(1), respectively, are the coefficients indexed 5 of the DFT of the input

values indexed even and odd. To get the desired coefficient, these quantities

are grouped as

= (A|

(l) - 4°Hl)W*

) = A

(5) = X(13)

Essentially, instead of multiplying a data value by a single twiddle fac-

tor, the multiplication operation is spread over several stages by splitting

the twiddle factor. For example, the term -ai(7)W^| = ai(7)W™ =

aMW&W&W&W&W?,.

The figure also shows clearly why this algorithm is more efficient than

the direct method. The partial results computed in the first stage for the

computation of X(13) are used for the computation of one-quarter of the

132 The u x 1 PM DFT Algorithms

DFT coefficients. Second stage partial results are used to compute one-

eighth of the DFT coefficients and so on. This sharing of the partial results

contributes to the reduction of the computation compared with the direct

computation since, in that case, no sharing is done.

Seven complex multiplications and fifteen complex additions are re-

quired to compute a single coefficient. The multiplications in the first stage

are trivial. The number of multiplications in the other stages is ^

—

1. In

the second stage, the complex multiplication requires less computational

effort. Compare this with N complex multiplications required in the direct

computation of the DFT. The reduction of the number of multiplications

reduces the round-off errors. The spreading of the computation over several

stages also reduces the errors and makes the scaling problem less severe in

fixed-point implementations.

The DFT algorithms are so efficient that, unless we want to compute

very few coefficients, it is better to use an algorithm to compute all the

coefficients even if all of them are not required. To compute a single DFT

coefficient, we have to use the appropriate computational path in the SFG of

an algorithm. This method is more efficient than using the DFT definition

because the computational effort is reduced by more than half in terms of

arithmetic operations. In addition, we have to compute very few twiddle

factors.

6.5 The u X 1 PM DIF DFT Algorithms

The DIT algorithm, just described, is based on splitting a set of input

vectors into two groups, computing their DFTs separately, and combining

the two DFTs to get the DFT of the input data. The DIF algorithms , on

the other hand, are based on combining the first- and second-half of the

input vectors to make two independent sets of input vectors and computing

their DFTs separately to get the even and odd indexed DFT vectors of the

input data. The DIT and DIF algorithms are dual and one can easily be

deduced from the other.

Decomposing the summation in Eq. (5.4) corresponding to those of the

first- and the second-half of the input vectors a

(n) yields

(k)= £

(n)WZ

]T W^a,(

)^,

n=0 „=£

The nxl PM DIF DFT Algorithms

133

where q = ((k + p~) modu), k =

0,1,...,

^ - 1, and p = 0,

l,...,u

- 1.

Replacing n by n + |jj in the second summation on the right side gives

{k)=

£ Wra

(n)WZ

+ £

{n+

^)W^

n=0 n=0

2u''

,JV

The pair of summations can be combined into a single one, giving

JV__1

2u *•

(k)

= Y, Wr(a

(n) +

W^Wpa

+ ^)«* (6.8)

n=0

The even and odd indexed DFT values A

(k) are readily obtained from

Eq. (6.8) by replacing

with 2k and k with 2k + 1, respectively.

N--1

(2k)

= £ Wr(a

(n) + wi

k+p&)

(n +

^))Wf,

n=0

q = (2(k + p—)) mod u (6.9)

r-l

(2k

+ 1)=£ WT(o,(

) +

W^^W^in

+ —

))W%Wf,

71=0

q = (2(A; +p—) + 1) mod u, (6.10)

where k =

0,1,...,

—

1 and p =

0,1,...,

—

1. The problem of comput-

ing an ^—vector DFT, therefore, has been decomposed into a problem of

computing two ^ —vector DFTs.

The u X 1 PM DIF DFT butterfly

In general, the input-output relations of the butterfly computation at the

rth stage, for an even vector length, can be deduced from Eqs. (6.9) and

(6.10) as

r+1

\h) = a$

modu

(h)+WZa%

modu

(l)

a™(h) = a%

modu

(h)-WZa$

modu

(l)

+1)

(0 = WhaV

mod

Jh) + WtW}

W^Z\

+1)modu

(l)

{

}

^(1) =

q+l)

mod u

(h) -

W<W}

q+1)

mod

„(/),