Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

154

The 2 x 2 PM DFT Algorithms

Fig. 7.1 The SFG of the butterfly of the 2 x 2 PM DIT DFT algorithm, where 0 < s <

4r. Twiddle factors are represented only by their exponents. The symbol s represents

The computational stages

There are m stages specified asr = l,2,...,m, where m = log

y. Starting

from the output side, pairs of adjacent stages are formed each using ^2x2

PM DIT butterflies. If m is odd, f 2 x 1 PM DIT butterflies are used

for the first stage. The expressions for the twiddle factor exponent and

the indices of the nodes of each group of butterflies are given as follows:

hi = i mod 2

, i =

0,1,...,

f -1,11 = hl + l(2

), hi = hl +

2(2

12 = hl + 3(2

r_2

), and s = /il(2

m_r

), where r is the stage number of the

second of the two adjacent stages combined. The SFG of the 2x2 PM DIT

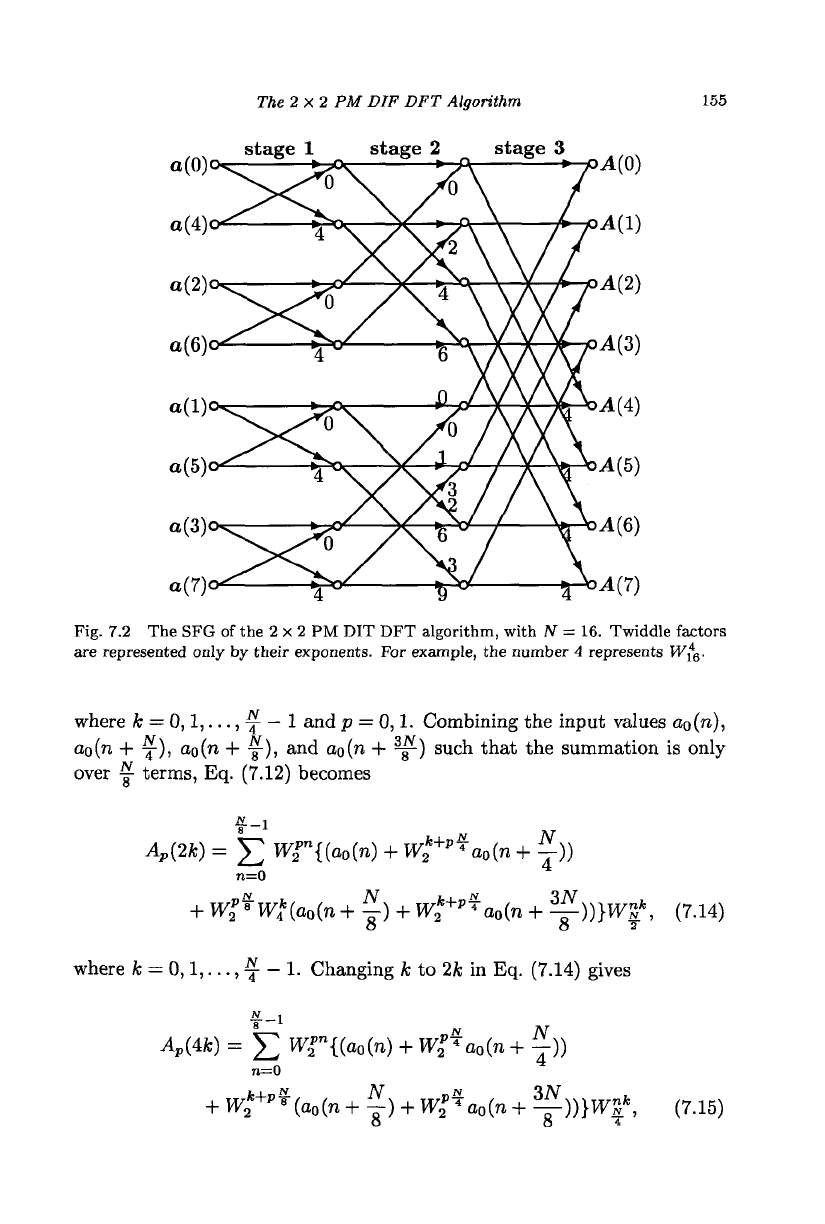
DFT algorithm with N = 16 (m = 3) is shown in Fig. 7.2.

7.2 The 2x2 PM DIF DFT Algorithm

To derive the 2x2 PM DIF DFT algorithm, consider the decomposition

of an Y

_vector

DFT into two ^-vector DFTs in the first stage of the 2x1

PM DIF DFT algorithm. Equations (6.9) and (6.10) of the uxlPM DIF

algorithm, with u

—

2, is given as

(2k)

= J2 Wr{aoN + wf

+pf

(n+ j)}Wf (7.12)

n=0

f-1

(2k

+ 1) = Y^ Wi

(n) +

^Wla

+ -)}W^Wf ,(7.13)

n=0

The 2x2 PM DIF DFT Algorithm

stage 1 stage 2 stage 3

155

A(0)

A(l)

A(2)

A(3)

A(i)

A(5)

A(6)

%*>M7)

Fig. 7.2 The SFG of the 2 x 2 PM DIT DFT algorithm, with N = 16. Twiddle factors

are represented only by their exponents. For example, the number 4 represents W*

where fc = 0,l,...,^

—

1 andp = 0,1. Combining the input values a,o(n),

ao(rc +

;

f-), ao(n + y), and ao(n + ^) such that the summation is only

over Y terms, Eq. (7.12) becomes

8 -

(2k)

= £ W

{Mn) +

+ ^))

n=0

+ W

* W

*(oo(n + £) + W*

+pf

(n + ^))}W£*, (7.14)

o o 2

where k =

0,1,...,

^ - 1. Changing

to 2k in Eq. (7.14) gives

(4fc) = £ WriMn) +

W^a

(n+

^))

n=0

+ W

fe+pf

(ao(n+^) + <^a

(n+^))}W|

, (7.15)

156 The 2 x 2 PM DFT Algorithms

where

0,1,...,

y - 1. Replacing k by

2A;

+ 1 in Eq. (7.14) yields

(4A; + 2)= 53 Wi

{(a

(n) -

W^ao(n

+ ^))

n=0

+ W*^*^(ooCn + y) - <

(n +

™))}Wf?Wf,

(7.16)

where

0,1,...,

y - 1. Rewriting Eq. (7.13) such that the summation

is only over j- terms yields

-l

(2k

+ 1)=£ Wr

{(ai(n) + W

+PT

oi(n +£))

n=0

+ <• WtfWftaiC" +^) + W*

V(r*+^))TOW^,(7.17)

O 0 2

N. jfe

«. , 37V

-j) + W

+Pi

(n+—

where

0,1,...,

^ - 1. Changing k to 2fc in Eq. (7.17) gives

f—I

(4A:

+ 1)=£ W

"{(ai(n) + W^W^n + £))

n=0

+ W*

•

W2(

(n +j) + wf* Wl

{n +

™))}WZWf,

(7.18)

where

—

0,1,...,

- 1. Replacing

2A:

in Eq. (7.17) yields

(4A:

+ 3)=£ Wi

{(

(n)-W^W\a^n +j))

n=0

+ W^WlWHa^n +*L)-WZ*Wla

(n +^-))}W%

Wt ,(7.19)

O O 4

where k =

0,1,...,

y - 1.

The 2x2 PM DIF DFT Algorithm 157

The 2x2 PM DIF DFT butterfly

The input-output relation of a butterfly of the 2x2 PM DIF algorithm can

be deduced from Eqs. (7.15), (7.16), (7.18), and (7.19) as

r+1)

(w)

p+1)

(W)

{

;

\h2)

r+1)

(fc2)

{

;

\n)

r+1)

(/l)

r+1)

(<2)

+1)

(Z2)

r+2)

(»D

(hl)

«r

ci)

r+2)

(Zl)

r+2)

(M)

r+2)

(/i2)

(/2)

r+2)

(Z2)

= 4

(w)+4

(M)

= 4

(w)-4

(w)

= <4

(/il) + w|<4

(Zi2)

= aj

(M)-W$aj

(/»2)

= 4

(U)+a«(/2)

= 4

(n)-aW(/2)

= aj

(n) + w|a[

(J2)

= 4

(/l)-wlot

(Z2)

= ai

r+1

\hl)

a£

\ll)

= a£

\hl) - a£

\ll)

= Wf?a[

r+1

\hl)

*a<r

\ll)

= Wfta[

r+1

\hl)-W

*a<f

\ll)

= wU

r+1)

m+w?*a£

Hi2)

\h2)-W

^a^

\l2)

°a<f

\h2)

8+3

-?a?

\l2)

= Wfra^m-W^a^W,

where s is an integer whose value depends on the stage of computation r

and the index hi. The 2 x 2 PM DIF DFT butterfly is shown in Fig. 7.3.

The butterfly computes eight 2-point DFTs along with the multiplication of

the input values by appropriate twiddle factors. The number of operations

in the DIF butterfly is the same as that in the DIT butterfly.

The computational stages

There are m stages specified as r =

1,2,...,

m, where m = log

y. Starting

from the input side, pairs of adjacent stages are formed using |2x2 PM

DIF DFT butterflies. If m is odd, f- 2 x 1 PM DIF DFT butterflies are

used for the last stage. The expressions for the twiddle factor exponent and

the indices of the nodes of each group of butterflies are given as follows:

(hi = i mod

i =

0,1,...,

f - 1), Zl = hi + l(2"

), h2 =

158 The 2 x 2 PM DFT Algorithms

aW(M)Or ^hU ^o

(hl)

4oa(

+V(l2)

Fig. 7.3 The SFG of the butterfly of the 2 x 2 PM DIF DFT algorithm, where 0 < s <

y. Twiddle factors are represented only by their exponents. The symbol s represents

hi +

2{2

I2 = hl+ 3(2

), s = hl(2

), where r is the stage

number of the first of the two adjacent stages combined. The SFG of the

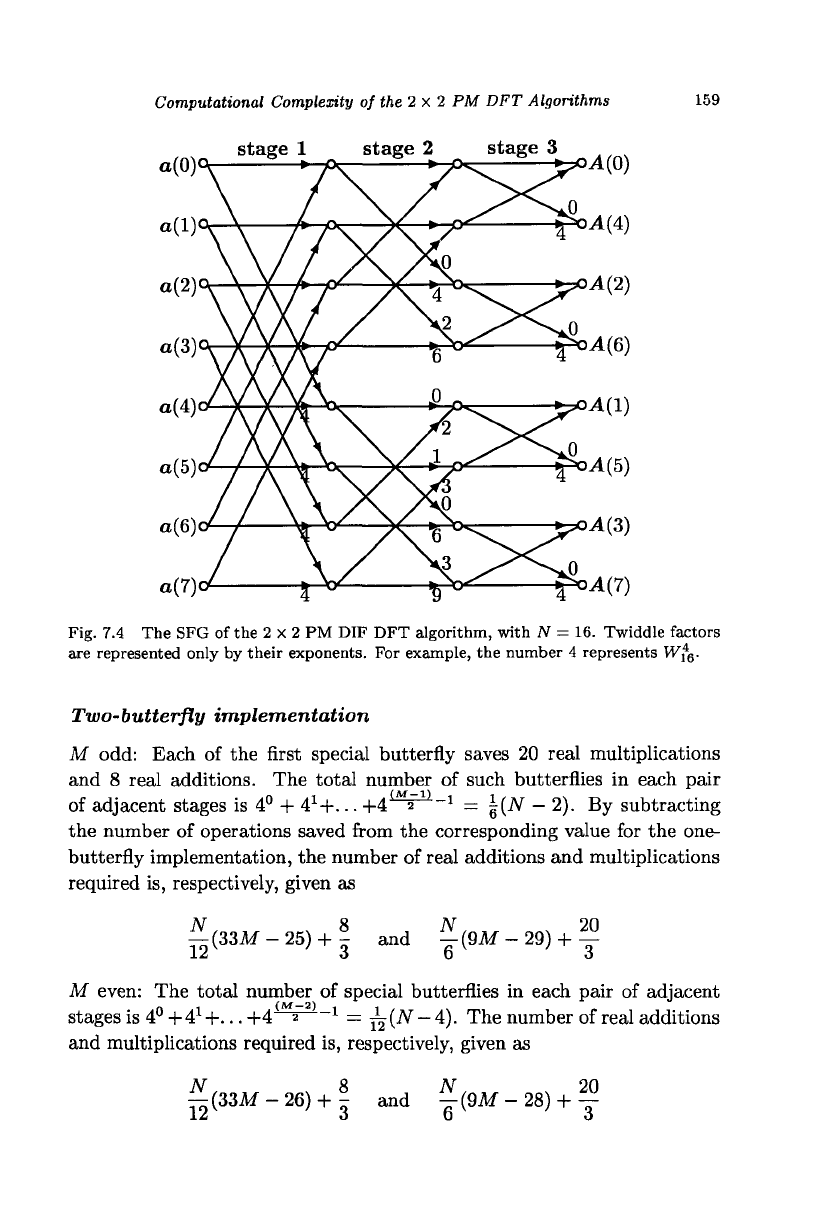
2 x 2 PM DIF DFT algorithm with N = 16 (m = 3) is shown in Fig. 7.4.

7.3 Computational Complexity of the 2 x 2 PM DFT

Algorithms

One-butterfly implementation

M = log

N, odd: There are j- butterflies in each of the ^-^- combined

stages. Each butterfly requires 24 real multiplications and 44 real additions.

The vector formation stage requires 2N additions. The number of real

additions and multiplications required is, respectively, given as

N(M-l)

„

Ar AT

(llM-3) , N(M-l)

3^,,, ,,

— ^

'-M + 2N = N± '- and — '-2A= -N(M -I)

8 2 4 8 2 2

M even: There are y butterflies in each of the ^f^- combined stages. The

vector formation and first stages require 4N additions. The number of real

additions and multiplications required is, respectively, given as

N{M-2)..

... ..(11M-6) , N{M-2)

3.....

;

44 + 4iV = A^ '- and —

24 =-iV(M - 2)

Computational Complexity of the 2 x 2 PM DFT Algorithms 159

Fig. 7.4 The SFG of the 2 x 2 PM DIF DFT algorithm, with N = 16. Twiddle factors

are represented only by their exponents. For example, the number 4 represents Wf

Two-butterfly implementation

M odd: Each of the first special butterfly saves 20 real multiplications

and 8 real additions. The total number of such butterflies in each pair

of adjacent stages is 4° + 4

+... +4 a"

= |(iV - 2). By subtracting

the number of operations saved from the corresponding value for the one-

butterfly implementation, the number of real additions and multiplications

required is, respectively, given as

N 8 N 20

_(33M-25) + - and -(9M-29) + -

M even: The total number of special butterflies in each pair of adjacent

stagesis4° + 4

+. ..+4 2

—

^(N-4).

The number of real additions

and multiplications required is, respectively, given as

— (33M-26) + - and -(9M-28) + y

160

The2x2 PM DFT Algorithms

Table 7.1 Figures of Computational Complexity for the 2x2 PM DFT Algorithm with

Various Number of Butterflies.

Number of multiplications | Number of additions

128

256

512

1024

2048

4096

1-B_fly

192

384

1152

2304

6144

12288

30720

61440

2-B_fly

284

732

1884

4444

10588

23900

54620

3-B_fly

264

712

1800

4360

10248

23560

53256

1-B_fly

152

416

960

2368

5248

12288

26624

60416

129024

3-BJ

144

376

920

2200

5080

11608

25944

57688

126296

Three-butterfly implementation

M odd: Each of the second special butterfly saves 4 real multiplications.

The total number of such butterflies in each pair of adjacent stages is 4° +

4}+...

+4 a

= ^j(iV—8). The number of real multiplications required

is given as iV(|M

—

5) +

The number of real additions remains the same

as in the case of the 2-butterfly implementation.

M even: The total number of special butterflies is ^(N

—

4). The number

of real multiplications is the same as in the case of M odd.

The number of each of the two operations of real multiplication and real

addition required by the 2x2 PM algorithms for various values of N and

for various number of butterflies is given in Table 7.1. The implementation

of the 2x2 PM DFT algorithms consists of a three-loop construct that is

similar to the implementation of the 2x1 PM DFT algorithms.

Twiddle factor generation

The twiddle factors for the general butterflies with indices h and

- h

for the DIT algorithms (h and ^h - h for the DIF algorithms) are triv-

ially related and, therefore, they need to be computed or referenced only

once if the butterflies are processed at the same time. The twiddle fac-

tors of the first butterfly are of the form Wft, Wjf, W%

, W£

, and

, whereas they are of the form W$ ",W^ , W

, WJ ",

and W

* for the second butterfly. If a look-up table is used to store the

twiddle factors, a table to store y real constants is required for straightfor-

Summary

161

ward access of all the twiddle factors. The table size can be further reduced

using trigonometric identities to compute some of the twiddle factors. The

access of almost double the number of twiddle factors is a drawback of

this algorithm compared with the 2 x 1 PM DFT algorithms. Therefore,

this algorithm is not recommended when all the twiddle factors are com-

puted. Even when twiddle factors are stored in a table, the reduction in

execution time is not much and it comes only with doubling the size of the

twiddle factor table. Therefore, for software applications, this algorithm

is not of much advantage. The butterfly of this algorithm requires fewer

number of components and this is an advantage when the whole butterfly

is implemented in hardware, in high speed applications.

7.4 Summary

• In this chapter, the 2 x 2 PM DIT DFT and DIF DFT algorithms

were derived. These algorithms reduce the number of arithmetic

operations by merging the multiplication operations of adjacent

stages.

• The 2x2 PM butterfly is highly suitable for hardware implemen-

tation.

• In the next chapter, we present efficient procedures for the use of

the algorithms for complex data in processing real-valued signals.

References

(1) Sundararajan, D., Ahmad, M. O. and Swamy, M. N. S. (1994)

"Computational Structures for Fast Fourier Transform Analyzers",

U.S. Patent, No. 5,371,696.

(2) Sundararajan, D., Ahmad, M. 0. and Swamy, M. N. S. (1998)

"Vector Computation of the discrete Fourier Transform", IEEE

Trans. Cir. and Sys. II, vol. CAS-45, No.4, pp.

449-461.

Programming Exercise

7.1 Write a 3-butterfly program to implement the 2 x 2 PM DIT DFT

algorithm.

Chapter 8

DFT Algorithms for Real Data - I

We assumed, thus far, that the input data is complex-valued in develop-

ing DFT algorithms. However, signals are real-valued in most practical

applications. There are two methods used to compute the DFT of real

data using the algorithms for complex data. The first method is to use the

algorithms directly. The relatively more efficient second method is to use

the algorithms by packing the real data to form complex data. In Sec. 8.1,

the direct use of an algorithm for complex data is presented. In Sec. 8.2,

the computation of DFTs of two real data sets at a time is presented. In

Sec.

8.3, the computation of the DFT of a single real data set is described.

8.1 The Direct Use of an Algorithm for Complex Data

The algorithms for complex data can be used for real data by converting the

real numbers into complex numbers with the value of the imaginary parts

zero.

Although this approach requires about double the memory and the

processing compared with more efficient approaches, we recommend this

if the speed and storage requirements are not critical as it is the simplest

approach.

In order to understand the more efficient algorithms for real data, we

have to look at the trace tables of algorithms. Figure 8.1 shows the trace

of the 2 x 1 PM DIT DFT algorithm for real input data with N = 32.

Figure 8.2 shows the trace of the 2 x 1 PM DIF IDFT algorithm for the

transform of real data, shown in Fig. 8.1. The first column values, in

Fig. 8.1, are 32 real input values. The result of vector formation and swap-

ping is shown in column two. The third, fourth, fifth, and sixth column

163