Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

164

DFT Algorithms for Real Data - I

x(0)

x(16)

a:(l)

*(17)

x{2)

x(18)

x(3)

x(19)

x(4)

z(20)

ar(5)

x(21)

ar(6)

x(22)

x(7)

ar(23)

*(8)

z(24)

x(9)

ar(25)

ar(10)

a: (26)

x(ll)

z(27)

x(12)

a: (28)

x(13)

x (29)

ar(14)

ar(30)

ar(15)

x(31)

9h-8

8-6

21-5

8|-3

4-31

6-3

20 +

j'O

0 + jO

-8 + J4

-8-j4

19 +

7 + jO

5 +

5-j6

J6-15

15+jO

-11+jO

2+j5

2-j5

15 + jO-11.00-jll.OC

ll+j0-11.00+jll.0c|-15.

-3 + jO

22+jO

12+jO

-1+jS

-1-J3

12 + jO

0+jO

2+j6

2-j6

18 + jO

8+jO

-3-

-3 +

J3I

18 + jO

4 + jO

3-j7

3 + j7

39.00 +

jO.OO

1.00 + jO.OO

-0.22 + J4.71

-15.78+ J3.29

0.00-J7.00-15

0.00 + J7.00

.78-

-0.22

•

•J3.

•

j4.71

2S-16

30.00

4-jO.OO

0.00 + jO.OO

-0.12 + J7.12

4.12 + j2.

-14.70 -.71.62

.86 + J8.20 88-16

4.12-J2.88

-0.12-j7.12

34.00 + jO.OO

10.00 + jO.OO

4.66 + J5.83

-6.66 + J0.17

12.00 + jO.OO

12.00+ JO.O0

-6.66-jO.

4.66 - J5.83

36.00 + JO.O0

0.00 + jO.OO

j"3-5

83 -j 10.07

0.17 + j4.07

8.00 -

j'4.00

8.00 + J4.00

-0.17-j4.07

-5.83 + J10.07

69.00 + jO.OC

9.00 + jO.OO

2.39 + J11.33

-2.83 -

j'1.92

.56 - J7.0C

15.56 - J7.00

.86 - J8.2C

14.70 + J1.62

1.00 + jO.OO

15.56+ J7.0C

56 + j7.00

-2.83 + J1.92

2.39-J11.33

70.00 + jO.OO

-2.00 + jO.OO

-4.58-jl.25

13.90 + J12.9C

14.83

9.17

-J8.4S

j"8.49

1-10.48

-2.83

- jl.57

+ J1.23

10.00

+ jO.OC

jO.OO

-2.83

h 10.48

j'1.23

+ J1.57

9.17

14.83

- J8.49

j'8.49

13.90 -

-4.58

-J12.90

+ J1.25

139+jO.OO

-1.00+jO.OO

-2.35+j'll.Ol

7.13+J11.66

-5.10-j20.51

-26.01+j"6.51

-26.45 -

j'3.68

-7.27-jl2.72

8.07 -

j"7.07

-6.07 +

j'7.07

-17.29+

j'0.05

-12.10-j'3.29

11.23-j'4.72

19.89+ j 18.72

-12.78-j 14.23

7.11+J18.06

9.00 + J2.00

9.00 -

j'2.00

7.11-j

18.06

-12.78+j"14.23

19.89-j 18.72

11.23+J4.72

-12.10+J3.29

-17.29-jO.05

-6.07 - J7.07

8.07 + j7.07

-7.27 + J12.72

-26.45+ J3.68

-26.01-j'6.51

-5.10 + J20.51

7.13-J11.66

-2.35-jll.01

X(0)

X(16)

X(l)

X(17)

X(2)

X(18)

X(3)

X(19)

X(4)

X(20)

X(5)

X(21)

X(6)

X(22)

X(7)

X(23)

X(8)

X(24)

X(9)

X(25)

X(10)

X(26)

X(ll)

X(27)

X(12)

X(28)

X(13)

X(29)

X(14)

X(30)

X(15)

X(31)

Fig. 8.1 The trace of the 2x1 PM DIT DFT algorithm for real input data, with

= 32,

clearly showing the redundancies.

The Direct Use of an Algorithm for Complex Data

165

138.00 + J0.00

140.00 + J0.00

4.78 + J22.67

-9.48 - jO.65

-31.11 -

j'14.0

20.91 - J27.02

-33.72 -J16.40

-19.18+ J9.04

2.00 + jO.OO

14.14 -jU.14

-29.39 -J3.24

-5.19 + J3.34

31.12+ J14.00

-8.66 -j'23.44

-5.67 + J3.83

-19.89 -J32.2S

18.00 + J0.00

0.00 + J4.00

-5.67-j3.83

19.89 -J32.29

31.12 -j 14.00

8.66 -J23.4A

-29.39 +J3.24

5.19 + J3.34

2.00 + jO.OO

-14.14-jl4.l4

-33.72 +J16.4C

19.18+J9.04

-31.11 + j 14.00

-20.91 -;27.02

4.78 - j'22.67

9.48 - jO.65

156.00 + jO.OO

120.00+ J0.00

-0.89 +j 18.84

10.45 + j'26.50

0.01 - J28.00

-62.23 + jO.OO

-63.11-J13.16

-^.33 -j/19.64

4.00 + jO.OO

0.00 + jO.OO

-63.11+J13.16

4.33 -j 19.64

0.01 + j 28.00

62.23 + jO.OO

-0.89 - J18.84

-10.45+ J26.5

136.00 + jO.OO

144.00 + jO.OO

18.62 + J23.32

-36.96 -j'28.29

48.00 + jO.Ol

11.32 -J33.93

-26.63 -J0.68

-15.31 - J5.60

39.99+ JO.O0

0.00 + jO.OO

-26.63 +J0.68

15.31 -J5.60

48.00 - jO.Ol

-11.32 -J33.93

18.62-J23.32

36.96 - J28.29

160.00 + J0.00

152.00+ J0.00

-64.0 + j'32.00

62.22+ J5.68

0.02+jO.OO

0.00 - j'56.00

-64.0 - J32.00

-£2.22 + j5.68

120.00+ JO.O0

16.00 + J40.00

-16.97+j 16.97

-88.01+ JO.O0

0.00 -j'88.01

16.00 - J40.00

16.97+ J16.97

175.99+ JO.O0

96.01 + JO.O0

-8.01 + J24.0C

45.25 + J22.64

96.00 + JO.O0

O.OO

+ jO.02

-8.01 - j'24.00

-45.25 + J22.64

144.00+ JO.O0

144.00 + JO.O0

-24.00 -J24.00

-22.63 -j'56.57

63.99+ JO.O0

0.00 - J31.98

-24.00+ J24.00

22.63 -

j'56.57

160.02 + jO.OO

159.98 +

jO.OO

-128.0 + JO.O0

0.00 + j'64.00

208.00+ J0.00

96.00 + jO.OO

79.96 + jO.OO

0.00 + J96.03

31.99 + J0.00

208.01 + jO.OO

32.00 + jO.OO

0.00 + J80.00

208.01 + jO.OO

31.99 + JO.O0

-48.00 + jO.OO

0.00 - jO.Ol

271.99+ J0.00

79.99 + jO.OO

-16.02+ J0.00

0.00+j'48.00

95.99 + ;0.00

96.03 + jO.OO

31.97 + J0.00

0.00 + J96.01

207.99 + jO.OO

80.01 + jO.OO

-48.01 + jO.OC

0.00 - J48.0C

175.98 + jO.OO

112.02 + jO.OO

48.00 +

JO.O0

0.00-J112.00

32.02

288.02

255.97

288.02

64.00

-0.01

159.98

256.00

287.96

128.04

127.96

64.01

160.01

256.01

223.98

127.99

95.98

223.98

31.99

127.99

128.01

288.00

128.00

32.01

-0.03

192.03

0.02

192.04

32.01

31.98

224.03

0.00

Fig. 8.2 The trace of the 2 x 1 PM DIF IDFT algorithm for the transform of real data,

with N = 32, clearly showing the redundancies.

166

DFT Algorithms for Real Data - I

vectors are obtained after the first, second, third, and fourth stage opera-

tions of the algorithm are carried out. The redundancies are evident. The

imaginary parts of the input are all zero. Duplication of values exists in

various stages of the algorithm. For example, the second half of the output

is redundant and, therefore, we need not compute and store these values.

In Fig. 8.2, the result of vector formation is shown in column one. The

second, third, fourth, and fifth column vectors are obtained after the first,

second, third, and fourth stage (including swapping of output vectors) op-

erations of the algorithm are carried out. The output values have to be

divided by the length, N = 32, to get back the input values shown in

Fig. 8.1. Note that the output values are not precise. For example, the

first value is 32.02 instead of 32 because we input the DFT values with

only a precision of 2 digits after the decimal point. The second half of

the input vectors is redundant. The output of the various stages exhibits

symmetry. The imaginary parts of the output values are zero.

The redundancies can be eliminated by: (i) packing the real data to

form complex data or (ii) cutting out the redundancies in each stage of the

algorithm. The first approach is described in this chapter and the second

approach is presented in the next chapter.

8.2 Computation of the DFTs of Two Real Data Sets at a

Time

In this method of computing the DFT of real data (RDFT), we compute

the DFTs of two real data sets using a DFT algorithm for complex data

for the same data length, thereby removing the factor of two redundancy

in computation and storage. One set of real input data is stored in the real

part of the complex input data and the other set is stored in the imaginary

part. The DFT is computed and then the individual DFTs of the two sets

are separated by using the linearity property of the DFT and the fact that

the DFT of a real data set is hermitian-symmetric.

Let x(n) and y(n) be the data sets, each with N real values. Let X(k)

and Y(k) be their respective DFTs. Due to the linearity theorem,

c(n) = x(n) + jy(n) & X{k) + jY{k) = C{k)

Since x(n) and y(n) are real sequences, due to the hermitian-symmetric

Computation of the DFTs of Two Real Data Sets at a Time

167

(start}

Read x(n),y(n),

n =

0,1,...,

—

Form c(n) = x(n)

jy{n), n =

0,1,...,

—

Compute C(k) = DFT(c(n))

X(0) = Re(C(0)),X(£)

Re(C(f))

Y(0)

Im(C(0)),Y(f)

Im(C(f))

X(k) =

Compute

C(k)+C*(N-k) y^ _ C(k)-C'(N-k)

1,2,..

•

, 2

-1

Write JST(fc),y(fc),

0,1,...,

( Return)

Fig. 8.3

The

flow

chart of the algorithm to compute two RDFTs, each of length

the same time using a DFT algorithm for the same data length.

property, X{N-k) = X*{k) and

Y{N -

k) = Y*(k). Therefore,

C(N-k) = X*(k)+jY*(k)

Conjugating both sides, we get

C*(N-k)=X(k)-jY(k)

Solving for

X(k)

and Y{k), with C{k) = X(k)+jY(k), we get

X(k)

C{k)+C^N-k)

Yft)

g(fc)-C"CAr-fc)

(8.1)

The flow chart of the algorithm to compute RDFT, for an even

is shown

in Fig. 8.3. Only half of the DFT values are computed since each DFT

hermitian-symmetric.

168

DFT Algorithms for Real Data - I

(start)

Read X(k), Y(k), k =

0,1,...,

C(0) = X(0)+jY(0),C(f) = X(f) + jY(£)

Form C(k) = X{k) + jY(k),

C(N -k) = X*(k) + jY* (k), k =

1,2,...,

f - 1

Compute c(n) = IDFT(C(fc))

Form x(n) = Re(c(n)),

j/(n)

= Im(c(n)), n =

0,1,...,

iV - 1

Write x(n),y(n), n =

0,l,...,N

-1

TReturnJ

Fig. 8.4 The flow chart of the algorithm to compute two RIDFTs, each of length N, at

the same time using an IDFT algorithm for the same data length.

The flow chart of the algorithm to compute RIDFT, for an even N, is

shown in Fig. 8.4. Only half of the DFT values are input since the DFTs

are hermitian-symmetric. Flow charts in Figs. 8.3 and 8.4 can be modified

for an odd N.

Example 8.1 Find the DFT of the sequences x{n) — {2,3,4,2} and

y{n) =

{3,1,1,2}.

Compute x(n) and y(n) back from the DFT values.

Solution

Form the complex values c(n) = x(n)+jy(n) — {2+jS,3+jl,4+jl,2+j2}.

The DFT of c{n) is C{k) = {11 + P, -3 + jl,

+ jl, -1 +

;3}.

To separate X(k) and Y(k), we use Eq. (8.1).

X(0)

X(l)

X(2)

X(3)

Re(C(0))

(-3+jlH(-l-J3)

Re(C(2))

X*(l)

-2-jl

-2+jl

Computation of the DFT of a Single Real Data Set 169

Y(0) = Im(C(0)) = 7

y(i) = (-3+ii)-(-i-J3)

= 2 + jl

y(2) = Im(C(2)) = 1

y(3) = y*(i) = 2-ji

To compute the RIDFT, X(fc)+.7 Y(fc) is formed and the IDFT is computed.

The result gives x(n) as the real part and y(n) as the imaginary part. For

this example, X{k)+jY(k) = {11+j7,-3+jl,l+jl,-l+j3}. The IDFT

of this sequence yields x(n) + jy(n) = {2 + j3,3 + jl, 4 + jl, 2 +

j2}.

The number of real additions required to separate the two DFTs is

—

4. Therefore, for computing an JV-point RDFT, the number of op-

erations required is N

—

2 more than one-half of that of the algorithm for

complex data used.

8.3 Computation of the DFT of a Single Real Data Set

In this method of computing the RDFT, the redundancy is removed by: (i)

computing the DFTs of even and odd indexed input values using a single

DFT algorithm for half data length rather than two, as in the case of the

algorithm for complex data with zero imaginary parts and (ii) computing

only half of the DFT values in combining the two smaller DFTs.

Let x(n) be the data set with N real values whose DFT, X(k), is to be

computed. Leta;(

)(n) = x(2n) anda;(°)(n) = x(2n + l),n =

0,1,...,

-1.

Let X<

)(fc) and X^ik) be their respective DFTs. Then,

(e)

(n) + jx^ (n) o X^ (k) + jXM (k)

As described in the last section, X^(k) and X^(k) can be computed using

a single DFT algorithm for data length —. The DFTs can be combined

to get X(k) = X^(k) + W#X(°)(fc). The flow chart of the algorithm

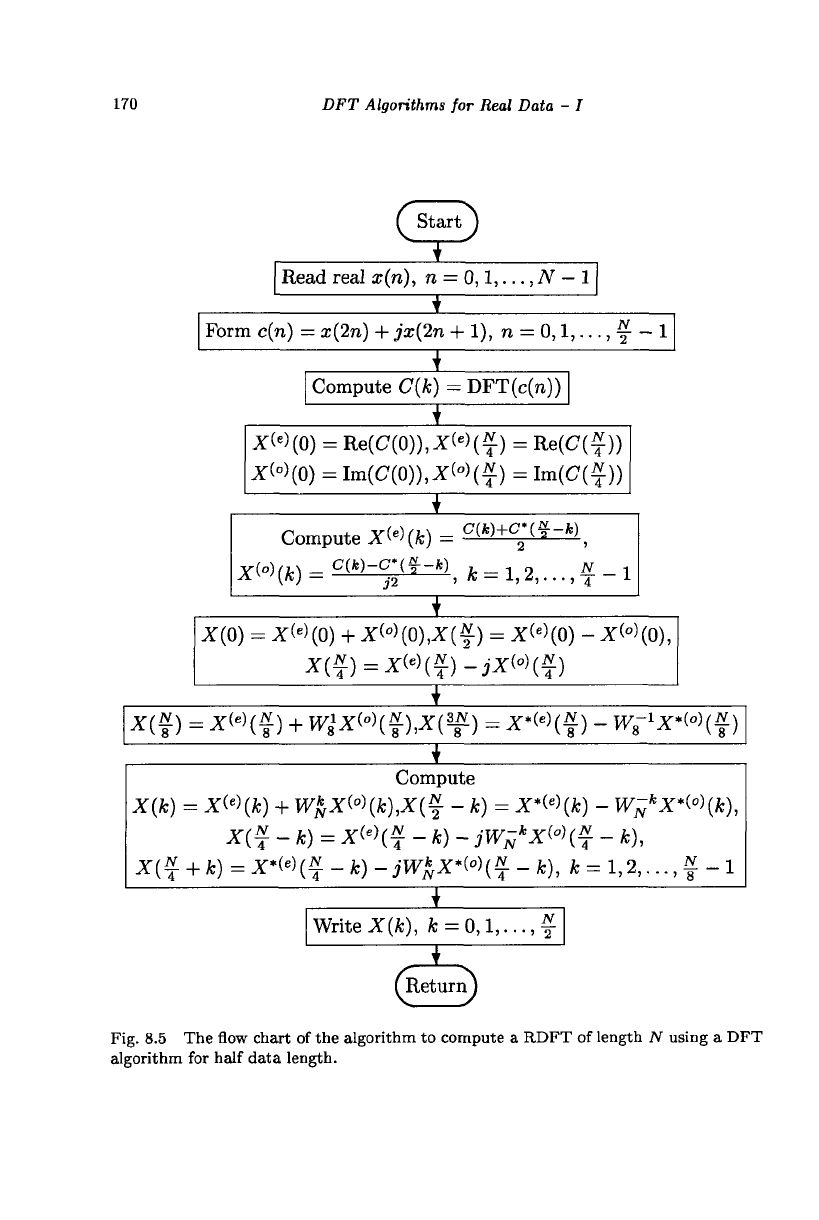
to compute RDFT, for N an integral multiple of 8, is shown in Fig. 8.5.

It can be modified for any even N. This flow chart shows how we can

implement this algorithm with minimum arithmetic operations and twiddle

factor access. Note that, in merging the DFTs of the even and odd indexed

data, only half the number of multiplications shown in Fig. 8.5 are actually

required.

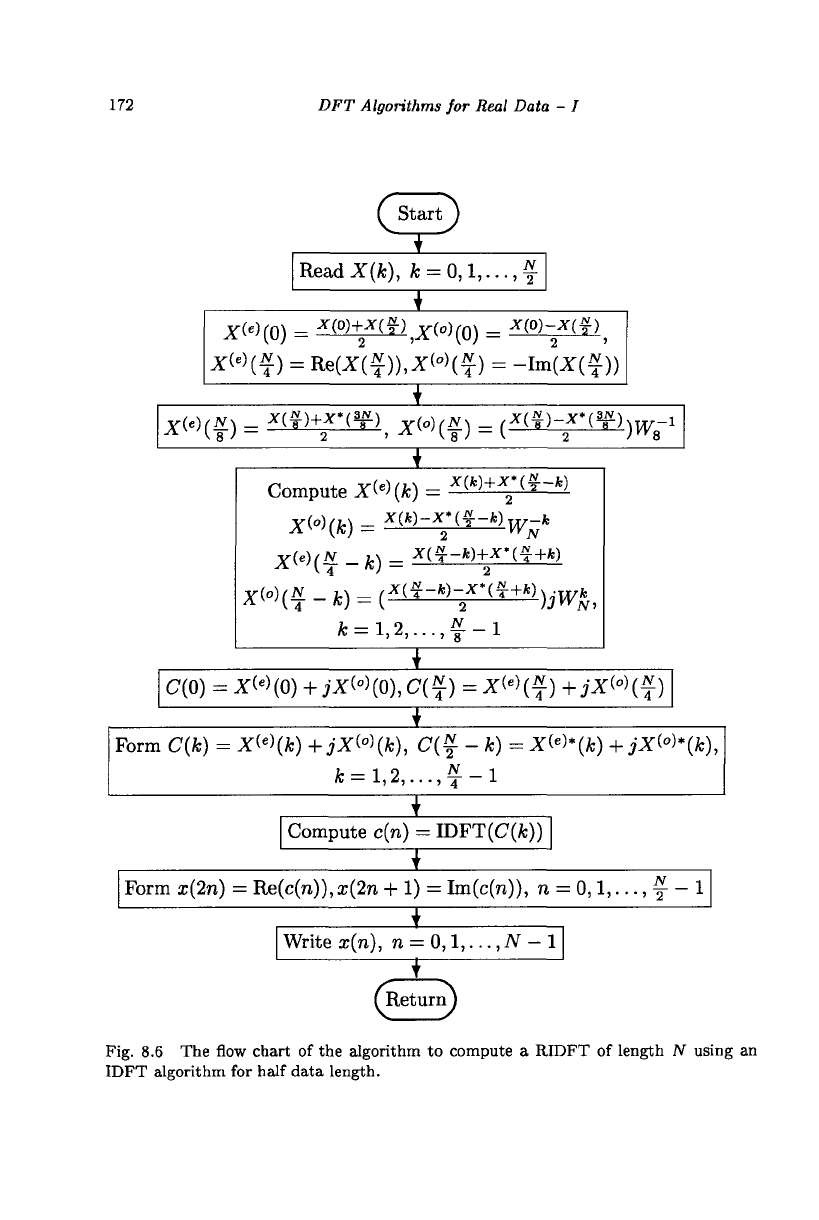
In computing the RIDFT, the redundancy is removed by: (i) computing

only half of the input values for the two independent IDFTs computing the

170

DFT Algorithms for Real Data - I

(start)

^r^

Read real x(n), n = 0,1,...,N

—

•

Form c(n) = x(2n) + jx(2n + 1), n =

0,1,...,

^ - 1

Compute C{k) = DFT (c(n))

XW(0) = Re(C(0)),XW(f) = Re(C(f))

XW(Q) = Im(C(0)),X(°)(g) = Im(C(f))

Compute xM(fc) =

;^-*>,

(

)

(fc)

g(fc)-^(f-fc)

! fc==

,...,f -1

X(0) = lW(0) + X(°)(0),X(f) = X«(0) - X(°)(0),

X(f) = X(°)(f)-jX(°)(f)

(f) = xW(f)

+ w£x(°)(%),x(

-£)

= x*^(f) - Wf

*^*)

X(fc)

X(£

= XW(ifc)

*(£

+ fc) = X'

+ w#x(°)

-*) =

{ 4

-*)

Compute

(fc),X(f-

>(?-*)-

- jW#X*

-*) =

-m

v 4

x*w

-k),

(*)"

-W^

-fc),

1,2,.

fe^*(o)

••

(*),

-1

Write X(k), k =

0,l,...,f

(Return)

Fig. 8.5 The flow chart of the algorithm to compute a RDFT of length N using a DFT

algorithm for half data length.

Computation of the DFT of a Single Real Data Set

171

even and odd indexed data values and (ii) computing the two IDFTs in a

single IDFT algorithm for half data length, as described in the last section.

Given X(k), we have

X{k) = X(

\k) + WJt,X(°\k)

X{j + k) = XM(k)-Wkx(°\k)

Since the DFT of real data is hermitian-symmetric, the last equation can

be written as

x*(^ -k)

xW(fc) - wkx(°\k)

Solving for xM(fc) and X(°)(fc), we get

*•>(*, = *""+*•<?-*> (8.2)

xMm =

(iw-rff-w^

0jl

(g3)

The IDFT of C(k) = (XW(fe) + jX^(k)) is c{n) = {x^{n) + jx^(n)).

The flow chart of the algorithm to compute RIDFT, for N an integral

multiple of 8, is shown in Fig. 8.6. It can be modified for any even A

Example 8.2 Find the DFT of the sequence x(n) = {2,3,3,1,4,1,2,2}.

Compute x{n) back from the DFT values.

Solution

Form the complex data c(n) = x^

(n)

+ jy^ (n) = {2 + j3,3 + jl,

jl,2

j2}. The DFT of

c{n)

is C(fc) =

{11

+j7,-3 +jl,l +jl,-l +j3}.

To separate X{k) and Y(k), we use Eq. (8.1). XW(0) = ll,XW(l) =

-2-jl,XW(2) =

1,XW(3)

= -2 + jl and Jf(°)(0) = 7,X<°>(1) = 2 +

jl, Jf (°)(2) =

X(°)(3) =

- jl. Combining the two DFTs, we get

X{0) =

+ 7 = 18

X(l) =

-jl)

+ -L(l-jl)(2+jl) = 0.12-J1.71

X(2) = l-ji

X(3) = (-2 + jl)-i(l+jl)(2-jl) = -4.12 + J0.29

X(4) = 11-7 = 4

X{5) = X*(3) = -4.12-j0.29

X(6) = X*(2) = 1+jl

X(7) = X*(l) = 0.12 + J1.71

172 DFT Algorithms

for

Real Data

- I

(start)

ReadX(fc),

fc =

0,l,...,f

(e)

(0)

X(0)

X(f)

)X(o)(0)

X(0)-X(f)

;

XW(f)

Re(X(f )),X(°)(f)

-Im(X(f))

XW(f)

*(*>+**(¥>,

*(.)(*)

(

*(*

)-**(^jwr-i

Compute X«(re)

*(*)+**(*-*)

x(«)(fc)

*(*)-**(*-*)

jy-*

)(^

- fc) =

^(f-

(f+fe)

XW(f

-'fc) = [

+k)

)jW*

1,2,...,

-g 1

C*(0)

= XU

(0)

jX(°)

(0),

=JrW(f)+

^W(f)

Form

C(k) =

X^(k)

+jX<-°\k),

1,2,

<?(f

Jfe)

XW*(re)

jX(°)*(re),

Compute

c(n)

= IDFT(C(ifc))

Form

x(2n) =

Re(c(n)),x{2n +

= Im(c(n)),

n =

0,l,...,f-1

Write

x(n),

0,1,...,

- 1

( Return)

Fig.

8.6 The

flow chart

the

algorithm

compute

RIDFT

length

using

IDFT algorithm

for

half data length.

Summary

173

Note that

the

products ^-(1

jl)(2

jl)

and ^(1

jl)(2

- jl)

are

complex conjugates.

To compute the RIDFT, we use Eqs. (8.2) and (8.3),

get

X^(k)

and

XM(k)fromX(k).

)(0)

= iMi =11

)(l)

(0.12-jl.71)+(-4.12-j0.29)

_ _2 - jl

XW(2)

Re(i(f))

= 1

lW(3)

\l)

= -2

X(°)(0)

= ±t! =7

X(°)(l)

= (0-H-Jl-71?-(-4.12-j0.29)^

(1+jl) =

XW(2)

-Im(X(f))

= 1

XW(3)

X*(°)(l)

= 2-jl

X^(k)

+jX^(k)

formed and the IDFT

computed. The result gives

(n) as the real part and

(n) as the imaginary part. For this example,

X^ (k)+jX(°\k)

{11+ J7,-3+jl,l+jl,-l+j3}

The IDFT

this sequence yields c(n)

(n) +

jx^

(n)

j3,3

jl,4 + jl,2+j2).

The additional operations required to compute an TV-point RDFT, apart

from that of

^--point DFT algorithm for complex data, are as follows.

separate the DFTs

X^(k)

and

X^(k),

TV —

4 real additions are required.

The number of real multiplications needed is TV-6. The number of addition

operations due to complex multiplications is

—

The number of addition

operations required

combine X(

\k) and X(°)(fc)

TV —

2. Therefore,

the additional operations required

—

multiplications

and

—

additions.

8.4 Summary

•

this chapter, two methods were presented

for

the computation

of the RDFT and the RIDFT.

•

the speed and storage requirements are not critical, the real data

can be assumed

be complex data with zero imaginary parts and

algorithms for complex data can be used directly.