Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

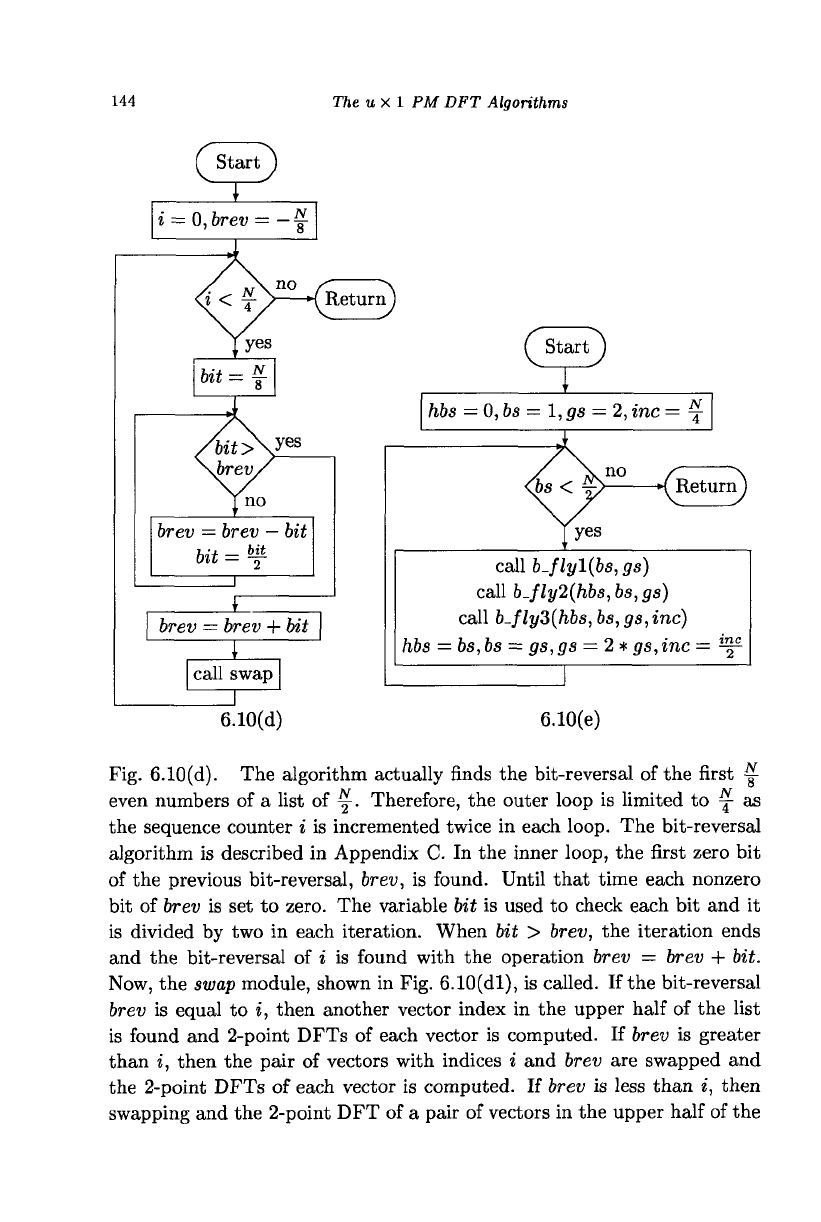
144

The uxl PM DFT Algorithms

(Return J

brev = brev + bit

call swap

hbs -

f Start")

= 0, bs = 1,5s = 2, inc =

' 4

( Return j

call b-flyl(bs,gs)

call b_fly2(hbs, bs, gs)

call b-fly3(hbs, bs, gs, inc)

hbs = bs,bs

—

gs,gs = 2 * gs, inc = ^

6.10(d) 6.10(e)

Fig. 6.10(d). The algorithm actually finds the bit-reversal of the first y

even numbers of a list of y

•

Therefore, the outer loop is limited to j- as

the sequence counter i is incremented twice in each loop. The bit-reversal

algorithm is described in Appendix C. In the inner loop, the first zero bit

of the previous bit-reversal, brev, is found. Until that time each nonzero

bit of brev is set to zero. The variable bit is used to check each bit and it

is divided by two in each iteration. When bit > brev, the iteration ends

and the bit-reversal of i is found with the operation brev = brev + bit.

Now, the swap module, shown in Fig. 6.10(dl), is called. If the bit-reversal

brev is equal to i, then another vector index in the upper half of the list

is found and 2-point DFTs of each vector is computed. If brev is greater

than i, then the pair of vectors with indices i and brev are swapped and

the 2-point DFTs of each vector is computed. If brev is less than i, then

swapping and the 2-point DFT of a pair of vectors in the upper half of the

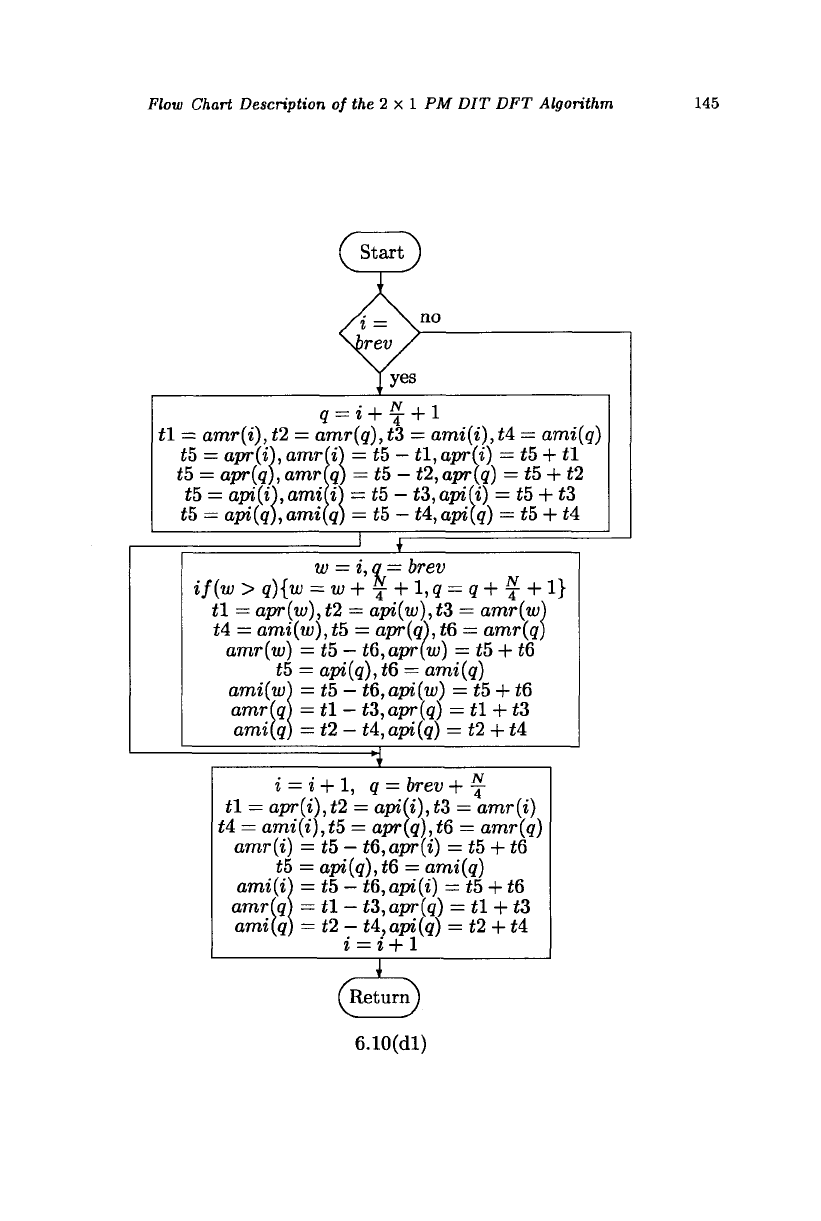
Flow Chart Description of the 2 x 1 PM DIT DFT Algorithm 145

f Start J

£1 = amrii), t2 = amriq),

£3

= ami(i),

£4

= amiiq)

£5 = aprii), amrii) = £5

—

tl,aprii) = £5 + tl

£5 = apriq), amriq) = £5 - £2,apr(g) = £5 + £2

£5 = apt(t),amm) = £5 - £3,api(t) = £5 + £3

' " " •'- £5+ £4

t5 = api(i),omim = £5

—

£3,api(t)

£5 = api(q),ami(q) = £5

—

£4,api(g)

u; = i, q

—

brev

ifiw > q){w = w+% + l,q = q+% + l}

tl = apr(tu),t2 = api(u;),£3 = amr(tu

£4 = ami(w),£5 = apr(g),£6 = amriq

amriw) = £5

—

£6,apr(w) = £5 + £6

£5 = apiiq),

= amiiq)

amiiw) = £5

—

£6,api(u;) = £5 + £6

amrfg) =

£1 —

t3,apriq) =

£1

+ £3

omi(g) = £2 -

£4,

apiiq) = £2 + £4

i = i + 1,

= 6rew 4- ^

£1 = ap7-(i),t2 = api(i),t3 = amr(j)

£4 = amz(i),£5 = apr(</),£6 = amriq)

amrii) = £5

—

£6,ajw(z) = £5 + £6

£5 = api(g),£6 = amiiq)

amiii) = £5

—

£6,api(i) = £5 + £6

amriq)

—

£1

—

£3,apr(g) = tl + t3

ami\q) = t2

—

tA, apiiq) = £2 + £4

i = i + l

( Return)

6.10(dl)

146 The u x 1 PM DFT Algorithms

list is carried out. In all the iterations, the vector whose index is the next

higher odd number and the vector whose index is the bit-reversal of the

odd number are swapped and 2-point DFTs computed.

Figure 6.10(e) shows the dit21Sl module. The term dit21 indicates

that the algorithm is the 2 x 1 PM DIT DFT algorithm. This is a three-

butterfly implementation, which is indicated by the number 3. The last

digit 1 indicates that each stage is implemented separately. Two general

and two special types of butterflies are used as presented in Section 6.2.

This flow chart should be followed with the SFG shown in Fig. 6.2. The

variable bs represents the span of a butterfly. The variable gs represents

the span of a group of butterflies. The variable hbs is equal to ^- Variable

inc represents the difference between two indices of the twiddle factors in

the look-up table for a particular stage. These variables are initialized for

first stage values. The loop steps through various stages. The butterfly

span in the last stage of the algorithm is maximum at ^, and therefore,

the value ^-

1S use

d to end the iteration. As the first butterfly in each group

is a special one, module b-flyl is invoked to process this type. This module

processes all the butterfly of this type in a loop as shown in Fig. 6.10(el).

The second special butterfly is required from Stage 2 onwards. The module,

b-fly2, is invoked and it processes all the butterflies of this type in a loop

as shown in Fig. 6.10(e2).

Two general type butterflies are used in the module called b-fly3, shown

in Fig. 6.10(e3). Unlike in the previous cases, the number of butterflies

in each group is more than one. Therefore, two loops are required for

implementation. Two butterflies of the general type are processed at the

same time. This reduces the fetching of the twiddle factors as the twiddle

factors are related in a trivial manner. For each pair of butterflies in the

first group, the indices of the nodes and the twiddle factors are set. The

inner loop steps through all the butterflies with the same twiddle factors in

all groups. The outer loop steps through each butterfly of the first group.

The values are updated and the iteration continues until all the butterflies

in a stage are processed. The ouLput module is shown in Fig. 6.10(f). In

each iteration of the first loop, a pair of values apr(i) and api(i) are printed.

In the second loop, a pair of values amr(i) and ami(i) are printed.

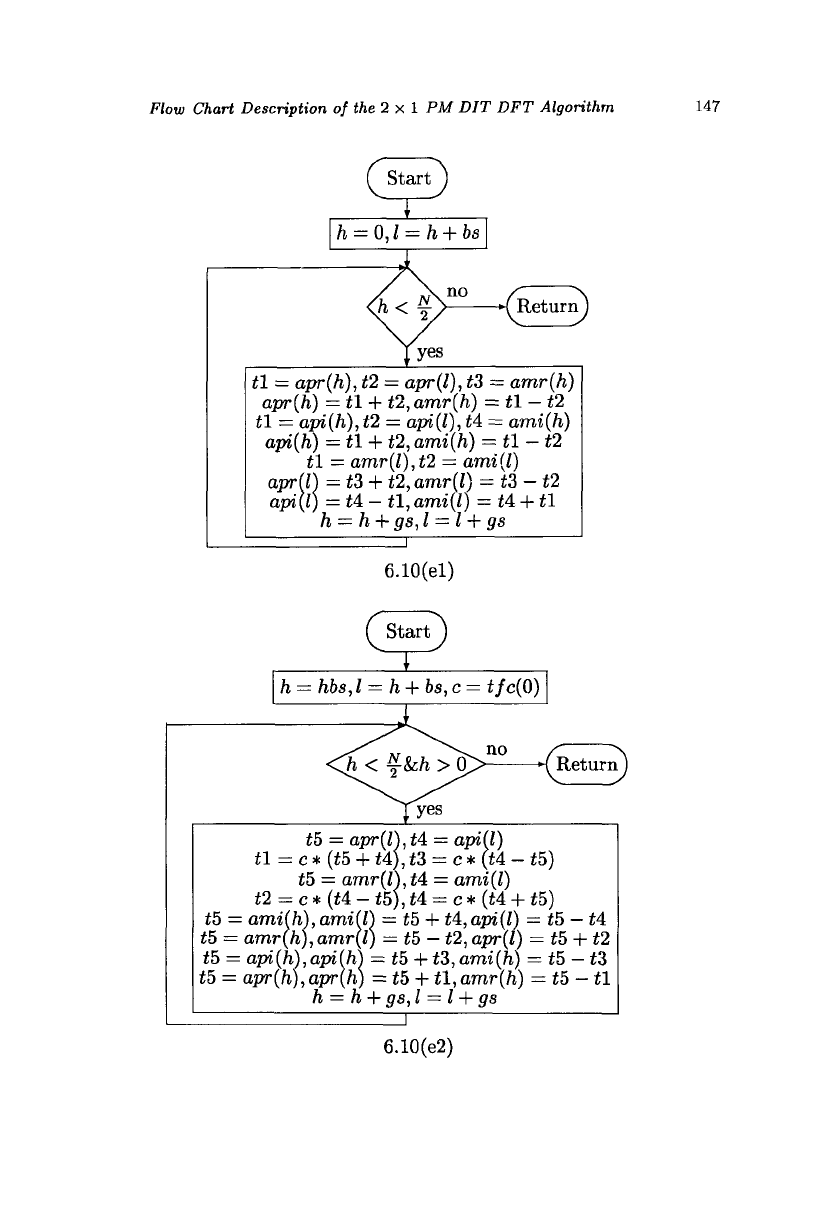
Flow Chart Description of t/ie 2 x 1 PM DIT DFT Algorithm

Start

(Return)

£1 = apr(h),t2 = apr(l),t3 = amr(h)

apr(h) =

£1

+ t2,amr(h) =tl-t2

£1

—

api(h),t2 = api(l),H = ami(h)

api(h) =

£1

£2,

ami(h) = tl-t2

£1 = amr(l),t2 = ami

(I)

apr(l) = £3 + t2,amr(l) = £3 - £2

api(l) = £4 - tl,ami(l) = £4 + £1

ft = ft + gs,

+ gs

6.10(el)

f Start")

ft = hbs,

= h + bs,c = £/c(0)

(Return)

£5 = apr(Z),£4 = apiVt)

£1 = c

(£5 +

£4),

£3

= c

(£4 - 45)

£5 = amr(l),H = ami(l)

t2 = c

(£4 -

£5),

£4

= c

* (£4

+ £5)

£5 + £4,api(J) = £5-£4

£5 = amr(h),amr(l) = £5

—

£2,

apr(Z) = £5 + £2

£5 = api(h), api(h) = £5 +

£3,

ami(h) = £5

—

£3

£5 = apr(h),apr(h) = £5 + £l,amr(ft) = £5 - £1

ft = ft +

<7S,

/ = I + gs

6.10(e2)

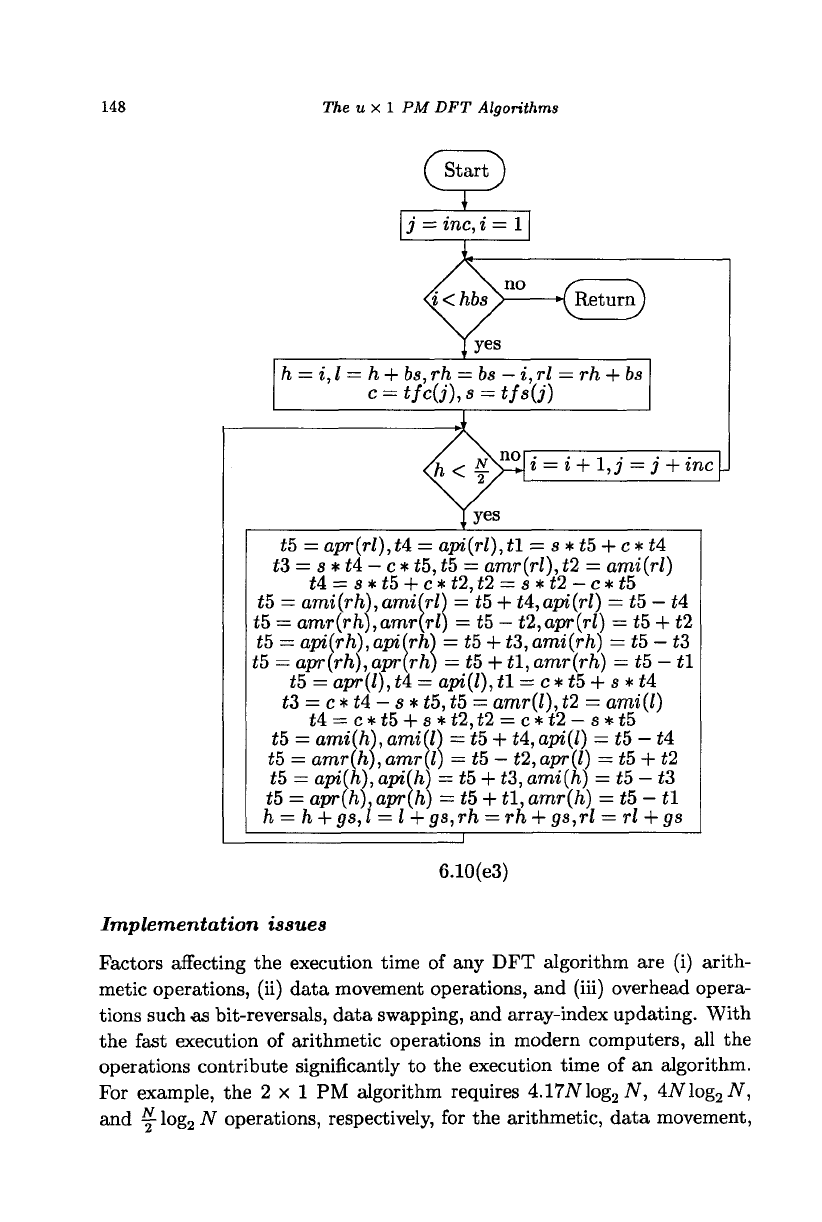
148

The u x 1 PM DFT Algorithms

(Return)

h = i,l = h + bs,rh = bs

—

i, rl

—

rh + bs

c = tfc(J), s = tfs(j)

,.\UU • • , -i • . -

£5 = apr(rl),t4 = api(rl),tl = s * £5 + c* £4

£3 = s * £4

—

£5,

£5

= amr(rZ),£2 = ami(rl)

tA = s * £5 +

£2,

£2

= s * £2

—

c * £5

£5 = ami(rh),ami(rl) = £5 + £4,api(r/) = £5

—

£4

£5 = amr^r/i^amr^rZ) = £5

—

t2,apr(rl) = £5 + £2

£5 = api(rh),

apiOrh)

= £5 +

£3,

ami(rh) = £5

—

£3

£5 = apr(rh), apr{rh) = £5 +

£1,

amr(rh) = £5

—

£1

£5 = apr(Z), £4 = api(l),

£1

= c

£5 + s * £4

£3 = c

£4 - s *

£5,

£5

= amr{l),

£2

= ami(l)

£4 =

£5

+ s *

£2,

£2

£2 — s

* £5

£5 = ami(h), ami

(I) —

£5 +

£4,

api(Z) = £5 - £4

£5 = omr(/i),omr(I) = £5

—

£2,opr(Z) = £5 + £2

£5 = api(h), api(h) = £5 +

£3,

ami(h) = £5

—

£3

£5 = opr(ft), apr(/i) = £5 +

£1,

amr{h) = £5

—

£1

h = h + gs,l = I + gs,rh = rh + gs, rl = rl + gs

6.10(e3)

Implementation issues

Factors affecting the execution time of any DFT algorithm are (i) arith-

metic operations, (ii) data movement operations, and (iii) overhead opera-

tions such as bit-reversals, data swapping, and array-index updating. With

the fast execution of arithmetic operations in modern computers, all the

operations contribute significantly to the execution time of an algorithm.

For example, the 2 x 1 PM algorithm requires 4.17iVlog

N, 4JVlog

./V,

and y log

N operations, respectively, for the arithmetic, data movement,

Summary

149

and the array-index updating for large values of N. The last two operation

counts can be reduced by a factor of two by implementing the operations of

two consecutive stages together. This involves executing four 2x1 PM but-

terflies, two from each stage of a pair of adjacent stages, at the same time.

Modern arithmetic units typically have 16 or more registers. Single-stage

implementation of a 2 x 1 PM algorithm requires 7 registers whereas two-

stage implementation requires about twice as many registers. Therefore,

implementing pairs of consecutive stages concurrently results in efficient

The process of implementing the operations of two consecutive stages at a

time is almost a mandatory requirement in order to achieve a fast execution

on modern processors, since the execution is very fast once the operands

are in the registers.

In conclusion, for good performance of the algorithms, the requirements

are the availability of: (i) sufficient number of registers, (ii) a plus-minus

instruction, (iii) a multiply-add instruction, and (iv) efficient generator for

twiddle factors. Further speedup can be achieved by using one or more

hardware butterflies, or parallel processors.

6.10 Summary

• Fast DFT algorithms essentially spread the computation over sev-

eral stages, develop partial results in each stage, and use them in

an optimum way to compute all the N frequency coefficients.

• In this chapter, the u x 1 PM DFT algorithms were presented.

The algorithms are an interconnected network of butterflies, each

butterfly representing a set of operations. The particular case with

vector length two was described in detail. DFT algorithms with

vector length two are highly recommended for practical use as they

are simple, regular, and very efficient.

References

(1) Sundararajan, D., Ahmad, M. 0. and Swamy, M. N. S. (1994)

"Computational Structures for Fast Fourier Transform Analyzers",

U.S. Patent, No. 5,371,696.

150

The u x 1 PM DFT Algorithms

(2) Sundararajan, D., Ahmad, M. O. and Swamy, M. N. S. (1998)

"Vector Computation of the discrete Fourier Transform", IEEE

Trans. Cir. and Sys. II, vol. CAS-45, No.4, pp.

449-461.

Exercises

6.1 Derive the 2 x 1 PM DIT DFT algorithm directly from the definition,

with N = 16.

6.2 Derive the 2 x 1 PM DIF DFT algorithm directly from the definition,

with

= 16.

6.3 Derive the 6 x 1 PM DIT DFT algorithm directly from the definition,

with N = 48.

Programming Exercises

6.1 Write a 3-butterfly program to implement the 2 x 1 PM DIT DFT

algorithm.

6.2 Write a two stages at a time 3-butterfly program to implement the 2x1

PM DIT DFT algorithm.

6.3 Write a program to compute a single DFT coefficient using the 2x1

PM DIT DFT algorithm.

6.4 Write a 3-butterfly program to implement the 6 x 1 PM DIT DFT

algorithm.

Chapter 7

The 2x2 PM DFT Algorithms

In this chapter, we describe the 2 x 2 PM DFT algorithms, which reduce the

number of arithmetic operations further compared with the 2x1 PM DFT

algorithms. The reduction is brought about by merging the multiplication

operations of pairs of adjacent stages. The 2x2 PM DIT DFT algorithm

is derived in Sec. 7.1. The 2 x 2 PM DIF DFT algorithm is described in

Sec.

7.2. In Sec. 7.3, the computational complexity of the algorithms is

presented.

7.1 The 2x2 PM DIT DFT Algorithm

Before we derive the 2x2 PM DIT algorithm, however, it is instructive

to find how the number of multiplications are reduced through a careful

examination of the SFG of the 2 x 1 PM DIT DFT algorithm (Fig. 6.2). It

can be observed that, for any stage (except the first one), half of the vector

output values from the previous stage are multiplied in the current stage

by twiddle factors of the form Wfr and W^

+ T

. Instead of carrying out

the two multiplications in the current stage, if we premultiply the two data

values that produce an output vector in the previous stage by Wjy, then no

multiplications would be required in the current stage. A multiplication by

Wj§ is still required, but it is trivial. The twiddle factor W^ shifted from

the current stage is combined with the twiddle factor of the previous stage

for one of the data values, whereas Wjy itself becomes the twiddle factor

for the other data value, since there is no twiddle factor associated with

this data value. Therefore, for every two multiplications eliminated in the

current stage one multiplication is added in the previous stage.

151

152 The

2x2 PM DFT

Algorithms

The combining

the DFTs

two sets

vectors, each

of ^

vectors,

to produce

the

DFT

of a set of

% vectors

in the

last stage

the

2x1 PM

DIT

DFT

algorithm

given

Eqs.

(6.3) and

(6.4), with

u = 2, as

(k)

= Ai

{k) + WZWk4°\k) (7.1)

(k+j)

\k)

WZWlWkA[°\k),

(7.2)

where

k =

0,1,...,^

—

1 and p = 0,1. To

obtain

the

first

and the

third quarter values

(k),

Eqs. (7.1) and (7.2) can be

used with

k =

0,1,...,

—

1. The

second

and the

fourth quarter values

of A

(k) can

be obtained

replacing

with

k + y in

these equations.

The

resulting

equations

are

given

+ ^) = 4°\k+j) + WZW

*Ai°\k + j) (7.3)

(k+*£)

\k+j)

W>W}W

*A{°\k

+ j), (7.4)

where

0,1,...,

—

1. The

quantities

on the

right side

Eqs.

(7.1)

through

(7.4)

represent

the

output values

of the

previous stage. These

values

can be

obtained recursively

4*)(fc)

= AM(k) + W$W™4

°\k) (7.5)

Hk+j) = A\

\k) +

W$W}W*

°\k)

(7.6)

°\k)

= 4°

\k) + WiW™4°

(k) (7.7)

°Hk+j) = A[°

\k) + WZWlW™A[°°\k), (7.8)

where

k =

0,1,...,

f -

and

A^(k), A^(k),

\k),

and

\k)

represent

the DFT of the

vectors

a(n)

such that

mod 4)

is 0, 1 ,2 ,

and 3, respectively. The twiddle factors associated with

the

terms

A^'^k),

A[°\k),

(fc

+ f), and A[°\k + f) in

Eqs.

(7.1)

through

(7.4) can be

merged with those

Eqs.

(7.7) and (7.8) as

°\k)

= W

A^\k) +

W*W$A(°

\k)

(7.9)

°Hk

+ j) = W^A[

\k) +

WiWiW

^A{

oo)

(k) (7.10)

The 2x2 PM DIT DFT

Algorithm

153

The 2x2 PM DIT DFT butterfly

The input-output relation of a butterfly of the 2 x 2 PM DIT algorithm can

be deduced from Eqs. (7.1) through (7.6), (7.9), and (7.10) as

r+1

A<[

r+2

(r+2

\hl)

(11)

"(ll)

\h2)

\K2)

"{12)

"(12)

\hl)

\h2)

(«) + WftM<

(/l)

A^(hl)-WlfA^{ll)

A^(hl)

W^A^{11)

(hl)-W

*A[

(ll) A^(hl)-W

^A[

\ll)

W^m

+ WlfA^m

= W°

A%\h2)-W%°A%\l2)

-__»-l-«-

„.3s+W

r+2)

ai)

r+2)

(zi)

r+2)

«2)

{

\12)

W?*AP{h2)

w°

+ W%

+ 8

•A«(B)

(r)

(

;

)

{l2)

. A(r+1) /ln\

^^(wj + ^^CW)

A£

\hl)-A£

\h2)

+1)

(hl)

W^A^

+1)

(h2)

r+1)

(/il)-^|4

r+1)

(^2)

r+1

)(Zl) + 4

r+1

)(Z2)

r+1

)(n)-4

r+1

)(/2)

r+1)

(/l)

+ wJ"4''

+1)

(/2)

r+1)

(n)-^|4

r+1)

(Z2),

(7.11)

where s is an integer whose value depends on the stage of computation r and

the index hi. The 2 x 2 PM DIT DFT butterfly is shown in Fig. 7.1. The

butterfly computes eight 2-point DFTs along with the multiplication of the

input values by appropriate twiddle factors. This butterfly requires 24 real

multiplications, 44 real additions, and, assuming that sufficient number of

registers is available in the processor, 32 data transfer operations between

the memory and the processor. Two special butterflies requiring reduced

computation can be derived from Eq. (7.11) when s = 0 or s = ^. The

first special butterfly requires 4 real multiplications and 36 real additions

while the second requires 20 real multiplications and 44 real additions.