Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications
Подождите немного. Документ загружается.


174
DFT Algorithms for Real Data - I
• The second method involves the indirect use of algorithms for com-
plex data. The first type of algorithm is to compute two RDFTs or
RIDFTs at a time using a single algorithm for complex data for the
same data length. The second type of algorithm is to compute a
single RDFT or RIDFT using a single algorithm for complex data
for half the data length.
• By using appropriate PM algorithms for complex data, efficient
algorithms for real data when the number of samples is not an
integral power of 2 can be realized.
• An alternative, which is described in the next chapter, is to deduce
algorithms specifically suited for real data from the algorithms for
complex data by cutting out the redundancies in each stage.
Reference
(1) Brigham, E. 0. (1988) The Fast Fourier Transform and Its Appli-
cations, Prentice-Hall, New Jersey.
Programming Exercises
8.1 Write a program to compute two iV-point RDFTs at a time using the
Appoint 2 x 1 PM DIT DFT algorithm for complex data.
8.2 Write a program to compute two AT-point RIDFTs at a time using the
Appoint 2 x 1 PM DIT DFT algorithm for complex data.
8.3 Write a program to compute an Af-point RDFT using the ^-point 2x1
PM DIT DFT algorithm for complex data.
8.4 Write a program to compute an AT-point RIDFT using the ^-point
2 x 1 PM DIT DFT algorithm for complex data.

Chapter
9
DFT Algorithms
for
Real Data
- II
In this chapter, we deduce DFT and IDFT algorithms, specifically intended
for real-valued data, from the algorithms for complex-valued data by remov-
ing
the
redundant processing
in
each stage. These algorithms provide
an
alternative
in
computing
the
RDFT
and
RIDFT
to the
indirect
use of al-
gorithms
for
complex data described
in the
last chapter.
In Sec.
9.1,
the
storage scheme
for
real data
and its DFT is
presented.
In Sec. 9.2, the
2
x 1 PM DIT
RDFT algorithm
is
described.
In
Sec.
9.3, the 2 x 1 PM
DIF RIDFT algorithm
is
derived.
In
Sec.
9.4, the 2 x 2 PM DIT
RDFT
algorithm
is
described.
In
Sec. 9.5,
the 2 x 2 PM DIF
RIDFT algorithm
is
derived.
9.1
The
Storage
of
Data
in PM
RDFT
and
RIDFT
Algorithms
Due
to the
hermitian-symmetric property,
the
storage
of the
first half
of
the spectrum
of
real data
is
sufficient.
The
first half
and the
second half
of the real input data can
be
stored, respectively,
in the
locations assigned
for
the
real
and
imaginary parts
of
the complex vectors. (For following
the
derivations presented
in
this chapter,
the
trace tables shown
in
Figs.
8.1
and
8.2
will
be
helpful.) Therefore,
the
storage
of
data
to
compute
the
RDFT
is
given
by
N
N N
a
(n) =
{a(n),a{n
+
—)}
=
{(x(n)
+ x(n +
—),x{n)
-x(n + —)),
(x(n
+
—)
+ x(n +
-r-),x(n
+ —) - x(n +
-j-))},
N
n
= 0,!,...,--! (9.1)
175

176
DFT Algorithms for Real Data - II
A'(0) = {A(OMo(£)} = {(X(0),X(f)),X(f)}
rq
_-
A'(k)
= A(k) = {X(k),X(k+%)}, fc = l,2,...,£-l
{y
-
Z)
The storage of data to compute the RIDFT is given by
B'(0) = {B(0),B(f)}
= {(X(0)+X(f
),X(0)-X(f
)),(2Re(X(f )),2Im(X(£)))} (9.3)
B'(fc) = B(fc) = {(X(k) + X(k + f)), (X(k) - X(k + f))},
where k =
1,2,...,
f - 1.
b'(n) = {b(n),b(n + ^)}
iV AT 37V
= {(x(n),x(n + -)), (x(n + -),x{n +
~^))},
(9.4)
where n =
0,1,...,
^
—
1.
9.2 The 2x1 PM DIT RDFT Algorithm
Algorithm that is suited to real data is obtained by just eliminating half
the number of butterflies in each group of butterflies of every stage of an
algorithm for complex data along with the necessary changes in the storage
of the data values. The combining of the DFTs of two sets of vectors, each
of ^ vectors, to produce the DFT of a set of y vectors in the last stage of
the 2 x 1 PM DIT DFT algorithm is given as
A
p
(k)
= 4
e)
(fc) + (-ir<4
0)
(fe) (9.5)
A
p
(k
+ ^) = A[
e
\k) + (-iyW^A[°\k) (9.6)
The index k runs only from 1 to y
—
1, since we need only half of the DFT
values and p = 0,1 (The computation of the output vectors with indices 0,
Y, and ^ is a special case that will be explained later.).
In order to obtain the first half output vectors as defined in Eq. (9.2),
the second quarter vectors are derived from the third quarter vectors using
the conjugate symmetry property as
N N 3N N N N N
-£) = {X(k+j),x(k+^)}
=
{X
(^-C--k)),x(-H--

The
2 x 1
PM DIT RDFT Algorithm
177
A'W(l)
=
J^^C
A'
(r+1)
(/1)
=
{A'Wi),4
r
\i)} o^ >> *o{4
r+1
\ii),4
r+1
\ii)}
Fig. 9.1 The SFG of the butterfly of the 2 x
1
PM DIT RDFT algorithm, where 1
< s <
•^. Twiddle factors are represented only by their exponents. The symbol
s
represents
TV
N SN N N N N
A
p
(^-k)
=
{X
(^-k),X(^-k)}
=
{X
Q-Q+k)),X(-+(--k))}
Therefore, Eqs. (9.5)
and
(9.6), for the vectors defined
in
Eq. (9.2), can
be
expressed
as
A'
p
(k)
=
A'(
e
\k)
+
(-iyW*4°Hk)
(9.7)
A'
p
(^-k)
= {4
e
\k)-(-l)*W?*4
0
Hk)}*, (9.8)
where
k =
1,..., j-
—
1 and
p =
0,1.
The
2x1 PM DIT
RDFT butterfly
In general,
the
relation governing the basic computation
at the rth
stage
can
be
obtained from Eqs. (9.7) and (9.8)
as
4
r+1
\h)
= 4
r
\h)
+
w^4
r
\i)
4
r+l
\h)
=
4
r
\h)-w^4
r
\i)
4
r+1
\n)
=
{4
r
\h)-w^4
r
\Dr
4
r+l
\n)
=
(4
r
\h)
+
w
s
N
+
*4
r
\i))*,
where
s is an
integer whose value depends on the stage of the computation
r and the index
h.
These equations characterize the input-output relation
of the
2 x 1
PM DIT RDFT butterfly, shown
in
Fig. 9.1. There are three
differences
at
the lower node between this butterfly and the butterfly of the
corresponding algorithm
for
complex data:
(i) the
result
of
the subtract
operation is stored as the first element in the output vector, (ii) the elements
of the output vector are conjugated,
and
(iii)
the
storage locations
of
the
input and output vectors are different.

178
DFT Algorithms for Real Data - II
The computational stages
There are m stages specified as r =
1,2,...,
m, where m = log
2
y-. A stage
consists of Y butterflies. The expressions for the twiddle factor exponent
and the indices of the nodes of each group of butterflies are given, for the
last m
—
2 stages, as follows (The butterflies of the first two stages and the
first butterfly of each group of butterflies of the other stages are special
cases and they will be explained later.).
h = imod2
r
'
2
, i =
0,1,...,
f - 1
s = 2
m
~
r
h
11 = 2
r
~
1
- h
I =
h
+ T-
1
(9.10)
The computation and storing of A' (^
—
k) in the last stage will erase some
of the input values for the computation of the butterfly indexed ^-
—
k.
Therefore, two butterflies with indices
A;
and y
—
k must be computed at
the same time in the algorithm implementation. The input values for the
computation of the butterfly indexed y
—
k can be temporarily stored in
the processor registers. A similar procedure is followed in implementing the
other stages.
For example, with N = 32, there are 4 stages specified as r = 1,2,3,
and 4. Four butterflies make up a stage. Indices h, I and
11,
and the twiddle
factor exponent s for each group of butterflies are given, respectively, by
(h = i mod 2
r
-
2
, {i = 0,1,2,3)), I = h+2
r
~
2
,11 = 2
r
~
1
-h, and s = 2
l
'
r
h.
Fig. 9.2 shows the SFG of the 2 x 1PM DIT RDFT algorithm, with N = 32.
Special butterflies
Unlike in the algorithms for complex data, the data values at one end of an
algorithm for real data is real and it is mostly complex at the other end.
This lack of symmetry of the data forces the use of special butterflies, the
/- and g-butterflies, those are specific for the algorithms of real data. These
butterflies process data values that may be pure real, pure imaginary, or
complex. The input/output relationship of an /-butterfly is as follows. Let
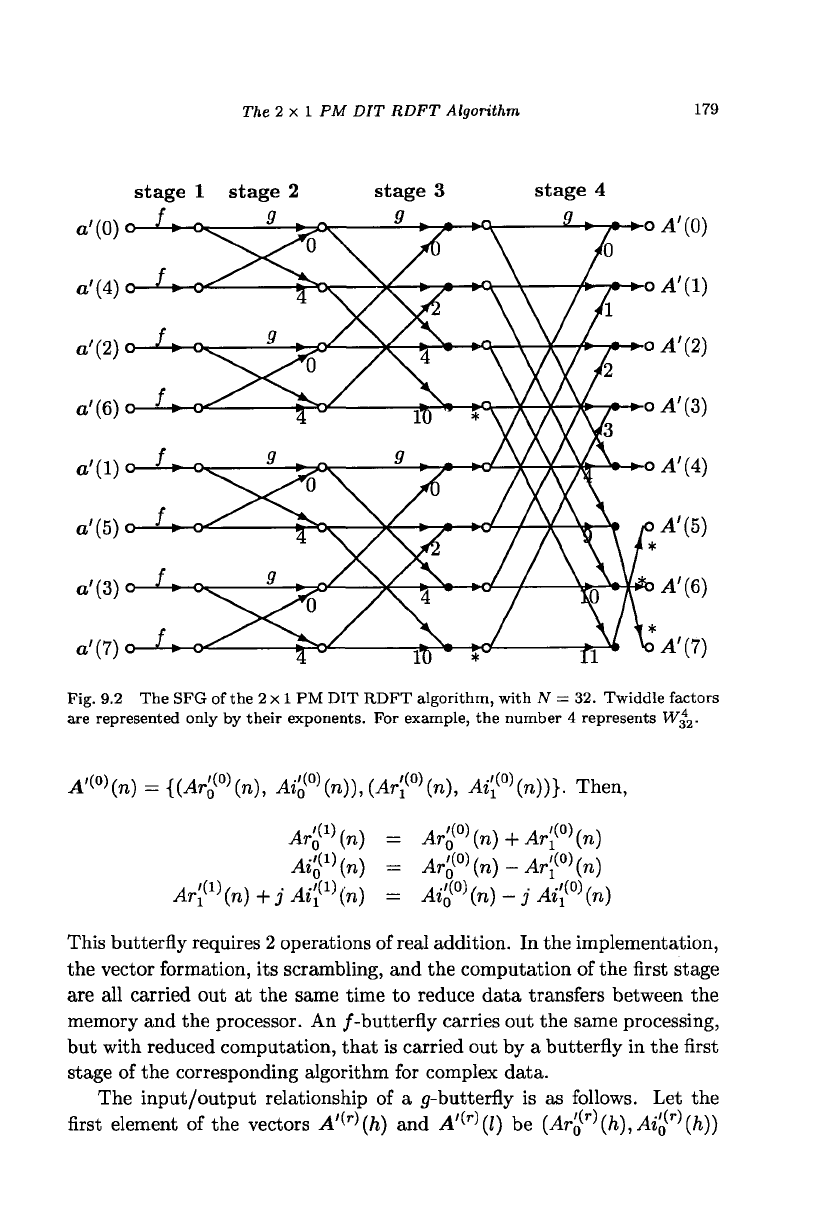
The 2 x 1 PM DIT RDFT Algorithm
179
stage 1 stage 2 stage 3 stage 4
Fig. 9.2 The SFG of the 2 x 1 PM DIT RDFT algorithm, with N = 32. Twiddle factors
are represented only by their exponents. For example, the number 4 represents W£
2
.
A'W{n)
= {(Ar$
0)
{n), Atd
(0)
(n)), (Ar'^in),
A<
(0)
(n))}.
Then,
Ar'
0
{1
\n) = Ar;
(0)
(n) + Ari
(0)
(n)
Ai'^in) = Ar'(
0)
(n)-Ar'{
0)
(n)
Ari
(1)
(n) + j A»i
(1)
(n) =
AZQ
(0)
(n) - j Aif
]
(n)
This butterfly requires 2 operations of real addition. In the implementation,
the vector formation, its scrambling, and the computation of the first stage
are all carried out at the same time to reduce data transfers between the
memory and the processor. An /-butterfly carries out the same processing,
but with reduced computation, that is carried out by a butterfly in the first
stage of the corresponding algorithm for complex data.
The input/output relationship of a 3-butterny is as follows. Let the
first element of the vectors A
,{
-
T
\h) and A'
W
(Z) be {Ar'
0
(r)
(h), Ai'
0
(r)
(h))

180
DFT Algorithms for Real Data - II
and (Ar'
0
ir)
(l),A4
r
\l)), respectively. Then,
A4
r
Hh)+ArS
r
Hl)
Ar$
r)
{h)-Ar$
r)
{l)
Atf\h)-jAi$
r
\l)
4
r
\h)
+
Wi4
r
\l)
A'±
r
\h)-WZA'{
r
\l)
This butterfly requires 2 operations of real multiplication and 8 operations
of real addition. The g-butterfly carries out the same processing, but with
reduced computation, that is carried out in the first and the middle but-
terflies of each group of butterflies, from the second stage onwards, in the
corresponding algorithm for complex data.
The software implementation of the PM RDFT algorithms is similar to
that of the PM DIT DFT algorithms for complex data with the differences
as explained above. A faster version can be obtained by implementing two
adjacent stages at a time. The number of real multiplications required by
an RDFT algorithm is one-half and that of additions is N
—
2 fewer than
one-half of that of the corresponding algorithm for complex data.
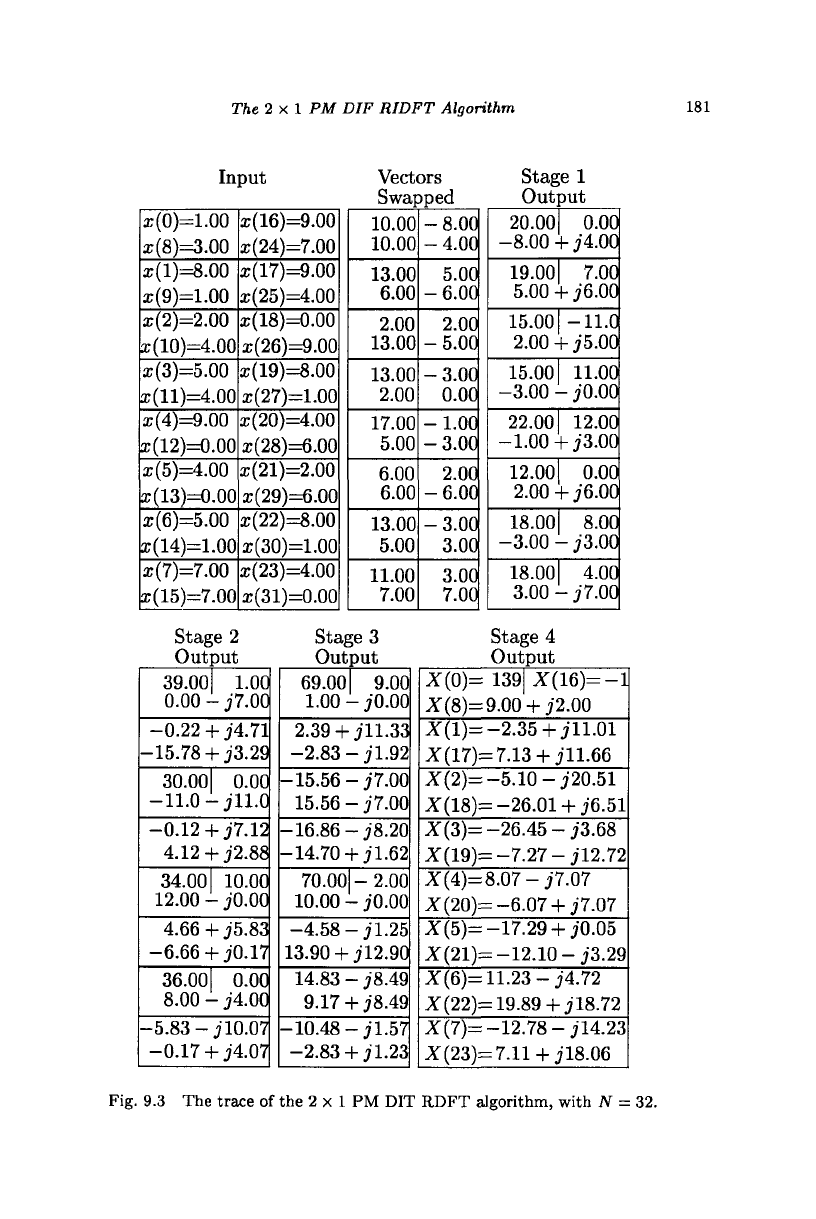
Example 9.1 A trace table of the algorithm, shown in Fig. 9.2, is shown
in Fig. 9.3. The first column shows how the 32 real data values are read into
the storage locations of 8 vectors each consisting of two complex elements.
When a value is pure real, it is shown separately with the use of a vertical
line.
The second column shows the values after vectors have been formed
and swapped. The third, fourth, fifth, and sixth columns show the values,
respectively, after the first, second, third, and fourth stage operations of the
algorithm are carried out. Compare this table with that given in Fig. 8.1
to find out how redundancy at each stage is eliminated. I
9.3 The 2x1 PM DIF RIDFT Algorithm
While the DFT of real data is hermitian-symmetric, the data itself is usu-
ally arbitrary. Therefore, it is relatively easier to eliminate the redundancies
starting from the DFT side of the SFG of the algorithm of complex data.
That is the reason we used the DIT approach to derive the RDFT algo-
rithm and we are going to use the DIF approach for deriving the RIDFT
algorithm.
Ar^
+1
\h) =
Ar'{
r+1)
(h)+jAi'}
r+1)
(h) =
4
r+1
\D
=
4
r+1
\i)
=
The 2 x 1 PM DIF RIDFT Algorithm
Input
x(2)=2.00
g(10)=4.00
a:(0)=1.00
x(8)=3.00
z(16)=9.00
s(24)=7.00
x(l)=8.00
g(9)=1.00
ar(17)=9.00
a;(25)=4.00
*(18)=0.00
s(26)=9.00
z(3)=5.00
z(ll)=4.00
x(4)=9.00
x(12)=0.00
z(5)=4.00
E(13)=0.00
a;(6)=5.00
g(14)=1.00
x(7)=7.00
j(15)=7.00
z(19)=8.00
s(27)=1.00
a;(20)=4.00
z(28)=6.00
z(21)=2.00
z(29)=6.00
z(22)=8.00
ar(30)=1.00
x(23)=4.00
g(31)=0.00
Vectors
Swapped
Stage 1
Output
10.00
10.00
13.00
6.00
2.00
13.00
13.00
2.00
17.00
5.00
6.00
6.00
13.00
5.00
11.00
7.00
-8.00
-4.00
5.00
-6.00
2.00
-5.00
-3.00
0.00
-1.00
-3.00
2.00
-6.00
-3.00
3.00
3.00
7.00
20.00 0.00
-8.00 + J4.00
19.00 7.00
5.00 +
j'6.00
15.00-11.0
2.00 + J5.00
15.00 11.00
-3.00 - jO.OO
22.00 12.00
-l.OO+j'3.00
12.00 0.00
2.00+J6.00
18.00 8.00
-3.00 - J3.00
18.00
3.00-
4.00
J7.00
Stage 2
Output
39.00
0.00-
1.00
j'7.00
-0.22 + J4.71
-15.78+ J3.29
30.00 0.00
-11.0-jll.O
-0.12 + J7.12
4.12 + J2.88
34.00
12.00 -
10.00
jO.OO
4.66 + J5.83
-6.66 + J0.17
36.00 0.00
8.00 - J4.00
-5.83-jl0.07
-0.17 + J4.07
-15.56 -J7.00
15.56 -J7.00
-16.86-J8.20
-14.70 + j 1.62
Stage 3
Output
69.00 9.00
1.00-jO.OO
2.39 + J11.33
-2.83-jl.92
70.00
10.00 -
-2.00
jO.OO
-4.58-jl.25
13.90+ J12.90
14.83 - J8.49
9.17 + J8.49
-10.48 -j 1.57
-2.83 +j 1.23
Stage 4
Output
X(0)=
X(8)=
139|
X(16)=
9.00 + j2.00
X(l)=
*(17)
-2.35 + jll.Ol
= 7.13 + jll.66
X{2)=-
*(18)=
-5.10-;20.51
-26.01+ J6.51
X(3)=
-y(i9)=
-26.45 - J3.68
=
-7.27-J12.72
•Y(20)
8.07 - J7.07
6.07 + J7.07
X(5)=
*(21)=
-17.29+ J0.05
=
-12.10 -J3.29
X{6)=
Jf(22)=
11.23 - J4.72
=
19.89 + j 18.72
X(7)=-
A" (23)=
-12.78 - j'14.23
7.11 + J18.06
Fig. 9.3 The trace of the 2 x 1 PM DIT RDFT algorithm, with N =

182 DFT Algorithms
for
Real Data
-
IT
To derive
the 2 x 1 PM DIF
RIDFT algorithm, consider
the
decompo-
sition
of an
y-vector IDFT into
two
^-vector IDFTs
in the
first stage
of
the
2 x 1 PM DIF
IDFT algorithm.
M2n)
= i E
(-V
pk
{Bo(k) +
(-l)
n+p
%B
0
(k
+ ^)}W2
nk
(9.H)
k=0
b
p
(2n
+
l) = ^^{-l^W^iBiW
fc=0
+
(-l)"+^{j)Bi{k+^)}Ws
nk
,
(9-12)
4
2
where
n
=
0,1,...,
^
— 1
andp
=
0,1.
The
input vectors,
B'(k),
as
defined
by
Eq. (9.3) are the
first half vectors.
The
expressions inside
the
pair
of
braces
in Eqs.
(9.11)
and
(9.12) require
the
first
and the
third quarter
input vectors
to
generate
the
first half input vectors (since
the
other half
is
redundant)
of the two
independent IDFTs, each
of
size
^
vectors. Thus,
we have
to
derive
the
third quarter input vectors from
the
second quarter
input vectors.
The
third quarter input vectors
can be
written
as
N
TV 1/V N 3/V
[j
+ k)
= {X(k+
I
-)
+
X(k+^),X(k+
1
)-X(k
+
—
N N N N
= {x(^-C-i-k))
+
x(-
+
(-
+
k)),
2
v
4 "
v
2
v
4
N
N N N
*(y
- (j -
*))
" X{-
+
(-+
k))},
(9.13)
where
q
=
0,1.
The
second quarter input vectors
can be
expressed
as
N
N 37V N 3N
B
9
Q-k)
=
{
X(j-k)
+
X(^--k),X(
J
-k)-X(—-k)}
N N N N
= {X(j-(j
+ k)) +
X(-
+
(--k)),
N N N N
X(j - (j
+ *))
- X{-
+
(--
k))}
(9.14)
Thus,
from
Eqs.
(9.13)
and
(9.14),
the
relation between
the
third quarter
and
the
second quarter input vectors
is
given
by
N
N N *
'
J
l+k)
=
{B
0
C--k),-B
1
(j-^*
B
q
{~
+k) =
{B
0
(- -
k), -Bi(
T
-
*)}
•
(9-15)

The 2 x 1 PM DIF RIDFT Algorithm
183
{B'
0
^(h),B'l
r
\h)} o .^ >° {fl^W.-B^W}
-*-T
Fig. 9.4 The SFG of the butterfly of the 2 x 1 PM DIF RIDFT algorithm, where
1 < s < 4r. Twiddle factors are represented only by their exponents. The symbol -s
represents W^'.
Therefore, Eqs. (9.11) and (9.12) can be expressed as
b
pi
2n
)
=
jj E ("
1
)
Pfc
{^o(fc) + (-l)"
+
^(5
0
(f - fc))*}WV**(9.16)
*=o
&
p
(2n + l) = i£(-l)**Wtf{i?i(*)
fc=0
- (-l)"+^(j)(Bi(^ - k))*}W£
nk
, (9.17)
4 2
where n = 0,l,...,^
—
1 and p = 0,1. The combination of the inputs
inside the pair of braces with indices k = 0, k = y, and k = ^ is a special
case that will be explained later.
The 2x1 PM DIF RIDFT butterfly
In general, the relation governing the basic computation, for the vectors
defined in Eq. (9.3), at the rth stage can be obtained from Eqs. (9.16) and
(9.17) as
B$
r+1
\h) = B'U{h) + {B$
r
\ll))*
B'}
r+1
\h) = B$'Hh) - (B$
r
\ll))*
B$
r+1
\t) = W^B'}
r
\h)-W-
8
-%(B'S
r
\ll))*
B'l
r+1)
(l) = WJB'l
r
\h) + W--*{B$
r)
(ll))*,
(9.18)
where s is an integer whose value depends on the stage of the computation
r and the index h. These equations characterize the input-output relation
of the 2 x 1 PM DIF RIDFT butterfly, shown in Fig. 9.4.
