Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

134 The

u x 1 PM DFT

Algorithms

where

s is an

integer whose value depends

on the

stage

computation

and the

index

h, and q =

0,1,...,

—

These equations characterize

the

u x 1 PM DIF DFT

butterfly

and

represent

2-point DFTs

and the

multiplication

of the

input values

appropriate twiddle factors.

The computational stages

There

are m

stages

computation specified

as r = 1,2,...,m,

where

log

^. The

number

butterflies that constitute

stage

is £.. The

expressions

for the

twiddle factor exponent

and the

indices

of the

nodes

each group

butterflies

are

given

follows.

zmod2

i =

0,1,...,

£. - 1

= h + 2

(6.12)

h(2

)

consequence

splitting

the

even

and the odd

indexed output vectors

over

the m

stages,

the

output vectors from

the

last stage

are

placed

in the

bit-reversed order.

6.6

The 2x1 PM DIF DFT

Algorithm

The

2x1 PM DIF DFT

butterfly

The

2x1 PM DIF

butterfly relations

are

deduced

substituting

value

for u in Eq.

(6.11).

a£

\h)

= aP(h) +

\l)

r+1

\h)

(/i)-a«(Z)

r+1)

^«M(fc)

<*aM(/)

(6J3)

where

s is an

integer whose value depends

on the

stage

computation

r and

the index

These equations characterize

the 2 x 1 PM DIF DFT

butterfly

shown

in Fig. 6.6.

This butterfly computes

two

2-point DFTs after

the

input values

are

multiplied

appropriate twiddle factors.

The

operation

of this butterfly

similar

that shown

in Fig. 6.1. The

difference

that

the twiddle factors corresponding

to the

second element

of the two

input

vectors

are W^ and (—j)W^,

respectively.

The

input

and

output vectors

Computational Complexity of the 2 X I PM DFT Algorithms 135

= {aW(/

),ai

(ft)} o, >^o ={4

r+1)

(/i),a(

r+1)

(/i)}

a(r)(

{

a«(/),aW(0} o-^^o °

(rf

(

r+1,

(0,«i

r+1)

(0}

Fig. 6.6 The SFG of the butterfly of the 2 x 1 PM DIF DFT algorithm, where 0 < s <

x- Twiddle factors are represented only by their exponents. The symbol s represents

are represented by the symbol a just to indicate that the decomposition

process of an ^—vector DFT starts from the input side.

The computational stages

For example, with N = 16, there are 3 stages specified as r = 1,2, and

Four butterflies make up a stage. Indices h and /, and the twiddle

factor exponent s of each group of butterflies are given, respectively, by

(ft = (i mod 2

), (i =

0,1,...,

3)), I = h + 2

, and s =

h(2

The SFG of the 2 x 1 PM DIF DFT algorithm, with N = 16, is shown in

Fig. 6.7. The grouping of the butterflies is just the reverse of that shown

in Fig. 6.2, since the decomposition of the problem starts from the input

side.

The input and output vectors have the same interpretations as in

Fig. 6.2, except that the input vectors are placed in the natural order and

the output vectors are placed in the bit-reversed order.

Example 6.2 Figure 6.8 shows the trace of the algorithm shown in

Fig. 6.7. Vector formation is similar to that in Example 6.1 except that

the vectors, shown in the second column, are placed in natural order. The

third, fourth, and fifth column vectors are obtained after the first, second,

and third stage operations of the algorithm are carried out. The output

vectors have to be swapped to put them in sequential order. I

6.7 Computational Complexity of the 2 x 1 PM DFT

Algorithms

In this section, the computational complexity of the 2x1 PM DIT DFT

algorithms is described. The computational complexity of the DIF algo-

rithms is the same as that of the DIT algorithms.

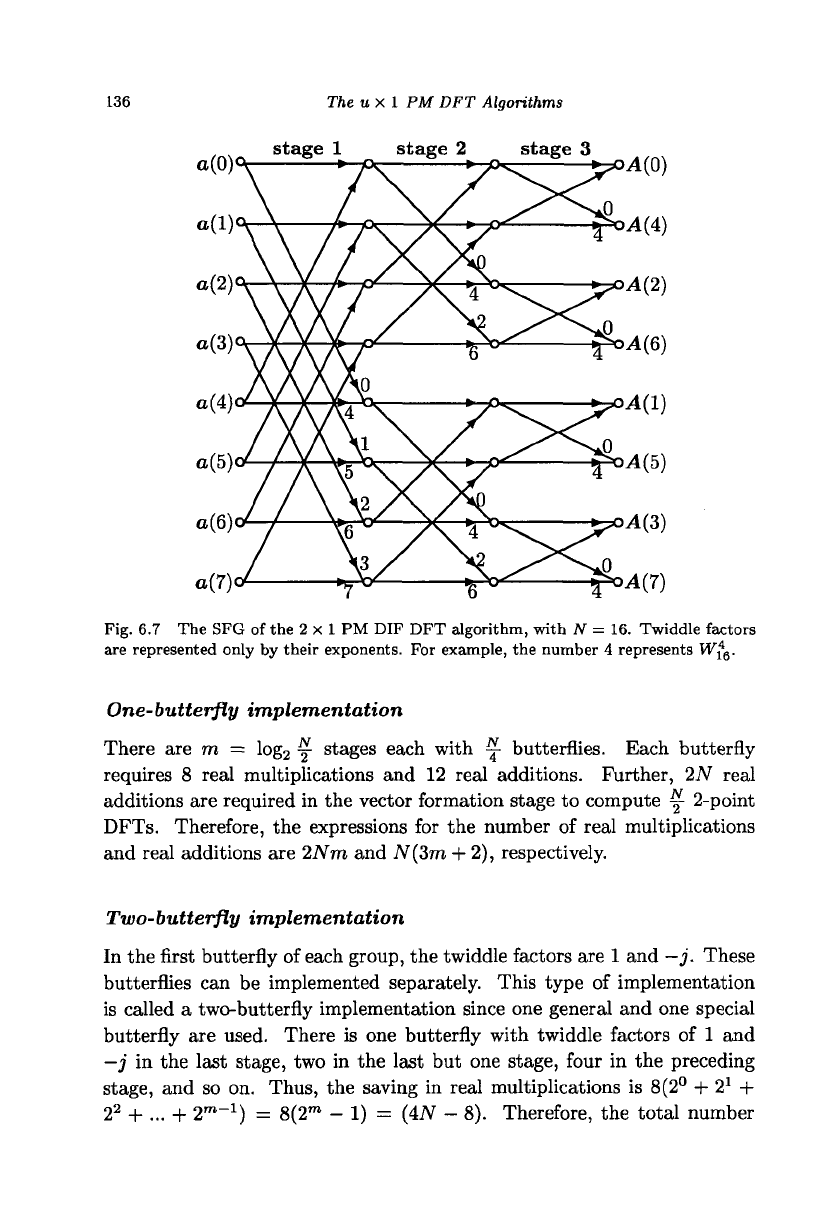
136 The u x 1 PM DFT Algorithms

Fig. 6.7 The SFG of the 2 x 1 PM DIF DFT algorithm, with N = 16. Twiddle factors

are represented only by their exponents. For example, the number 4 represents W±

One-butterfly implementation

There are m = log

y stages each with

—•

butterflies. Each butterfly

requires 8 real multiplications and 12 real additions. Further, 2N real

additions are required in the vector formation stage to compute y 2-point

DFTs.

Therefore, the expressions for the number of real multiplications

and real additions are 2Nrn and TV (3m + 2), respectively.

Two-butterfly implementation

In the first butterfly of each group, the twiddle factors are 1 and —

These

butterflies can be implemented separately. This type of implementation

is called a two-butterfly implementation since one general and one special

butterfly are used. There is one butterfly with twiddle factors of 1 and

-j in the last stage, two in the last but one stage, four in the preceding

stage, and so on. Thus, the saving in real multiplications is 8(2° + 2

+ ... + 2

m_1

) = 8(2

- 1) = (47V - 8). Therefore, the total number

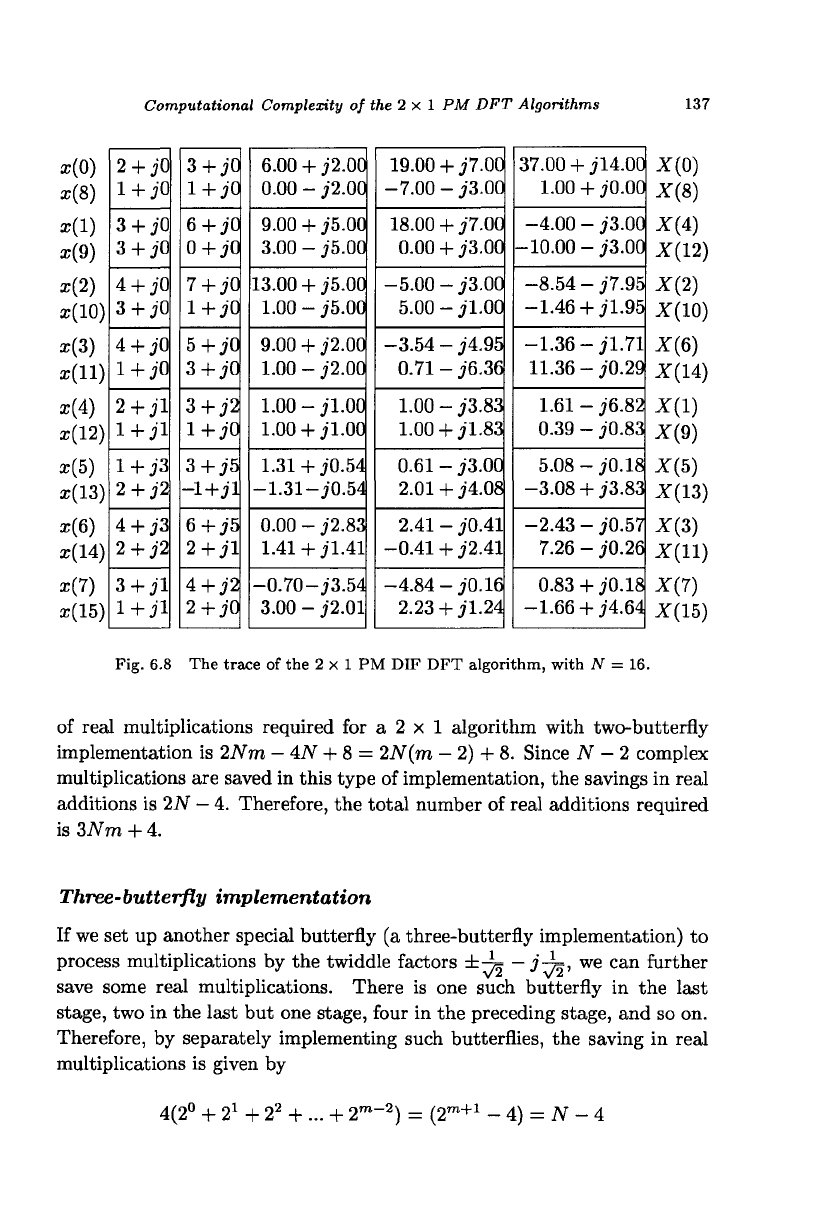
Computational Complexity of the 2 x 1 PM DFT Algorithms 137

x(0)

x(8)

ar(l)

x(9)

x(2)

x{W)

ar(3)

x(ll)

*(4)

s(12)

*(5)

x(13)

x(6)

a;(14)

*(7)

z(15)

2 + jO

1+jO

3 + jO

4 + jO

3 + jO

4 + jO

1 + jO

2 + jl

1 + jl

1 + J3

2 + j2

4 + J3

2 + J2

3 + jl

1+jl

3 + jO

1+jO

6+jO

0+jO

7 + jO

1+jO

5 + jO

3 + jO

3 + J2

1+jO

3 + J5

-1+jl

6+j5

2+jl

4 + J2

2+jO

6.00 +

j'2.00

0.00 - J2.00

9.00 + J5.00

3.00 -

j'5.00

13.00 + J5.00

1.00 - J5.00

9.00 +

j'2.00

1.00 - J2.00

l.OO-jl.OO

1.00 + jl.OO

1.31 + J0.54

-I.31-j0.54

0.00 -

j'2.83

1.41+J1.41

-0.70-j3.54

3.00 - J2.01

19.00 + J7.00

-7.00 - J3.00

18.00 +

j"7.00

0.00 + J3.00

-5.00-j3.00

5.00 - jl.00

-3.54 -

j'4.95

0.71 - J6.36

1.00 - J3.83

l.OO + jl.83

0.61 - j3.00

2.01 + J4.08

2.41 -

j'0.41

-0.41 + J2.41

-4.84-j0.16

2.23 + J1.24

37.00 + j'14.00

1.00 + jO.OO

-4.00 -

j/3.00

-10.00-J3.00

-8.54 - J7.95

-1.46 + J1.95

-l.36-jl.71

11.36 - jO.29

1.61

0.39

J6.82

J0.83

5.08 -jO. 18

-3.08 + J3.83

-2.43 - J0.57

7.26 - jO.26

0.83 + J0.18

-1.66 + J4.64

X(0)

X(8)

X(4)

X(12)

X{2)

X(10)

X(6)

X(U)

X(l)

X(9)

X(5)

X(13)

X(3)

X(ll)

X(7)

X(15)

Fig. 6.8 The trace of the 2 x 1 PM DIF DFT algorithm, with N = 16.

of real multiplications required for a 2 x 1 algorithm with two-butterfly

implementation is 2Nm -AN + 8 = 2N(m - 2) + 8. Since N - 2 complex

multiplications are saved in this type of implementation, the savings in real

additions is 2N

—

4. Therefore, the total number of real additions required

is 3Nm + 4.

Three-butterfly implementation

If we set up another special butterfly (a three-butterfly implementation) to

process multiplications by the twiddle factors ±4s

—

775,

we can further

save some real multiplications. There is one such butterfly in the last

stage, two in the last but one stage, four in the preceding stage, and so on.

Therefore, by separately implementing such butterflies, the saving in real

multiplications is given by

4(2° + 2

+ 2

+ ... + 2

) = (2

m+1

- 4) = N - 4

138 The u

1 PM DFT Algorithms

Table 6.1 Figures of Computational Complexity for the 2x1 PM DFT Algorithm with

Various Number of Butterflies.

Number of multiplications | Number of additions

1-B_fly

2-B_fly 3-B_fly

1-Bjfly

2- fc 3-B_fly

128

256

512

1024

2048

4096

256

640

1536

3584

8192

18342

40960

90112

136

392

1032

2568

6152

14344

32776

73736

108

332

908

2316

5644

13324

30732

69644

176

448

1088

2560

5888

13312

29696

65536

143360

148

388

964

2308

5380

12292

27652

61444

135172

There is no further reduction in the number of real additions. Therefore,

for the 3-butterfly implementation, the expressions for the number of real

multiplications and real additions are N(2m

—

5) + 12 and 3Nm + 4, re-

spectively. The number of each of the two operations of real multiplication

and real addition required by the 2x1 PM algorithm for complex data

for various values of N and for various number of butterflies is given in

Table 6.1.

Twiddle factor generation

Twiddle factors for the general butterflies indexed h and

—

h for the

DIT algorithms (h and ^qr

h f°

the DIF algorithms) are trivially related

and, therefore, they need to be referenced or computed only once if the two

butterflies are processed at the same time. Twiddle factors for the first

butterfly are of the form Wfc and W^ and those of the second butterfly

—-8 — -8

are of the form WJ and W£ . The size of the look-up table to store

the twiddle factors is ^ which is one-eighth of that of the data. Twiddle

factors can also be generated as they are required but the computation time

will increase.

6.8 The 6x1 PM DIT DFT Algorithm

The DFT lengths that are most often used in practice are integral powers

of two. However, for a specific requirement, it is relatively straightforward

The 6x1 PM DIT DFT Algorithm

139

to develop efficient algorithms for DFT lengths with a factor such as 3,5,7,

etc.

For example, using a vector with six elements, that is u = 6, we can

design algorithms with DFT lengths 12, 24, 48, 96,192, 384, etc. The input

vectors are formed by computing 6-point DFTs of the input data as defined

in Eq. (5.2). The prime-factor algorithm described in Appendix D can be

used to compute the 6-point DFTs efficiently.

The 6x1 PM DIT DFT butterfly

The input-output relations of a butterfly of the 6 x 1 PM DIT DFT algo-

rithm can be easily deduced from Eq. (6.5), by substituting u = 6, as

r+1)

(r+1)

r+1)

{r+1

{r+l

(r+1

r+1

(h)

Hi)

\h)

{h)

(h)

+ w^4

-WS,A£HI)

„.«+£ .(VI

-4

• "JV "4'(0

-W

^A^(l)

^A^Hl)

+ w^

+f+

-w#"«

+ia

+ w

+6+i

-4

(o,

where s is an integer whose value depends on the stage of computation r

and the index h. These equations characterize the 6x1 PM DIT DFT

butterfly. This butterfly computes six 2-point DFTs after the input values

indexed I are multiplied by appropriate twiddle factors. The differences

between this butterfly and that shown in Fig. 6.1 are: (i) three 2-point

DFTs are computed at each output node rather than one and (ii) the twid-

dle factors are different. This butterfly requires 24 real multiplications, 36

real additions, and assuming that sufficient number of registers is available

in the processor, 48 data transfer operations between the memory and the

processor. There are ^ log

y butterflies. Two special butterflies with

reduced computation can be derived when s = 0 and s = ^. The first but-

140

The u x 1 PM DFT Algorithms

terfiy requires 16 real multiplications and 32 real additions while the second

butterfly requires 20 real multiplications and 36 real additions. There are

—

1 butterflies of the first type and ^

—

1 of the second type. The six

twiddle factors required for the butterfly operation can be obtained by gen-

erating only three of them. Specifically, if the twiddle factors Wfc, W

8+ &- 8+ ^-+ ^-

and W

are generated, then the remaining twiddle factors W

6 12

, and W

B 12

are obtained simply by multiplying, respectively,

the first three twiddle factors with W£ = —j.

The computational stages

For example, with N = 48, there are 3 stages specified as r = 1,2, and

Four butterflies make up a stage. Indices h and /, and the twiddle

factor exponent s of each group of butterflies are given, respectively, by

(h = i mod 2

-\ (i =

0,1,...,

3)), l = h + 2

~\ and s =

h(2

The

SFG of the 6 x 1 PM DIT DFT algorithm, with N = 48, is the same as

that shown in Fig. 6.2 with u = 2 and N = 16, but the number of 2-point

DFTs computed by each butterfly is six rather than two.

The computational complexity

For a

1-butterfly

implementation, the number of real multiplications and

real additions required are given, respectively, by 2Nm + ^ and 3Nm +

6N, where m = log

j--

For a 2-butterfly implementation, the number of

real multiplications and real additions required are given, respectively, by

2iVm+8 and 3JVm+ ^§^+4. For a 3-butterfly implementation, the number

of real multiplications and real additions required are given, respectively,

by 2Nm - f + 12 and 3Nm + ^- + 4. The number of each of the two

operations of real multiplication and real addition required by the 6x1

PM DIT algorithm for complex data for various values of N and various

number of butterflies is given in Table 6.2.

Example 6.3 A trace table of the 6 x 1 PM DIT DFT algorithm, with

N = 24, is shown in Fig. 6.9. The result of vector formation and swapping

is shown in column two. The third and fourth column vectors are obtained

after the first and second stage operations of the algorithm are carried out.

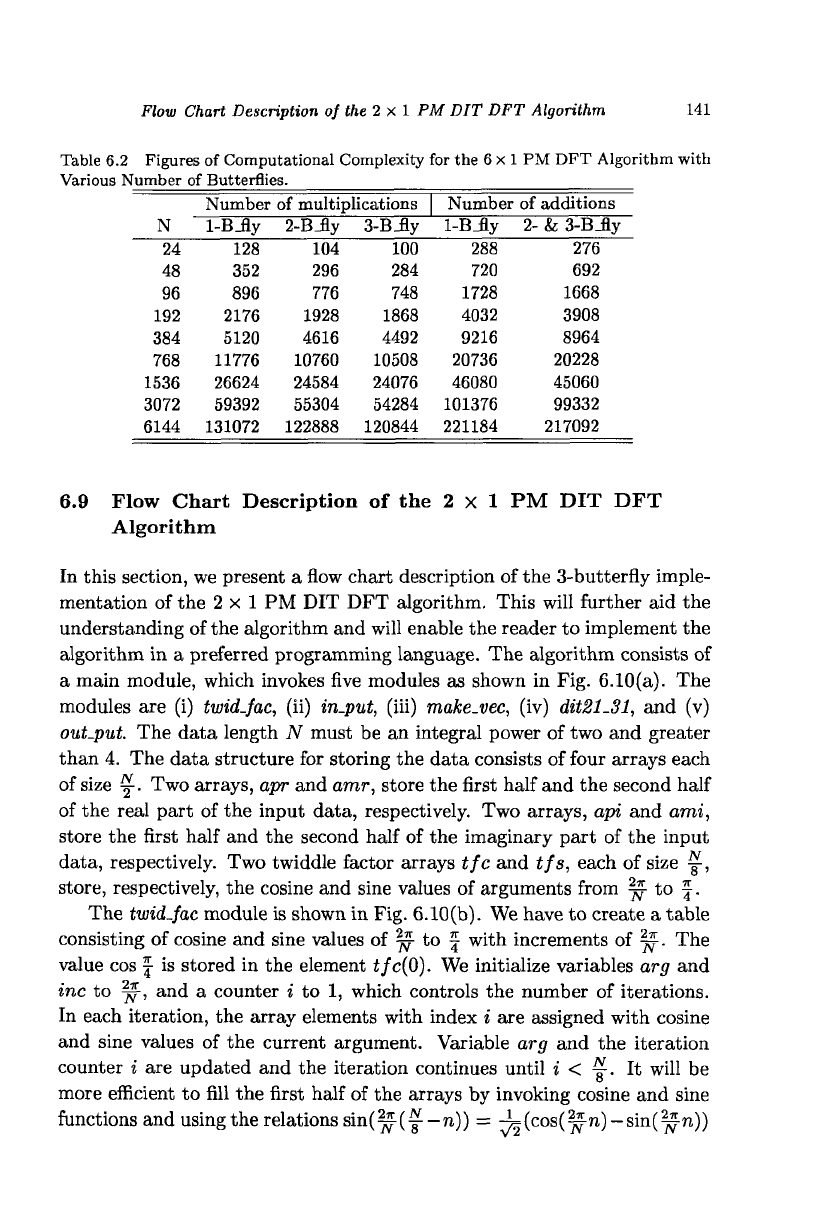
Flow Chart Description of the 2 x 1 PM DIT DFT Algorithm 141

Table 6.2 Figures of Computational Complexity for the 6x1 PM DFT Algorithm with

Various Number of Butterflies.

192

384

768

1536

3072

6144

Number

multiplications

1-B_fly

128

352

896

2176

5120

11776

26624

59392

131072

2-B_fly

104

296

776

1928

4616

10760

24584

55304

122888

3-B_fly

100

284

748

1868

4492

10508

24076

54284

120844

Number

additions

1-BJy

288

720

1728

4032

9216

20736

46080

101376

221184

3-B_By

276

692

1668

3908

8964

20228

45060

99332

217092

6.9 Flow Chart Description of the 2 x 1 PM DIT DFT

Algorithm

In this section, we present a flow chart description of the 3-butterfly imple-

mentation of the 2 x 1 PM DIT DFT algorithm. This will further aid the

understanding of the algorithm and will enable the reader to implement the

algorithm in a preferred programming language. The algorithm consists of

a main module, which invokes five modules as shown in Fig. 6.10(a). The

modules are (i) twid-fac, (ii) iti-put, (iii) make.vec, (iv) dit21Sl, and (v)

out-put. The data length N must be an integral power of two and greater

than 4. The data structure for storing the data consists of four arrays each

of size y. Two arrays, apr and amr, store the first half and the second half

of the real part of the input data, respectively. Two arrays, api and ami,

store the first half and the second half of the imaginary part of the input

data, respectively. Two twiddle factor arrays tfc and tfs, each of size y,

store, respectively, the cosine and sine values of arguments from ^ to j.

The twidjac module is shown in Fig. 6.10(b). We have to create a table

consisting of cosine and sine values of ^ to \ with increments of ^. The

value cos J is stored in the element tfc(0). We initialize variables arg and

inc to ^F, and a counter i to 1, which controls the number of iterations.

In each iteration, the array elements with index i are assigned with cosine

and sine values of the current argument. Variable arg and the iteration

counter i are updated and the iteration continues until i < %-. It will be

more efficient to fill the first half of the arrays by invoking cosine and sine

functions and using the relations sin(^(y-n)) = -^(cos(^n)-sin(^n))

142

The u x 1 PM DFT Algorithms

x(0)

x(4)

x(8)

x(12)

z(16)

z(20)

*(1)

x{h)

x(9)

x(13)

*(17)

a:(21)

x(2)

x(6)

x(10)

z(14)

ar(18)

z(22)

x(3)

x{7)

x(U)

z(15)

x(19)

x(23)

2 + jl

1-J3

3+J2

1+J2

3+jl

1+J2

1-J2

O-jl

1-Jl

3 4-J3

-2 - j2

3+J2

3-jl

1+J2

2 + jO

2-n

-1 + J3

2+jO

2+J2

2+J3

3-jl

-2 + J2

-2 - j3

-1-J2

11.00+ J5.00

-4.46 - J3.00

-6.20 + J2.00

5.00 + J3.00

4.20 + J2.00

2.46 - J3.00

9.00 + J3.00

1.13 -

j'2.23

7.33 - jl.04

-1.00 + jl.OO

-l.33-j7.96

2.87 + jl.23

6.00 - jl.00

-1.73 -

j'3.00

-0.46 4-j7.20

-6.00 - J9.00

6.46 -

j'3.20

1.73 -

j'3.00

2.00 + jl.OO

10.06 -

j'4.43

1.60 +

j'7.23

4.00 - J5.00

-3.60 4-j3.77

-2.06 + J9.43

20.00 4-j8.00

-3.43 - J4.87

-2.04 + J7.13

2.00 + J2.00

-8.96 4-j8.87

10.43 -j'3.13

-4.60 - J5.50

6.00+J4.00

0.60-J5.50

-4.33 - jO.50

4.00 + j2.00

4.33-J0.50

8.00 + jO.OO

6.60+J9.43

11.53-jl.96

4.00 - j2.00

-7.53 4-j4.96

1.40-J4.43

4.77-J11.87

-11.0-J13.0

8.23 - jlO.13

-8.23 4-j5.87

-l.00-j5.00

-4.77 4-j4.13

28.00

J8.00

2.03 -

j'3.83

-0.90 + J12.90

12.00 4-

j'8.00

-6.10 4-jl8.10

-17.03 4-j4.83

-3.06 -j 18.20

-7.06 -j 16.07

1.17 4-J6.24

-6.13 4-j7.20

8.26 4- J5.07

6.83 - J2.24

7.00

jO.OO

0.00 - J2.00

7.00

jO.OO

-13.86 - J9.73

4.00

j'6.00

13.86 -

j'6.27

-10.974-j2.59

3.47 4-J5.93

10.01 - J3.26

22.97

J5.41

-12.13-J6.93

-l.35 4-j2.26

X(0)

X(4)

X(8)

X(12)

X(16)

X(20)

X(l)

X(5)

X(9)

X(13)

X(17)

X(21)

X{2)

X(6)

X(10)

X(U)

X(18)

X(22)

X(3)

X(7)

X(ll)

X(15)

X(19)

X(23)

Fig. 6.9 The trace of the 6 x 1 PM DIT DFT algorithm, with N = 24.

and cos(^(y - n)) = -^(cos^n) 4- sin(^n)) to fill the second half at

the same time. Note that this module can be eliminated by computing the

cosine and sine values as required. However, it will be costly in terms of

run-time.

The in.put module for reading the data is shown in Fig. 6.10(c). It

is assumed that the input data is available with N real values followed

by N imaginary values. There are y elements in each of the four arrays,

apr,amr,api, and ami. Each quarter of the input values are read into,

respectively, into the four arrays. If the input data is real-valued, arrays

api and ami must be initialized to zero.

The make-vec module for making and swapping vectors is shown in

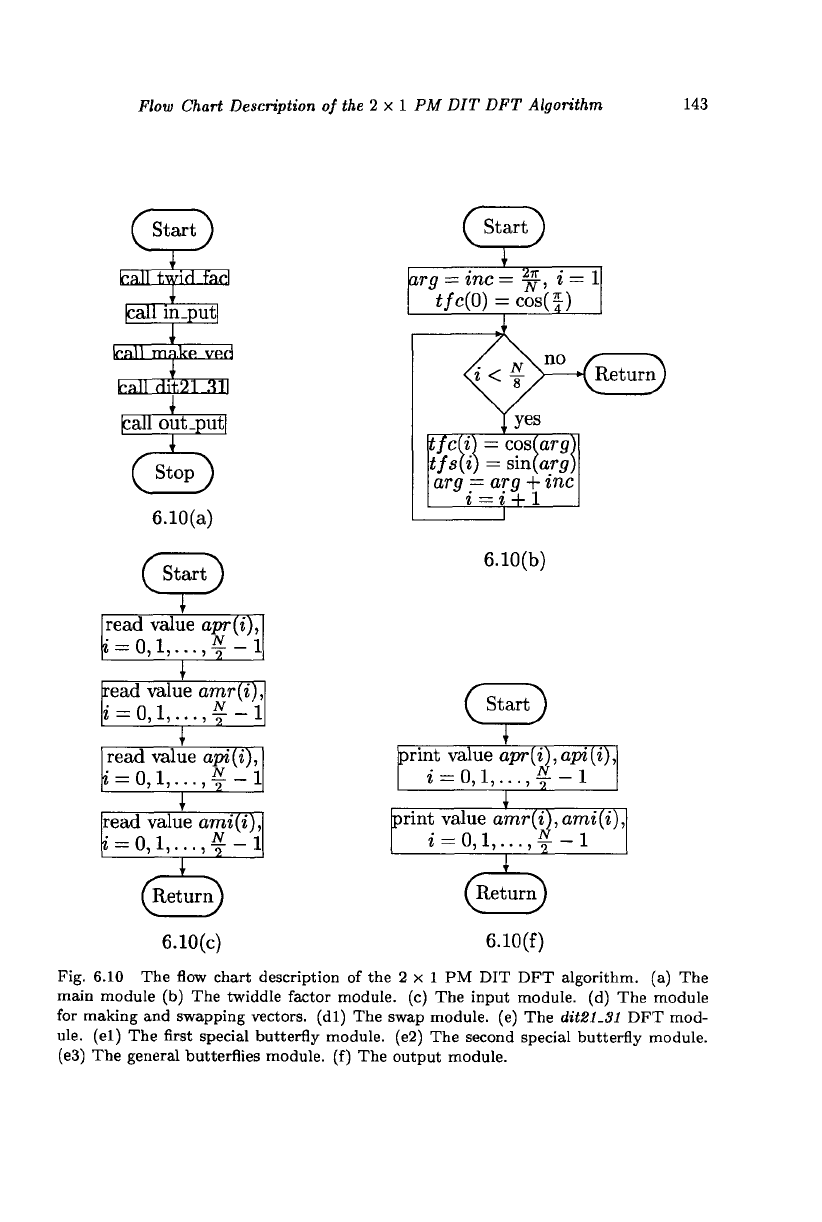
Flow Chart Description of the 2 x 1 PM DIT DFT Algorithm 143

(start)

lra.ll twiri facl

|call in-put|

leal

make veri

hall HiUl 311

|call out-put|

( Stop*)

6.10(a)

f Start")

read value apr(i),

^ = 0,1,...,£-1

read value amr(i),

t = 0,l,...,g-l

read value api(i),

|i = 0,

!,...,£-!

read value amz(i),

i =

0,l,...,*_-l

(Return)

6.10(c)

(Start)

ar-^

—

i*r\n

— -^ZL

N '

t/c(0) = cos(|)

•T

Return)

£/c(i) = cosfarp

tfs(i) = sin(ar</

ar<7 = org + inc

i = i + 1

6.10(b)

("start)

print value apr(i),

= 0,1,...,£

print value

i = 0,1

amr(i),

•• •' T

aj»(*)>

-1

amz(i),

-1

( Return)

6.10(f)

Fig. 6.10 The flow chart description of the 2 x 1 PM DIT DFT algorithm, (a) The

main module (b) The twiddle factor module, (c) The input module, (d) The module

for making and swapping vectors, (dl) The swap module, (e) The dit21.31 DFT mod-

ule.

(el) The first special butterfly module. (e2) The second special butterfly module.

(e3) The general butterflies module, (f) The output module.