Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications
Подождите немного. Документ загружается.


84
Properties of the DFT
That is the circular convolution of two time-domain sequences is obtained
by taking the IDFT of the product of the DFTs of the individual sequences.
Substituting the corresponding DFT expressions for X(k) and H(k), we get
1
jv-i jv-i tf-i
y^
= ]v £<£ x(m)W^}{^2
h(l)W
l
N
k
}W^
k
k=0 m=Q 1=0
Rearranging the summation, we get
m=0 1=0 ifc=0
The rightmost summation is equal to N for / = n
—
m and zero otherwise.
Therefore,
7V-1
y(ri) = 22 x(m)h(n
—
m)
m=0
Example 4.25 Convolve x(n) = {1,4,2,0} and h{n) =
{2,3,0,1}.
X(*) = {7,-1-J4
>
-1,-1 + J4} and tf(fc) = {6,2 - j2, -2,2 + j2}
X(k)H(k)
=
{42,-10-J6,2,-10
+
J"6}
The product is obtained by multiplying the corresponding terms in the
two sequences. The IDFT of X(k)H(k) is the convolution sum, y(n) =
{6,13,16,7} I
Circular convolution in the frequency-domain
The circular convolution of two frequency-domain sequences, X(k) and
H(jfe),
k =
0,1,...,
N - 1, divided by N is obtained by taking the DFT of
the product of the IDFTs of the individual sequences.
1
JV_1
1
N
~
l
Y(k)
x(n)h(n) & - J2 X(m)H(k -"»)=-£ H(m)X(k - m) = -j^,
m=0 m=0
where Y(k) is the convolution of the sequences X(k) and H(k) and k =
0,l,...,iV-l.
Example 4.26 The product of x(n) and h(n) given in Example 4.25 is
{2,12,0,0}.
The DFT of this sequence is {14,2-j
12,
-10,2 +jl2}= ^.1

Sum and Difference of Sequences
85
Circular correlation of time-domain sequences
The circular cross-correlation of two time-domain sequences x(n) and h(n),
n =
0,1,...,
N
—
1 is given by
7V-1
y
X
h(n)
= ^2x*(m)h(n + m), n-0,l,...,N-l,
771=0
where x*(m) is the complex conjugate of x(m). Note that, for real sig-
nals,
x*(m) = x(m). This equation can also be written, in terms of the
convolution operation, as
JV-l
y
x
h(n)
= ^x*(N -m)h(n-m), n = 0,1,...,JV - 1,
771=0
where x*(N
—
m) = ID FT of
X*(k).
Therefore, the circular correlation
of two time-domain sequences can be obtained by taking the ID FT of the
product of the complex-conjugate of the DFT of the first sequence and the
DFT of the second sequence.
y
xh
(n)
= IDFToi (X*(k)H(k))
Vhx(n) = y*
xh
(N-n)= IDFT of (H*(k)X(k))
Example 4.27 For the sequences in Example 4.25
y
xh
(n)
= {14,5,8,15} and
y
hx
(n)
= {14,15,8,5} I
The autocorrelation operation is the same as the cross-correlation op-
eration with x(ri)
—
h(n).
y
xx
(n)=
IDFTof(|X(fc)|
2
)
Example 4.28 For the sequence {2,3,0,1}, we get
y
xx
{n)
={14,8,6,8}.l
4.9 Sum and Difference of Sequences
Since
A;
= 0, the values of all the Wfi
k
terms in the DFT definition is just
one and the value of X(0) is the sum of the input sequence x(n).
N-l
X(0) = £
x(n)
71=0

86
Properties of the DFT
With an even N and k = y-, the input sequence values are alternately
multiplied by 1 and
-1.
Therefore,
N-2 JV-1
*(y>
=
£
*(»)
- £ *(»)
n=0,2 n=l,3
Example 4.29
x(n) = {2,1,3,4} & Jf(fc) = {10,-1 + ^3,0,-1-^3}
X(0) = 2 + l + 3 + 4 = 10 and X(2) = (2 + 3) - (1 + 4) = 0 I
In the case of the IDFT,
*(°) =
Jf
E
X
W
With an even N,
^y
2
TV —1
*(y)
=
^( £*(*)- £*(*))
fc=0,2 fc=l,3
Example 4.30 For the x(n) and X(k) given in the earlier example,
a:(0) = i(10-l+j3 + 0-l-j3) = ^ = 2
a:(2) = |(10 + l-j3 + 0+l+i3) = j=
3
'
These values can be used as a preliminary check of the output of an algo-
rithm to compute the DFT or the IDFT.
4.10 Padding the Data with Zeros
Padding the data with zeros at the end
Let x(n) O- X(k), n, k =
0,1,...,
N
—
1. If we pad x(n) with zeros to get
y(n),
n =
0,1,...,
mN
—
1 defined as
, . _ f x(n) for n = 0,l,...,iV-l
VW - | Q otherwise

Padding the Data with Zeros
87
where m is any positive integer, then,
Y(mk)=X{k), fc = 0,l,...,iV
The DFT of the signal y(n) is given by
mN-l
Y(k)= Y, y(n)W£
k
N
, h = 0,1,-••,mN-l
n=0
Since y(n) is zero for n > N
—
1, we get
JV-l
Y(k)=Y,y(n)
w
™N, k = 0,l,...,mN-l
n=0
Substituting mk for
A;
and simplifying, we get
JV-l
Y(mk)= Y^y{n)Wtf =X(k), k =
0,1,...
,JV - 1
n=0
Example 4.31 Let m = 2 and x(n) =
{2,1,4,3}.
X(k) = {10,-2 +
j2,2,-2-j2}.
Then,
y(n) = {2,1,4,3,0,0,0,0}^
Y{k) = {10,*,-2 + j2,*,2,*,-2-j2,*}
By zero padding, the frequency increment of the spectrum is halved. There-
fore,
the spectral values with indices 0,1,2,3 in X(k) become spectral values
with indices 0,2,4,6 in Y{k). I
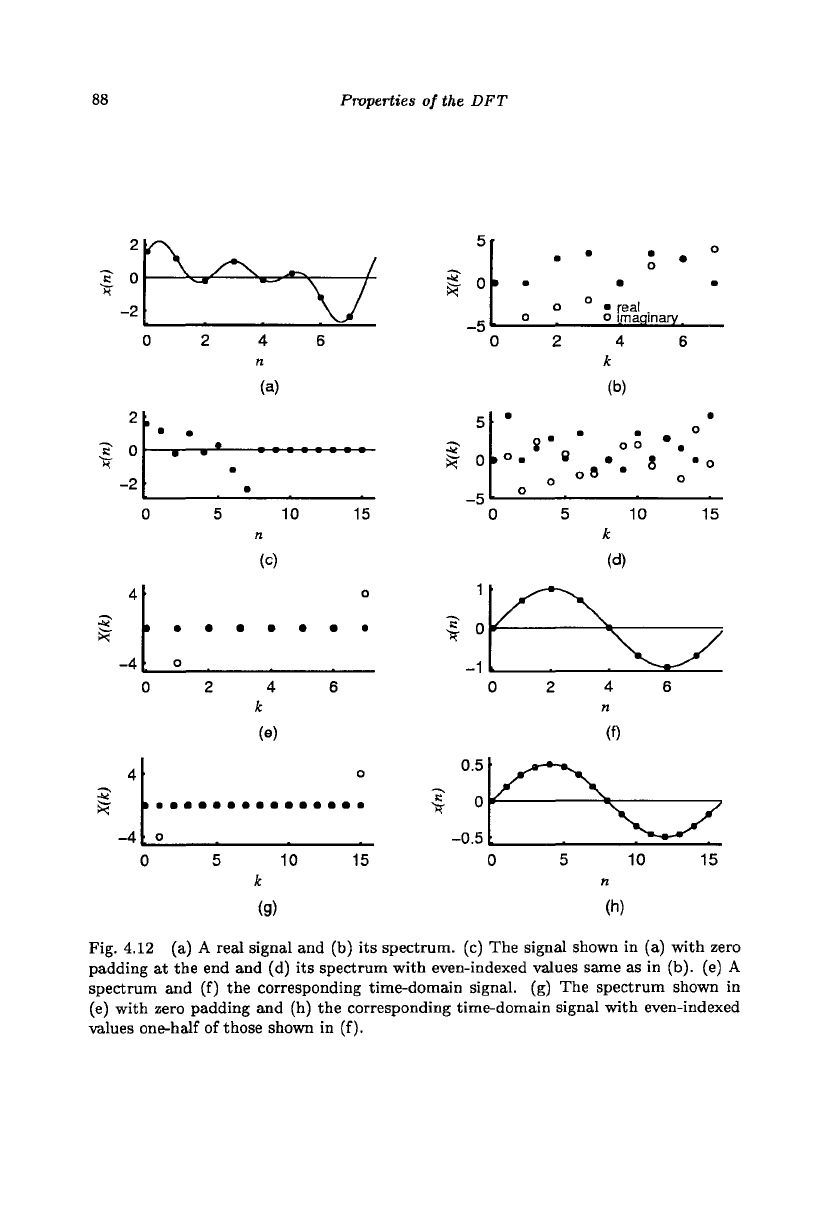
Figures 4.12(a) and (b) show, respectively, a signal with eight samples and
its spectrum. Figures 4.12(c) and (d) show, respectively, the same signal
padded up with eight zeros at the end and the corresponding spectrum. The
even-indexed spectral values are the same as those shown in Fig. 4.12(b).
The odd-indexed spectral values are not specified by this theorem. By zero
padding at the end, we get interpolation of the spectral values.
A similar effect is observed in zero padding a spectrum. Figures 4.12(e)
and (f) show, respectively, a spectrum with eight samples and the corre-
sponding time-domain signal. Figures 4.12(g) and (h) show, respectively,
the same spectrum padded up with eight zeros in the middle of the spec-
trum (at the end in the center-zero format) and the corresponding time-
domain signal. The even-indexed signal values are one-half of those shown
Properties of the DFT
~
2
W
? n X:
£ 0
K
-2
5f
^~
2 4 6
n
(a)
£ °
5 10 15
n
(c)
-4 o
2 4 6
k
(e)
5 10 15
k
(9)
£ °
• real
o imaginary
5
Sf 0
-5
(b)
8" oS «.
o °
8
o
5 10 15
(d)
(h)
Fig. 4.12 (a) A real signal and (b) its spectrum, (c) The signal shown in (a) with zero
padding at the end and (d) its spectrum with even-indexed values same as in (b). (e) A
spectrum and (f) the corresponding time-domain signal, (g) The spectrum shown in
(e) with zero padding and (h) the corresponding time-domain signal with even-indexed
values one-half of those shown in (f).

Padding the Data with Zeros
89
in Fig. 4.12(f). By zero padding at the end in the frequency-domain, we
get interpolation of the time-domain samples.
Padding the data with zeros in between the samples
Let x(n) O X(k), n, k =
0,1,...,
N
—
1. If we pad x(n) with zeros to get
y{n),
n =
0,1,...,
mN
—
1 defined as
{?
, . _ . x{n) for n =
0,1,...,
N
'
n
otherwise
where m is any positive integer, then,
Y{k) = X(k modN), k = 0,1,. ..,mN - 1
The DFT of the sequence y(n) is given by
mJV-l
Y{k)= J2
y(n)W^
k
N
,
k = 0,1,...,mN-1
n=0
Since we have nonzero input values only at intervals of m, we can substitute
n = ran. Then, we get
JV-l iV-l
Y(k) = £ y(mn)W™Z
k
= £ y(mn)WR
k
= X(k mod N),
n=0 n=0
where k =
0,1,...,
mN
—
1. Y(k) can be obtained by repeating X(k) m
times.
This is due to the periodicity of Wfi
k
.
Example 4.32 Let m = 2 and x(n) =
{2,1,3,4}.
X{k) = {10,-1 +
j3,0,-l-j3}.
Then,
y(n) = {2,0,1,0,3,0,4,0}^
Y{k) = {10,-l+j3,0,-l-A10,-l+A0,-l-j3} I
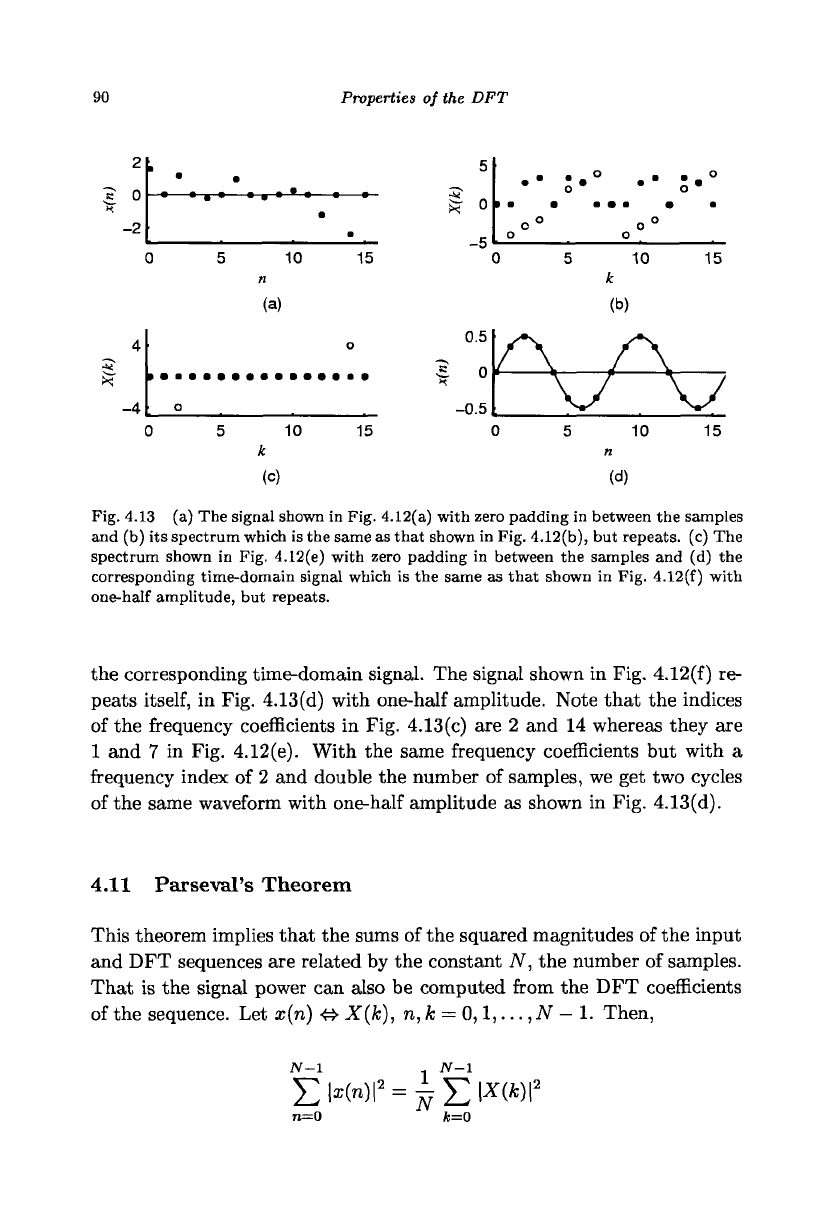
Figures 4.13(a) and (b) show, respectively, the signal in Fig. 4.12(a) padded
up with eight zeros placed in between the samples and the corresponding
spectrum. The spectrum shown in Fig. 4.12(b) repeats
itself,
in Fig. 4.13(b).
A similar effect is observed in padding with zeros in the frequency-
domain. Figures 4.13(c) and (d) show, respectively, the spectrum in
Fig. 4.12(e) padded up with eight zeros placed in between the samples and
90
Properties of the DFT
2
S o
H
-2
•
0
4
3~
X
-4
3
•
o
•
5
5
• • • •
•
10
n
(a)
10
k
(c)
•
15
o
15
5
sr
°
-5
• • •
o°
o
0 5
0.5
| 0
-0.5
/\
/ \
\
V
3 5
o . . o
• • • • •
0°
o
10 15
k
(b)
/\
/ \
/ \ /
/ \S
10 15
n
(d)
Fig. 4.13 (a) The signal shown in Fig. 4.12(a) with zero padding in between the samples
and (b) its spectrum which is the same as that shown in Fig. 4.12(b), but repeats, (c) The
spectrum shown in Fig. 4.12(e) with zero padding in between the samples and (d) the
corresponding time-domain signal which is the same as that shown in Fig. 4.12(f) with
one-half amplitude, but repeats.
the corresponding time-domain signal. The signal shown in Fig. 4.12(f) re-
peats
itself,
in Fig. 4.13(d) with one-half amplitude. Note that the indices
of the frequency coefficients in Fig. 4.13(c) are 2 and 14 whereas they are
1 and 7 in Fig. 4.12(e). With the same frequency coefficients but with a
frequency index of 2 and double the number of samples, we get two cycles
of the same waveform with one-half amplitude as shown in Fig. 4.13(d).
4.11 Parseval's Theorem
This theorem implies that the sums of the squared magnitudes of the input
and DFT sequences are related by the constant N, the number of samples.
That is the signal power can also be computed from the DFT coefficients
of the sequence. Let x(n) & X(k), n, k =
0,1,...,
N
—
1. Then,
JV-l iV-l
E wi
2
=
i E
i*(*)i
71=0
fc=0

Summary
91
Since the squared magnitude can be computed by multiplying a complex
number by its conjugate, we can write the left summation as
5>(n)|
2
=5>(n)z>)
n=0 n=0
Substituting the corresponding IDFT expressions for x(n) and x*(n) , we
get
JV-l JV-l JV-l
n=0 fc=0 m=0
N-lN-l
JV-l
= ^EE^*HE^
n(M
fc=0 m=0 n=0
If fe = m, this expression becomes
Otherwise, it evaluates to zero due to the orthogonal property.
Example 4.33 Consider the DFT pair
{2,1,4,3} O {10, -2 + j2, 2, -2 - j2}
The sum of the squared magnitude of the data sequence is 30 and that of
the DFT coefficients divided by 4 is also 30. I
The generalized form of this theorem applies for two different signals x(n)
and y(n) as given by
JV-l
1
JV-l
n=0 fc=0
4.12 Summary
• In this chapter, we have studied several properties of the DFT.
Either in applications of the DFT or in developing fast DFT algo-
rithms, these properties are repeatedly used. In the next chapter,
we shall find how the properties are used to develop fast DFT al-
gorithms.

92
Properties of the DFT
Reference
(1) Brigham, E. O. (1988) The Fast Fourier Transform and Its Appli-
cations, Prentice-Hall, New Jersey.
Exercises
4.1 Verify the linearity property ax{n) + by(n) & aX(k) + bY(k).
4.1.1 x(n) =
{2+j3,l-j4,2-j2,l+jl},y(n)
=
{2-j3,l-jl,2+j4,l-j2},
a = j3, and 6
=
2.
4.1.2 X(k)
=
{l-j4,2+j3,l-jl,2-j2}, Y(k)
=
{3
-
jl,4 +
jl,2
+
j2,1
+ j3}, a =
-j3,
and b = 4.
4.2 Verify the periodicity of the DFT and the IDFT.
* 4.2.1 Compute the DFT of x(n) = {1
-
j4,2 + j3,1
- jl,
2 +
j4}.
Find
X(23),
X(-47).
4.2.2 Compute the IDFT of X(k) = {2
-
jA, 2 + j2,1 + j5,1
- jl}.
Find
3(27),
x(-35).
4.3 Verify the time-domain shift property.
4.3.1 Find the DFT of x(n) = {2+jl, 1+J2, l-jl,4-j2}. Compute the
DFT of x(n + 3) using the shift property.
*4.3.2ThfiDFTofx(n-2)is{2 + j3,l-il,3-jl,2+j2}. Findx(n + 1)
using the shift property.
4.3.3 Compute the DFT of Ae~^e^
n
. Using the shift property, compute
theDFTof4e^'fe^("-
2
).
4.3.4 Compute the DFT of — 2sin(|7i). Using the shift property, compute
the DFT of -2 sin(f (n + 1)).
4.3.5 Let x(n)
=
{2,1,3,5,7,2,3,2,1,2,3}. Compute 4-point DFT of the
overlapping segments of x{n) with an overlap of 3 data values.
4.4 Verify the frequency-domain shift property.
4.4.1 Let x{n) = {1
-
jA, 2
-
j2,1
-
j3,2 + j5}. Find X(k). What is the
input that would generate the spectrum, (a) X(k
+
1). (b) X(k
—
1).
(c)
X(k-2).
4.4.2 Find the DFT of x(n)
=
{1
- jl,
2 +
jl,
1
-
j3,2 + j4}.
Deduce the spectrum of: (a) x(n) cos(^
L
n) and (b) x(n)sm(^n).
4.5 Compute the DFT of x(n) = {1
- jl,
2
-
j2,1 + j3,2
- jl}.
Deduce
the DFT of x (4
-n).

Exercises
93
4.6 Find the symmetry of x(n). Compute the DFT and verify that the
transform exhibits the anticipated property.
4.6.1 x(n)
=
{2,-4,2,-4}.
4.6.2 s(n)
=
{0,-3,0,3}.
* 4.6.3 x{n)
=
{-1,2,1,-2}.
4.6.4z(n)
=
{2,3,l,4}.
4.6.5z(n)
=
{l,2,3,2}.
4.7 Find the symmetry of x(n). Compute the DFT and verify that the
transform exhibits the anticipated property.
4.7.1 x(n) =
{-j4,-j2,j4,j2}.
* 4.7.2 x(n)
=
{0,-j4,0,j4}.
4.7.3 x(n)
=
{J2,j3,j2,
j3}.
4.7.4 z(n)
=
{jl,-j2,-j3,j4}.
4.7.5 x(n)
=
{-j2,jl,-j4,jl}.
4.8 Find the symmetry of x(n). Compute the DFT and verify that the
transform exhibits the anticipated property.
* 4.8.1 x(n) = {0,1
-
j2,0, -1 + j2}.
4.8.2 x(n) = {2 + j3,1
-
jl, -2
-
j3, -1 + jl}.
4.8.3 x(n)
=
{1 + j3,2 + j2,4
-
j3,2
-
jl}.
4.8.4 x{n) = {2 + j3,1 + j2, -2
-
j4,1 + j2}.
4.8.5 x{n)
=
{1
-
j2,2
-
j3,1
-
j2,2
-
j3}.
4.9 Find the DFT
of
x{n)
=
{0,1,1,0} and x{n)
=
{0,1,1,0,-1,-1}.
What are the number of nonzero frequency coefficients in each case.
4.10 Find the DFT of x{n)
=
{1
-
j4,2 + j3,1
-
jl, 3 +
j3}.
Deduce the
DFT of x*{n) and a;* (4
-
n)
4.11 Find, X(fc), the DFT of x(n)
=
{3+j3,2+j2,
l-j4,2-jl}.
Find the
DFT of: (a)
X(k)
and (b) X(4
-
k). What is the relation of the resulting
sequences to x(n).
* 4.12 Find the circular convolution of the time-domain sequences, x(n) —
{3,2,
-1,2} and h(n) =
{3,
-1,2,4} using the DFT.
4.13 Prove that the circular convolution of two frequency-domain sequences,
X(k) and H(k),
k =
0,1,...,
N-l
is
N
times the DFT of the product of the
corresponding time-domain sequences, x(n) and h(n),
n =
0,1,...,
N
—
1.
