Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

The Discrete Fourier Transform

loops,

the outer loop controlling the frequency index and the inner loop

controlling the access of the data values. In each iteration of the outer

loop,

one coefficient is computed. The real and imaginary parts of the

coefficients are stored, respectively, in arrays XR and XI, each of size N.

The access of correct twiddle factor values is carried out using the mod

function. Inside the inner loop, each coefficient is computed according to

the DFT definition. The next module, shown in Fig. 3.11(d), prints the real

and imaginary parts of the coefficients, respectively, from the arrays XR

and XI, one coefficient in each iteration. This module is called out-put.

3.5 Advantages of Sinusoidal Representation of Signals

The DFT is a tool to obtain the representation of a signal in terms of a set

of harmonically related discrete sinusoids. In general, a signal is represented

in other than its naturally occurring form to gain some advantages in sig-

nal processing and understanding. The sinusoidal representation of signals

is the predominant one when it comes to the analysis and design of LTI

systems because of the following advantages this representation provides.

(1) Efficient signal manipulation: When excited with a sinusoidal signal,

the output of a stable LTI system is a sinusoid of the same frequency as that

of the input. Therefore, the input and output are related only by a complex

constant, representing the amount of scaling of the amplitude and change in

the phase shift of the input signal. This is due to the fact that the derivative

and integral of a sinusoid is another sinusoid of the same frequency. This

characteristic along with the linearity and time-invariant properties of LTI

systems makes it efficient to implement fundamental operations such as

convolution. An arbitrary signal is represented as a sum of sinusoids and

the sum of the responses of a system to all the individual sinusoids is the

response to the arbitrary signal.

The frequency-domain representation provides a better understanding

of the signal characteristics.

In addition, a signal can be stored in a highly compressed form in the

frequency-domain representation because of the tendency of most practical

signals to have most of the energy concentrated in the lower part of the

spectrum.

(2) Availability of fast algorithms for the computation of the DFT: The

availability of fast algorithms for computing the DFT makes its use to

Advantages of Sinusoidal Representation of Signals

2.866

•£

1.134*1

0.5

-0.5

| 6.64

« 6.36

6.16

6.04

•

0.5

•

* R *

. § .

x(n)

(b)

•

1.5

(a)

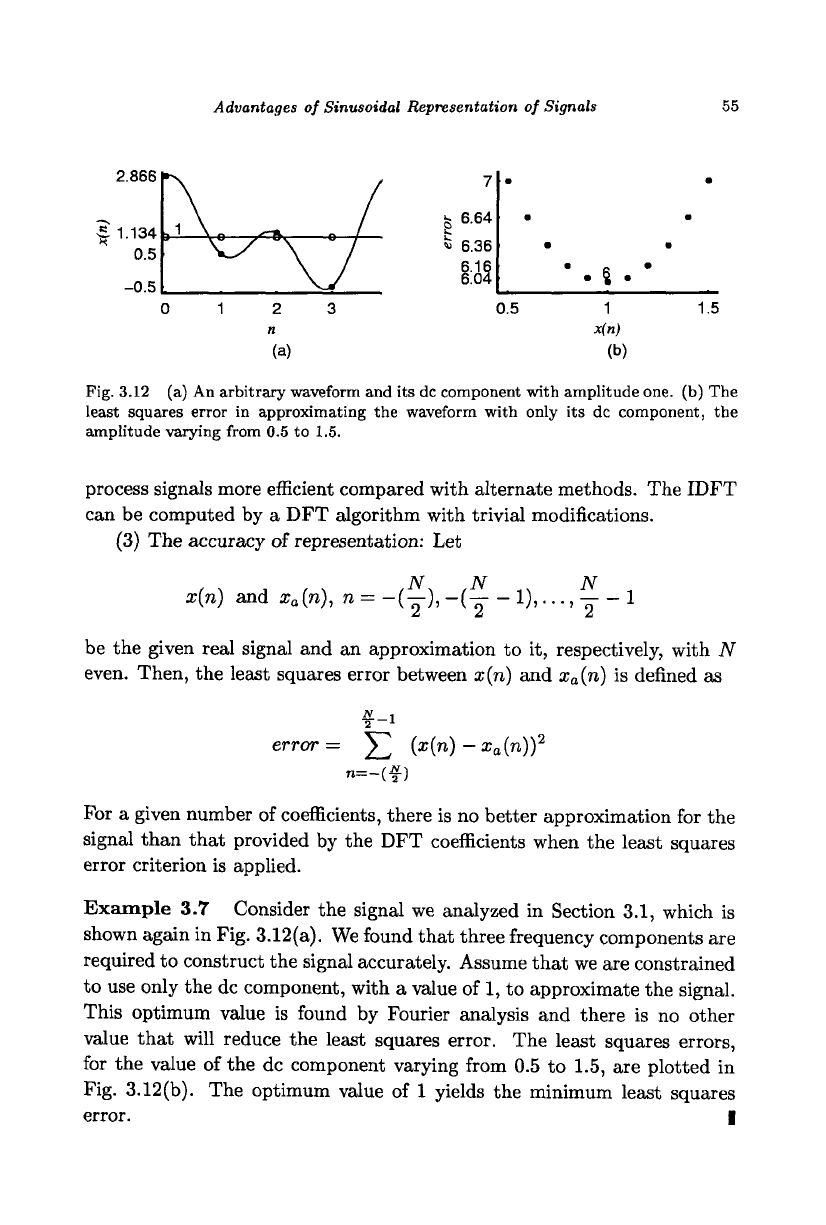
Fig. 3.12 (a) An arbitrary waveform and its dc component with amplitude one. (b) The

least squares error in approximating the waveform with only its dc component, the

amplitude varying from 0.5 to 1.5.

process signals more efficient compared with alternate methods. The IDFT

can be computed by a DFT algorithm with trivial modifications.

(3) The accuracy of representation: Let

N N N

x{n) and

{n),

n = -(—), -(— -

1),...,

— - 1

be the given real signal and an approximation to it, respectively, with N

even. Then, the least squares error between x(n) and x

(n) is defined as

error = ]P (x(n) -

(n))

For a given number of coefficients, there is no better approximation for the

signal than that provided by the DFT coefficients when the least squares

error criterion is applied.

Example 3.7 Consider the signal we analyzed in Section 3.1, which is

shown again in Fig. 3.12(a). We found that three frequency components are

required to construct the signal accurately. Assume that we are constrained

to use only the dc component, with a value of 1, to approximate the signal.

This optimum value is found by Fourier analysis and there is no other

value that will reduce the least squares error. The least squares errors,

for the value of the dc component varying from 0.5 to 1.5, are plotted in

Fig. 3.12(b). The optimum value of 1 yields the minimum least squares

error. I

56 The Discrete Fourier Transform

Let the signal x{n) be represented by N DFT coefficients exactly. Then,

-l

E *(Wv"*, n=-(^),-(^-l),...,£-l

*=-(f)

Let us approximate the signal x(ri) by x

(n) with M < N frequency

coef-

ficients

(k),

where M is odd (For convenience, we have put some con-

straints on the number of coefficients N and M. However, it should be

noted that this property is valid for any N and M.). Then,

M-l

°(

)

= jt E *«(*W**, n=-(y),-(y-l),...,y-l

In order to prove that the DFT provides coefficients with optimum val-

ues with respect to the least squares error criterion, we express the error

equation in a form so that the result is evident. Substituting for

(n),

get

SS-—1 M-l

errors £ (x(n) - 1 £ X

{k)W^

„=-(f) k=-(^i)

Expanding and rearranging, we get

= E *»-f E *»(*) E *(»w*

n=-(f) ^-(^i) «=-(f)

M-l M-l ^—1

+]J»

E E

*.(*>*.«

E ^

n(fc+,)

The second term is simplified by the fact that the summation involving n

X(—k).

The third term is simplified because the summation involving

the complex exponential is equal to N when I = —k and zero otherwise.

Therefore, we get

IV i M-l M-l

= E *»-;! E

Xa(k)X(-k)

+ ± J2 Xa(k)X

(-k)

„=-(f) *=-(^) *=-(^)

Advantages of Sinusoidal Representation of Signals

M-l

Adding and subtracting the term ^

YJ^III

M-I

)

X(k)X(-k) and using the

M-l M-l

fact that E^M^I) X

(fc)X(-fc) = E

fc=

(

}

*«(-*)*(*), we get

_j M-l

= E *»-^ E *(*)*(-*)

M-l

"4 E (X

(-k)X(k) + X

(k)X(-k)-X

(k)X

(-k)-X(k)X(-k))

Factoring the last term, we get

= E

a;2

(") + ^ E (X

(k)-X(k))(X

(-k)-X(-k))

n=-(f) *=-(^)

Af —1

-1 J2 X(k)X(-k)

Using the fact that the two expressions forming the product in the last two

terms are complex conjugates, we get

<¥._! M-l M-l

error = £ x

(n)+± £ \(X

(k)-X(k))f-± £ \X(k)f

The error is minimum only when X

(k) = X(k), since x{n) and X(fc) are

fixed. This implies that an optimal representation of a signal is provided

by the DFT coefficients with respect to the least squares error criterion.

When constrained to use only M < N coefficients to represent a signal,

the minimum error is obtained by using the M largest coefficients (not

necessarily the first M coefficients).

(4) The finality of coefficients: Because of the orthogonality property,

the coefficient value of a specific frequency component is independent of the

number of coefficients used to approximate a signal. This property allows

the computation of additional coefficients to improve the approximation of

a signal without the need to compute already found coefficients again.

(5) Representation of signal power: The signal power can be expressed

in terms of the frequency coefficients.

The Discrete Fourier Transform

(6) Complete representation: The least squares error in the approxi-

mation of a signal with the frequency coefficients can be made arbitrarily

small by increasing the number of coefficients.

(7) Conditions for existence: The sufficient conditions under which the

sinusoidal representation is possible are such that almost all signals of prac-

tical interest satisfy them.

3.6 Summary

• The DFT transforms an JV—point arbitrary time-domain sequence

into a set of JV frequency coefficients. The JV coefficients are the

representation of the given time-domain sequence in the frequency-

domain. These coefficients represent the magnitudes and phases (or

the amplitudes of cosine and sine components) of a set of harmon-

ically related sinusoidal sequences whose superposition summation

yields the time-domain sequence they represent.

• The representation of a finite length sequence in terms of infinite

length sinusoidal sequences is obtained by assuming that the finite

length sequence can be extended periodically.

• The IDFT transforms the JV frequency coefficients back into the

original set of JV time-domain samples by the process of superpo-

sition summation of the sinusoids represented by the JV frequency

coefficients.

• A signal is completely characterized either by the JV time-domain

samples or by the corresponding JV frequency coefficients.

• The representation of a signal by the DFT coefficients provides

minimum least squares error. In the next chapter, we study the

properties of the DFT.

References

(1) Guillemin, E. A. (1952) The Mathematics of Circuit Analysis, John

Wiley, New York.

(2) Cadzow, J. A. and Van Landingham, H. F. (1985) Signals, Systems,

and Transforms, Prentice-Hall, New Jersey.

Exercises

3.1 Formulate the Fourier analysis problem explicitly in terms of cosines

and sines. Find the coefBcients of sines and cosines for the waveform in

Fig. 3.1(d).

3.2 For the waveform shown in Fig. 3.1(d), verify the value of the coefficients

X(0),

X(2), and X(3) using Eq. (3.1).

3.3 For the waveform shown in Fig. 3.1(d), verify the value of the data

samples a;(0), x{2), and x(3) using Eq. (3.2).

3.4 Given the coefficients with N = 4, find the individual sinusoids. Note

that the coefficients are as defined by Eq. (3.3).

3.4.1 X(0) = -2,X(1) = 2v/2(l - jl),X(2) =

1,X(3)

= 2^2(1 +jl)

*3.4.2 X(0) =

1,X(1)

= 3(V3 + jl),X(2) = -1,X(3) = 3(V5 - jl)

3.4.3 X(0) = 3,X(1) = |(1 + jy/3),X{2) = -2,X(3) = |(1 - jy/i)

3.5 Write the DFT equation in matrix form with N = 8 showing the

numerical values of the twiddle factors.

3.6 Prove that the sum of the cosines, the frequency components of an

impulse signal, yields the impulse signal.

3.7 Derive the DFT of the dc signal, x{n) = 1, n =

0,1,...,

N - 1, from

the definition.

3.8 Find the DFT of

3.8.1 x(n) = 5{n - 2) with

= 8

*3.8.2 x(n) = 5{n + 2) with N = 8

3.9 Find the DFT of x(n) = (-1)" with N even.

3.10 Find the DFT of cos(fn) with N = 10 and N = 20.

*3.11 Find the DFT of x{n) = 3

-^"+f) with N = 16.

3.12 Find the DFT of 2sin(^n + |) with

= 16.

*3.13 Find the DFT of x{n) = e~

, n =

0,1,...,

N - 1, where (J is a

constant.

3.14 Find the DFT of x(n) = %,n =

0,1,..

.,N - 1.

The Discrete Fourier Transform

3.15 Find the IDFT of

3.15.1 X(k) = 3, 0 < k < 4.

3.15.2 X(0) = 8 and X(k) = 0 otherwise, 0 < k < 4.

3.15.3 X(3) = 26 and X{k) = 0 otherwise, 0 < k < 16.

3.15.4 X(2) = (| +

j&),

X(U) = {\ - j&), and X(k) = 0 otherwise, 0 <

A;<16.

* 3.15.5 X(5) = (-^ - j^), X(ll) = (-^ + j^), and X(fc) = 0

otherwise, 0 < k < 16.

3.15.6 X{5) = 4, X(ll) = 4, and X(fc) = 0 otherwise, 0 <

< 16.

3.15.7 X(10) = 8, X(22) = 8, and X(k) = 0 otherwise, 0 < k < 32.

3.15.8 X(3) = -j8, X(13) = j8, and X(k) = 0 otherwise, 0 < k < 16.

3.15.9 X(2) = -;5 and X(k) = 0 otherwise, 0 < Jb < 16.

3.16 Compute the DFT. Verify the transform pair by computing the IDFT

of the transform to get back x(n).

3.16.1 x(n) = {3,2,1,-4}

3.16.2 x{n) = {2 + j3,10 + j2, -4 + jl, 6 - j4}

3.17 Find the 4-point DFT of x(-2) = l,a:(-l) = -4,a;(0) = 3,a;(l) = 2

using the center-zero format of the DFT. Using the center-zero format of the

IDFT, verify the transform pair by computing the IDFT of the transform

to get back x(n).

Programming Exercises

3.1 Write a program for the direct implementation of the DFT.

3.2 Write a program for the direct implementation of the IDFT.

Chapter 4

Properties of the DFT

In this chapter, we study the properties of the DFT. The existence of advan-

tageous properties is the major reason for the widespread use of the DFT.

In applications of the DFT or in deriving DFT algorithms, the properties

are repeatedly used.

4.1 Linearity

The linearity property implies that the DFT of a linear combination of

a number of signals is the same linear combination of the DFTs of the

individual signals. Let X(k) and Y(k), respectively, be the DFT of x(n)

and y(n). It is assumed that the lengths of the sequences x(n) and y(n)

are equal. If the sequences are not of equal length, they are assumed to be

appended by sufficient number of zeros so that their lengths become equal.

The DFT of ax(n) + by{ri), where a and b are real or complex constants, is

given by

N-l

Y,(ax(n)

+ by(n))WZ

Due to the linearity property of the summation operation, we can rewrite

this equation as

N-l

a ^

x(n)WH

+ b Y^ y(n)W$

= aX(k) + bY(k)

n=0 n=0

That is, ax(n) + by{n)

<s>

aX(k) + bY(k).

Properties of the DFT

Example 4.1 Let a = 1, 6 =

x(n) =

{1,2,1,3},

and y(n) =

{2,1,1,4}.

X(fc) =

{7,

-3, -j} and Y(fc) = {8,1 + j3, -2,1 - j3}. Then, the DFT

<rfar(n)+jj/(n) = {1 + j2,2 + jl,l + jl,3 + j4} is X(k) + jY{k) = {7 +

j8,-3+j2,-3-j2,3 + j0}. I

Linearity applies in both the time- and frequency-domains.

4.2 Periodicity

A sequence x(n) is denned periodic with period N if x(n) = x(n + aN),

where a is any integer. In DFT analysis, both the input data and its

DFT are assumed periodic of period N, the length of the sequence. This

property follows from the fact that the discrete complex exponential, W£

is periodic with a period N. By substituting k + aN for k in Eq. (3.6), we

get

JV-l N-l

X(k + aN)=Yl x(n)W$

k+aN)

= £

x[n)W%

= X(k),

n=0 rc=0

where k =

0,1,...

—

Similarly, by substituting n+aN for n in Eq. (3.7),

we get

x(n + aN) = 1 £

X(k)W^

n+aN)k

= 1 £ X(fe)^"

= *(«),

fc=0 fc=0

where n =

0,1,...

—

1. The periodicity of x(n) and X(fc) with a period

of 8 is shown in Fig. 4.1.

Example 4.2 Consider the DFT pair

x(n) = {2+jl,3+j2,l-jl,2-j3}&X(k) = {8-jl,6+jl,-2+jl,-4+j3}

Now, x(4) = x(0) = 2 + jl and X(-l) = X(3) = -4 +

j3.

4.3 Circular Shift of a Time Sequence

Consider the sequence, x(n) = {x(0),x(l),x(2),x(3),x(4),x(5),x(6),x(7)},

shown in Fig. 4.1. The circular shift of the sequence to get x(n - 1) =

{x(7),

x(0), x(l), x(2), x(3), x(4), x(5), x(6)} means the rotation of the circle

by one position in the counterclockwise direction as shown in Fig. 4.2. The

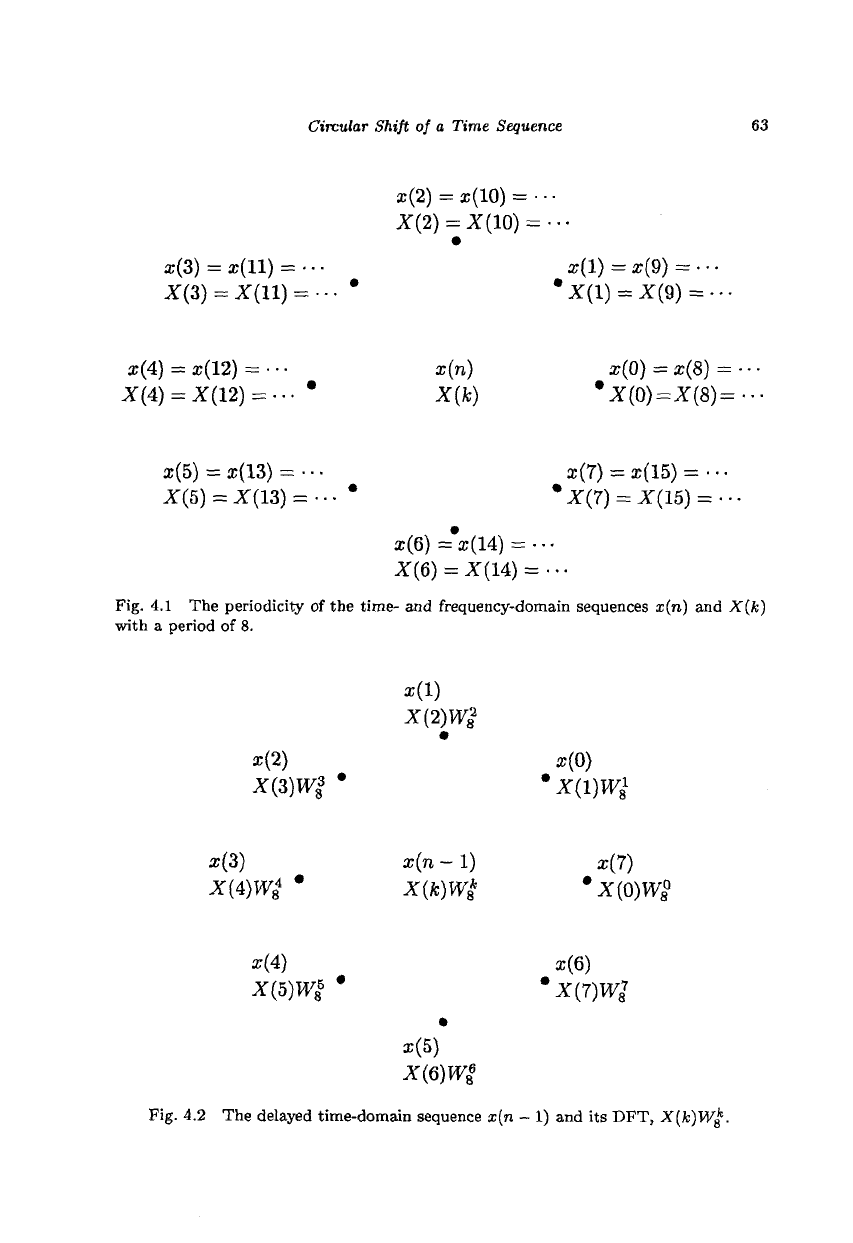
Circular Shift of a Time Sequence 63

x(3) = x(ll) =

• • •

X(3) = X(11) = --- '

x(4) = se(12) =

• • •

X(4) = X(12) = --- *

x(2) = ar(10) = •

X{2) = X{10) =

•

x{n)

X(k)

x{5) = ar(13) =

• • •

X(S) = X{13) = ••• *

x(6) =x(U) = •

X(6) = X(U) =

x(l) = x(9) = •••

*X(1) = X(9) = -

x(0) = ar(8)

*X(Q)=X(8)

x(7) = x(15) =

• •

*X(7) = X(15) =

Fig. 4.1 The periodicity of the time- and frequency-domain sequences x(n) and X(k)

with a period of 8.

x{2)

X(3)W$ *

*(3)

X(4)W$ *

ar(4)

X(5)W

5 #

x(l)

X(2)Wi

•

a;(n - 1)

X{k)Wg

•

X{G)W$

x(0)

x(7)

*X(0)W$

1(6)

*X(7)W

Fig. 4.2 The delayed time-domain sequence x(n - 1) and its DFT, X{k)w£.