Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

The Discrete Fourier Transform

x(n) = 1 + cos(f n - f) + cos(7rn)

x(n) = cos(nn)

x(n) = cos(|n - |)

• • • •

(a)

x(n) = 1

(b)

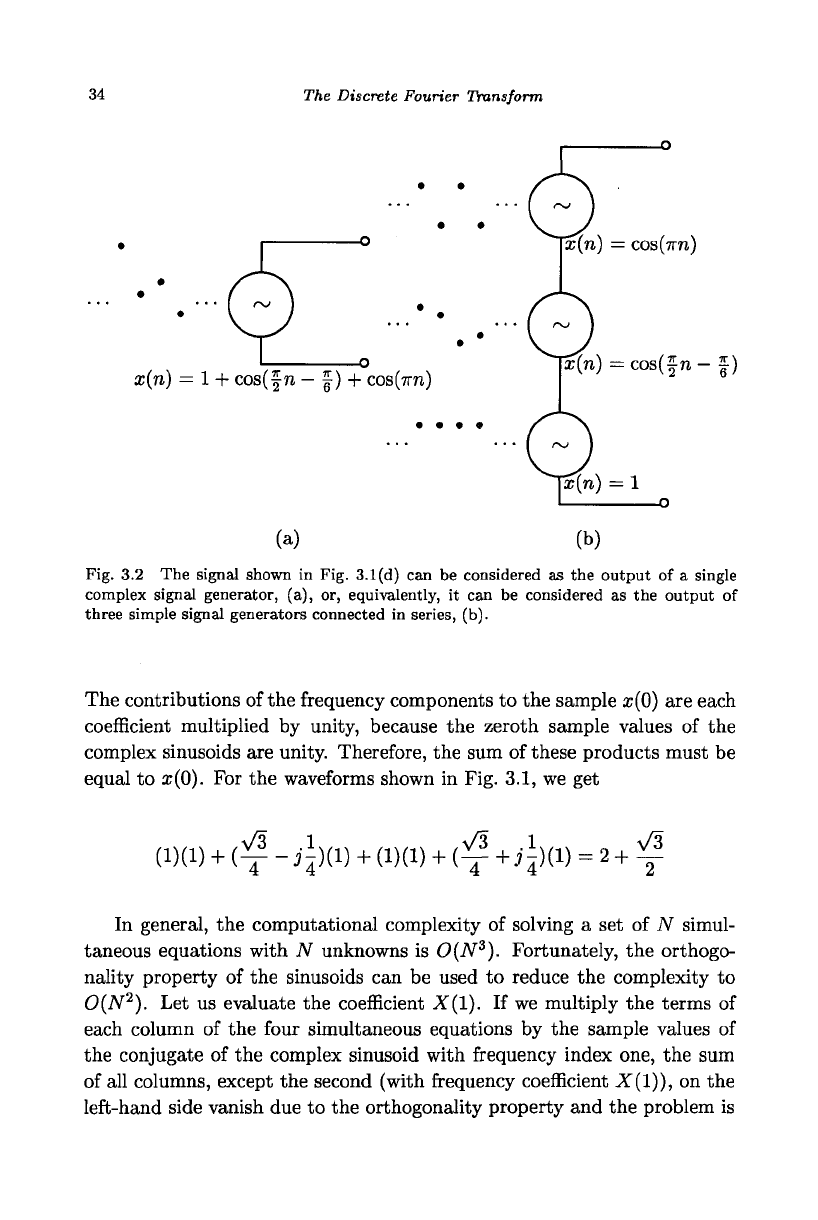
Fig. 3.2 The signal shown in Fig. 3.1(d) can be considered as the output of a single

complex signal generator, (a), or, equivalently, it can be considered as the output of

three simple signal generators connected in series, (b).

The contributions of the frequency components to the sample x{0) are each

coefficient multiplied by unity, because the zeroth sample values of the

complex sinusoids are unity. Therefore, the sum of these products must be

equal to x(0). For the waveforms shown in Fig. 3.1, we get

(i)(i) + (^ - ji)(i) + (i)(i) + (^ +;l)(i) =

+ ^

In general, the computational complexity of solving a set of N simul-

taneous equations with N unknowns is

0(N

Fortunately, the orthogo-

nality property of the sinusoids can be used to reduce the complexity to

0(N

Let us evaluate the coefficient X(l). If we multiply the terms of

each column of the four simultaneous equations by the sample values of

the conjugate of the complex sinusoid with frequency index one, the sum

of all columns, except the second (with frequency coefficient -X"(l)), on the

left-hand side vanish due to the orthogonality property and the problem is

The Fourier Analysis and Synthesis of Waveforms 35

reduced to summing the following two columns.

jr(l)eW>)(i)

-^(°)W = z(0)e-''T(°)(i)

X(l)eiT(DW

-iT(i)(i) = xtfe-*

?™

)

X(l)e^(2)(i)

-i¥(2)(i) = o;(2)e-^(2)(i)

X(l)e^(3)(D

-i¥(3)(i) = a:(3)

-^(3)(i)

The result of summing these equations is given by

a(l) = i(0)e-^(»)W+i(l)e-^(

)W+x(2)e-^(

)(

)+i(3)e-^(

)(

)

Substituting specific values, we see that the equation is satisfied.

(2 + ^)(1) + (l)(-j) + (2 - ^)(-l) + (-I)O-) = V3-jl = 4X(1)

Now, we can deduce a formula that can be used to compute any of the four

frequency coefficients.

X(k) = -Y,<n)e-^

, fc = 0,l,2,3 (3.1)

n=0

The Fourier synthesis of waveforms

The four equations set up for the analysis problem constitute the synthesis

of the waveform from the coefficients. However, it is instructive to develop

the synthesis problem formulation independently. Due to the orthogonality

property, multiplying the sample values of an arbitrary waveform by the

corresponding sample values of the conjugate of the complex sinusoid at

a frequency and summing the products must be equal to the coefficient of

that frequency component with a scale factor N, the number of samples

(for the present example N = 4). Therefore, we set up four simultaneous

equations with four frequency coefficients.

a:(0)e-^(°)(°) +ar(l)e-^<°X

) +z(2)

-^(°K

) +ar(3)e-^(°)(

> = 4X(0)

a;(0)e-^ WW+x(l)e-^(

)(

)+x(2)e-^W(2)

+a;

(3)

-^(i)(3)

4X(l)

a;(0)e-^T(2)(o)

-^(2)(i)

+a;(

-^(2)(2)

(3)e

-j^

(2)(3)

= 4X(2)

x(0)e^'"(

)(°)+a

;

(l)e-^(3)(i)

+a;

(2)

-i¥(3)(2)

+a;

(3)

-^(3)(3)

)

The contributions of the data samples to the coefficient X(0) is each data

sample multiplied by unity, because the sample values of the conjugate of

the complex sinusoid with frequency index zero are unity. Therefore, the

The Discrete Fourier Transform

sum of these products must be equal to AX

(0).

For the waveform shown in

Fig. 3.1, we get

(2 + ^)(1) +

(\)(1)

+ (2 - ^)(1) +

(-!)(!)

= 4(1)

Let us evaluate the time-domain sample a;(l). If we multiply the terms

of each column of the four simultaneous equations by the sample values with

index 1 of the complex sinusoids, the sum of all columns, except the second

(with data sample x(l)), on the left-hand side vanish due to orthogonality

property and the problem is reduced to summing the following two columns.

ar(l)e-^(o)(iV¥(°)(i) = 4X(0)e^(o)(i)

a;(l)e-^(i)(i)e^(i)(i) = 4X(l)e^(i)W

^lJe-^eWVTPXi) = 4X(2)e^(

)(

)

i(l)e-'T(3)W

iT(3)W = 4Y(3)e*T(3)(i)

The result of summing these equations is given by

4ar(l) = 4(I(0)e^T(»)(i) +X(l)e^W +X(2)e^(2)W +X(3)e^(

)M)

Substituting specific values for the example, we see that the equation is

satisfied.

x(i) = (i)(i) + (i(V5 - ji))U) + (i)(-i) + (\(V3 + ji))(-j) = \

Now, we can deduce a formula that can be used to compute any of the four

time-domain samples.

x(n) = ^X(ifc)e

'T"*,

= 0,1,2,3 (3.2)

Jfe=0

The DFT and IDFT expressions

Equations 3.1 and 3.2, respectively, are the mathematical formulations of

the Fourier analysis and synthesis problems using harmonically related dis-

crete sinusoids as the basis functions. All that is to be said is about some

conventions. The division operation in Eq. (3.1) can be shifted to Eq. (3.2).

The complex exponential can be written in a more compact form using the

abbreviation Wi = e

^. With these observations, the analysis equation

The DFT and the IDFT

becomes

X{k) = ^x{n)WZ

, ft = 0,1,2,3 (3.3)

n=0

and the synthesis equation becomes

ar(n) =

5]jr(*)W7

*, n = 0,l,2,3 (3.4)

k=o

These two equations, called, respectively, DFT and IDFT, are a transform

pair. What one does the other undoes. In the literature, one can find some

variations in the definitions and a particular variation must be consistently

used.

The frequency composition of real signals

Although we use complex sinusoids in the problem formulation, for real

signals, the complex sinusoids combine to yield a real signal. For the present

example, expanding Eq. (3.4), we get

-, i

x(n) = ±{X(0) + ^2(X(k)Wr

" + X(4 - fc)W

fc)

) +

X(2)W

"},

fc=i

= J{X(0) + 2|X(l)| cos(|n + /.X(1)) + X{2) cos(Trn)}, n = 0,1,2,3

In general, we get

x(n) = ±{X(0) + 2 J2 {\X(k)\ co

(^nk + ZX(fe))) + X(j) cos(Trn)},

where n =

0,1,...,

—

1. Therefore, an iV-point real signal, where iV is

even, is composed of ^ +1 sinusoidal waveforms.

3.2 The DFT and the IDFT

In this section, we examine the DFT and IDFT expressions in detail. A

bandlimited periodic time-domain sequence x(n), with period N, can be

represented in terms of a summation of a set of N harmonically related

The Discrete Fourier Transform

complex sinusoids with coefficients X(k) as

JV-l

x(n) = J2 X(k)e

, n =

0,1,..

.,N - 1 (3.5)

fc=o

In order to evaluate a specific coefficient X(k) in terms of x(n), we replace

the index k by m on the right side of Eq. (3.5) (We use a dummy variable to

avoid confusion between two independent frequency-domain variables. Note

that similar substitutions will be made in other derivations.), multiply both

sides of the nth equation by e~i~R~

, and sum them over the interval n = 0

to n = N

—

1. This process yields, for a specific k,

N-l

N-l N-l

n—0 m=0

N-l

(

)

n(m

fc)

NX(k)

71=0 71=0 771=0

7V-1 JV-l

771=0 71=0

with the fact that

N-l

for m / k

j%-n(m-k)

f N for m = k

7J=0

(Summations of complex exponential terms similar to the inner summation

and the evaluation of the outer summation will occur several times in the

proofs of DFT properties that the reader is well advised to get thoroughly

familiar with it.) Therefore, we get

X(k) = ^x(n)e-^

71=0

The constant factor ^ is usually suppressed and the iV-point DFT of the

sequence x(n) is defined as

N-l

X{k)=J2

(

)

> fc = 0,l,...,iV-l (3.6)

71=0

The DFT and the IDFT

x(n) = 1+ cos(f n - f) + cos(7rn)

ra)

(

] 1 2

0 12

a:(n) = l ...••••

a:(n)=cos(fn-f)...-^.

x(n) = cos(7rn)

(b)

x{n) = cos(7rn)

x(n) = cos(f n - f)

x(n) = 1

(a)

summing

unit

x(n) = 1 + cosff n

—

+ cos(7rn)

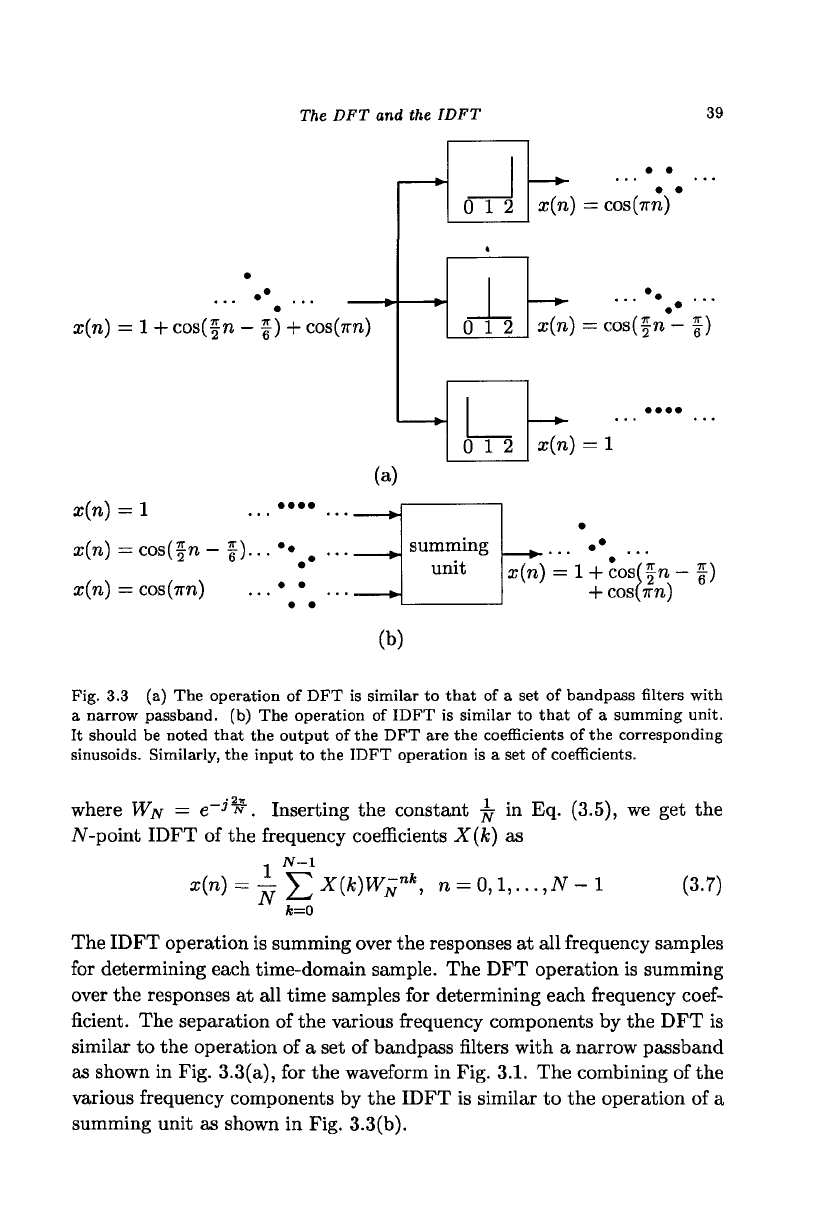
Fig. 3.3 (a) The operation of DFT is similar to that of a set of bandpass filters with

a narrow passband. (b) The operation of IDFT is similar to that of a summing unit.

It should be noted that the output of the DFT are the coefficients of the corresponding

sinusoids. Similarly, the input to the IDFT operation is a set of coefficients.

where WN = e

'« . Inserting the constant ^ in Eq. (3.5), we get the

iV-point IDFT of the frequency coefficients X(k) as

7V_1

i(n) = -^X(i)V, n = 0,l,...,AT-l (3.7)

The IDFT operation is summing over the responses at all frequency samples

for determining each time-domain sample. The DFT operation is summing

over the responses at all time samples for determining each frequency

coef-

ficient. The separation of the various frequency components by the DFT is

similar to the operation of a set of bandpass filters with a narrow passband

as shown in Fig. 3.3(a), for the waveform in Fig. 3.1. The combining of the

various frequency components by the IDFT is similar to the operation of a

summing unit as shown in Fig. 3.3(b).

The Discrete Fourier Transform

It can be verified that Eqs. (3.6) and (3.7) form a transform pair. Sub-

stituting for X(k) in the ID FT definition, we get

fc=0 ro=0

Changing the order of summation, we get

m=0 Jfe=0

Since the inner summation evaluates to N for m — n and zero otherwise,

the expression on the right-hand side is equal to x{n) and the transform

relationship is established.

For N = 8, we have shown the cosine and sine components of the DFT

basis functions

Xk(n) =

= cos(-nk) + jsin(—

nk),

n,k = 0,1,...,N

—

in Fig. 3.4. The sample values of sines and cosines used in DFT for evalu-

ating frequency coefficients are represented compactly by the complex ex-

ponential and the notation used is Wfi

= cos(^nfc)

—

j sin(^nA;), called

the twiddle factor. The sine function of the twiddle factor is the negative

of that shown in Fig. 3.4 because of the conjugation of the basis function.

Note that, from the sample values of the fundamental shown in Fig. 3.4(b),

the sample values of the other waveforms in Fig. 3.4 can be easily deduced

as the waveforms are harmonically related.

The discrete complex exponential is a periodic function of nk with a pe-

riod N. Therefore, the twiddle factors are periodic, as shown in Fig. 3.5 for

N = 8. They are iVth roots of unity. The roots of unity are called twiddle

factors, because multiplying a number by a twiddle factor is changing the

phase of that number or rotating a vector without changing its magnitude.

Frequencies, called DFT bins, at which the spectral values are computed

are also shown in Fig. 3.5. For example, the point marked 0 corresponds

to dc, that is / = 0. The point marked | corresponds to the fundamental

frequency f = h cycles per sample. This is also the frequency increment of

the DFT spectrum.

The DFT and the IDFT

I e—e—e——e—e—o o—e-

* -1

(a)

r^z^^

\ o

-. 1

^ o

p^?

* S

•cc^r^

\/7

^^i^.^^"

«_-^*^-_o

-®^^

4 6

(b)

**P7/7C\

\5G/

(c)

(d)

jfy/VW »;Ry?^*^

(e)

i^QxC^ >0*C-^

(f)

(g)

(h)

Fig. 3.4 The cosine and sine components of the DFT basis functions, with N = 8 and

frequency indices varying from 0 to 4, are shown, respectively, in (a), (b), (c), (d), and

(e).

Note that (f), (g), and (h) are, respectively, the same for cosine and the negative

for sine as that of (d), (c), and (b). This duplication is due to the use of complex

exponentials in the DFT problem formulation. The sine function with frequency indices

0 and 4 have all sample values equal to zero.

Half-wave symmetry of the DFT kernel matrix

The DFT equation, with N = 8, is denned as

*(fc) = 5>(n)W

"*, fc =

0,l,...,7

n=0

Writing the eight individual equations, we get

X(0) = x(0)Wg + x(l)Wg + x(2)W° + z(3)W° + a;(4)W

+ x(5)Wg

+ x(6)W

° +x(7)Wg

X(l) = x(0)W° + x{l)Wl +

x(2)W*

+ x(3)W$ + x(4)W

+ x(5)W

+ x(6)Wg +z(7)W

The Discrete Fourier Transform

8 8" "

= --- ,i w?

w§

= wi =

---

o g o

Fig. 3.5 The periodicity of the twiddle factors, with N = 8, and the discrete frequencies

at which the spectral values are computed.

X(2) = x(0)Wg +x(l)W£ + x(2)W£ +

x(3)W*

+ ar(4)W| + x(5)W

+ x(6)W^+x(7)W^

X(3) = x{0)Wg + x(l)W$ + x(2)W£ + x(S)Wg + z(4)W

+ x(5)W

x{6)W^

+ x{7)W£

JT(4) = s(0)W

° + x(l)W£ + x{2)Wi + x(3)W

+ z(4)W

+ x(5)W

+ x(6)W|

+ x(7)W£

X(5) = x(0)W° + x(l)Wi + x{2)W™ + x(3)W£

+ x{4)Wg° + x(5)W£

+ x(Q)Wi° + x(7)Wi

X(6) = z(0)W

° + x(l)W

+ x(2)W

+ x(3)W

+ x(4)W

+ x(5)W|°

+ x(6)W

+ x(7)W

X(7) = x(0)W°

x(l)W

+ x(2)W

+ z(3)W

+ x(4)W

+ x(5)W

+ x(6)W

+ x(7)W$

The even-indexed sines and cosines of the twiddle factors complete an even

number of cycles. Therefore, they are even half-wave symmetric, x{n) =

x(n ± y). At n = y, we start getting the first-half sample values since

they start a new cycle.

cos(^(2fc)(n±y)) = cos(~2kn) and sin(-^(2ft)(n±y)) = sin(-^2fcn)

The DFT and the IDFT

Since the odd-indexed sines and cosines complete an odd number of cycles,

they are odd half-wave symmetric, x(n) = —x{n ±

T£).

At n = %, we start

getting the first-half sample values with sign reversed since they start the

second half of a cycle.

cos(-^(A)(n±y)) = -cos(—kn) and sin(—(k)(n±—)) •sin —«n)

The waveforms shown in Fig. 3.4 exhibit this property. The samples of all

the waveforms at a sample point also exhibit this same half-wave symmetry

property. Therefore, the twiddle factor matrix is symmetric. The DFT

equations can be rewritten showing the half-wave symmetry explicitly, using

matrices, as

X(0)1

X(l)

X(2)

X(3)

X(4)

X(5)

X(6)

X(7) .

° W

° Wi W

° W

^8° Ws

W£ Wi -Wg -Wg

-Wi -W$

w$ wi wi w§ w§ wi wi wi

wi wi wi wi -wi -wi -wi -wi

wi -wi wi -wi wi -wi wi -wi

-w^

wi -wi -wi

w£

-wi wi

wi -wi wi -wi wi -wi wi -wi

wi -wi wi -wi -wi wi -wi wi

• x(0)

x(l)

x{2)

x(3)

x{4)

x(5)

x(6)

*(7)

The twiddle factor matrix is called the kernel matrix of the DFT. Exploiting

the symmetry, as will be seen in Chapter 5, this equation can be written

more compactly. Note that, in the DFT definition, the time-domain index

starts from zero. It does not necessarily mean that the signal always start

from zeroth instant. Since periodicity is implied in computing the DFT,

we can always get the time-domain samples starting from the index zero.

Of course, we can also change the limits of the summation as orthogonality

of complex exponentials holds for any interval of N samples. A particular

case of interest is described below.

Center-zero format of the DFT and IDFT

With N even, the DFT and IDFT expressions are sometimes written as

--i

N N IV

(3.8)

X(k)= Y, *(«)W^*.

= -(T)'-(f-

)'•••'?-

n=(-f)