Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

Introduction

Discrete Fourier Transform, the theory and properties of the 2-D DFT

is presented. The practically efficient way of computing the 2-D DFT is to

compute the row DFTs followed by the computation of the column DFTs

and vice versa. Using this approach, the 2-D PM DFT algorithms are

derived.

In practice, most of the naturally occurring signals are continuous-time

signals. It is by representing this signal by a set of finite samples, we

are able to use the DFT. This creation of a set of samples to represent

a continuous-time signal necessitates sampling and truncation operations.

These operations introduce some errors in the signal representation but,

fortunately, these errors can be reduced to a desired level by using an ap-

propriate number of samples of the signal taken over proper record length.

Therefore, the level of truncation and the number of samples used are a

trade-off between accuracy and computational effort. A good understand-

ing of the effects of truncation and sampling is essential in order to analyze

a signal with minimum computational effort while meeting the required ac-

curacy level. In Chapter 11, Aliasing and Other Effects, the problems

created by sampling and truncation operations, namely aliasing, leakage,

and picket-fence effects, are discussed.

The continuous-time Fourier series (FS) is the frequency-domain repre-

sentation of a periodic continuous-time signal by an infinite set of harmon-

ically related sinusoids. In Chapter 12, The Continuous-Time Fourier

Series, the approximation of the continuous-time Fourier Series, 1-D and

2-D, by the DFT coefficients is described. The inability of the Fourier rep-

resentation to provide uniform convergence in the vicinity of a discontinuity

of a signal is also discussed. The continuous-time Fourier transform (FT) is

the frequency-domain representation of an aperiodic continuous-time signal

by an infinite set of sinusoids with continuum of frequencies. In Chapter 13,

The Continuous-Time Fourier Transform, the approximation of the

samples of the continuous-time Fourier transform, 1-D and 2-D, by the

DFT coefficients is described.

A major application of the DFT is the fast implementation of fundamen-

tally important operations such as convolution and correlation. In Chap-

ter 14, Convolution and Correlation, the fast implementation of the

convolution and correlation operations, 1-D and 2-D, using the DFT is

presented.

The even extension of a signal eliminates discontinuity at the edges,

if present, thereby enabling the signal to be represented by a smaller set

The Organization of this Book 5

of DFT coefficients. This special case of the DFT is called the discrete

cosine transform and it is widely used in practice for signal compression. In

Chapter 15, Discrete Cosine Transform, the computation of the discrete

cosine transform, 1-D and 2-D, is presented.

While the sinusoids are the basis waveforms in the DFT representation

signals,

a set of orthogonal rectangular waveforms is used to represent sig-

nals in the discrete Walsh-Hadamard transforms. These transforms, often

used in image processing, are computationally efficient since only addition

operations are required for their implementation. Algorithms for their com-

putations are very similar to those of the DFT algorithms. The study of

these transforms provides a contrast in representing an arbitrary waveform

using a different set of orthogonal waveforms. In Chapter 16, Discrete

Walsh-Hadamard Transform, the computation of the discrete Walsh-

Hadamard transforms, 1-D and 2-D, is described.

In the Appendices, the complex numbers, the measure of computational

complexity, the bit-reversal algorithm, the prime-factor DFT algorithm for

a data size of six, and the testing of programs are briefly described. A list

of useful mathematical formulas is also given.

The theory of the Fourier analysis is that any periodic signal satisfying

certain conditions, which are met by most signals of practical interest, can

be represented uniquely as the sum of a constant value and an infinite

number of sinusoids with frequencies those are integral multiples of the

frequency of the signal under analysis. In short, almost everything that is

said in this book is concerned with this one line.

Chapter 2

The Discrete Sinusoid

A signal represents some information. Manipulation of signals, such as

removing noise from a signal, is a major activity in applications in science

and engineering. An arbitrary signal can be easily manipulated only by

representing it as a linear combination of simple and mathematically well-

defined signals. There are many ways a signal can be represented. The

proper representation of a signal is crucial for the efficient manipulation

of it. For the analysis and design of LTI systems, most often, signals are

represented as a linear combination of the impulse signal in the time-domain

and the sinusoidal signal in the frequency-domain.

In Sec. 2.1, we briefly describe the time- and frequency-domain repre-

sentations of signals. The sinusoidal waveform is the principal object in

Fourier analysis. In Sec. 2.2, we study the characteristics of the discrete

sinusoidal waveform and its representation by complex exponentials. The

orthogonality property of the sinusoids is also presented.

2.1 Signal Representation

Time-domain signal representation

Signals occur, mostly, in a form that is called the time-domain represen-

tation. In this form, the signal amplitude, x(t), is represented against

time,

t. If the signal is denned at all instants of time, it is referred as a

continuous-time or analog signal. If the signal is defined only at discrete

instants of time, then the signal is referred as a discrete signal. It is as-

sumed that the interval between instants of time is uniform. Figures 2.1(a)

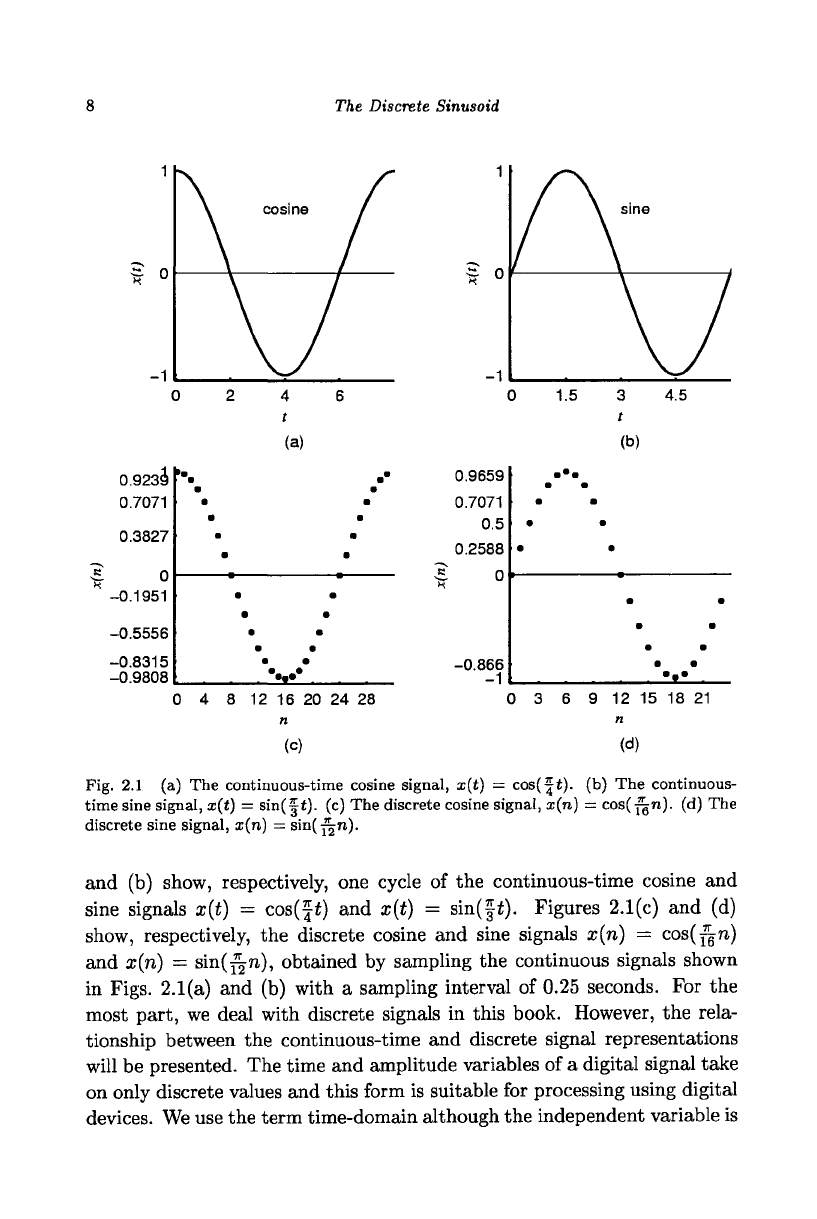
The Discrete Sinusoid

0.9239

0.7071

0.3827

-0.1951

-0.5556

-0.8315

-0.9808

(a)

(b)

0.9659

0.7071

0.5

0.2588

-0.866

-1

0 4 8 12 16 20 24 28

(c)

0 3 6 9 12 15 18 21

(d)

Fig. 2.1 (a) The continuous-time cosine signal, x{t) = cos(f

t).

(b) The continuous

time sine signal, x(t) = sin(|t). (c) The discrete cosine signal, x(n) = cos( f^n). (d) Thi

discrete sine signal, x(n) = sin(y^n).

The

and (b) show, respectively, one cycle of the continuous-time cosine and

sine signals x(t) = cos(ft) and x{t) = sin(ft). Figures 2.1(c) and (d)

show, respectively, the discrete cosine and sine signals x(n) = cos(f^n)

and x(n) — sin(^n), obtained by sampling the continuous signals shown

in Figs. 2.1(a) and (b) with a sampling interval of 0.25 seconds. For the

most part, we deal with discrete signals in this book. However, the rela-

tionship between the continuous-time and discrete signal representations

will be presented. The time and amplitude variables of a digital signal take

on only discrete values and this form is suitable for processing using digital

devices. We use the term time-domain although the independent variable is

Signal Representation

not time for all the signals. For example, in a speech signal, the amplitude

of the signal varies with time whereas the intensity values of an image vary

with two spatial coordinates. Signals such as speech signal, which vary

with respect to a single independent variable, is called a one-dimensional

(1-D) signal. An image is a two-dimensional (2-D) signal since it varies

with respect to two independent variables.

A discrete signal is represented, mathematically, as a sequence of num-

bers {x(n), —oo < n < oo}, where the independent variable n is an integer

and x(n) denotes the nth element of the sequence. Although it is not

strictly correct, x{n) is also used to refer a sequence as the sequence x(n).

The element x(n) of a sequence is often referred as the nth sample of the

sequence regardless of the way the sequence is obtained. Usually, a dis-

crete sequence is obtained by sampling an analog signal. However, discrete

signals can also be generated directly. Even if the signal is obtained by

sampling a continuous-time signal, the sampling instant is shown explicitly

only when it is required as x(nT

), where T

is the sampling interval.

The unit-impulse signal, shown in Fig. 2.2(a), is defined as

, . ( 1 for n = 0

(B) =

\ 0 forn^O

In practice, the input signal to a system, most often, is quite arbitrary and

it is difficult to represent and manipulate it analytically. To circumvent this

problem, it is a necessity to represent the signal as a linear combination of

elementary signals. An arbitrary signal can be represented as the sum of

delayed and scaled unit-impulses. An arbitrary discrete signal, {x(—1) =

-l,x(0) = l,ar(l) = -3,z(2) = 2}, is shown in Fig. 2.2(b). This signal can

be expressed as

(

)

(

)ti(n-™>)

or x

(

) = -6(n+l)+6(n)-36(n-l)+26(n-2)

m=—1

and the constituent impulses are shown in Figs. 2.2(c) to (f). With this

type of representation, if the unit-impulse response of an LTI system is

known, the response of the system to an arbitrary input sequence can be

obtained by summing the responses to all the individual impulses.

The Discrete Sinusoid

•

-4-2 0 2 4

(a)

•

• •

10 12

(d)

•sr-1

-3

£ °

"ST

-3

•

1 0 1

(b)

•

1 0 1

(•)

•

"sr-l

"? 0

• •

1 0 1

(c)

i • •

1 0 1

•

Fig. 2.2 (a) Unit-impulse signal, S(n), —5 < n < 5. (b) An arbitrary discrete signal.

(c),

(d), (e), and (f): The representation of the signal shown in (b) in terms of delayed

and scaled impulses, (c) -S(n + 1), (d) 8(n), (e) -3<J(n - 1), and (f) 2S(n - 2).

Frequency-domain signal representation

An alternate representation of signals is called the frequency-domain rep-

resentation. In this representation, the variation of a signal in terms of fre-

quency is used to characterize the signal. At each frequency, the amplitude

and phase or, equivalently, the amplitudes of the cosine and sine compo-

nents of the sinusoid are required for representing a signal. Figure 2.3(a)

shows two sinusoidal waveforms that are the components of a periodic sig-

nal.

The sum of the projection of the two waveforms on the time axis

is the time-domain representation of the signal, shown in Fig. 2.3(b). Fig-

ure 2.3(c) shows the representation of the signal on the frequency axis. The

amplitude and the phase shift of the first sinusoid are, respectively, 1 and

-60 degrees and those of the second sinusoid are, respectively, 1 and 90 de-

grees.

It is evident that either representation completely specifies the signal.

The independent variable is time in the time-domain representation. In the

frequency-domain, the independent variable is frequency thereby explicitly

specifying the frequency components of a signal. This book is about the

frequency-domain representation of signals. Therefore, we have to explore

the characteristics of the sinusoidal waveform.

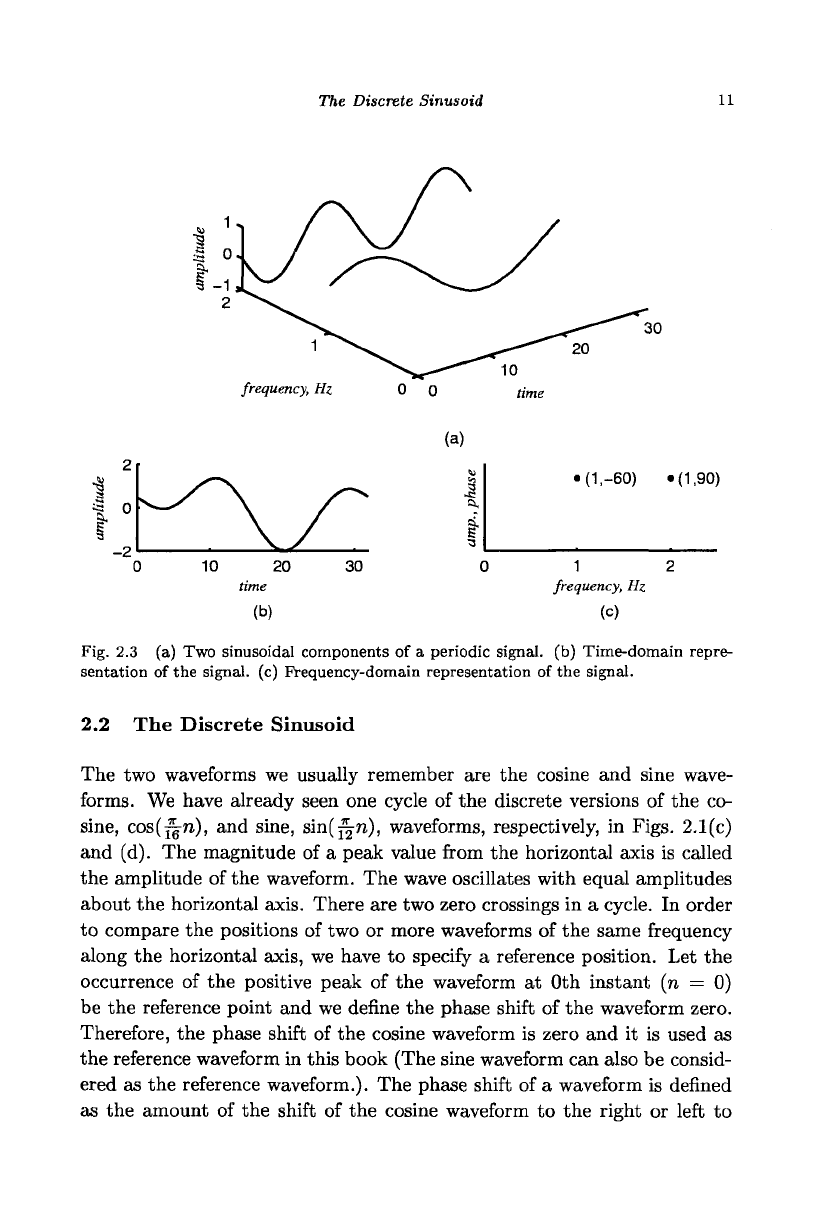
The Discrete Sinusoid

frequency, Hz 0 0 time

• (1,-60) •(1,90)

1 2

frequency, Hz

(c)

Fig. 2.3 (a) Two sinusoidal components of a periodic signal, (b) Time-domain repre-

sentation of the signal, (c) Frequency-domain representation of the signal.

2.2 The Discrete Sinusoid

The two waveforms we usually remember are the cosine and sine wave-

forms.

We have already seen one cycle of the discrete versions of the co-

sine,

cos(j^n), and sine, sin(j^n), waveforms, respectively, in Figs. 2.1(c)

and (d). The magnitude of a peak value from the horizontal axis is called

the amplitude of the waveform. The wave oscillates with equal amplitudes

about the horizontal axis. There are two zero crossings in a cycle. In order

to compare the positions of two or more waveforms of the same frequency

along the horizontal axis, we have to specify a reference position. Let the

occurrence of the positive peak of the waveform at Oth instant (n = 0)

be the reference point and we define the phase shift of the waveform zero.

Therefore, the phase shift of the cosine waveform is zero and it is used as

the reference waveform in this book (The sine waveform can also be consid-

ered as the reference waveform.). The phase shift of a waveform is defined

as the amount of the shift of the cosine waveform to the right or left to

(a)

(b)

The Discrete Sinusoid

obtain that waveform. If the shifting is to the right we define the phase

shift to be negative and a shift to the left is positive. For example, the sine

waveform has a -90 degrees or

—

| radians phase shift since we have to shift

the cosine wave to the right by that amount to get the sine wave. What is

called a sinusoid is a cosine or sine wave with arbitrary phase shift. The

cosine and sine waveforms are important special cases of the sinusoid with

phase shifts of zero and -90 degrees, respectively.

The polar form

A discrete sinusoidal waveform is mathematically characterized as

x(n) = Acos(u>n + 0), n = -co,..

.,—1,0,1,..

.,oo (2.1)

where A is the amplitude (half the peak-to-peak length),

is the angular

frequency of oscillation in radians per sample, and 9 is the phase shift

in radians. The cyclic frequency of oscillation / is ^ cycles per sample.

The period N is 4 samples (The period of a discrete sinusoidal waveform

is j only when \ is an integer. We will consider the more general case

later.).

For the waveform shown in Fig. 2.1(c), the amplitude is 1, the

phase shift is 0 (that is the positive peak of the waveform occurs at the point

n = 0), the angular frequency, u, is f^ radians per sample, and the cyclic

frequency / is ^ cycles per sample. The period is 32 samples, that is, the

waveform repeats any 32-point sequence of its sample values, at intervals of

32 samples, indefinitely, x(n) = x(n ± 32) for any n. The interval between

two samples is ^ = 11.25 degrees. Therefore, the values of the cosine and

sine functions at intervals of 11.25 degrees can be read from this figure. For

the waveform shown in Fig. 2.1(d), the amplitude is 1 and the phase shift

—

^ radians (shift of the cosine waveform by six samples (6/u — —6) to

the right), that is, the positive peak of the waveform occurs after f radians

from the point n = 0. The angular frequency, ui, is y^, and the cyclic

frequency / is ^ cycles per sample. The period is 24 samples, that is, the

waveform repeats any 24-point sequence of its sample values, at intervals

of 24 samples, indefinitely. The values of the sine and cosine functions at

intervals of 15 degrees can be read from this figure. A shift by an integral

number of periods does not change a sinusoid. If a sinusoid is given in terms

of a phase-shifted sine wave, then it can be, equivalently, expressed in terms

of a phase-shifted cosine wave as x (n) = Asm(un+9) = A cos(am+(#-§)).

Conversely, x(n) = Acos(um + 9) = Asm(uin + (9 + f)).

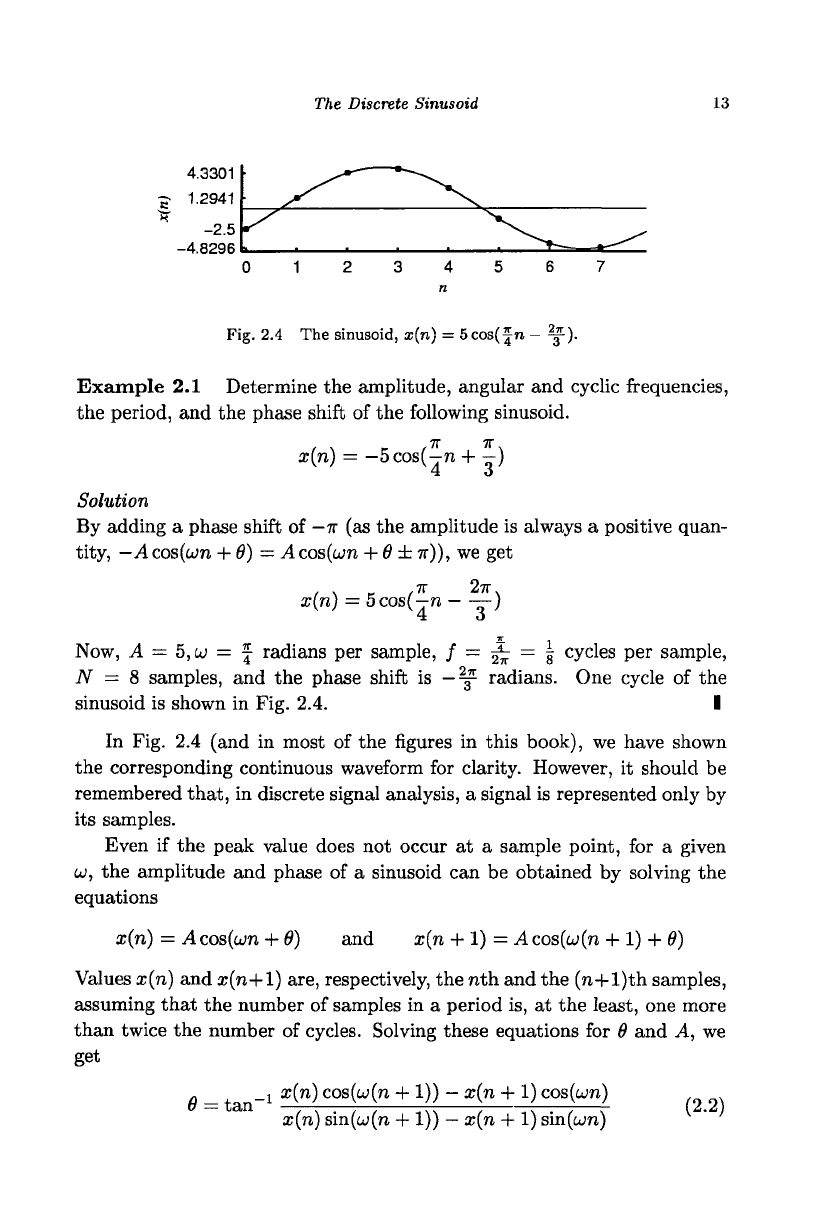
The Discrete Sinusoid

4.3301

-5-

1.2941

"ST

-2.5

-4.8296

Fig. 2.4 The sinusoid, x(n) = 5cos(f n - ^).

Example 2.1 Determine the amplitude, angular and cyclic frequencies,

the period, and the phase shift of the following sinusoid.

x{n) =

—5

cos(—n + —)

Solution

By adding a phase shift of

—7r

(as the amplitude is always a positive quan-

tity, —ACOS(LJTI + 8) = Acos(am + 8 ± 7r)), we get

x(n) = 5cos(— n ——)

T: O

Now, A = 5,w = j radians per sample, / = 2V = g

sample,

N = 8 samples, and the phase shift is

—

^ radians. One cycle of the

sinusoid is shown in Fig. 2.4. I

In Fig. 2.4 (and in most of the figures in this book), we have shown

the corresponding continuous waveform for clarity. However, it should be

remembered that, in discrete signal analysis, a signal is represented only by

its samples.

Even if the peak value does not occur at a sample point, for a given

LJ,

the amplitude and phase of a sinusoid can be obtained by solving the

equations

x(n) = A cos(um + 8) and x(n + 1) = Acos(u(n + 1) + 8)

Values x{n) and x(n+l) are, respectively, the nth and the (n+l)th samples,

assuming that the number of samples in a period is, at the least, one more

than twice the number of cycles. Solving these equations for 6 and A, we

get

x(n) cos(w(n + 1)) - x(n + 1) cos(wn)

—

tan

x(ri) sin(w(n + 1))

—

x(n + 1) sin(wn)

(2.2)