Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

The Discrete Sinusoid

A =

)

cos(am + 0)

' '

Since the tangent function has period

TT,

the signs of the numerator and

denominator must be taken into account in determining the angle 9.

Example 2.2 Let a;(l) = 1 and x(2) = —1 be the two samples of a

sinusoid with frequency / = \ cycles/sample. Find the polar form of the

sinusoid.

Solution

u) = 2nf = f radians/sample. Substituting the values in Eqs. (2.2) and

(2.3),

we get

tan

-l

lcO8

(

)-(-

)

COS

(?)_ * A -

- ,/n

-tan

lsin(7r)-(-l)sin(f) - 4'

~ cos(f - f) "

Therefore, the sinusoid is x(n) = \/2cos(|n

—

f). I

The rectangular form

In the polar form, a sinusoid is represented by its amplitude and phase. In

the rectangular form, a sinusoid is represented in terms of the amplitudes

of its cosine and sine components. By expanding Eq. (2.1), the rectangular

form of representing a sinusoid is obtained as

x(n) = Ccos(am) + -Dsin(wn),

where C = A cos

and D =

—A

sin

The inverse relation is A = VC

+ D

and 9 = cos"

^) = siiT

^).

Example 2.3 Express the following sinusoid in rectangular form.

x(n) = 5cos(— n —)

Solution

C = 5cos(-y) = -2.5, J? = -5sin(-y) = 5^

Therefore, the sinusoid, in the rectangular form, is given by

x(n) = -2.5cos(-n) +5—sin(-n)

The Discrete Sinusoid 15

1.7678

-2 5

D 2 4

(a)

3.0619

- # °

-4.3301

3 2

(b)

Fig. 2.5 (a) The cosine component, x(n) = — 2.5cos( jn), and (b) the sine component,

x(n) = \/3(2.5)sin(^n), of the sinusoid shown in Fig. 2.4.

The sinusoid, and its cosine and sine components are shown, respectively,

in Figs. 2.4, 2.5(a), and (b). We can easily verify that each sample value of

the sinusoid is the sum of the corresponding samples of its cosine and sine

components. I

Example 2.4 Express the following sinusoid in polar form.

in = cos(—n) + sm(—n)

6 6

Solution

A = \/l

+ l

= y/2, 9 =

cos

I —= I = sin

—=.

) =

— —

radians

\V2j \V2j 4

Hence, the sinusoid is given by x(n) = y/2cos(fn

—

j) in the polar form. I

The rectangular form of a sinusoid shows clearly that a sinusoid is a linear

combination of sine and cosine waveforms of the same frequency. This

point is so important that we provide an alternate viewpoint. Any function

x(n) can be expressed as the sum of an even function *W+

*(-")

and

odd function

)-*\-

)

te that, for a periodic function with period

N, x(N

—

n) can also be used instead of

x(—n).

Therefore, an arbitrary

sinusoid, which is neither odd nor even, can be expressed as the sum of

an odd function and an even function. For a sinusoid, the odd function

is a sine function and the even function is a cosine function of the same

frequency.

Acosjun + 6) + Acos(w(N -n) + 6)

vlcos(um + 0) - Acos{u(N - n) +6)

= Acos(6)cos(u:n)

= -Asm(0)sm(un)

The Discrete Sinusoid

Example 2.5 Use even and odd split to find the sample values of the

cosine and sine components of the sinusoid, x(n) = \/2cos(fn

—

J).

Solution

The sample values of the sinusoid for n = 0,1,2,3 are

{1,1,

—1,

—1}.

Using

the even and odd split, we get the sample values of the cosine and sine

components, respectively, as {1,0, -1,0} and

{0,1,0,-1}.

The sum of sinusoids of the same frequency

The sum of discrete sinusoids of the same frequency but arbitrary ampli-

tudes and phases is a sinusoid of the same frequency. Let

#i (n) = A\ cos(um + 9\) and #2(71) = A

cos(om + 9

)

Then,

£3

(n) = x\ (n) + x

(n) = A

cos(un + #3). Expressing the waveforms

in rectangular form, we get

x\(n)

= a\ cos(um) +

sin(um), a\ = A\ cos(#i), 61 = —Ai sin(#i)

£2(71) = a

cos(wn) +

sin(um), 02 = A

cos(9

), b

= —A

sin(#

)

(n)

= a

cos(wn) +

sin(um), a

= A

cos(0

), b

= -A

sin(0

)

It is obvious that a

= ai + 02 and 63 = &i +62- Converting from

rectangular form to the polar form, we get

= y/(

+ a

)

+ (&i + b

)

= yJA\ +A\+

cos(9

- 9

)

_, Ai cos(^i) + A

cos(9

) . _, Ai sin(0i) + A

sin(0

)

— cos -——. -— = sin -—'—

By repeatedly adding, any number of sinusoids of the same frequency can

be combined into a single sinusoid.

Example 2.6 Determine the sinusoid that is the sum of the two sinusoids

(n) = -4.3cos(|n- f$) and x

(n) =3.2cos(fn- f).

Solution

The first sinusoid can also be expressed as xi (n) = 4.3 cos(|n + ^jf

)•

Now,

4.3,

=3.2, <?i = ^,

2 = -|

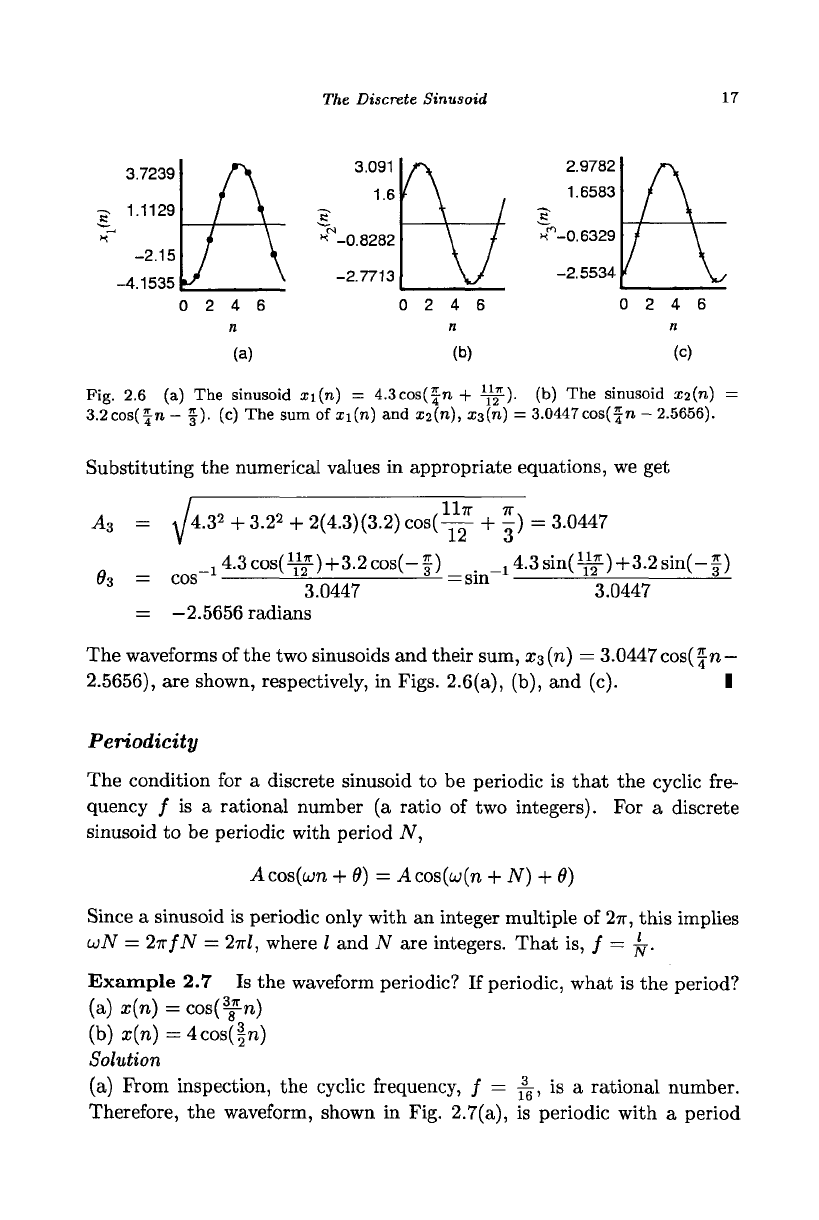
The Discrete Sinusoid

3.7239

1.1129

-2.15

-4.1535

0 2 4 6

2.9782

1.6583

^T-0.6329

-2.5534

(b)

0 2 4 6

(c)

Fig. 2.6 (a) The sinusoid xi(n) = 4.3cos(|n + ^f

). (b) The sinusoid X2(n)

3.2cos(fn- |). (c) The sum of n(n) and

(n),

(n) = 3.0447 cos(fn - 2.5656).

Substituting the numerical values in appropriate equations, we get

= W4.3

+3.22+ 2(4.3)(3.2)cos(^ + |)= 3.0447

4.3cos(^)+3.2cos(-f) _, 4.3sin(^f)+3.2sin(-f)

= cos Hr^rTT^ — =sin — —

3.0447

= —2.5656 radians

3.0447

The waveforms of the two sinusoids and their sum, X3(n) = 3.0447 cos(fn-

2.5656), are shown, respectively, in Figs. 2.6(a), (b), and (c). I

Periodicity

The condition for a discrete sinusoid to be periodic is that the cyclic fre-

quency / is a rational number (a ratio of two integers). For a discrete

sinusoid to be periodic with period N,

Acos(un + 6) = Acos(uj(n + N) + 9)

Since a sinusoid is periodic only with an integer multiple of 27r, this implies

LJN

= 2nfN = 2irl, where / and N are integers. That is, / = jj.

Example 2.7 Is the waveform periodic? If periodic, what is the period?

(a) x(n) = cos(^

(b) x(n) = 4cos(|n)

Solution

(a) From inspection, the cyclic frequency, / = ^, is a rational number.

Therefore, the waveform, shown in Fig. 2.7(a), is periodic with a period

The Discrete Sinusoid

(a)

•S-

(b)

Fig. 2.7 (a) The sinusoid x(n) = cos( ^-n) is periodic with a period of

= 16 samples.

(b) The sinusoid x(n) = 4cos(|n) is not periodic.

of 16 samples. The waveform repeats any 16-point sequence of its sample

values, at intervals of 16 samples, indefinitely.

(b) Prom inspection, the cyclic frequency, / =

j^,

is an irrational number.

Therefore, the waveform, shown in Fig. 2.7(b), is not periodic. I

Highest frequency for unique representation

A sinusoid which completes k cycles in its period has a distinct set of 2k +1

sample values. Due to the representation of a waveform by a finite number

of samples, in practice, sinusoids with a finite number of frequencies only

can be uniquely identified. Consider the following identities with positive

integers N, m, and k.

,2TT.

,2TJ\

cos(—(k + mN)n + 0) = cos(—fcn + 0)

•N

.2TT

2TT

cos(—(mN

—

k)n + 6) = cos(—kn

—

-N

(2.4)

(2.5)

With increasing frequencies, oscillations increase only up to k — y (with

N even), decrease afterwards, and cease at k = N. This pattern continues

forever. Therefore, sinusoids with k up to ^ ~ 1

^y (f°

cosine waves k

up to Y)

can De

uniquely identified with N samples.

Example 2.8 Specify two higher frequency sinusoids with the same set

of sample values as that of

x[n) =4sm(-n + -)

Solution

Two of the innumerable number of sinusoids with the same set of sample

The Discrete Sinusoid 19

0 12 3

Fig. 2.8 The sinusoids x(n) = 4sin(|ra + *•), x(n) = 4sin(5|ra + |), and x(n) ~

—4sin(3^n

—

^). All the three sinusoids have the same set of sample values.

values are

/ \ J . /57T 71". . . .37T 7T.

x(n) = 4sm(—n + -), x(n) = -4sin(yn - -)

The three waveforms are shown in Fig. 2.8. I

Harmonically related sinusoids

Harmonically related sinusoids are a set of sinusoids, called harmonics, com-

prising a fundamental harmonic with a frequency / and other harmonics

having frequencies nf, where n is a positive integer. The frequency of

the second harmonic is 2/, that of the third harmonic is 3/, and so on.

The nth harmonic completes n cycles during the period of the fundamen-

tal.

For example, the fundamental 3cos(||-n + f), the second harmonic

-2cos(ff2n + f), and the third harmonic cos(|f3n + f) are shown in

Fig. 2.9. The sum of discrete sinusoids with harmonically related frequen-

cies is not sinusoidal, but it is periodic.

Example 2.9 Find the period of the combination of the sinusoids. Plot

one period of the waveform of the first, the sum of the first and second, and

the sum of the three of the frequency components.

. , 8 . . .2TT , 1 . .2TT . 1 . ,27r

„

x(n) = ^(sm(-n) - - sin(-3n) + - sin(-5n))

Solution

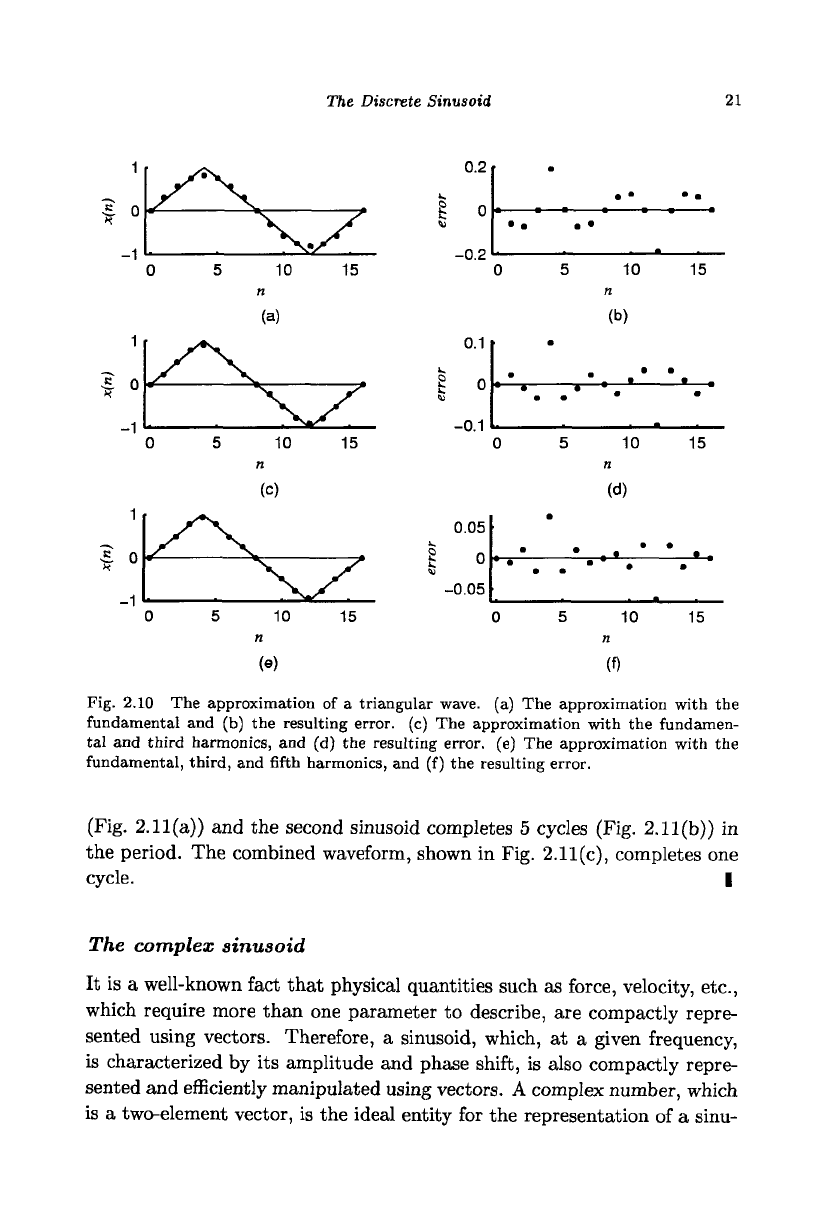
This is an approximation of the triangular waveform with amplitude one.

The period is 16. Only the fundamental harmonic is shown in Fig. 2.10(a)

with dotted line. The error in this representation is shown in Fig. 2.10(b).

Figures 2.10(c) and (d) show, respectively, an approximation and the error

with the sum of the first and third harmonics. Figures 2.10(e) and (f) show,

The Discrete Sinusoid

0 5 10 15

Fig. 2.9 The fundamental x(n) = 3cos(y|-7i + |-), the second harmonic x(n) =

-2cos(|^2ra + j), and the third harmonic x(n) = cos(^3n + j). All the three si-

nusoids are periodic with a period of N = 16 samples.

respectively, the sum of the first, third, and fifth harmonics, and the result-

ing error in the approximation. Note that the error in the approximation

of the triangular waveform reduces as more and more harmonics are used.

To find the period of the combination of sinusoids of various rational

cyclic frequencies: (i) cancel out any common factors of the numerators

and denominators of each of the frequencies and (ii) divide the greatest

common divisor of the numerators by the least common multiple of the

denominators of the frequencies. This yields the fundamental frequency.

The denominator of the fundamental frequency is the fundamental period.

Example 2.10 Find the fundamental cyclic frequency of the sum and

the harmonic numbers of the two sinusoids.

xi(n) = cos(yn-—), x

{n) = sin(yn - -)

Solution

The cyclic frequency of the waveforms are /i = | and fi = \- There are no

common factors of the numerators and denominators. The least common

multiple of the denominators (5,3) is 15. The greatest common divisor of

the numerators (2,1) is one. Therefore, the fundamental cyclic frequency

is TE-.

Tne

fundamental period is 15 samples. Frequency /i is the 6th

harmonic and /•! is the 5th harmonic. The first sinusoid completes 6 cycles

The Discrete Sinusoid

t °

0.2

-0.2

10 15

(b)

(e)

0.1

-0.1

0.05

-0.05

10 15

(d)

5 10 15

(f)

Fig. 2.10 The approximation of a triangular wave, (a) The approximation with the

fundamental and (b) the resulting error, (c) The approximation with the fundamen-

tal and third harmonics, and (d) the resulting error, (e) The approximation with the

fundamental, third, and fifth harmonics, and (f) the resulting error.

(Fig. 2.11(a)) and the second sinusoid completes 5 cycles (Fig. 2.11(b)) in

the period. The combined waveform, shown in Fig. 2.11(c), completes one

cycle. |

The complex sinusoid

It is a well-known fact that physical quantities such as force, velocity, etc.,

which require more than one parameter to describe, are compactly repre-

sented using vectors. Therefore, a sinusoid, which, at a given frequency,

is characterized by its amplitude and phase shift, is also compactly repre-

sented and efficiently manipulated using vectors. A complex number, which

is a two-element vector, is the ideal entity for the representation of a sinu-

The Discrete Sinusoid

*M *M *i*

0 5 10 15 0 5 10 15 0 5 10 15

n n n

(a) (b) (c)

Fig. 2.11 (a) The sinusoid xi(n) = cos(^n

—

f^) completes 6 cycles during 15 samples.

(b) The sinusoid X2{n) = sin(^n - |) completes 5 cycles during 15 samples, (c) The

sum of the two sinusoids completes one cycle during 15 samples. All the three waveforms

are periodic with a period of N = 15 samples.

soid. With this representation, we get the advantage of manipulating both

the amplitude and phase of a sinusoid at the same time.

Although physical systems always interact with real signals, it is often

mathematically convenient to represent real signals in terms of complex

signals. We are looking for a single entity that represents both cosine

and sine functions in a compact form and is much easier to manipulate.

This function is the complex exponential or complex sinusoid representing

a rotating vector as described in Appendix A. The complex exponential

function is a functionally equivalent mathematical representation of the

sinusoidal waveform, but is more convenient for manipulation than the

cosine and sine functions.

The complex exponential function with an imaginary argument is given

x(n) = Ae>t

un+

V = Ae

iwn

, n = -oo,...,

-1,0,1,...

,oo

The term e

" is the complex sinusoid with unit amplitude and zero

phase shift. This form of the sinusoid is more commonly used in theoret-

ical and practical Fourier analysis due to its compact form and ease and

efficiency of manipulation. By multiplying with the complex (amplitude)

coefficient Ae^, we can generate a complex sinusoid with arbitrary am-

plitude and phase shift. The complex coefficient Ae

is a single complex

number containing both the amplitude and phase of a sinusoid.

The complex conjugate of the complex exponential is Ae~

un+0

\ By

adding the complex exponential with its conjugate and dividing by two,

The Discrete Sinusoid

due to Euler's identity, we get

(

) = ^(

i(^n+fi)

+ e

-j(«n+«)j

cos

(

n + 9)

The right side of this equation is a real sinusoid described earlier, which is

of interest in practical applications. Note that the terms appearing on the

left-hand side are complex conjugates which combine to represent the real

function A cos (am + 6). The plot of the amplitude and phase (or the real

and imaginary parts) of the complex coefficients of the complex sinusoids

of a signal against frequency is its complex spectrum.

Example 2.11 Find the spectrum of the signal.

/ \ /I* 27T.

x(n) = 8cos(-n- —)

Solution

The waveform is shown in Fig. 2.12(a). Since u = 2nf = |, / = i

cycles/sample. Expressing the waveform in terms of complex sinusoids, we

get

(n) = ^(e^t«-¥)

-i(f«-¥))

The complex frequency coefficients are

4e~

and

4e-

Therefore, the

amplitude and phase of the spectrum at / = ^ are 4 and

—

^p radians

and those at / =

—

^ are 4 and ^-, respectively. The spectrum, in terms

of amplitude and phase, is shown in Fig. 2.12(b). The real and imaginary

parts of the spectrum and the corresponding cosine and sine components

of the sinusoid are shown, respectively, in Figs. 2.12(c) and (d).

It should be observed that the real part (as well as the amplitude) of the

spectrum is even-symmetric and the imaginary part (as well as the phase)

is odd-symmetric. We use four real values to represent a real sinusoid

instead of two. This redundancy, in terms of storage and operations, can

be eliminated as described in a later chapter. I

Both the dc and the frequency component with frequency index y (with

N even) have only real spectral values, A or —A, for real signals. That

means the phase shift of these frequency components is 0 or ±n. It should

be noted that real sinusoids are easy to visualize, while complex sinusoids

are easy to manipulate.