Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

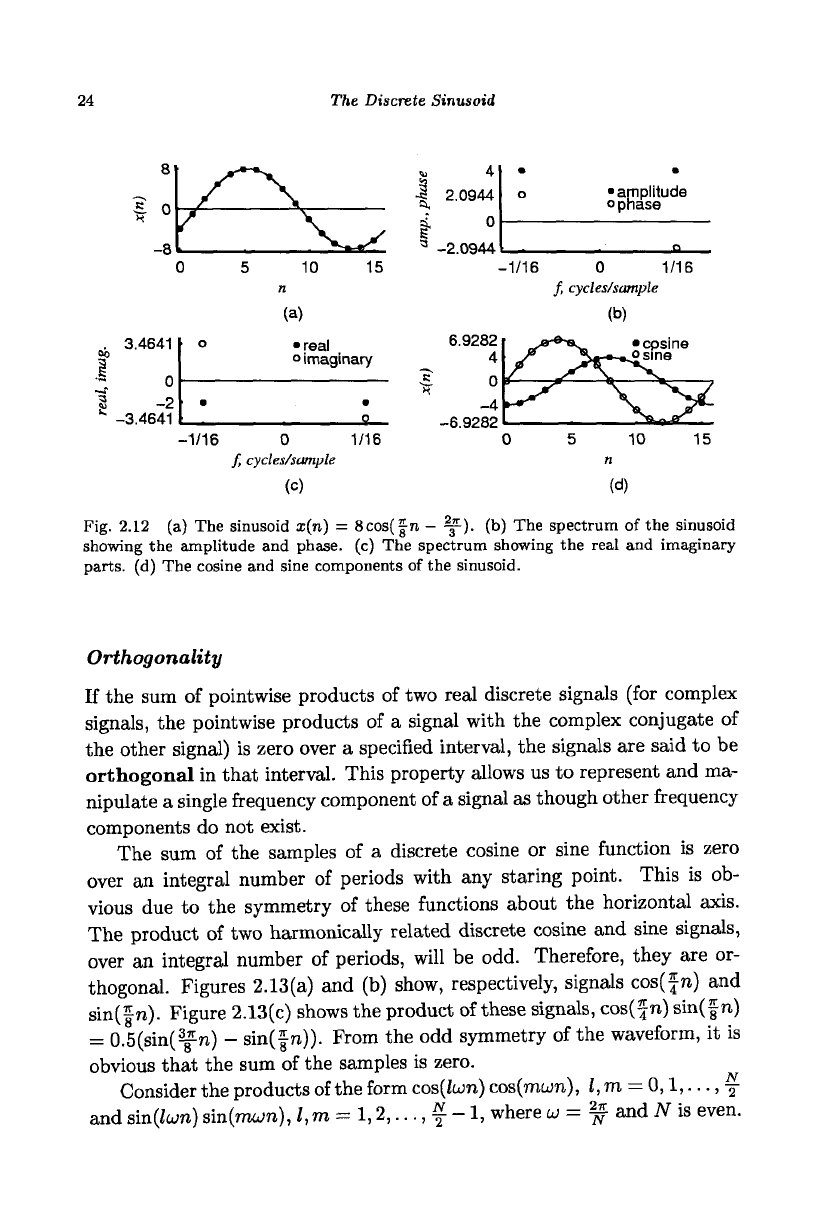
24 The Discrete Sinusoid

-8

(a)

. 3.4641

a 0

-2

^ -3.4641

•

• real

o imaginary

•

.,9

-1/16 0 1/16

/ cycles/sample

(c)

2.0944

-2.0944

•amplitude

ophase

-1/16 0 1/16

/ cycles/sample

(b)

• cpsine

osine

(d)

Fig. 2.12 (a) The sinusoid x(n) = 8cos(|n - ^p). (b) The spectrum of the sinusoid

showing the amplitude and phase, (c) The spectrum showing the real and imaginary

parts,

(d) The cosine and sine components of the sinusoid.

Orthogonality

If the sum of pointwise products of two real discrete signals (for complex

signals, the pointwise products of a signal with the complex conjugate of

the other signal) is zero over a specified interval, the signals are said to be

orthogonal in that interval. This property allows us to represent and ma-

nipulate a single frequency component of a signal as though other frequency

components do not exist.

The sum of the samples of a discrete cosine or sine function is zero

over an integral number of periods with any staring point. This is ob-

vious due to the symmetry of these functions about the horizontal axis.

The product of two harmonically related discrete cosine and sine signals,

over an integral number of periods, will be odd. Therefore, they are or-

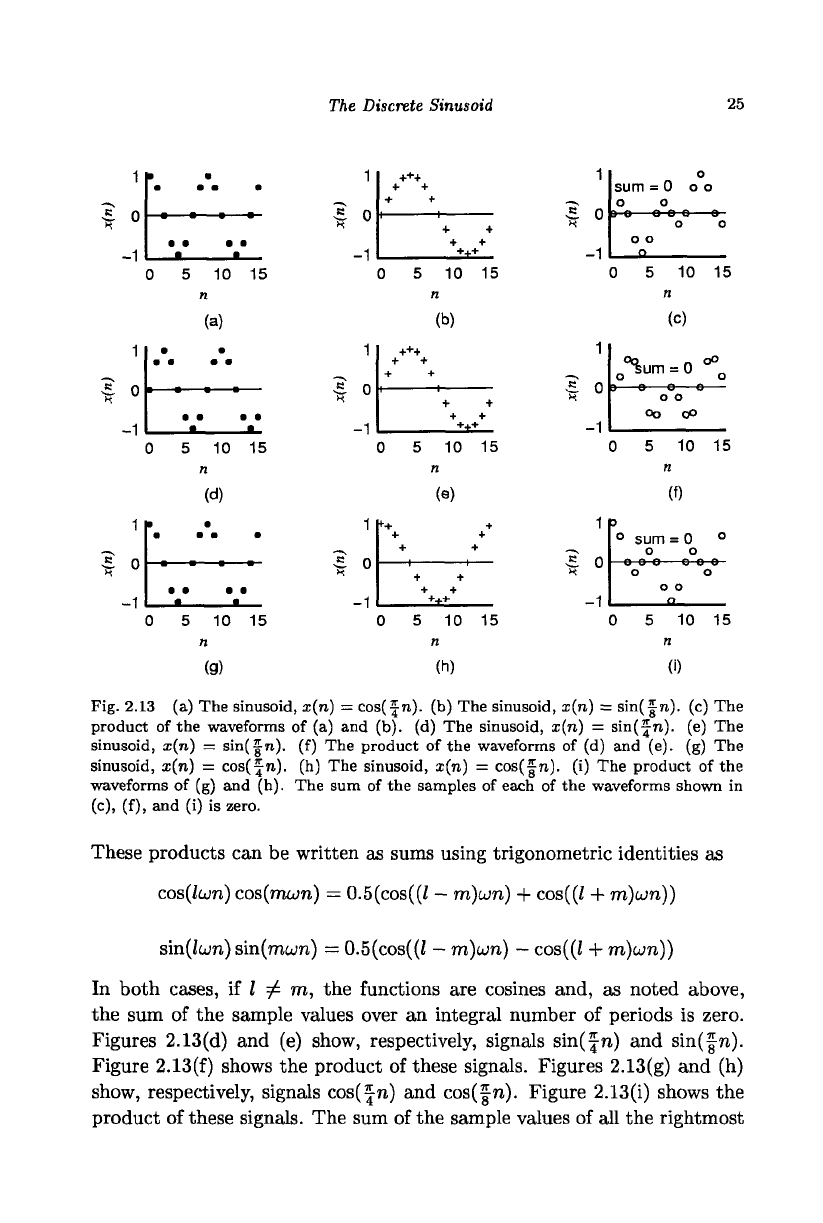
thogonal. Figures 2.13(a) and (b) show, respectively, signals cos(f n) and

sin(f

n).

Figure 2.13(c) shows the product of these signals, cos(f n) sin(fn)

= 0.5(sin(^n) - sin(f

n)).

From the odd symmetry of the waveform, it is

obvious that the sum of the samples is zero.

Consider the products of the form cos(Zam) cos(mwn), I, m = 0,1,

and sin(Jwn) sin(mum), /, m =

1,2,...,

where

= ^ and N is even.

The Discrete Sinusoid

* °

f °

• «

• B • B

SB B S

0 5 10 15

(a)

B B

SB SB

0 5 10 15

(d)

B B B B

B • B B

0 5 10 15

(g)

+ +

+4-+

0 5 10 15

(b)

t °

+++

+ +

+4.+

0 5 10 15

(e)

+ +

+4-+

0 5 10 15

(h)

sum = 0 o o

o o

0 5 10 15

(c)

5 0

o o

oo o°

0 5 10 15

(f)

° sum

= 0

o o

0 5 10 15

(i)

Fig. 2.13 (a) The sinusoid, x(n) = cos(^n). (b) The sinusoid, x(n) = sin(^n). (c) The

product of the waveforms of (a) and (b). (d) The sinusoid, x(n) = sin( Jn). (e) The

sinusoid, x(n) = sin(Ju). (f) The product of the waveforms of (d) and (e). (g) The

sinusoid, x(n) = cos(^n). (h) The sinusoid, x(n) = cos(^n). (i) The product of the

waveforms of (g) and (h). The sum of the samples of each of the waveforms shown in

(c),

(f), and (i) is zero.

These products can be written as sums using trigonometric identities as

cos(Zom) cos(mam) = 0.5(cos((Z

—

m)um) + cos((Z + m)um))

sin(Zo;n) sin(mwn) = 0.5(cos((Z - m)um)

—

cos((Z + m)um))

In both cases, if I =£ m, the functions are cosines and, as noted above,

the sum of the sample values over an integral number of periods is zero.

Figures 2.13(d) and (e) show, respectively, signals sin(Jn) and sin(|n).

Figure 2.13(f) shows the product of these signals. Figures 2.13(g) and (h)

show, respectively, signals cos(|n) and cos(|n). Figure 2.13(i) shows the

product of these signals. The sum of the sample values of all the rightmost

The Discrete Sinusoid

0.1464

(a)

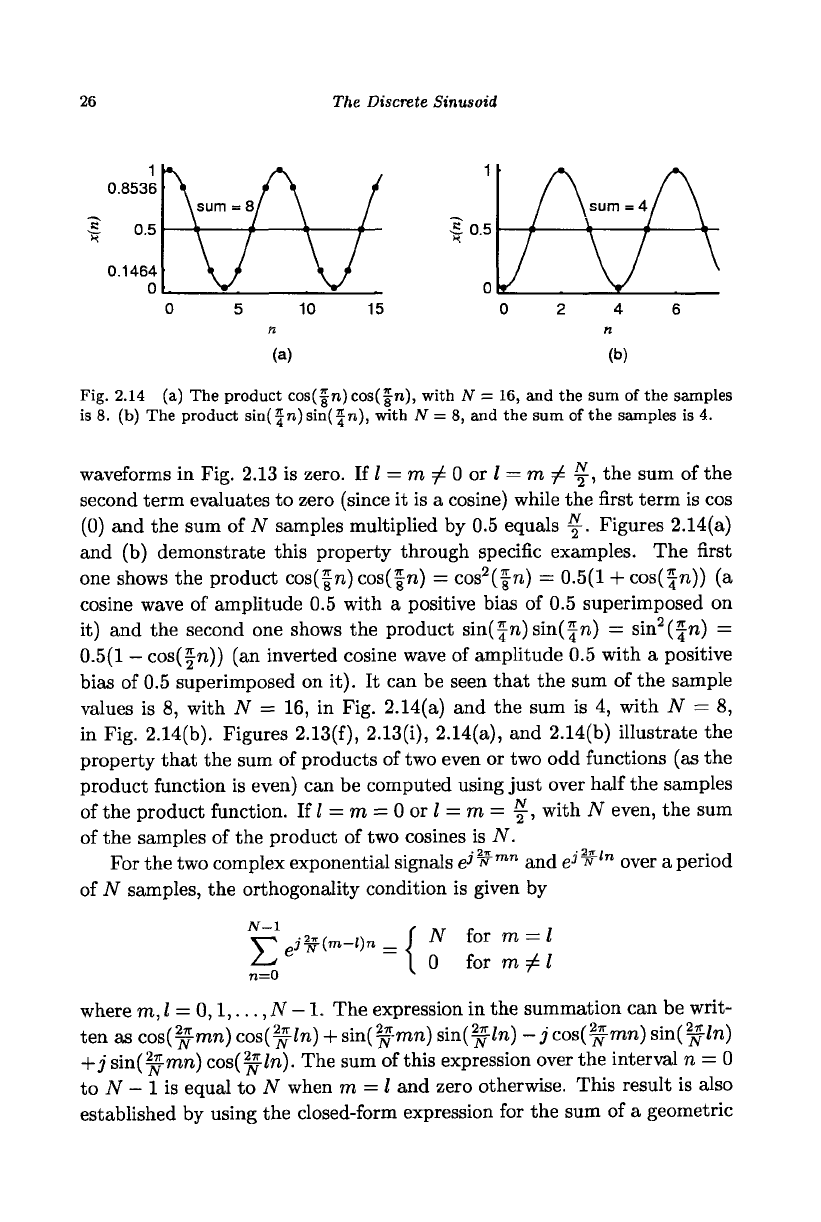
Fig. 2.14 (a) The product cos(£ n)cos( Jn), with N = 16, and the sum of the samples

is 8. (b) The product sin(f

n)sm(^n),

with N = 8, and the sum of the samples is 4.

waveforms in Fig. 2.13 is zero. If I = m ^ 0 or I = m ^ ^> *^

e sum

°f *^

second term evaluates to zero (since it is a cosine) while the first term is cos

(0) and the sum of N samples multiplied by 0.5 equals y. Figures 2.14(a)

and (b) demonstrate this property through specific examples. The first

one shows the product cos(fn) cos(|n) = cos

(f-n) = 0.5(1 + cos( |n)) (a

cosine wave of amplitude 0.5 with a positive bias of 0.5 superimposed on

it) and the second one shows the product sin(|n)sin(|n) = sin

(|n) =

0.5(1

—

cos(|n)) (an inverted cosine wave of amplitude 0.5 with a positive

bias of 0.5 superimposed on it). It can be seen that the sum of the sample

values is 8, with N = 16, in Fig. 2.14(a) and the sum is 4, with JV = 8,

in Fig. 2.14(b). Figures 2.13(f), 2.13(i), 2.14(a), and 2.14(b) illustrate the

property that the sum of products of two even or two odd functions (as the

product function is even) can be computed using just over half the samples

of the product function. If/ = m = 0or/ = m= y, with N even, the sum

of the samples of the product of two cosines is N.

For the two complex exponential signals e

and e

over a period

of N samples, the orthogonality condition is given by

JV-l

n=0

'-(m-l)

N for m =

for m/I

where m, / =

0,1,...,

N -1. The expression in the summation can be writ-

ten as cos(^mn) cos(%ln) + sin(%-mn) sin(^-in) -jcos(^mn) sin(%ln)

+j sin(^-mn) cos(^Zn). The sum of this expression over the interval n = 0

to N - 1 is equal to N when m = I and zero otherwise. This result is also

established by using the closed-form expression for the sum of a geometric

5ummorj/

d Discussion

progression, when m / / (when m

—

l, the summation is equal to N).

£ ei^(m-0n

2ir(

= 0, for m * l

n=0

J—w—

2.3 Summary and Discussion

• In addition to appreciating the necessity of representing arbitrary

signals as a linear combination of simple signals, in this chapter, we

learned the properties of a discrete sinusoid and the efficient way

to represent it mathematically.

• Most signals that occur in practical applications are continuous-

time signals having arbitrary amplitude profile. These signals are

very difficult to manipulate analytically and numerical methods are

resorted to using the discrete signal obtained by sampling the signal

at periodic intervals.

• While numerical processing enables us to manipulate arbitrary sig-

nals,

it requires considerable computational effort. When the dis-

crete signals are represented in terms of their frequency compo-

nents,

it turns out that the computational effort required for signal

processing operations is reduced significantly.

• In the frequency-domain representation of signals, a signal is rep-

resented as a linear combination of a set of sinusoids. A sinusoid

itself is a linear combination of sine and cosine waveforms of the

same frequency. The sine and cosine waveforms are defined as the

vertical and horizontal projection, respectively, of a point moving

around a circle, with center at origin, at uniform angular velocity.

Therefore, the most efficient way of representing a sinusoid is using

the function

iuin

which represents a point moving around the unit

circle at angular velocity u.

• The representation of signals in terms of sinusoids is very efficient

because of the advantageous properties of the sinusoids. The or-

thogonality property implies that the representation and manipu-

lation of a sinusoid at a specific frequency can be carried out with

the assumption that no other sinusoids are present in a signal.

• A time-domain signal can be decomposed into a set of scaled and

delayed impulses or sinusoids with various frequencies, amplitudes,

The Discrete Sinusoid

and phases. The representation using sinusoids is more efficient for

the analysis and design of signals and systems. However, signals do

not occur in this form naturally. Therefore, we have to derive the

frequency-domain representation of a signal from its time-domain

representation. The Fourier transform is the tool to do this job.

In the next chapter, we shall find out the relationship between the

time-domain and the frequency-domain representation of signals.

Reference

(1) Cadzow, J. A. and Van Landingham, H. F. (1985) Signals, Systems,

and Transforms, Prentice-Hall, New Jersey.

Exercises

2.1 Determine the amplitude, angular and cyclic frequencies, the period,

and phase of the sinusoid.

2.1.1.

x(n) = 7sin(fn+f)

* 2.1.2 x(n) = -7.1sin(fn- 2=)

2.1.3 i(r») = -2.2cos^fn)

2.1.4 i(n) = 3cos(|n+ f)

2.1.5 x(n) = -1.1 sin(ffn)

2.2 Given two adjacent samples and the frequency of a sinusoid, find the

polar form of the sinusoid.

2.2.1.

x(0) = 2>/2,a:(l) = (-%/2)(V3 - l),w = f

2.2.2 x(0) = ^,x(l) = =^,u=

* 2.2.3 ar(l) = (^)(V5 - l),z(2) = (=^)(V3 - l),a, = f

2.2.4 x(2) = (=^),x(3) = (=^)(V3 + l),u = f

2.2.5 a:(0) = >/3,a:(l) -

(^)(\/3

- l),w = |

2.3 Express the sinusoid in rectangular form.

2.3.1 x(n) = 5cos(|n+f)

2.3.2 x(n) = cos(f n - \)

2.3.3z(n) = 4sin(fn + f)

2.3.4 x{n) = 2cos(f|n)

2.3.5 x(n) = 7cos(ffn-f).

Exercises

* 2.3.6z(n) = 3cos(fn + f)

2.3.7 x(n) = sin(^n)

2.4 Express the sinusoid in polar form.

2.4.1 x(n) = -4cos(fn) +4sin(fn)

2.4.2 x(n) = cos(^n) + v^Jsin(^n)

2.4.3 x(n) = \/3cos(ff n) + sin(ff n)

2.4.4 x(n) = cos(f n) - V^in^n)

* 2.4.5 x(n) = -cos(fn) -sin(fn)

2.4.6 i(n) = -3sin(fn).

2.4.7 x(n) = -2cos(fn).

2.5 Determine the sinusoid that is the sum of the pair of sinusoids.

2.5.1 2.3cos(fn+f),-7.1sin(|n-^)

2.5.2 2.7cos(fn),-sin(fn)

* 2.5.3 4.7cos(fn-j|),cos(fn- f)

2.5.4 2.2cos(fn),l.lcos(fn)

2.5.5 1.2sin(|n),3.1sin(fn)

2.6 Is the waveform periodic? If periodic, what is the period?

2.6.1 x(n) = cos(0.37rn)

2.6.2 x(n) = cos(\/37m)

2.6.3 x(n) = cos(^|n)

* 2.6.4 x(n) = sin(i^n)

2.6.5 x(n) = 3 + cos(7rn) + cos(2n)

2.7 Find the polar form of three higher frequency sinusoids with the same

set of sample values as that of x(n).

2.7.1 x(n) = 5cos(fn+ f)

* 2.7.2 s(n) = sin(^n-f)

2.8 Find the fundamental cyclic frequency of the sum and the harmonic

numbers of the two sinusoids.

* 2.8.1 cos(^n),cos(^n)

2.8.2 cos(^n),cos(fn)

2.8.3 5,sinfn

2.9 Find the spectrum of the signal in terms of: (i) amplitude and phase

and (ii) real and imaginary parts.

2.9.1 x(n) =6cos(fn+ f)

The Discrete Sinusoid

* 2.9.2 a;(n) = 4cos(fn-f)

2.9.3 x(n) = cos(^n) + \/3sin(^n)

2.9.4 x(n) = lOsin(fn)

2.9.5 x(n) = -2cos(fn)

2.9.6 x\n) = -2

2.9.7 x(n) = 3cos(7rn)

Programming Exercises

2.1 Write a program to generate the sample values of a real discrete sinu-

soid, Acos(jj-n + 6), with period N, phase 6, and amplitude A.

2.2 Write a program to generate the sample values of a complex discrete

sinusoid, Ae^^

n+8

\ with period N, phase 6, and amplitude A.

Chapter 3

The Discrete Fourier Transform

In this chapter, the tools that enable the conversion between the time-

and frequency-domain representations of discrete signals, the DFT and the

IDFT, are derived. These are the mathematical formulations of the problem

of waveform analysis and synthesis, respectively, with harmonically related

discrete sinusoids as the basis functions. An infinite number of sinusoids

with various frequencies, in general, are required for the accurate analysis

and synthesis of an arbitrary waveform. But, out of necessity, only a finite

number of sinusoids are used in practice. The consequences of this limi-

tation will be considered in Chapter 11. For the time being, we assume

that, unless otherwise stated, the constituent frequency components of a

real periodic signal, with N (N even) samples in a cycle, are sinusoids with

frequency indices

0,1,...,

y only. Note that the sinusoid with zero fre-

quency index is a dc signal and the sinusoid that can be represented with

the frequency index y is a cosine waveform. The DFT is defined for any

length. But, due to the availability of fast algorithms with high regularity,

the lengths those are integral powers of two are most often used in prac-

tice.

Therefore, we put emphasis on these lengths in the development of

the DFT theory and algorithms.

In Sec. 3.1, the DFT and the IDFT expressions are obtained through

a simple example. In Sec. 3.2, the DFT and the IDFT expressions are

formally derived and the symmetry property of the DFT kernel matrix is

analyzed. In Sec. 3.3, the closed-form expressions of the DFT of some

simple signals are derived. In Sec. 3.4, the direct computation of the DFT

is described. In Sec. 3.5, the advantages of sinusoidal representation of

signals are listed.

The Discrete Fourier Transform

3.1 The Fourier Analysis and Synthesis of Waveforms

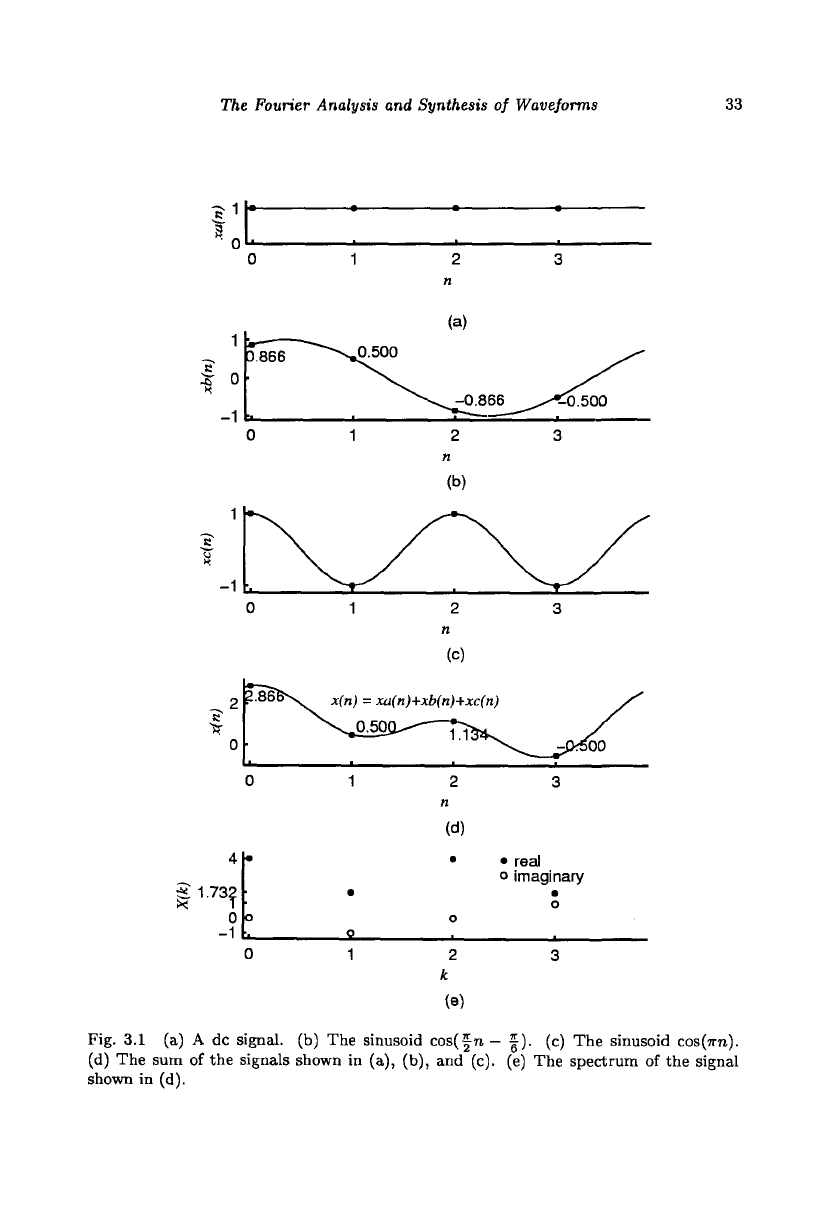
Consider the waveform shown in Fig. 3.1(d) with sample values 2+^, |,

2—

^, and

—

|. The waveform is periodic with a period of 4 samples and one

cycle of which is shown. The problem of Fourier analysis is to find the

sinusoids, the superposition summation of which yields this waveform. The

solution is shown in Fig. 3.1: (a) a dc component xa(n) = 1, (the spectral

value X(0) = 1), (b) a sinusoid xb(n) = cos(f n - f), (X(l) = ^ - j\

and X(3) = ^ +

j\),

and (c) a sinusoid xc(n) = cos(7rn), (X(2) = 1).

The sums of the corresponding sample values of these three waveforms are

equal to the sample values of the waveform shown in Fig. 3.1(d), x(n) —

xa(n) + xb(n) + xc(n).

The spectrum of x(n) is displayed in Fig. 3.1(e) with a scale factor of 4.

The real part of the spectrum X(k) is marked with the symbol '•' and the

imaginary part is indicated by the symbol V. The two problems in Fourier

analysis are: (i) given the time-domain waveform of a signal, how do we get

the coefficients of the individual sinusoids (analysis) and (ii) given the coeffi-

cients of the individual sinusoids, how do we get the combined time-domain

waveform (synthesis). We have started with the problem and the solution

in order to easily understand the problem formulation and the method of

obtaining the solution. The periodic sequence shown in Fig. 3.1(d) can be

considered as the output of a single complex signal generator or, equiva-

lent^, the output of three simple signal generators connected in series as

shown, respectively, in Figs. 3.2(a) and (b).

The Fourier analysis of waveforms

Each frequency component contributes to the value of the time-domain

waveform at each sample point. By multiplying each of the complex fre-

quency coefficient by the sample value of the corresponding complex sinu-

soid and summing the products must be equal to the time-domain sample

value. Therefore, we set up four simultaneous equations with four time-

domain samples.

X(0)e^(«)(o)

x(l)e^(OW + X(2)eJT(°)(

) +X(3)e^(o)(3)

= x

(

)

l(0)e^«(o) +X(l)e^(i)W +I(2)e*TP)P) +X(3)e^W(3) =

(l)

X(0)e^(

)W +X(l)e^(

)(

) +X(2)e^(

)W +X(3)e^(2)(3)

= X

(

)

X(0)e^(3)(o) + X(i)e»*(3)(D + X(2)<W><

> +X(3)e^(3)(3)

= x(3

)

The Fourier Analysis and Synthesis of Waveforms

(b)

(c)

(d)

«. 1.73?

X 1

-1

•

•.

•

• real

o imaginary

•

(e)

Fig. 3.1 (a) A dc signal, (b) The sinusoid cos(f n - |). (c) The sinusoid

COS(TTO).

(d) The sum of the signals shown in (a), (b), and (c). (e) The spectrum of the signal

shown in (d).