Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

The Discrete Fourier Transform

f-1

x(n)

= ± J2 ^WW^

,n = -(j),-(^-l),...,~ -1(3.9)

The values of these forms of DFT and IDFT results in a better display with

the value with index zero in the middle and these forms are also convenient

to derive certain derivations. The spectrum of the waveform shown in

Fig. 3.1(d) in the usual format is X(0) = 4, X(l) = V3 - jl, X{2) = 4,

X(3) — y/3+jl. The same spectrum in center-zero format is X(—2)

—

X(-l) = y/3 + jl, X(0) = 4, X{1) = V3 - jl. Getting one format of

the spectrum or the signal from the other involves a circular shift by ^

positions (swapping of the positive and negative halves).

3.3 DFT Representation of Some Signals

In this section, we derive the DFT of some simple signals analytically.

Although the primary use of the DFT, in practice, is to analyze arbitrary

waveforms through a numerical procedure, finding the DFT of some simple

signals analytically improves our understanding and the resulting closed-

form solutions serve as test cases for the algorithms.

The impulse, x(n) — 6(n)

X{k) = ^ 1 = 1 and S(n) & 1

n=0

(The double-headed arrow indicates that the two quantities are a DFT

pair, that is the frequency-domain function is the DFT of the time-domain

function.) Since the impulse signal is zero except at n = 0, for all k, the

DFT coefficient is unity. All the frequency components exist with equal

amplitude and zero phase.

Example 3.1 Figures 3.6(a) and (b) show, respectively, the unit-impulse

signal and its spectrum, with N = 16. The representation of the impulse

signal, in terms of complex exponentials, is given by

k=0

DFT Representation of Some Signals 45

_ 1

•

'Sf

(a)

_ 1

* 0

, f

f f

5 10

(b)

5 10

Fig. 3.6 (a) The unit-impulse signal, with N = 16, and (b) its spectrum, (c) A dc

signal, with N = 16, and (d) its spectrum.

To find the real sinusoids that constitute the impulse signal, we add the

corresponding positive and negative frequency components. For example,

the sinusoid with frequency index one is obtained as

The representation of the impulse signal, in terms of real sinusoids, is given

2?r

S(n) = —(1 + 2 5T(cos(— nk)) + cosfrn)), n =

0,1,...,

A dc component with amplitude ^, a cosine waveform with amplitude ^

and frequency index 8, and cosine waveforms with amplitude | and fre-

quency indices from 1 to 7 make up the impulse. We can find out the

real sinusoids using the first half of the frequency coefficients due to the

conjugate symmetry of the spectrum of real-valued data. For example, at

frequency index one, the value of the complex coefficient is 1, with mag-

nitude 1 and phase zero. A sinusoid with these characteristics is a cosine

wave with amplitude | (taking into account the scale factor).

Due to the duality (explained in the next chapter) of the time- and

frequency-domains, the DFT of the dc signal, shown in Fig. 3.6(c), is an

impulse, shown in Fig. 3.6(d). The impulse at frequency index zero cor-

responds to a complex exponential with its exponent zero, yielding a dc

signal in the time-domain. I

The Discrete Fourier Transform

The complex exponential

The complex exponential signal, as we have already mentioned, is the stan-

dard unit in Fourier analysis, although we are interested in real sinusoids.

Consider the signal x(n) = e

~&~

,n =

0,1,..., JV—1,

where m is a positive

integer. From the DFT definition, we get

N-l N-l

X{k)= J2e

e-^

Y,e~

j¥{k

m)n

0,l,...,N-1

n=0 n=0

Due to the orthogonality property, we get

ran

<S>

N5(k - m) and e~^

o NS(k - (TV - m))

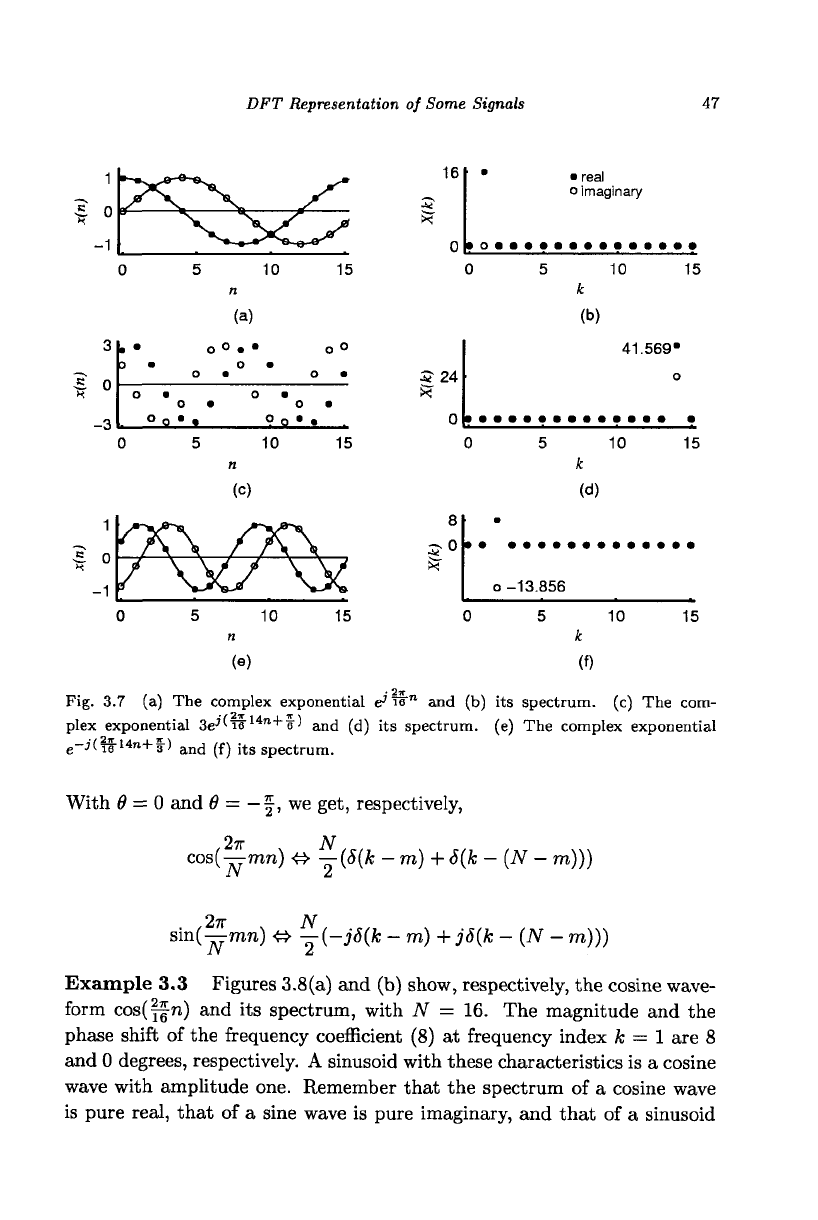
Example 3.2 Figures 3.7(a) and (b) show, respectively, the waveform

if"" and its spectrum, with N = 16. This is a complex exponential with

frequency index one and amplitude one and, therefore, its spectrum consists

of an impulse at frequency index k

—

1 with amplitude sixteen.

Figures 3.7(c) and (d) show, respectively, the waveform 3e

(it

14n+

e) =

ii?-i4n

d its spectrum. This is a complex exponential with frequency

index 14 and complex amplitude 3e

t. Therefore, its spectrum consists

of an impulse at frequency index A; = 14 with amplitude (3)(16)(cos | +

jsin|) = 24(V3 + jl).

Figures 3.7(e) and (f) show, respectively, the waveform

^it

te^ie"

™ and its spectrum. This is a complex exponential with fre-

quency index —14 and complex amplitude e

^. Therefore, its spectrum

consists of an impulse at frequency index k = 16

—

14 = 2 with amplitude

16(cos(-f)+jsin(-f))=8(l-jV3). I

The real sinusoid

The DFT of a real sinusoid, x(n) = cos(^mn + 9), n =

0,1,...,

- 1, is

obtained by expressing it as a combination of complex sinusoids as

x(n) = h

e^e"^"

From previous results for the complex exponentials, we get

cos(-jj-mn + 6)& -^{e

S(k - m) + e-

S(k - (TV - m)))

DFT Representation of Some Signals

• real

o imaginary

10 15

I °

-3

(a)

•

g o •»

10 15

(b)

41.569'

10 15

(c)

(d)

o -13.856

(e)

Fig. 3.7 (a) The complex exponential e'TB"™ and (b) its spectrum, (c) The com-

plex exponential 3e

''i6'

14n

+6') and (d) its spectrum, (e) The complex exponential

-j'Cif-i4n+f)

and

^ its spectrum.

With 0 = 0 and 0 = -|, we get, respectively,

27T N

cos(—mn) •£> —(6(k -m) + 6(k - (N - m)))

2TT N

sin(—mn) ^ —

(-jS(k

- m) + jd{k - (N - m)))

Example 3.3 Figures 3.8(a) and (b) show, respectively, the cosine wave-

form cos(ffn) and its spectrum, with N = 16. The magnitude and the

phase shift of the frequency coefficient (8) at frequency index

= 1 are 8

and 0 degrees, respectively. A sinusoid with these characteristics is a cosine

wave with amplitude one. Remember that the spectrum of a cosine wave

is pure real, that of a sine wave is pure imaginary, and that of a sinusoid

The Discrete Fourier Transform

-1

10 15

• real

o imaginary

10 15

(a)

-8L

(b)

10 15

1 . •

-1

(c)

•6.928

(d)

10 15

(e)

(f)

Fig. 3.8 (a) The sinusoid cos(^n) and (b) its spectrum, (c) The sinusoid sin(^2n)

and (d) its spectrum, (e) The sinusoid cos(||44n 4- |) and (f) its spectrum.

other than a cosine or sine consists of both real and imaginary parts.

Figures 3.8(c) and (d) show, respectively, the sine waveform sin(f|-2n)

and its spectrum. The magnitude and the phase shift of the frequency co-

efficient (-J8) at frequency index k

—

2 are 8 and -f radians, respectively.

A sinusoid with these characteristics is a sine wave with amplitude one.

Figures 3.8(e) and (f) show, respectively, the sinusoid cos(^f 14n + f)

and its spectrum. The magnitude and the phase of the frequency coefficient

(6.9282 - j4) at frequency index k = 2 are 8 and -f radians, respectively.

This is a sinusoid with amplitude one and phase

—

f radians. There are

two points to observe: (i) a real sinusoid with frequency index in the second

half of the frequency range cannot be distinguished from a sinusoid with a

corresponding frequency in the first

half,

as mentioned in Section 2.2, and

(ii) the phase shift is negated. The sinusoid yields a spectrum that is the

same as that of cos(f|2n

—

|). I

DFT Representation of Some Signals

0.9619

0.8536

0.6913

0.5

0.3087

0.1464

0.0381

10 15

(a)

(b)

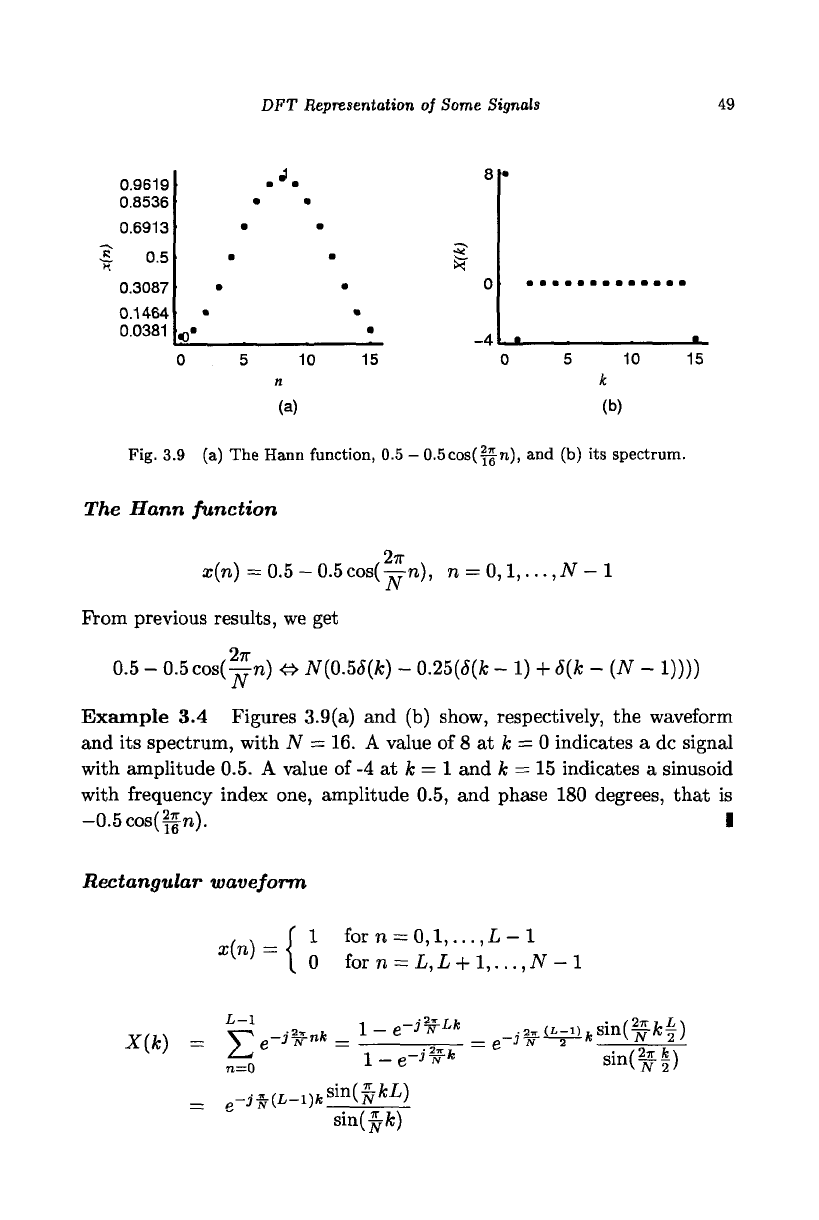
Fig. 3.9 (a) The Hann function, 0.5

0.5cos(^n), and (b) its spectrum.

The Hann function

x(n)

0.5-0.5cos(—n),

0,1,..

.,N - 1

From previous results, we get

0.5

0.5 cos(—n)

N(0.56(k)

0.25(<5(fc

6(k

- (N -

1))))

Example 3.4 Figures 3.9(a) and (b) show, respectively, the waveform

and its spectrum, with

N =

16. A value of 8 at

0 indicates

dc signal

with amplitude 0.5. A value of -4 at

1 and

15 indicates

sinusoid

with frequency index one, amplitude 0.5, and phase 180 degrees, that

-0.5cos(ffn).

Rectangular waveform

x(n)

forn

0,l,...,L-l

{ 0

for

n =

L, L + 1,...,

N - 1

L-\

X(k)

= £\

-J¥nk

l-e~^

_^(-li

sin(ffcf)

n=0

J N

sin(^|)

sin(ffc)

The Discrete Fourier Transform

"sr

ok . . ••••

0 10 20 30

(a)

, ««

0 10 20 30

(c)

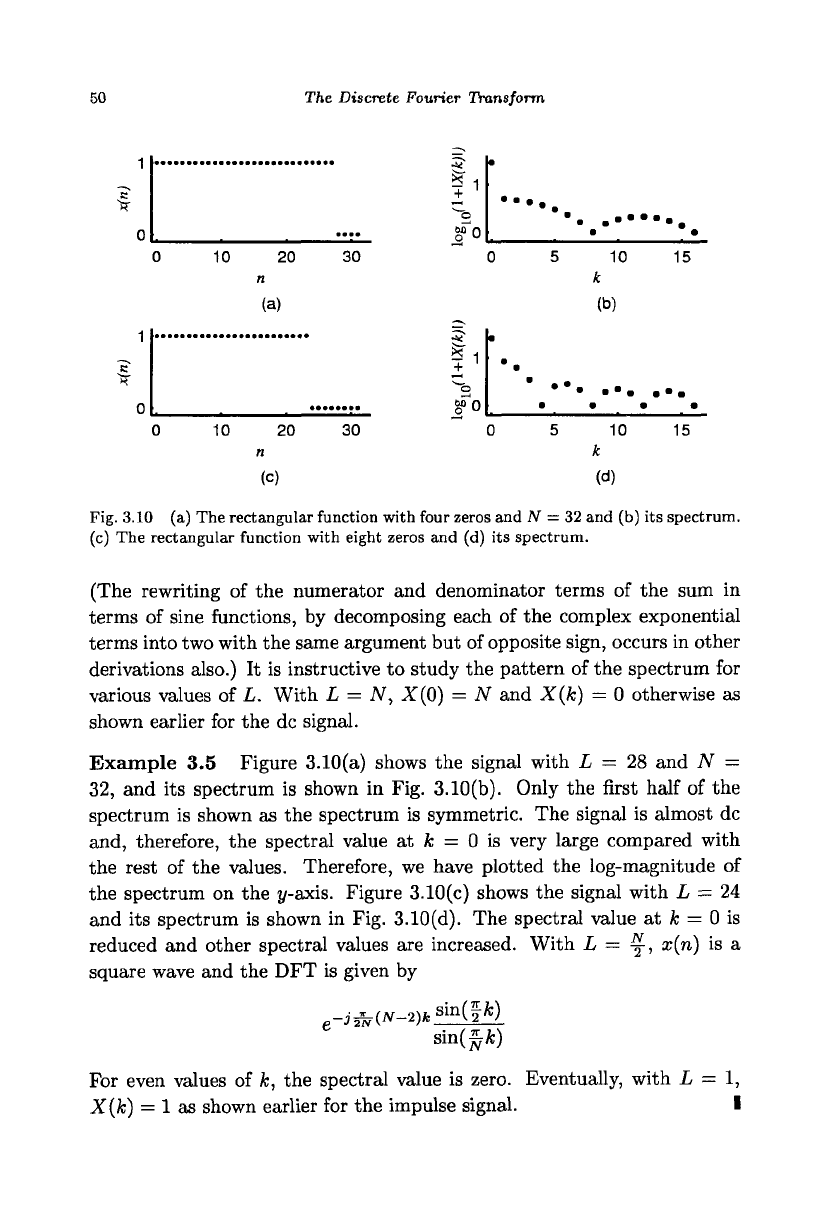
Fig. 3.10 (a) The rectangular function with four zeros and N = 32 and (b) its spectrum.

(The rewriting of the numerator and denominator terms of the sum in

terms of sine functions, by decomposing each of the complex exponential

terms into two with the same argument but of opposite sign, occurs in other

derivations also.) It is instructive to study the pattern of the spectrum for

various values of L. With L = N, X(0) = N and X(k) — 0 otherwise as

shown earlier for the dc signal.

Example 3.5 Figure 3.10(a) shows the signal with L = 28 and N =

32,

and its spectrum is shown in Fig. 3.10(b). Only the first half of the

spectrum is shown as the spectrum is symmetric. The signal is almost dc

and, therefore, the spectral value at k = 0 is very large compared with

the rest of the values. Therefore, we have plotted the log-magnitude of

the spectrum on the

y-axis.

Figure 3.10(c) shows the signal with L = 24

and its spectrum is shown in Fig. 3.10(d). The spectral value at

= 0 is

reduced and other spectral values are increased. With L = %, x(n) is a

square wave and the DFT is given by

-J.^(JV-2)fe

Sln

)

sin(^)

For even values of k, the spectral value is zero. Eventually, with L = 1,

X(k) = 1 as shown earlier for the impulse signal. I

5 10

(b)

5 10

(d)

Direct Computation of the DFT

3.4 Direct Computation of the DFT

In this section, we analyze the computational burden in computing the

DFT from its definition and study the details of the direct implementation.

Example 3.6 Compute the DFT of the 4-point sequence

{2,3,1,4}.

Compute the ID FT of the transform to get back the time-domain data.

Solution

X(k) =

Y^x{n)Wf,

fc = 0,l,2,3

n=0

X(0) = 2x1 + 3x1 + 1x1 + 4x1 = 10

X(l) = 2x

3 x

(-j)

(-l)

j = l

X(2) = ' 2x

3 x

(-l)

lx 1

4 x

(-l)

= -4

X(3)

2xl

3xj

lx(-l)

4x(-j)

l-jl

The IDFT gives the original input samples.

x(n) =

-Y^X(k)W^

n = 0,l,2,3

fc=0

x(0) = J(10x l + (l + jl) x l + (-4)xl + (l-jl)x 1) = 2

x(l) = i(10xl + (l + jl)xj + (-4)x(-l) + (l-jl)x(-j))=3

x{2) = i(i0xl + (l + jl)x(-l) + (-4)xl + (l-jl)x(-l)) = l

ar(3) = i(10xl + (l + jl)x(-j) + (-4)x(-l) + (l-jl)xj)=4l

For the computation of N frequency coefficients, N

complex multiplica-

tions and N(N

—

1) complex additions are required. Therefore, the com-

putational complexity of the direct DFT computation is

0(N

Direct implementation of the DFT

Although, most of the times, we would be using fast algorithms to compute

the DFT, we may have to compute the DFT directly from the definition

at times. We can verify the output of the fast algorithms when they are

The Discrete Fourier Transform

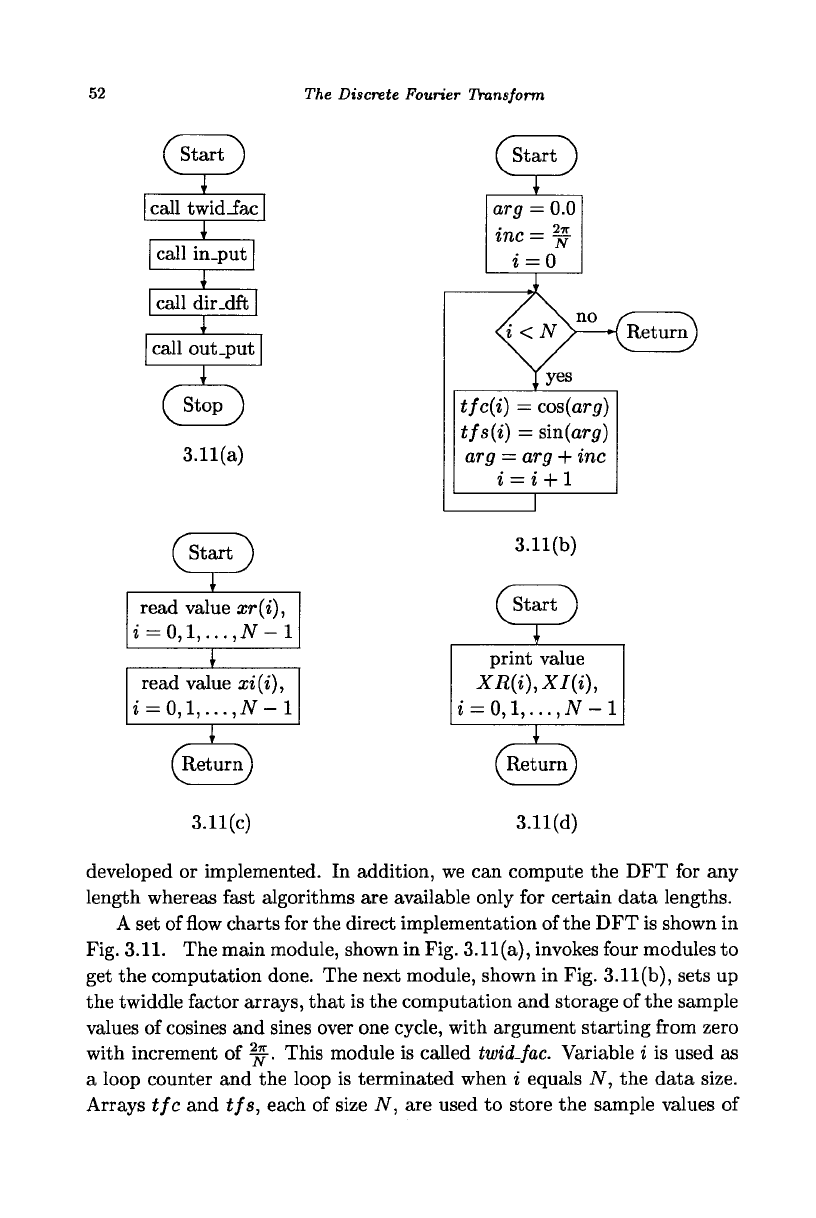
M3tartJ

call twid_fac

call in_put

call dir.dft

call out.put

f Stop ")

3.11(a)

(start)

read value

xr(i),

i =

0,l,...,N-l

read value

xi(i),

i =

0,l,...,N-l

( Return)

3.11(c)

f Start *)

arp = 0.0

2TT

* = 0

•(Return J

tfc(i)

—

cos(arg)

tfs(i) = sin(arg)

arg = arg + inc

i = i + l

3.11(b)

("start J

print value

XR(i),XI{i),

i =

0,l,...,N-l

(Return J

3.11(d)

developed or implemented. In addition, we can compute the DFT for any

length whereas fast algorithms are available only for certain data lengths.

A set of flow charts for the direct implementation of the DFT is shown in

Fig. 3.11. The main module, shown in Fig. 3.11(a), invokes four modules to

get the computation done. The next module, shown in Fig. 3.11(b), sets up

the twiddle factor arrays, that is the computation and storage of the sample

values of cosines and sines over one cycle, with argument starting from zero

with increment of ^. This module is called twid-fac. Variable i is used as

a loop counter and the loop is terminated when i equals N, the data size.

Arrays tjc and tjs, each of size N, are used to store the sample values of

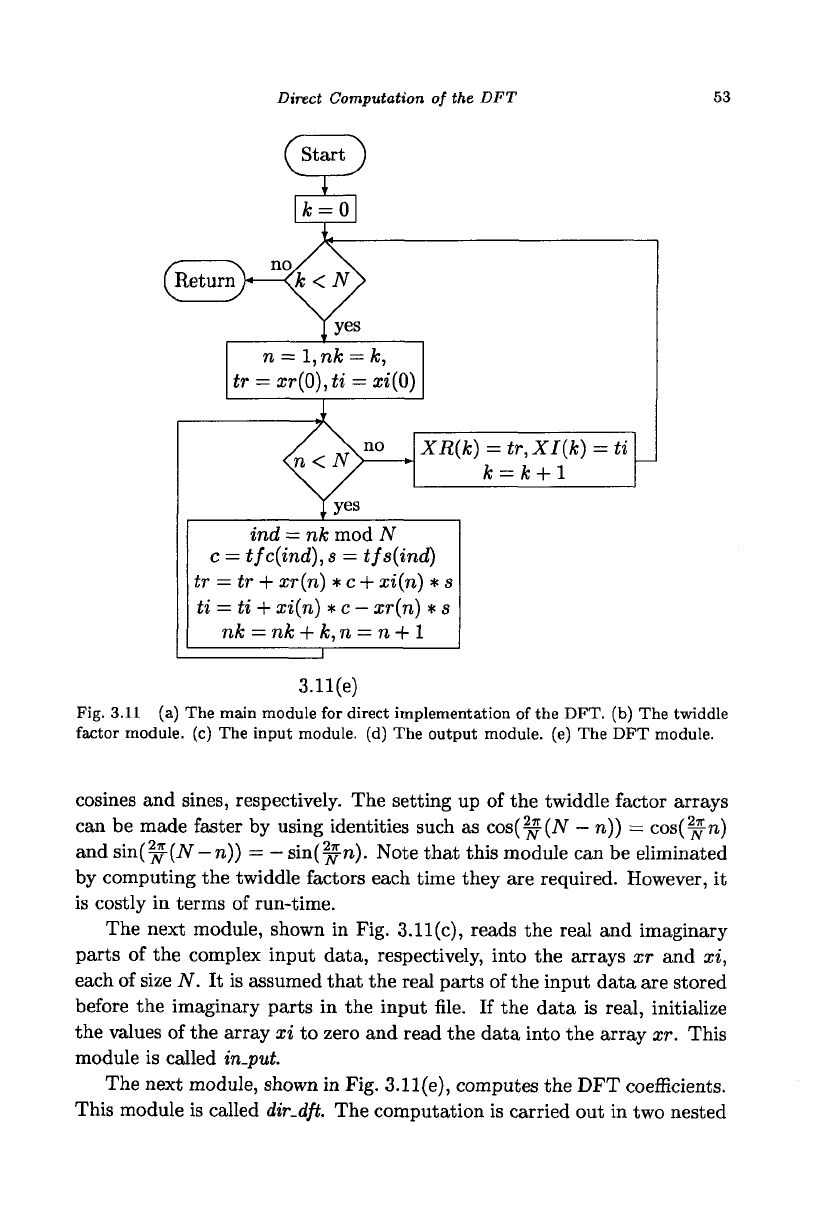
Direct Computation of the DFT 53

(Start)

k = 0

• N no/ \

Return)* (k < JV>

Iyes

n = l,nk = k,

tr = xr(0),ti = xi(Q)

XR(k) = tr,XI(k) = ti

k = k + l

ind

—

nk mod N

c = tfc(ind), s = tfs(ind)

tr = tr + xr(n) * c + xi(n) * s

ti = ti + xi(n) * c

—

xr(n) * s

nk = nk + k,n = n + 1

3.11(e)

Fig. 3.11 (a) The main module for direct implementation of the DFT. (b) The twiddle

factor module, (c) The input module, (d) The output module, (e) The DFT module.

cosines and sines, respectively. The setting up of the twiddle factor arrays

can be made faster by using identities such as cos(^(iV

—

n)) = cos(^n)

and sin(^(iV-7j)) = - sin(^n). Note that this module can be eliminated

by computing the twiddle factors each time they are required. However, it

is costly in terms of run-time.

The next module, shown in Fig. 3.11(c), reads the real and imaginary

parts of the complex input data, respectively, into the arrays xr and xi,

each of size N. It is assumed that the real parts of the input data are stored

before the imaginary parts in the input file. If the data is real, initialize

the values of the array xi to zero and read the data into the array xr. This

module is called in-put.

The next module, shown in Fig. 3.11(e), computes the DFT coefficients.

This module is called dir-dft. The computation is carried out in two nested