Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

244

Aliasing and Other Effects

Reduction of leakage

To reduce leakage, the natural solution is to use an appropriate record

length, if possible. Similar to the case of the aliasing problem, prior knowl-

edge of a signal will enable to fix the record length or a trial and error

procedure can be used, keeping the sampling interval fixed. Otherwise,

leakage can be reduced at the expense of increased smearing of the spec-

trum by the application of windows. As mentioned earlier, if there is no

leakage or negligible leakage then choose the rectangular window. Other-

wise choose any of the other windows that reduces the side lobes to the

desired level. Windows can be applied in the time-domain by multiplying

the data, x(n), with window samples, w(n). That is, instead of comput-

ing the DFT of x(n), we compute the DFT of x(n)w(n). Note that the

window w(n) must be centered on the truncated signal x{n) in the defined

interval of x(n), wherever it may be on the time scale. Windows can also

be applied, in the frequency-domain, in terms of the frequency coefficients

of the rectangular window. Although our discussion concentrated on the

truncation problem in the time-domain, it should be noted that windows

can be used in both the time- and frequency-domains.

11.3 Picket-Fence Effect

In this section, we consider the appropriate frequency spacing or increment

for the unique representation of a signal. The theory of Fourier analysis is

that the frequency increment between the harmonic components must be

the reciprocal of the period of the waveform under analysis. Here again, we

run into a problem because we tend to violate the theory by not provid-

ing proper frequency spacing (because of not using a long enough record

length), in order to make the problem suitable for numerical analysis.

The DFT coefficients specify the spectrum only at certain frequencies.

The computation of the coefficients at these frequencies is carried out ex-

actly the same way whether a signal is periodic or not. For periodic signals,

with input samples taken over an integral number of periods, the frequency

increment is correct. If we assume that the signal is periodic, then the spec-

trum of the signal shown in Fig. 11.12(a) is just the dc component as shown

in Fig. 11.12(b). If we mean that the same set of samples represents an

aperiodic signal, then its spectrum is continuous. The DFT coefficients are

only a finite set of samples of the continuous spectrum, even if it is band-

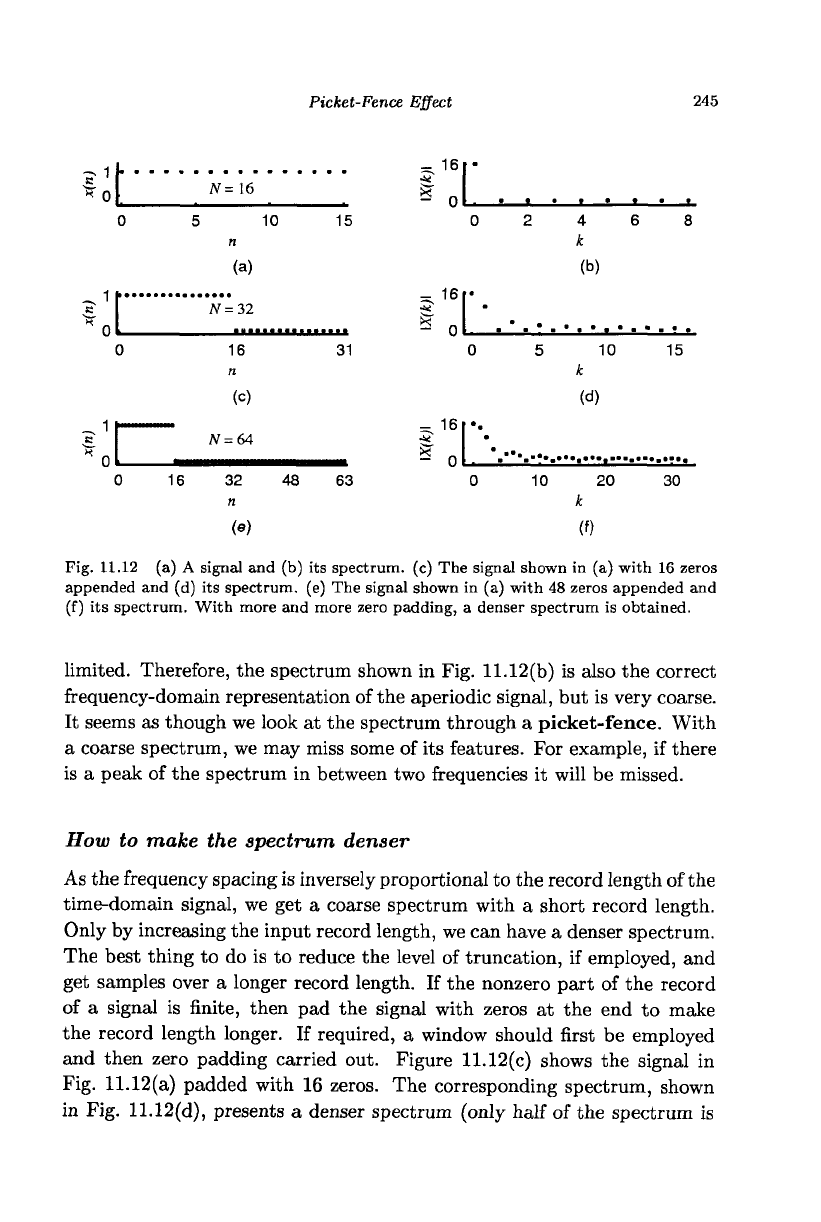
Picket-Fence Effect

245

16 i

* 0

_ 1

N=16

(a)

W = 32

(c)

<•)

}

16 *

•

16 *

•

• •

(b)

(d)

•

. • .

Fig. 11.12 (a) A signal and (b) its spectrum, (c) The signal shown in (a) with 16 zeros

appended and (d) its spectrum, (e) The signal shown in (a) with 48 zeros appended and

(f) its spectrum. With more and more zero padding, a denser spectrum is obtained.

limited. Therefore, the spectrum shown in Fig. 11.12(b) is also the correct

frequency-domain representation of the aperiodic signal, but is very coarse.

It seems as though we look at the spectrum through a picket-fence. With

a coarse spectrum, we may miss some of its features. For example, if there

is a peak of the spectrum in between two frequencies it will be missed.

How to make the spectrum denser

As the frequency spacing is inversely proportional to the record length of the

time-domain signal, we get a coarse spectrum with a short record length.

Only by increasing the input record length, we can have a denser spectrum.

The best thing to do is to reduce the level of truncation, if employed, and

get samples over a longer record length. If the nonzero part of the record

of a signal is finite, then pad the signal with zeros at the end to make

the record length longer. If required, a window should first be employed

and then zero padding carried out. Figure 11.12(c) shows the signal in

Fig. 11.12(a) padded with 16 zeros. The corresponding spectrum, shown

in Fig. 11.12(d), presents a denser spectrum (only half of the spectrum is

246

Aliasing and Other Effects

shown since it is symmetric). With more and more zero padding, we get a

denser spectrum as shown in Figs. 11.12(e) and (f). The signal shown in

Fig. 11.12(e) is a more accurate representation of the given aperiodic signal

than that shown in Fig. 11.12(c).

A periodic signal is composed of components with frequencies which are

integral multiples of its frequency and of no other. Therefore, we should set

the record length equal to an integral number of cycles and there should be

no zero padding. If

truncate a periodic signal, we are making an analysis

with a false period. An aperiodic signal is composed of components of all

frequencies. Whether we truncate an aperiodic signal or not, the frequency

coefficients computed by DFT are part of the spectrum. The point is that

the signal processed by the DFT should be sufficiently close to the actual

signal, with the appropriate selection of the record length and the number

of samples so that the aliasing and leakage errors are small enough and the

spectrum is sufficiently denser.

11.4 Summary and Discussion

• In this chapter, we studied the aliasing, leakage, and picket-fence

effects. These effects occur, in the analysis of a signal, due to the

setting of parameters such as record length, sampling interval, and

frequency spacing not in accordance with the theory of the Fourier

analysis, in order to use the DFT. It is normal that the DFT solu-

tion is not exact as the solution given by analytical method. But,

the analytical method is almost impossible to use with practical

signals. What is important is to ensure that the error in DFT rep-

resentation is within the required limits. Fortunately, we can reduce

the errors to any desired level by increasing the number of samples

and/or the record length and using other techniques presented.

• Noting that DFT means the same computation at any time, the

accuracy control lies in the data modeling. Although sampling and

truncation are unavoidable to analyze a signal using the DFT, the

user has to ensure that the digital signal is sufficiently close to the

actual signal to keep the errors within tolerable limits. Therefore,

if the DFT of a signal seems to be in gross error it is because of im-

proper data modeling, such as insufficient sampling rate, too much

of truncation, insufficient number of bits to represent data values,

Exercises

247

etc.

The situation is like using a computer to solve a problem. A

computer executes some instructions in a predefined way. If the

execution of a program yields improper output, the reason is either

the programmer not putting up the proper algorithm, or proper

codes according to the language used, or proper input data.

• In the next two chapters, we describe the approximation of the

continuous-time Fourier series and Fourier transform of signals and

provide examples illustrating the effects described in this chapter.

Reference

(1) Brigham, E. O. (1988) The Fast Fourier Transform and Its Appli-

cations, Prentice-Hall, New Jersey.

Exercises

11.1 What is the minimum number of samples in a period required to avoid

aliasing. What are the DFT coefficients. Find the DFT coefficients with 4,

8, 16, and 32 samples in a period.

(a) x(t) = -4sin(107ri)

(b) x(t) = cos(107ri)

* (c)x(t) = 2cos(147rt)

(d) x(t) = 5sin(167rt)

(e) x(t) =3cos(327it)

(f) x(t) =4sin(127rt)

(g) x(t) =2cos(24?ri)

(h) x(t) = -3

11.2 With JV = 8 and L = 8, list the DFT coefficients of the signal using

the rectangular, triangular, Hann, and hamming windows.

(a) x(n) = cos(^2n)

* (b) x(n) = cos(^2.5n)

* 11.3 The frequency of the significant highest possible frequency com-

ponent of an aperiodic signal of record length 0.1 seconds is 5 kHz. A

minimum frequency increment of 20 Hz is required. Determine the number

of samples required to approximate the spectrum using the DFT. Is zero

248

Aliasing and Other Effects

padding required? If so, what is the minimum record length required?

11.4 The frequency of the significant highest possible frequency component

of an aperiodic signal of record length 0.1 seconds is 12.5 kHz. A minimum

frequency increment of 5 Hz is required. Determine the number of sam-

ples required to approximate the spectrum using the DFT. Is zero padding

required? If so, what is the minimum record length required?

Programming Exercises

11.1 Write a program to apply the Hann window to a signal, with L = JV'.

11.2 Write a program to apply the hamming window to a signal, with

L = N.

11.3 Write a program to apply the triangular window to a signal, with

L = N.

Chapter 12

The Continuous-Time Fourier Series

The FS is the frequency-domain representation of a continuous-time peri-

odic signal in terms of an infinite set of harmonically related sinusoids in

addition to a dc value. Both the DFT and the FS do the same function,

that is, providing the sinusoidal representation of signals. However, the

DFT analyzes a discrete signal whereas the FS analyzes a continuous-time

signal. Therefore, the essential differences to be considered in approximat-

ing the FS coefficients by those of the DFT are: (i) the integral evaluated

in the case of the FS is approximated by a numerical integration procedure

and (ii) a finite set of coefficients is used in DFT and an infinite set of

coefficients is used in FS.

In Sec. 12.1, we start with the two forms of the definitions of the 1-D FS,

describe the Gibbs phenomenon, present the relation between the DFT and

the FS, and conclude with an example of approximating the FS coefficients

by those of the DFT. In Sec. 12.2, we describe the approximation of the

2-D FS coefficients by those of the DFT.

12.1 The 1-D Continuous-Time Fourier Series

The FS represents a continuous-time periodic signal, x(t), with period T

as a sum of an infinite set of harmonically related sinusoids in addition

to a dc value. The frequency of the fundamental harmonic is

u>o

= ^.

The frequencies of the other harmonics are integral multiples of w

. The

sufficient conditions, called Dirichlet conditions, a signal should satisfy so

that it can be represented by a Fourier series are: (i) the signal x(t) has an

absolutely convergent integral, that is /

|x(t)|di < oo, (ii) the signal has

249

250

The Continuous- Time Fourier Series

a finite number of maxima and minima in one period, and (iii) the signal

has a finite number of finite discontinuities in one period. These conditions

are met by most signals of practical interest.

The trigonometric form

A real periodic signal, x(t), satisfying Dirichlet conditions, can be equiva-

lently expressed in terms of cosine and sine waveforms as

x(t) = X

(0) +

Y^(X

(k)

cos(k(j

t) + X

(k) sm(kuj

t)), (12.1)

where

1 /Tl-t-i

Xc(0) =

J x(f)dt,

o rti+T

(k)

= — I x(t) cos(fcw

*) dt, k =

1,2,...,

T Jti

ti+T

{']

'" . ~ ", ' ~.~. ,oo

tl+T

X„(k) = — x(t) sm(kcj

t) dt, k=l,2,...,oo

and ti is arbitrary.

The exponential form

As in the case of the DFT, it is more efficient to represent a sinusoid in

terms of complex exponentials. Substituting the fact that

jk<jj

t i

—jkwot

Jkuiot _

—jku>ot

cos(ku>ot)

— and sin(kuiot) =

into Eq. (12.1), we get

jkuot _i_

p—jkuiot

pjkuot _

—jkuot

x(t) = X

(0) + ]T(X

(fc)- \ + *.(*) a )

fc=i

Rearranging the terms, we get

*(*)

fv^W-^W

c(k)

(k)

jkuot)

k=l

The 1-D Continuous-Time Fourier Series 251

Let

(0)

(0),

(k)

= *°W-/M*>, and

(-k)

= *°W+J'*-W.

Note that X

(fc) and X

(—fc) are complex conjugates, and X

{k) =

2Re(X

(k)) and X

(k) = -21m(X

(k)). Now, x(t) can be expressed

x(t) =

(0)

+ £(X

(A;)e

+ X„ (-*)e-'

*>«)

By allowing the summation index, k, to run from — oo to oo, we can rewrite

the equation as

x(t) = J2

cs(k)e

(12.2)

fc= — oo

We use the denning equations for X

(k) and X

(k) to get

(k)

1 /-

tl+T

cs(k) = = / 2;(i)(cos(fcw

i) - jsin(fcw

i))^,

1 /"'

1+T

= - / x{t)e-

jkuot

dt, k = -oo,...,

-1,0,1,...,

oo (12.3)

Gibbs phenomenon

The failure of the Fourier representation to provide uniform convergence in

the vicinity of a discontinuity of a signal is called the Gibbs phenomenon.

In the vicinity of a discontinuity, the Fourier representation deviates at the

least about 9% from the original signal irrespective of the number of coeffi-

cients used. It is not surprising since it is impossible to provide a pointwise

match in the vicinity of a discontinuity with a set of basis functions each

of those is continuous. Where there is no discontinuity, by increasing the

number of frequency coefficients to represent a signal, the Fourier represen-

tation can be made to correspond to the original signal to any tolerance.

Let us assume that we are approximating a signal using only part of its

spectrum (2JV+1 complex frequency coefficients). The part of the spectrum

used can be considered as obtained by multiplying the original spectrum by

a rectangular window whose value is unity during the part of the spectrum

used and zero otherwise. This multiplication operation in the frequency-

domain is equivalent to convolution of the corresponding signals in the

time-domain. Now, we are going to derive the convolution expression that

252

The Continuous-Time Fourier Series

will help us to understand the characteristics of the reconstructed signal.

The FS synthesis expression with 2iV + 1 coefficients is given by

k=-N

Replacing

(k)

by its definition and interchanging the order of summation

and integration, we get

*N(t)

= i f x(l) J2 e

»°Wdl

1 Jo

k=-N

Let us evaluate the summation operation separately.

jkuj

{t-i)

k=-N

j(k-N)w

(t-i)

k=0

i(2iV+l)wo(t-0

-jNw

{t-l)_

sin(

(2N+l)u

{t-l)

)

—

Juo(t-l)

sin(^i)

Now, the convolution expression characterizing the reconstructed signal

using only 2N + 1 coefficients is given by

(t) =

±j\(l)

sin(

(2Af+iHft-i?

)

n(i-2^1)

i r

= - / x(l)xs(t - l)dl

The reconstructed signal using 27V + 1 coefficients is the result of the con-

volution of the original signal x(l) and the sine function

xs(l).

The sine

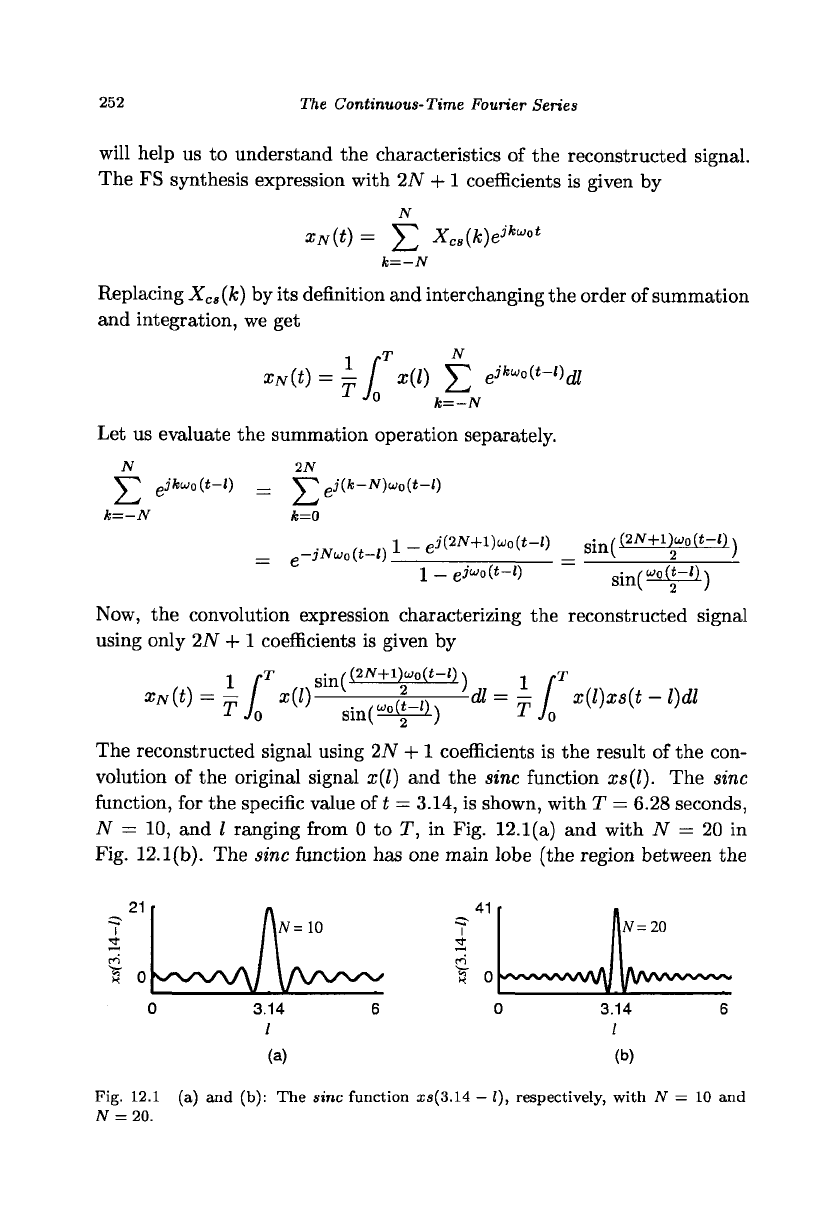
function, for the specific value of t = 3.14, is shown, with T = 6.28 seconds,

N = 10, and I ranging from 0 to T, in Fig. 12.1(a) and with N = 20 in

Fig. 12.1(b). The sine function has one main lobe (the region between the

(a)

(b)

Fig. 12.1 (a) and (b): The sine function is(3.14

—

I), respectively, with N = 10 and

= 20.

The 1-D Continuous-Time Fourier Series

253

(a)

(b)

Fig. 12.2

(a) and

(b): The reconstructed square wave with JV

= 10

and JV

= 20,

respectively.

two adjacent zero crossings about

/ =

3.14) and large number of side lobes

(the other regions between adjacent zero crossings), which are alternately

positive and negative. The total area of the sine function during

period

for any value of JV since

gifc-oC*-*)

f (l + 2cos(wo(t-0)

k=-N

cos(2cj

I)) +

• • •

cos(Noj

I))) dl

= /

dl =

An inspection

the figures shows that the total area

the side lobes

pointing downwards is more than that of the side lobes pointing upwards.

To compensate for this, the area of the main lobe is more than T. The result

of this is that the synthesized signal exhibits at the least about 9% deviation

discontinuity of the signal. Figures 12.2(a) and (b) show, respectively,

the Fourier synthesis of

square wave with

N =

10 and JV

20. As the

number of coefficients is increased, the amplitude of the deviation reaches

finite limit since the ratio between the amplitudes of the main and side lobes

reaches

finite limit, but the frequency of the oscillations increase. This

behavior is different from that of the other parts of the signal, where there

is no discontinuity,

that the match between the signal and its Fourier

synthesis improves as the number of coefficients is increased.

The relation between

the

DFT and the

Let

approximate the integral

Eq. (12.3) using the rectangular rule

of numerical integration. We divide the period

into JV intervals, each

of those

is of

width

= ^,

and represent the signal

JV points