Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications
Подождите немного. Документ загружается.

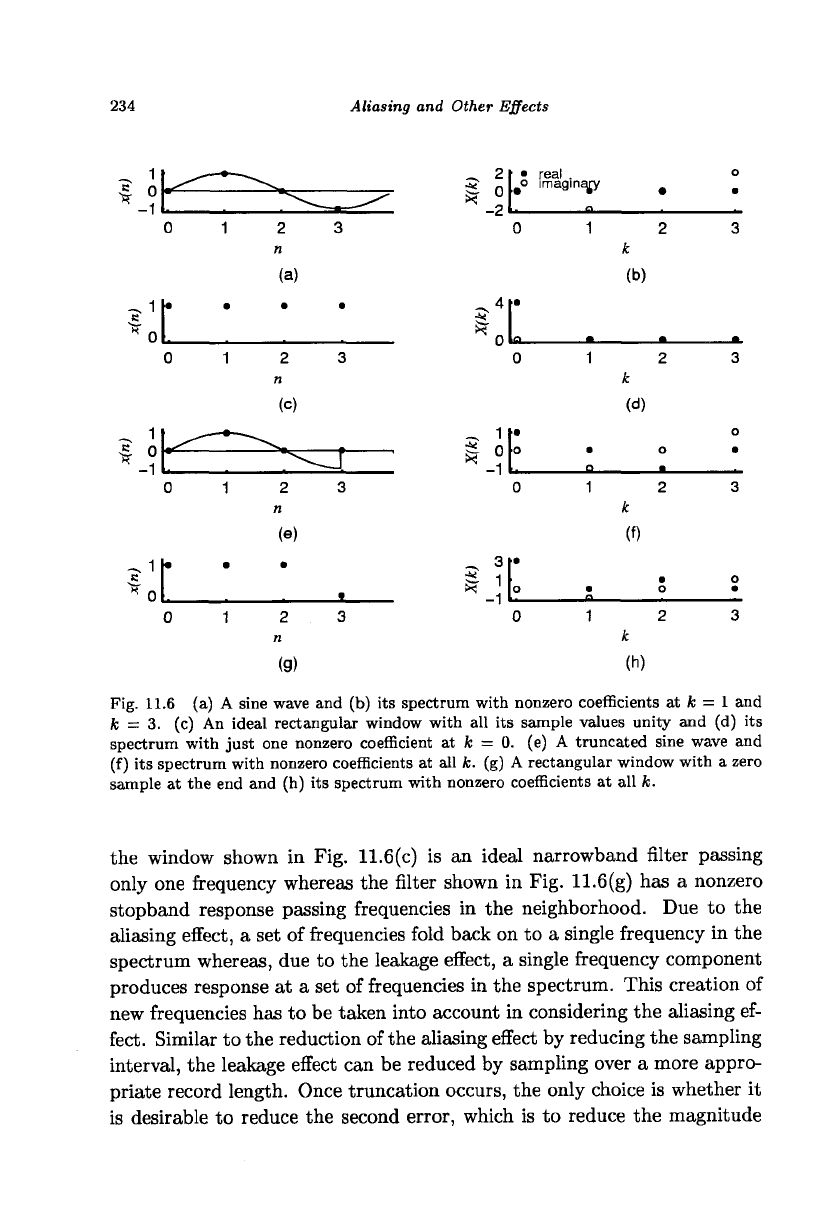
234 Aliasing and Other Effects
=
1
2
n
(a)
_ 2
-*
X
1
• real .
o imaginary
(b)
(c)
(e)
1
0
-1
(d)
(0
(g)
(h)
Fig. 11.6 (a) A sine wave and (b) its spectrum with nonzero coefficients at k = 1 and
k = 3. (c) An ideal rectangular window with all its sample values unity and (d) its
spectrum with just one nonzero coefficient at k = 0. (e) A truncated sine wave and
(f) its spectrum with nonzero coefficients at all k. (g) A rectangular window with a zero
sample at the end and (h) its spectrum with nonzero coefficients at all k.
the window shown in Fig. 11.6(c) is an ideal narrowband filter passing
only one frequency whereas the filter shown in Fig. 11.6(g) has a nonzero
stopband response passing frequencies in the neighborhood. Due to the
aliasing effect, a set of frequencies fold back on to a single frequency in the
spectrum whereas, due to the leakage effect, a single frequency component
produces response at a set of frequencies in the spectrum. This creation of
new frequencies has to be taken into account in considering the aliasing ef-
fect. Similar to the reduction of the aliasing effect by reducing the sampling
interval, the leakage effect can be reduced by sampling over a more appro-
priate record length. Once truncation occurs, the only choice is whether it
is desirable to reduce the second error, which is to reduce the magnitude

Leakage Effect
235
of the new frequency components produced at the cost of increasing the
first error, the smearing of the spectrum. To study this choice, we have to
understand the properties of various windows.
Before we do that, let us look at another truncation model. It is to
reduce the record length we truncate a signal. Therefore, if the spectrum
is sufficiently dense, we can compute the spectrum of the nonzero part of
a signal after truncation. In the truncation model presented so far, we
assumed that the signal is sampled correctly and the window is imperfect.
In computing the DFT of the nonzero part of a truncated signal, we assume
that the window is perfect and the signal is not sampled over an integral
number of cycles.
The frequency response of the DFT
The DFT of the complex sinusoid, x{n)
—
e-
7
"^"', is given by
X{k) =
jS^'e-^"*
n=0
JV-1
n=0
I -
e
-J^-(k-l)N
l-e-i^-(k-i)
=
sirnr(fc-Q
fa(1
_j,
K>
_
n
sin £(*;-/)
If I is an integer, the sinusoid completes an integral number of cycles in
the period N and we get an impulse at the corresponding frequency index
properly representing the sinusoid. If I is not an integer, the sinusoid does
not complete an integral number of cycles in the period N and, as a result,
it is represented not as a sinusoid at a single frequency but as a combination
of a number of sinusoids those have bins. The energy of a sinusoid, in this
case,
is leaked to neighboring frequencies. The set of narrowband filters,
the DFT, does not have a sharp response for frequency components at other
than bin frequencies and has a worst response for frequency components
with frequencies at the midpoint between bins.

236
Aliasing
and
Other Effects
1
0.08
0
o
8$
M
° +
•
o 9 r
+
..
+ -*•
«
»
9
"
«
x
9
>
9
"
8
X
8
" •
rectangular
+
o
hamming
+ Hann
x triangular
X
® 9
9
X
9
X
9
L--
8
*
0
+
=
32
=
32
5
n
+
"?,
0
4 8 12 16 20 24 28 32
n
Fig.
11.7
Time-domain representation
of
different windows.
Windows
Rectangular window
The rectangular window
is
denned
as
...
f 1 for n
—
0,1,..
.,L
—
1
rect
w
(n)
= \
[0
for n = L,L + 1,...,N - 1
The time-domain representation
of
this window
is
shown
in Fig. 11.7
with
L
= 32 and
TV
= 32. The DFT of
this window, with
u = ^, is
given
by
The magnitude
of the DFT of
this window
is
shown
in Fig.
11.8(a) with
L
= 16 and N = 64. The
magnitude
of the
largest side lobe
is
-13.339
dB
(slightly greater than one-fifth
of the
main lobe magnitude).
The
response
to complex sinusoids
is the
same
as
given
in the
last subsection, which
can
be obtained
by
replacing
k = k
—
I and N = L in Eq.
(11-1).
The
function
in
Eq.
(11.1)
has a
value
of L at k = 0. X(k) = 0 for
A;
= £,
^,.... Main
lobe width
is ^.
Side lobe width
is ^.
Apart from
k = 0,
peaks occur
at
k
= 2T' If'
• • ••
Magnitude
at
peaks
is
given
by
sin
^(
2fc+1
^,fc
= 1,2,.. ..
For large values
of L, the
side lobe peak magnitudes
are
approximately
|^,
2i
a
+ U — 3N_ 5N_
57r
v
• • at ft — 2L
>
2L '
There
are
other windows, some
of
which
we
present
in
this section,
apart from
the
rectangular window which
is
inherent whenever
we
truncate
a signal. These windows
are
smoother
and,
therefore, their spectra have

Leakage Effect
237
0
pa -20
£-40
|-60
-80
rectangular
N
=
64
L= 16
(a)
Harm
L= 16
-32.192
16
(c)
24
0
«-
lu
T3
- -20
o
^-30
J<
* _40
-50
"•» triangular
> N
=
64
\ L=16
\
1
\ ^-25.913
lA ^
\
1
\ /A *•*
\f\ A
II
\t \l \
12 18 24 30
(b)
0
pa -10
§-20
$-30
>3
-40
'•• hamming
*. N = 64
. L=16
•
•
-40.160
••••••«
««••••••••.
0 4 10 16
k
(d)
22 28
Fig. 11.8
Harm, and
(a),
(b), (c), and (d): The magnitude spectrum of the rectangular, triangular,
hamming windows, respectively.
wider main lobe and smaller side lobes. The truncated data is modified by
multiplying it with the window samples so that the sample values of the
modified data is smoothly reduced to zero or near zero at both the beginning
and end of the record. The major advantage of these other windows is the
possibility of detecting a weak frequency component that may be masked by
the large side lobes of the rectangular window. Therefore, the rectangular
window is preferred: (i) if there is no leakage, (ii) if the leakage is within
tolerable limits, or (iii) if leakage can be reduced to tolerable limits by using
a more appropriate record length. The other windows when used with no
leakage or very little leakage leads to the undesirable effect of smearing the
spectrum due to a wider main lobe with no advantage. There are several
windows with different characteristics. A choice has to be made depending
on the requirements.

238
Aliasing and Other Effects
Triangular window
One approach to have smaller side lobes is to multiply the DFT of the
rectangular window by
itself.
This increases the ratio between the main
and side lobe amplitudes at the cost of doubling the main lobe width.
The multiplication of the DFTs results in the convolution of rectangular
windows in the time-domain. The triangular window is defined as
{
\n for n =
0,1,...,
§
tri
w
(L -n) for n = \ + 1, \ +
2,...,
L - 1
0 forn = L,L +
l,...,N-l
The time-domain representation of this window is shown in Fig. 11.7 with
L
—
32 and N = 32. The circular convolution of a rectangular window
red (n)-i
l
^v n = 0,1,. ..,^ - 1
with itself followed by a circular right shift of one position yields the trian-
gular window with a scale factor. For example,
x
r
ect
w
(n) = {1,1,0,0} e> X
rect
„(k) = {2,l-jl,0,l+jl}
L
x
triw
(n + 1) = {1,2,1,0} ^ X?
ect
Jk) = {4,-j2,0,j2}
2
%x
M
„(n) = {0,1,2,1} & X
r
2
erf
Jfc)e-^
fc
= {4,-2,0,-2}
Therefore, the DFT of the triangular window is given in terms of that of
the rectangular window as
2
That is, with u = ^,
2 /sinfrjfcf)
X
^
(fc)
-Z^
sin(
f) )
6 (1L2)
The magnitude of the DFT of this window is shown in Fig. 11.8(b) with
L = 16 and N = 64. The magnitude of the largest side lobe is -25.913 dB.
The response to complex sinusoids is obtained, by replacing k by k
—
I and
N = L in Eq. (11.2), as
2/_sin-V^\
Mk
_
l}
L\smUk-l)

Leakage Effect 239
Let
us
consider
the
reason
for the
differences
in the
spectral behavior
of the
rectangular
and
triangular windows. Because
of
discontinuity, according
to
the
theory
of
Fourier analysis,
the
amplitude
of the
spectrum
of the
rectangular window decreases
at the
rate which
is a
function
of
j,
where
k is
the frequency index. This
is
evident from
Eq.
(11.1)
and
from
Fig.
11.8(a).
With
no
discontinuity,
the
amplitude
of the
spectrum
of the
triangular
window decreases
at the
rate which
is a
function
of -^
•
This
is
evident
from Eq. (11.2)
and
from
Fig.
11.8(b).
In
addition, from
Eqs.
(11.1)
and
(11.2),
we
find that
the
main lobe width
is ^ for the
rectangular window
and
^ for the
triangular window. Therefore,
the
main lobe width
is 8 in
Fig. 11.8(a)
and it is 16 in Fig.
11.8(b).
Hann window
Another approach
to
reduce
the
size
of the
side lobes
of the
rectangular
window
is to
make
the
frequency response
to be the sum of the
scaled
and
shifted responses
of
three rectangular windows
so
that
the
side lobes tend
to cancel
out.
This implies
the
multiplication
of the
rectangular window
by another function
(a
linear combination
of
complex exponentials)
in the
time-domain.
The
multiplication
in the
time-domain results
in the
convolu-
tion
of the
DFTs
of the two
functions
in the
frequency-domain.
The
Hann
window
is
defined
as
hnn rr7-)-
/ 0.5 -
0.5 cos(^n) forn
=
0,l,...,L-l
The time-domain representation
of
this window
is
shown
in Fig. 11.7
with
L
= 32 and N =
32. Since
cos(—n)
= ,
the response
to
complex sinusoids
of
this window
is
given
in
terms
of
that
of
the
rectangular window
as
X
han
„
(*) =
0.5X
rect
„
(k) - 0.25X
rectw
(* + 1) - 0.2bX
rectw
{k
- 1)
The magnitude
of the DFT of
this window
is
shown
in Fig.
11.8(c) with
L
= 16 and N =
64.
The
magnitude
of the
largest side lobe
is
-32.192
dB.
The main lobe width
is 16
samples.

240 Aliasing
and
Other Effects
Hamming window
The hamming window
is
defined
as
'.54
-
0.46cos(^n)
for n =
0,1,...,L
- 1
ham
w
(n)
=
<
v
' { 0 for n = £,£ +
!,...,JV
- 1
The time-domain representation
of
this window
is
shown
in Fig. 11.7
with
L
= 32 and N =
32.
The
response
to
complex sinusoids
of
this window
is
given
in
terms
of
that
of the
rectangular window
as
X
hamw
(k) =
0.54X
rect
„
(*) -
0.23X
rect
„
(k + 1) - 0.23X
rectw
(fc
- 1)
The magnitude
of the DFT of
this window
is
shown
in Fig.
11.8(d) with
L
= 16 and N = 64. The
magnitude
of the
largest side lobe
is
-40.160
dB.
The main lobe width
is 16
samples.
The frequency response
of the
rectangular
and
Hann
windows
The frequency response
of the
rectangular
and
Hann windows
to
complex
exponential,
x{n) =
e-
7
^"', with frequency indices
1.0, 1.3 and 1.5 and
N
= 64 are
given
in Fig. 11.9.
With frequency index
1.0,
there
is no
leakage
and the
response with
the
rectangular window
is
ideal
as
shown
in
Fig.
11.9(a) whereas that with
the
Hann window gives responses
at two
adjacent frequencies also
as
shown
in (b). As can be
seen from
(c),
with
frequency index
1.3, the
response with
the
rectangular window
is
relatively
sharp
but
with
a
large leakage effect. There
is
equal response,
in (e), at
frequency indices
1 and 2 as the
frequency
of the
complex sinusoid
is 1.5,
that
is in
between these frequencies.
As can be
seen from
(d) and (f), the
Hann window provides
a
much reduced leakage
but the
response
is
less
sharp close
to the
frequency
of the
complex sinusoid.
The frequency response
can be
explained
in
terms
of
the sine function.
The
DFT
detects frequency components with integer frequency indices
ex-
actly. That is
the
zero crossings
of
the sine function,
the
frequency response
of
the DFT
shown
by a
continuous curve, occurs
at all the bin
frequencies
except
at the
frequency
of
interest, where
the
peak
of the
main lobe
is the
sample value. With
a
non-integer frequency index,
the
sine function
is
centered
at
that frequency giving nonzero response
at all bin
frequencies.
The difference between
the
continuous response curves
is
that
the
response
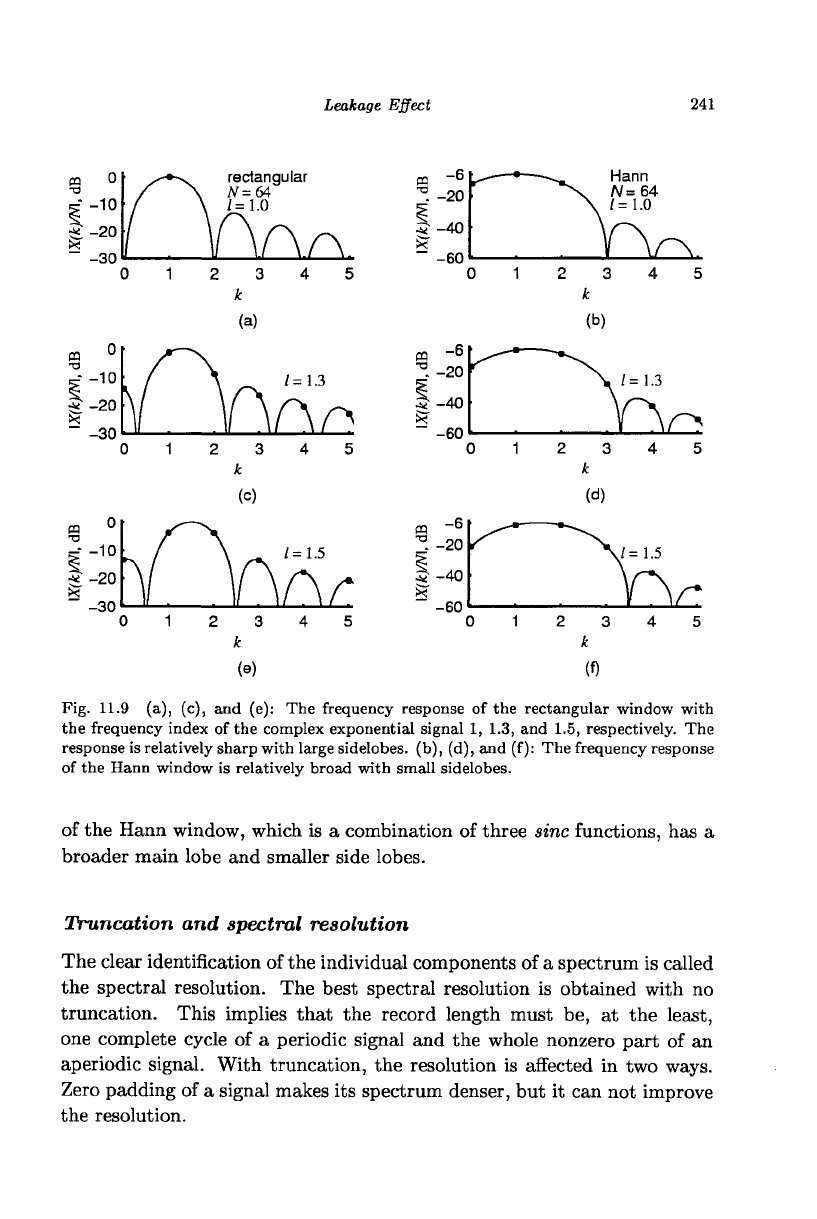
Leakage Effect
241
pa "
£-20
-30
rectangular
W=64
/=1.0
(a)
AAV
2 3
k
(e)
-6
-20
-40
-60
-6
-20
-40
-60
-6
-20
-40
-60
(
3 1
3 1
3 1
2
2
2
Hann
\ W=64
\ /=1.0
Y\n\
3 4 5
k
(b)
^. /=1.3
v\r>
3 4 5
k
(d)
\./=1.5
nr
3 4 5
k
(f)
Fig. 11.9 (a), (c), and (e): The frequency response of the rectangular window with
the frequency index of the complex exponential signal 1, 1.3, and 1.5, respectively. The
response is relatively sharp with large sidelobes. (b), (d), and (f): The frequency response
of the Hann window is relatively broad with small sidelobes.
of the Hann window, which is a combination of three sine functions, has a
broader main lobe and smaller side lobes.
Truncation and spectral resolution
The clear identification of the individual components of a spectrum is called
the spectral resolution. The best spectral resolution is obtained with no
truncation. This implies that the record length must be, at the least,
one complete cycle of a periodic signal and the whole nonzero part of an
aperiodic signal. With truncation, the resolution is affected in two ways.
Zero padding of a signal makes its spectrum denser, but it can not improve
the resolution.
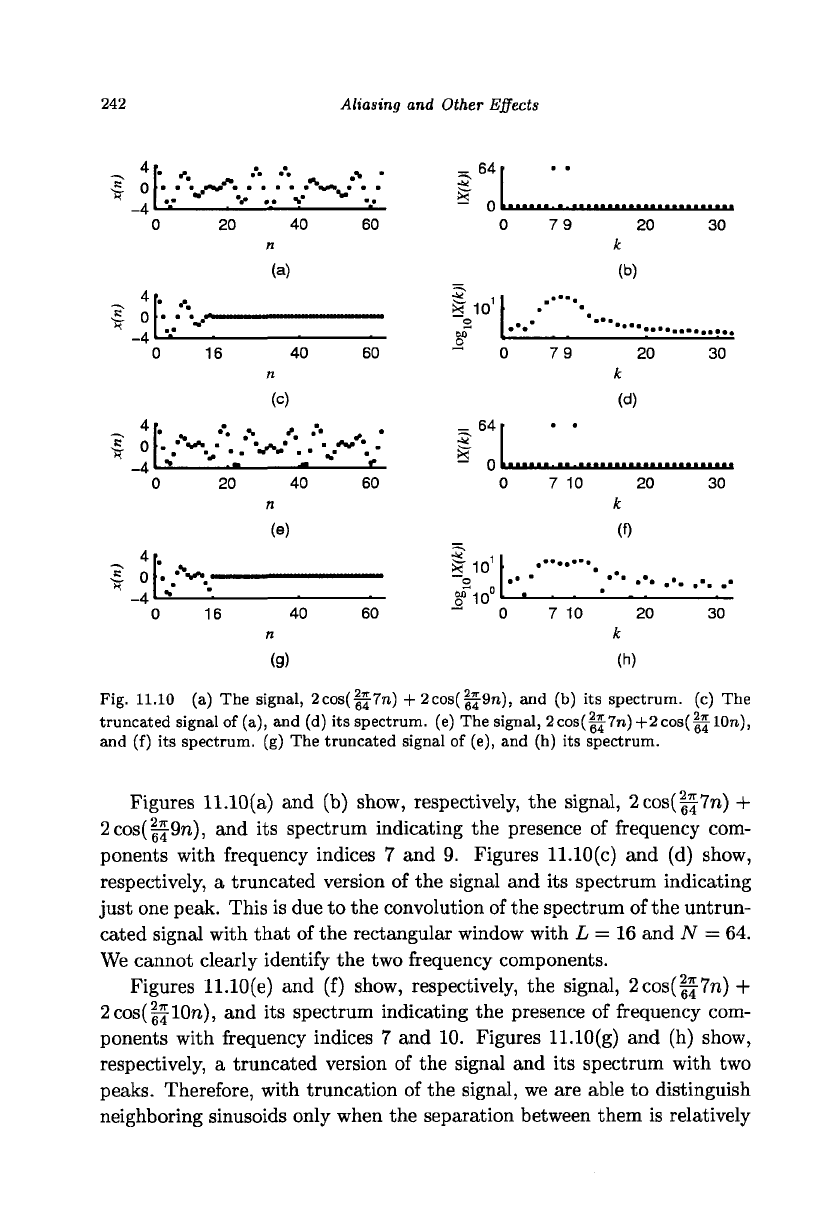
242
Aliasing and Other Effects
"fir
£
"><"
"?
X
X
;
rr
•
0 20
4
0
-4
• A
•-•
0 16
•'• •"• -. A •
• • • • <^*L* • •
40
n
(a)
40
n
(c)
0 20
4
0
f"
-\ -
.„
-. ^.——
0 16
11 in foi TI,O
40
n
(•>
40
n
(g)
60
60
60
60
~<v(
2
* 7n\ I
_ 64
3"
* 0
0
S? 10
1
o
9
.••'
- 0
_ 64
0
2 T
ST 10
o
oo i
n
0
.«
"
0
•Jmo^'On
79
• •
79
• •
7 10
•
7 10
^ CM ;+c
20
k
(b)
20
(d)
20
k
(f)
20
(h)
30
30
30
.". ••
30
f,-\ T\
truncated signal of (a), and (d) its spectrum, (e) The signal, 2cos(|j7n)+2cos(|jl0n),
and (f) its spectrum, (g) The truncated signal of (e), and (h) its spectrum.
Figures 11.10(a) and (b) show, respectively, the signal, 2cos(g|7n) +
2cos(|f9n), and its spectrum indicating the presence of frequency com-
ponents with frequency indices 7 and 9. Figures 11.10(c) and (d) show,
respectively, a truncated version of the signal and its spectrum indicating
just one peak. This is due to the convolution of the spectrum of the untrun-
cated signal with that of the rectangular window with L = 16 and N = 64.
We cannot clearly identify the two frequency components.
Figures 11.10(e) and (f) show, respectively, the signal, 2cos(|f-7n) +
2cos(|^10n), and its spectrum indicating the presence of frequency com-
ponents with frequency indices 7 and 10. Figures 11.10(g) and (h) show,
respectively, a truncated version of the signal and its spectrum with two
peaks.
Therefore, with truncation of the signal, we are able to distinguish
neighboring sinusoids only when the separation between them is relatively
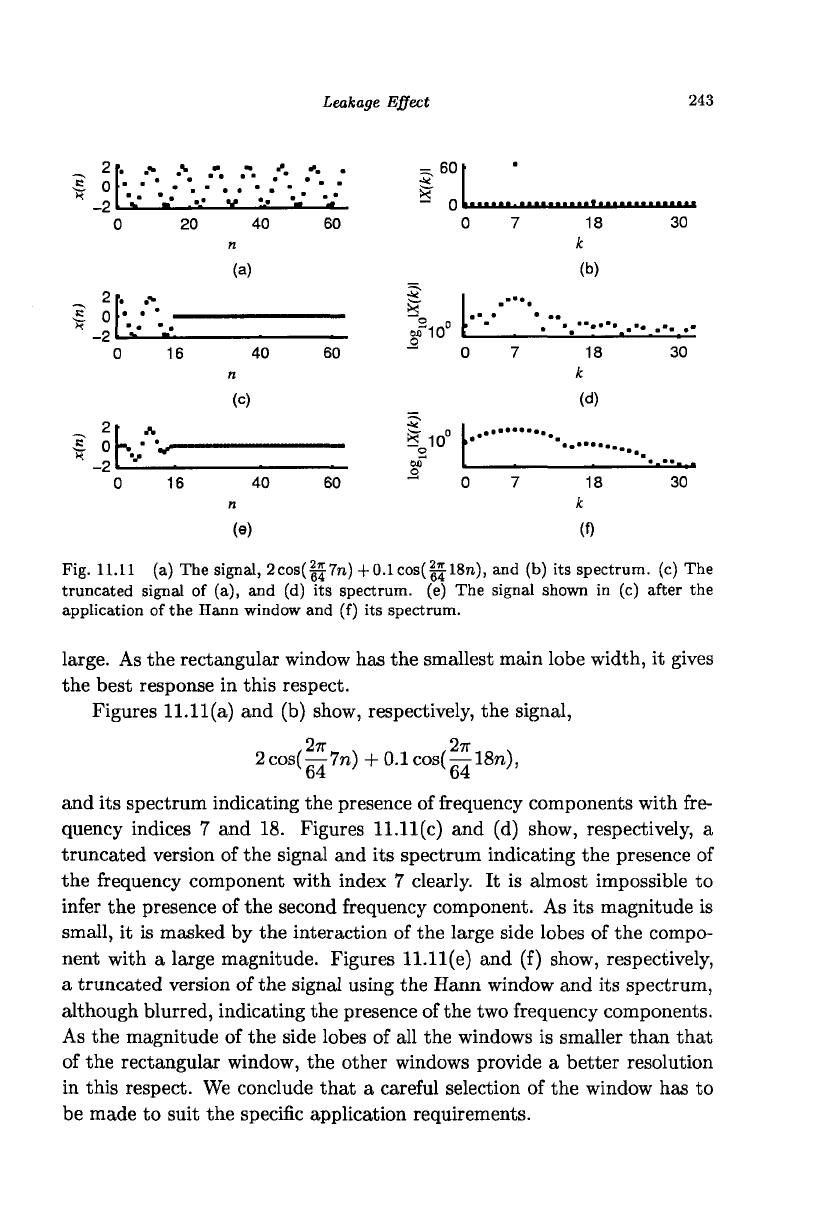
Leakage Effect
243
-
2
r« •"•
£ 0 • • '
_2L»—
16
2r A
°tv>:
16
20 40
n
(a)
40
(c)
40
60
60
60
60
5 I
t
2
10°
[
*10"
18
(b)
18
30
• •
0 7
• •."••••.-"• •"• ••
18 30
k
(d)
30
(e)
(0
Fig. 11.11 (a) The signal, 2cos(||7n) +0.1cos(|jl8n), and (b) its spectrum, (c) The
truncated signal of (a), and (d) its spectrum, (e) The signal shown in (c) after the
application of the Hann window and (f) its spectrum.
large. As the rectangular window has the smallest main lobe width, it gives
the best response in this respect.
Figures 11.11(a) and (b) show, respectively, the signal,
2 cos(-^7n) + 0.1 cos(-^18n),
64 64
and its spectrum indicating the presence of frequency components with fre-
quency indices 7 and 18. Figures 11.11(c) and (d) show, respectively, a
truncated version of the signal and its spectrum indicating the presence of
the frequency component with index 7 clearly. It is almost impossible to
infer the presence of the second frequency component. As its magnitude is
small, it is masked by the interaction of the large side lobes of the compo-
nent with a large magnitude. Figures 11.11(e) and (f) show, respectively,
a truncated version of the signal using the Hann window and its spectrum,
although blurred, indicating the presence of the two frequency components.
As the magnitude of the side lobes of all the windows is smaller than that
of the rectangular window, the other windows provide a better resolution
in this respect. We conclude that a careful selection of the window has to
be made to suit the specific application requirements.
