Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications
Подождите немного. Документ загружается.

214
Two-Dimensional Discrete Fourier Transform
C-vector R_vector R_stage 1 R-stage 2 Col_by_Col
a(0) =
z(0,0) ± x(l,0)
o(4) =
x(0,4) ± z(l,4)
o(2) =
x(0,2)±a;(l,2)
a(6)=o
x(0,6)±x(l,6)
o(l) =
z(0,l)±x(l,l)
a(5) =
x(0,5)±x(l,5)
o(3) =
z(0,3) ± x(l,3)
o(7)=o
x(0,7)±x(l,7)
f
A(0) =
U(0,0),I(0,4)
A(l) =
X(1,0),X(1,4)
r
A(2) =
11(0,1)^(0,5)
A(3) =
X(1,1),X(1,5)
Af4) =
X(0,2),X(0,6)
A(5) =
X(1,2),X(1,6)
Af6) =
X(0,3),X(0,7)
*±>A(7) =
6
X(l,3),X(l,7)
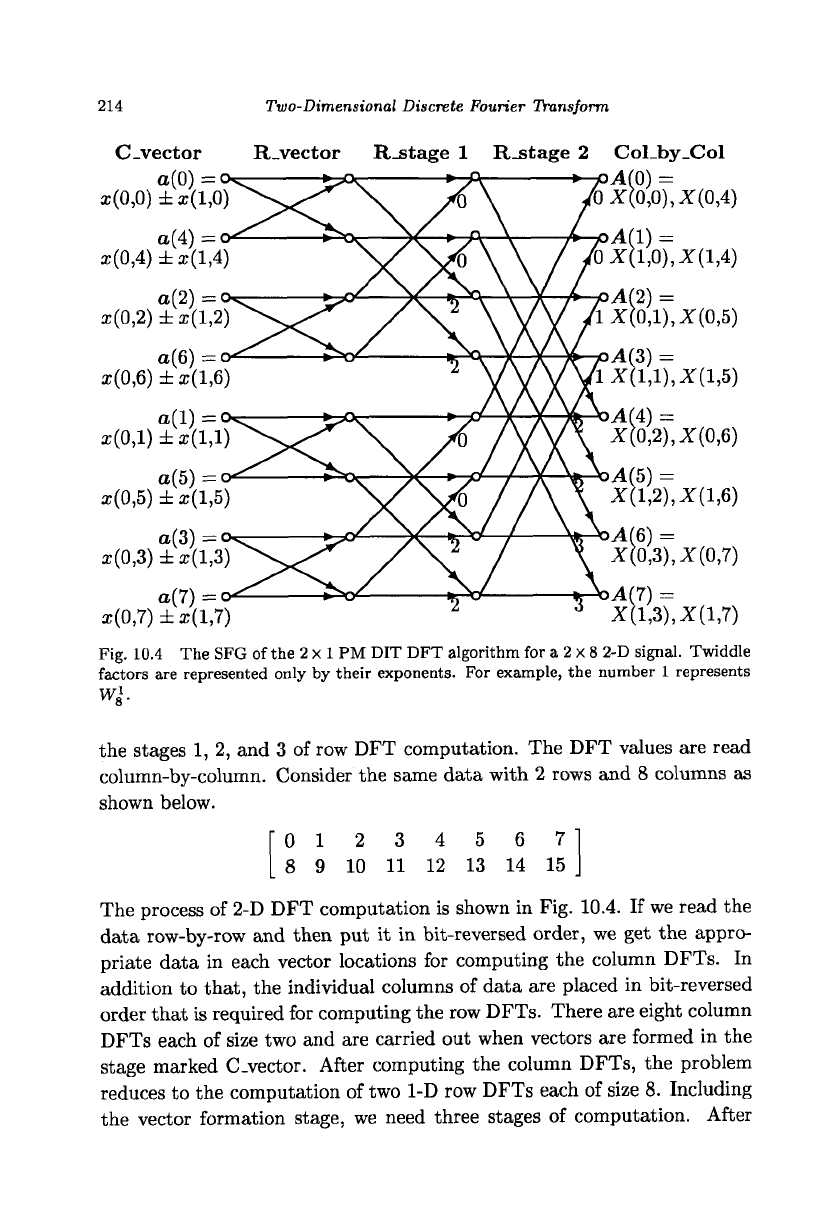
Fig. 10.4 The SFG of the 2 x 1 PM DIT DFT algorithm for a 2 x 8 2-D signal. Twiddle
factors are represented only by their exponents. For example, the number 1 represents
^s'-
the stages 1,2, and 3 of row DFT computation. The DFT values are read
column-by-column. Consider the same data with 2 rows and 8 columns as
shown below.
'01 2 3 4 5 6 7
8 9 10 11 12 13 14 15
The process of 2-D DFT computation is shown in Fig. 10.4. If we read the
data row-by-row and then put it in bit-reversed order, we get the appro-
priate data in each vector locations for computing the column DFTs. In
addition to that, the individual columns of data are placed in bit-reversed
order that is required for computing the row DFTs. There are eight column
DFTs each of size two and are carried out when vectors are formed in the
stage marked C.vector. After computing the column DFTs, the problem
reduces to the computation of two 1-D row DFTs each of size 8. Including
the vector formation stage, we need three stages of computation. After

The 2-D PM DFT Algorithms
215
computing the row vectors in the stage marked R_vector, the upper nodes
of the butterflies contain the vectors in the required order (0, 2, 1, 3) for
the computation of the first row DFT carried out in the next two stages.
The second row DFT is carried out using the vectors at the lower nodes
of the butterflies. It is clearly seen that each set of alternate butterflies
in the last two stages constitutes a row DFT and we get the 2-D DFT
column-by-column in natural order. Consider the same data with 4 rows
and 4 columns as shown below.
"0 1 2 3 "
4 5 6 7
8 9 10 11
. 12 13 14 15 .
The SFG, shown in Fig. 10.5, shows the computation of the 4 independent
column DFTs each of size 4 followed by the computation of the 4 indepen-
dent row DFTs each of size 4. While the butterflies of each of the column
DFTs appear together, every fourth butterfly in the last stage computes
each of the 4 independent row DFTs. Note that there are only four butter-
flies in a stage which means one butterfly to each row DFT. Consider the
same data with 8 rows and 2 columns as shown below.
0
2
4
6
8
10
12
14
I—>
3
5
7
9
11
13
15
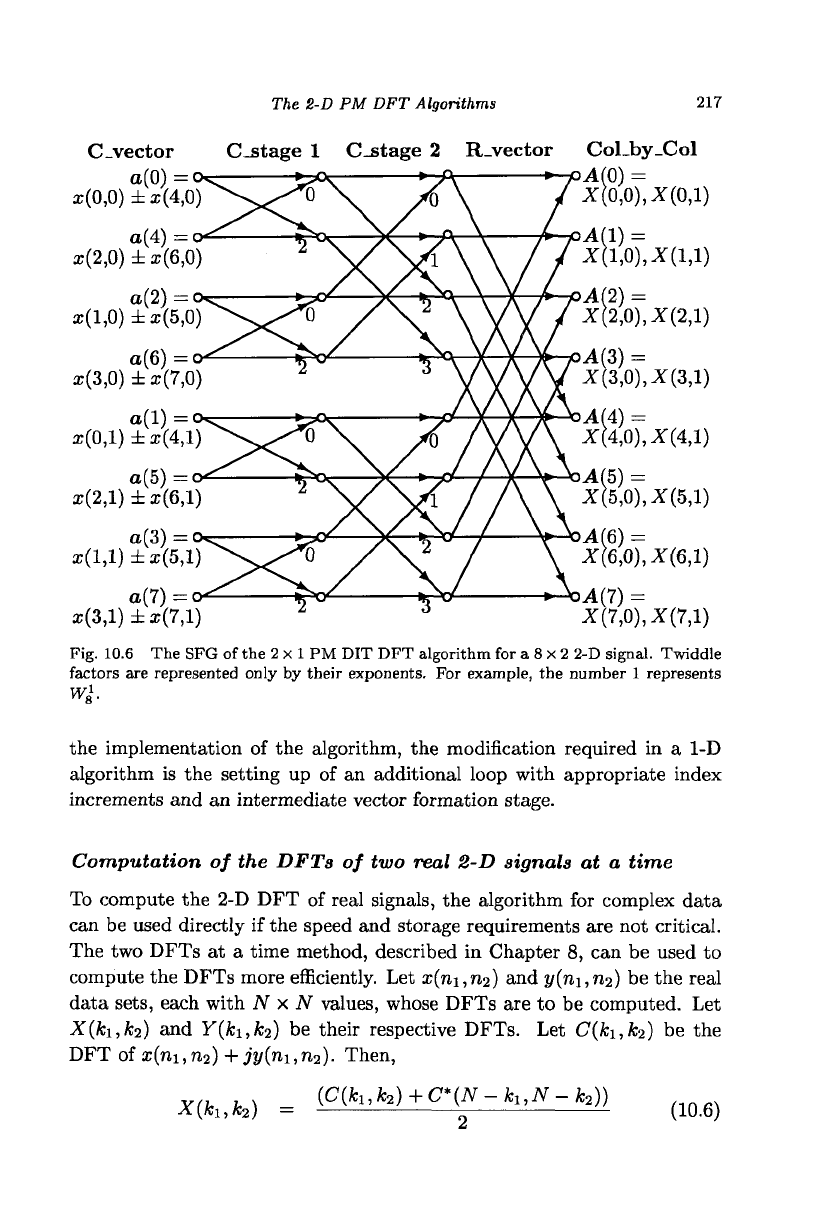
The SFG, shown in Fig. 10.6, shows the computation of the 2 independent
column DFTs each of size 8 followed by the computation of the 8 indepen-
dent row DFTs each of size 2. The last stage is the vector formation stage
for the row DFTs and no more stages are required since each row has only
two elements.
In summary, we read the data row-by-row (column-by-column), com-
pute the required number of column (row) DFTs, followed by the required
number of row (column) DFTs, and read the DFT values column-by-column
(row-by-row). The vectors for the individual column (row) DFTs are placed

216
Two-Dimensional Discrei le Fourier Transform
C-vector
o(0) =
a;(0,0)±x(2,0)
a(4) =
z(l,0) ± z(3,0)
o(2) =
ar(0,2) ± ar(2,2)
0(6) = »
x(l,2) ± ar(3,2)
«(!) =
z(0,l) ± z(2,l)
o(5) =
a;(l,l)±ar(3,l)
o(3) =
z(0,3) ± x(2,3)
o(7)=c
x(l,3)±x(3,3)
C-stage 1 R_vector Rjstage 1 Col_by_Col
r
A
W =
'0X(0,0),X(0,2)
A(l) =
X(1,0),X(1,2)
t)X(2,0),X(2,2)
Af3) =
X(3,0),X(3,2)
AU) =
X(0,1),X(0,3)
ii(5) =
X(1,1),X(1,3)
X(2,1),X(2,3)
1
Z(3,1),X(3,3)
Fig. 10.5 The SFG of the 2 x 1 PM DIT DFT algorithm for a 4 x 4 2-D signal. Twiddle
factors are represented only by their exponents. For example, the number 1 represents
consecutively in bit-reversed order whereas the vectors for the individual
row (column) DFTs are placed at intervals, the interval being the number
of rows (columns), in the bit-reversed order. The reader is urged to com-
pute the 2-D DFTs using the SFGs shown in Figs. 10.4, 10.5, and 10.6 and
verify that DFT values are the same as those obtained by direct computa-
tion. With the sizes of the row and column DFTs being powers of two, the
similarities and differences between 1-D and 2-D DFT computation are:
(i) the bit-reversal operation required is the same and independent data
swapping is eliminated in the first vector formation stage, (ii) the structure
of the SFGs is the same for the same number of data elements, and (iii)
the twiddle factors are different. One large 1-D DFT is computed in the
1-D case whereas a number of smaller 1-D DFTs are computed in the 2-D
case.
We can choose any algorithm for computing the 1-D DFTs required
in computing the 2-D DFT. With a good knowledge of 1-D algorithms,
it is simple to deduce the SFG for the computation of the 2-D DFT. In
The
2-D PM DFT Algorithms 217
C_vector Cstage 1 C_stage 2 R_vector Col_by_Col
o(0) = <*- ^- ^-Pr
+-pA(0)
=
x(0,0)±x(4,0)^y
<
^0 \ A\ / X(0,0),X(0,1)
a(4) =o^— -^ov \S > A \ M-pA{\) =
x(2,0)±x(6,0)
Z
y Vf \\ / / *(1,0),X(1,1)
a(2) = <*- £?cX N( ijNv \Y/ pA{2) =
x{lfi)±x{5,0)^^
>
^0 /\~ \ y y / X(2,0),X(2,1)
a(6) = 0^— ^cA 'T^\ A A )T y°
A
(
3
) =
x(3,0)±x(7,0)
Z 6
VYYV A
-
(3,0),A
-
(3,1)
a(l) = 0^- £*v >-*/ A A R vAU) =
x(0,l)±x(4,l)\
><
^
,
0 X *6 /yy\ X(4,0),X(4,1)
a(5) =0^— ^r
0
^ y<C
*
/> /AT "-^(5) =
x(2,l)±z(6,l)
2
V/ Vf //\\ A(5,0),^(5,l)
o(3) = o^- y/ >< V
0
^-/ V^o^(6) =
a;(l,l) ± x(5,l) ^^"*0 / \~ / \ X(6,0),X(6,1)
a(7) =0^— -5^°^ n^- »AM(7) =
z(3,l)±:r(7,l)
6
X(7,0),X(7,1)
Fig.
10.6 The SFG of the 2 x 1 PM DIT DFT algorithm for a 8 x 2 2-D signal. Twiddle
factors
are represented only by their exponents. For example, the number 1 represents
Wl.
the implementation of the algorithm, the modification required in a 1-D
algorithm is the setting up of an additional loop with appropriate index
increments and an intermediate vector formation stage.
Computation of the DFTs of two real 2-D signals at a time
To compute the 2-D DFT of real signals, the algorithm for complex data
can be used directly if the speed and storage requirements are not critical.
The two DFTs at a time method, described in Chapter 8, can be used to
compute the DFTs more efficiently. Let a:(ni,n
2
) and y(ni,n
2
) be the real
data sets, each with N x N values, whose DFTs are to be computed. Let
X(ki,k
2
) and Y(fci,fc
2
) be their respective DFTs. Let C(fci,fc
2
) be the
DFT of s(ni,n2)+jy(ni,n
2
). Then,
x{kuh) =
(C(k
uk2
)
+
C*(N-h,N-k
2
))
t
en
f
•a
a
9-
0
00
X
00
n
O
3
•o
HT
X
a
&
s>
%
'a*
to
*
I
a*
i
a-
Ul
h-' CO CO £».
H u oo en s u o
H P M H I h-* P-* p-
1
COUicn£*-CftCOUiOS
HOocDusbbi^
IDONOOHSOllD
H H M U
Ul
CO
00
p
co
-j
b
o
i
ui
co
CO
to
-48.
P-
O
b
o
to
p
CO
oo
o
b
CO
1
Its.
P-*
co
b
o
i
o
Ip.
co
~j
bo
00
CO
po
Cn
*>.
b
o
•
to
b
o
i
i h-
1
t-» W i I—
l
(—
l
00
oo
1
Ul
to
CO
t—*
b
00
p-
1
CO
p-
1
1
b
00
o
o
1
to
co
bo
o
UI
b
o
•
P-*
•
b
o
oo
P-*
to
i^
**
00
to
1
t—'
o
UI
1
P-*
p
Ul
o
o
1
to
to
CO
oo
o
b
o
i
P-*
o
CO
00
co
to
b
o
p-*
to
i
bo
t—»
t—'
b
00
•
P-*
po
P-*
co
to
p
b
00
o
o
i
b
CO
co
b
o
OS
It-
CD
•
UI
b
o
co
P-*
p
CD
to
1
to
to
*-
1
CO
OS
o
o
o
co
to
to
b
o
to
b
o
i
P-»
b
o
o
CO
CO
UI
bo
Ul
P-*
Oi
l(^
CD
b
Ul
1
to
t—'
o
o
1
P-*
oo
co
i-
1
b
o
p-
1
p
J-
1
p-
1
CO
b
o
o
co
1
bo
UI
•
P-»
U!
b
to
i
oo
co
CO
00
UI
O
o
1
P-*
P-*
UI
OS
p-
1
b
o
i
CO
UI
*>.
b
o
o
CO
1
to
CO
to
1
o
1
P-
1
to
1
p-»
to
co
o
o
to
co
b
i
CO
t—»
b
o
i
co
co
•
co
b
o
o
co
i
co
bo
m
co
b
to
•
p-
1
P-*
CO
CO
UI
lt^
o
o
to
to
00
1
to
b
o
1
P-*
co
-J
to
b
o
X)
% s?
2 c S*
** •a
•r"n h*
&!
p
<T
^ <o
cr er
c p .
B
s;
H
o rt- a
i Ǥ
cr HJ
O. oo
-. X
3 00
TO
"}5
-, O
>o
3
00C»UlCOOSCO---ItO
bo^-ai-'uih-'Cot-'to
OOCOUlOlUi^-UlOO
P-
1
tO I t-
1
h-
1
I I—
1
to-jpp<icoooto
bobsoHOsb
ooooootooooo
h->
M P P M ^
oooti^~qoococop
f-
i
p-*h-»uibbbb
Ml^CDOlOlSHO)
a
cr
cr
o
cr
cr •
I
5
" pa
o e.
1-S
The 2-D PM DFT Algorithms
219
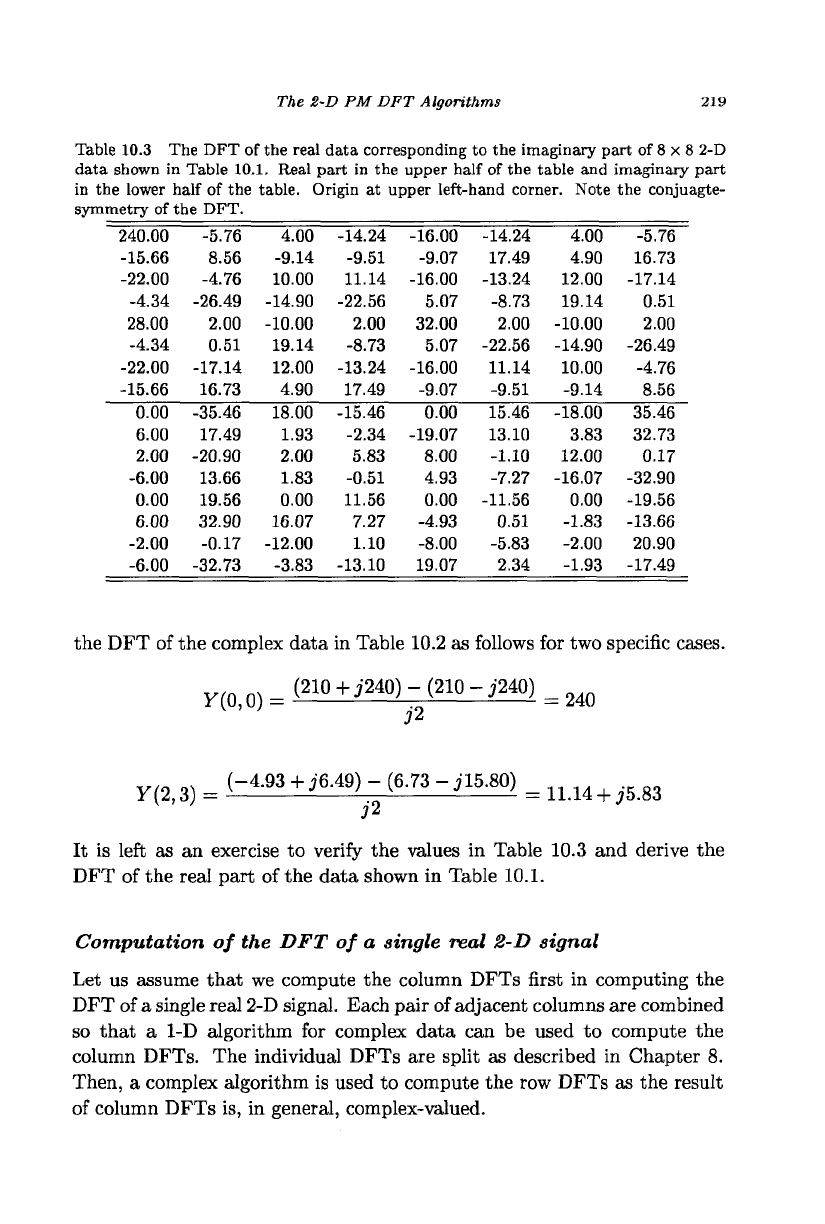
Table 10.3 The DFT of the real data corresponding to the imaginary part of 8 x 8 2-D
data shown in Table 10.1. Real part in the upper half of the table and imaginary part
in the lower half of the table. Origin at upper left-hand corner. Note the conjuagte-
symmetry of the DFT.
240.00
-15.66
-22.00
-4.34
28.00
-4.34
-22.00
-15.66
0.00
6.00
2.00
-6.00
0.00
6.00
-2.00
-6.00
-5.76
8.56
-4.76
-26.49
2.00
0.51
-17.14
16.73
-35.46
17.49
-20.90
13.66
19.56
32.90
-0.17
-32.73
4.00
-9.14
10.00
-14.90
-10.00
19.14
12.00
4.90
18.00
1.93
2.00
1.83
0.00
16.07
-12.00
-3.83
-14.24
-9.51
11.14
-22.56
2.00
-8.73
-13.24
17.49
-15.46
-2.34
5.83
-0.51
11.56
7.27
1.10
-13.10
-16.00
-9.07
-16.00
5.07
32.00
5.07
-16.00
-9.07
0.00
-19.07
8.00
4.93
0.00
-4.93
-8.00
19.07
-14.24
17.49
-13.24
-8.73
2.00
-22.56
11.14
-9.51
15.46
13.10
-1.10
-7.27
-11.56
0.51
-5.83
2.34
4.00
4.90
12.00
19.14
-10.00
-14.90
10.00
-9.14
-18.00
3.83
12.00
-16.07
0.00
-1.83
-2.00
-1.93
-5.76
16.73
-17.14
0.51
2.00
-26.49
-4.76
8.56
35.46
32.73
0.17
-32.90
-19.56
-13.66
20.90
-17.49
the DFT of the complex data in Table 10.2 as follows for two specific cases.
y(o,o)
=
(210+
^-
(210
-
J
'
240
^24o
j2
=
(-4.93
+J6.49)- (6.73 -J15.80)
= u
^
It is left as an exercise to verify the values in Table 10.3 and derive the
DFT of the real part of the data shown in Table 10.1.
Computation of the DFT of a single real 2-D signal
Let us assume that we compute the column DFTs first in computing the
DFT of a single real 2-D signal. Each pair of adjacent columns are combined
so that a 1-D algorithm for complex data can be used to compute the
column DFTs. The individual DFTs are split as described in Chapter 8.
Then, a complex algorithm is used to compute the row DFTs as the result
of column DFTs is, in general, complex-valued.

220
Two-Dimensional Discrete Fourier Transform
Computational complexity
The computational complexity of an TV x N 2-D DFT of complex data is
2N times that of the 1-D DFT algorithm used. The twiddle factors can be
generated once for all the rows and once for all the columns. This overhead
is,
therefore, becomes negligible. Consequently, no table is necessary for the
storage of twiddle factors. Further, the use of one-dimensional indexing and
the 1-D PM DFT algorithms makes the row-column approach of computing
the 2-D DFT practically very efficient. A single algorithm for complex data
is enough for both the DFT and IDFT computation. As in the case of the
1-D IDFT, for the 2-D IDFT computation using DFT, the data is to be
read and written with the imaginary and real parts interchanged.
10.6 Summary
• In this chapter, the theory, properties, and algorithms of the DFT of
2-D signals were presented. In the case of 2-D signals, Fourier anal-
ysis decomposes an arbitrary signal into a set of sinusoidal surfaces
of various frequencies, amplitudes, phases, and directions. Some
examples of simple 2-D signals and their DFTs were given.
• The 2-D DFT is a straightforward extension of the 1-D DFT. There-
fore,
practically efficient 2-D DFT algorithms are obtained by the
repeated use of the 1-D DFT algorithms. The computation of the
2-D DFT of real-valued signals is also similar to that of the 1-D
DFT.
References
(1) Gonzalez, R. C. and Woods, P. (1987) Digital Image Processing,
Addison Wesley, Reading, Mass.
(2) Jain, A. K. (1989) Fundamentals of Digital Image Processing, Prentice-
Hall, New Jersey.
(3) Sundararajan, D., Ahmad, M. 0. and Swamy, M. N. S. (1994)
"Computational Structures for Fast Fourier Transform Analyzers",
U.S. Patent, No. 5,371,696.

Exercises
221
Exercises
10.1 Verify that Eqs. (10.1) and (10.2) form a transform pair.
10.2 Prove Eq. (10.3) from Eq. (10.2).
10.3 Describe the sinusoidal surfaces shown in Figs. 10.1(h), (j), (n), (r),
and (v).
10.4 Find the DFT of the N x N 2-D dc signal, x(n
u
n
2
) = -3, from
definition.
10.5 Find the DFT of N x N delayed impulse signal, S(ni - l,n
2
- m),
from definition.
10.6 From definition, derive the DFT of a;(ni,n
2
) = e^'
m+mn2)
,ni,n
2
=
0,1,...,
N
—
1, where I and m are positive integers.
10.7 Compute the 2-D DFT of
(a) x(m,n
2
) = 2e-'w(4m+3n2)
) 0
< m < 64, 0 < n
2
< 64.
(b) x(ni,n
2
) = 3e^("
1+
"
2
), 0 < n
x
< 32, 0 < n
2
< 32.
(c) x{m,n
2
) = 4e^'f
(
3
"
2
),
0 < ni < 16, 0 < n
2
< 16.
*(d) x(n
u
n
2
) = -5e-^f
2ni+
e), 0 < m < 16, 0 < n
2
< 16.
(e) x(rn,n
2
) = 2sin(ff(4m +3n
2
) + f), 0 < m < 16, 0 < n
2
< 16.
*(f) x(n
u
n
2
) = 2sin(ff (4m +3n
2
) + f), 0 < ni < 32, 0 < n
2
< 32.
(g) x(n
u
n
2
) = 5cos(f|(2ni +5n
2
) - |), 0 < n
x
< 32, 0 < n
2
< 32.
(h) x(m,n
2
) = sin(^3ni), 0 < n
x
< 16, 0 < n
2
< 16.
(i) x(m,n
2
)
—
cos(fni), 0 < n\ < 16, 0 < n
2
< 16.
(j) x(ni,n
2
) = cos(7rn
2
), 0 < n\ < 16, 0 < n
2
< 16.
(k) x(ra,n
2
) = 4, 0 < ri! < 4, 0 < n
2
< 4.
(1) a;(0,0) = 3 and x(ni,n
2
) = 0 otherwise, 0 < n\ < 4, 0 < n
2
< 4.
10.8 Compute the 2-D IDFT of
(a) X{ki,h») = 7, 0 < h < 5, 0 < fc
2
< 5.
(b) X(0,0) = 8 and X{k
u
k
2
) = 0 otherwise, 0 < h < 3, 0 < k
2
< 3.
(c) X(2,1) = 26 and X(k!,k
2
) = 0 otherwise, 0 < fci < 16, 0 < k
2
< 16.
(d) X(3,0) = -46 and X(k
lt
k
2
) = 0 otherwise, 0 < A;i < 16, 0 < k
2
< 16.
(e) X(13,15) = 23(^ - j^~) and X(k
u
k
2
) = 0 otherwise, 0 < h <
16,
0 < k
2
< 16.
*(f) X(2,3) = (i +j&), X(14,13) = (| - j&), and X{k
u
k
2
) = 0
otherwise, 0 < ki < 16, 0 < k
2
< 16.

222
Two-Dimensional Discrete Fourier Transform
(g) X(l,5) = (-^
-jj-),
X(15,ll) = (-^ +j±), and X(k
u
k
2
) = 0
otherwise, 0 < ki < 16, 0 < k
2
< 16.
(h) X(5,4) = 4, X(ll,12) = 4, and X(jfci,*
2
) = 0 otherwise, 0 < fei <
16,
0 < k
2
< 16.
(i) X(10,8) = 16, X(22,24) = 16, and X(k
u
k
2
) = 0 otherwise, 0 < h <
32,
0 < k
2
< 32.
(j) X(2,3) = -j8, AT(14,13) = j&, and X(h,k
2
) = 0 otherwise, 0 < h <
16,
0 < k
2
< 16.
(k) X(2,6) = -3, X(14,10) = -3, and X(k
u
k
2
) = 0 otherwise, 0 < h <
16,
0 < k
2
< 16.
*(1) X(2,2) = -j5 and X(k
u
k
2
) = 0 otherwise, 0 < fci < 16, 0 < k
2
< 16.
10.9 Compute the DFT of the following image using the row-column method.
Then, compute the IDFT of the transform using the DFT and verify that
the original image is obtained.
ni
n
2
2
1
4
2
1
0
1
0
3
1
0
1
3
2
1
2
10.10 Compute the DFT of the first two images. Using the resulting trans-
forms,
deduce the transform of the third image by applying the linearity
theorem.
x
—
-1 -3
-4 -2
2 3
1 4
z =
-1-J2 -3-J3
-4-jl -2-J4
*10.11 For the image of Exercise 10.9, deduce the transform values X(7,21),
X(—4,
—3),
and X(l,
—3),
using the periodicity property.
10.12 For the image of Exercise 10.9, deduce the image values x(7,42),
x{—9,
—4),
and x(2,
—7),
using the periodicity property.
10.13 For the image of Exercise 10.9, deduce the spectrum of x(ni -
2,
n
2
-!-
3),
using the shift property.
10.14 For the image of Exercise 10.9, deduce the spectrum if the image is
multiplied by 2e~
j2
^
(
-
3ni
~
2n
^, using the shift property.

Exercises
223
10.15 For the image of Exercise 10.9, deduce the spectrum of x (ni,n2)
*10.16 Underline the upper half of the nonredundant transform values of
the image of Exercise 10.9.
10.17 Find the DFT of x(m) = |cos(^ni), 0 < ni < 4 and x(n
2
) =
isin^r^),
0 < n
2
< 4. Then, deduce the DFT of ar(ni,n
2
) = x(ni)x(n
2
)
using the separability theorem.
*10.18 For the image of Exercise 10.9, verify the Parseval's theorem.
Programming Exercises
10.1 Write a program to directly implement the 2-D DFT using the row-
column method.
10.2 Write a program to directly implement the 2-D ID FT using the row-
column method.
10.3 Write a program for the computation of the 2-D DFT of a complex-
valued image using the 2 x 1 PM DIT DFT algorithm.
