Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления

Подождите немного. Документ загружается.

211

печения энергетического баланса гидравлических энергий: разность

суммы гидравлических энергий, в единицу времени поступающих в

активные узлы извне, и суммы гидравлических энергий, в единицу

времени исходящих из активных узлов в рассматриваемой гидросис-

теме, должна равняться сумме гидравлических мощностей N

звеньев

гидросистемы N

()

∑∑

Δ−=Δ

iiiiii

qzqqfqp

В развернутом виде система (4.4) имеет вид

Данная система уравнений неоднородна и имеет сходство с мето-

дом «поконтурной увязки расходов», однако, в системе (4.4) нет

структурно-замкнутых контуров, и узлы гидросистемы входят в сис-

тему уравнений по-разному: имеется разделение на активные и тран-

зитивные узлы.

Описанная система уравнений является системой нелинейных ал-

гебраи

ческих уравнений, которая может быть решена численным ме-

тодом Ньютона, модифицированным автором, при начальных прибли-

жениях q

=0. Ограничением на вид функций гидравлических характе-

ристик является только определимость функций на всей числовой

плоскости.

Факторами данной модели являются давления во всех активных уз-

лах и заданные зависимости

)(qf

для всех звеньев модели гидросис-

темы.

Еще одной особенностью данной системы уравнений является ми-

нимальное количество вхождений в уравнения (4.3) нелинейных замы-

… a

…

… a

… b

…

… b

…

… b

…

′

…

′

…

′

= 0

…

212

кающих отношений

)(

qf , что обеспечивает нивелирование основ-

ных проблем при решении этой системы уравнений. Это достигается, с

одной стороны, самой постановкой задачи (выбором факторов модели

и представлением структуры), а с другой стороны, тенденциозным

выбором системы путей: по принципу выбора кратчайших путей, ох-

ватывающих все звенья. Как выявлено, выбор системы кратчайших

путей в матрице

B часто позволяет рассчитывать гидросистемы, даже

если они (пути) будут линейно-зависимыми.

В известных ранее моделях таких ограничений больше, что связано

с выбором в качестве дополнительных факторов модели фиксирован-

ных оттоков/притоков текучей среды в определенных узлах, что, по

мнению автора, является не адекватным для задач имитации гидросис-

тем с достаточной точностью.

динственным недостатком исходной системы уравнений (4.4) яв-

ляется необходимость поиска системы из c линейно-независимых пу-

тей, что для структурно-сложных систем может оказаться невыполни-

мо.

Система уравнений (4.4) и способ ее решения автором названы со-

гласно принятой в теории гидравлических цепей традиции методом

«путевой увязки».

Как показал опыт автора данной работы, с

истема уравнений (4.4)

позволяет решать потокораспределение произвольных гидросистем с

наибольшей вычислительной скоростью и точностью. Такие результа-

ты были получены благодаря не только особенностям системы (4.4),

но и предложенному модифицированному методу Ньютона для реше-

ния данной системы уравнений, рассмотренному в разделе 4.4.

Рассмотрим пример формирования системы уравнений, соответст-

вующей методу «путевой увязки». Приведем пример полной м

атрицы

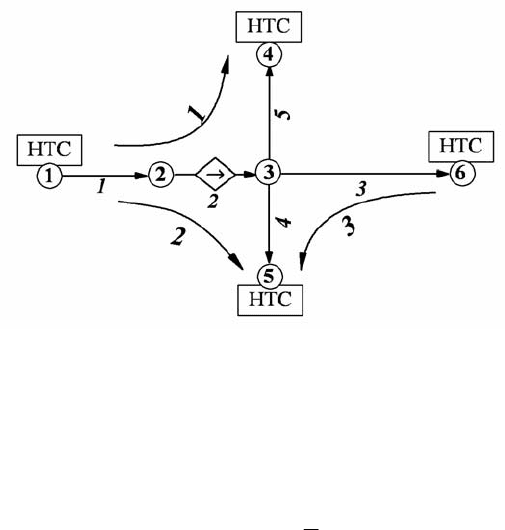
А для схемы, состоящей из 5 звеньев и 6 узлов (см. рис. 4.5).

Матрица

А будет иметь следующий вид:

–1 0 0 0 0

1 –1 0 0 0

0 1 –1 –1 –1

0 0 0 0 1

0 0 0 1 0

0 0 1 0 0

1 2 3 4 5

213

В каждом столбце матрицы только два ненулевых элемента: 1 и –1,

поэтому сумма всех ее строк дает нулевую строку, что означает их

линейную зависимость.

Матрица соединений выполняет ряд взаимосвязанных между собой

функций. Во-первых, как уже отмечалось, она представляет порядок

соединения объектов рассматриваемой ТГС, т.е. ее структурную схе-

му. Можно считать структуру ТГ

С заданной, если известна ее полная

матрица соединений и наоборот. Таким образом, использование этой

матрицы в том или ином математическом описании и в его алгебраи-

ческом преобразовании автоматически учитывает конкретные особен-

ности структуры рассматриваемой ТГС.

Во-вторых, она позволяет дать алгебраическое описание матери-

ального баланса сразу во всех узлах, т.е. дл

я структурной схемы в це-

лом. Это следует из того, что каждое из уравнений материального ба-

ланса для любого из t транзитивных узлов можно представить в виде

скалярного произведения строки матрицы

А, соответствующей этому

узлу, на один и тот же вектор-столбец

расходов во всех звеньях.

Поясним вышеизложенное на примере транзитивного узла 3 из схемы,

представленной на рис. 4.5.

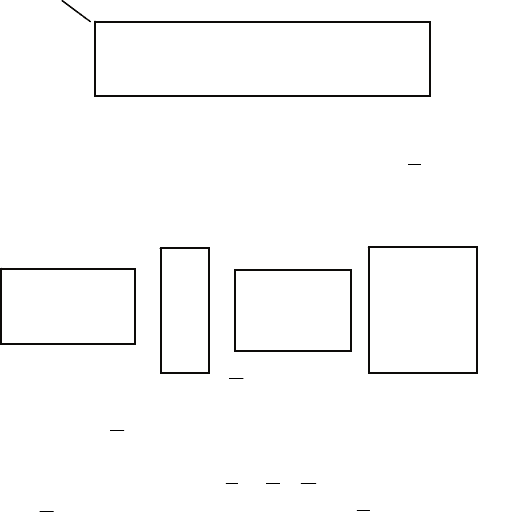
Рис. 4.5. Структурная схема ТГС с четырьмя накопителями текучей среды

и одним АСГ. Цифрами указаны номера звеньев, узлов и путей, а стрел-

ками – ориентация звеньев и направление обхода путей

214

Для узла 3 имеем:

что после выполнения скалярного произведения дает уравнение мате-

риального баланса q

– q

–q

= 0. Для всех узлов (исключая актив-

ные) рассматриваемой модели материальные балансы могут быть

представлены в виде произведения выделенных строк матрицы А на

вектор

× =

или кратко

QА

=0,

причем при построении искомой системы уравнений для рассматри-

ваемого примера из (4.5) следует исключить (т.е. принять нулевыми)

строки 1, 4, 5 и 6, соответствующие активным узлам (см. рис. 4.5). В

дальнейшем, под произведением

QА

следует понимать матрицу А с

нулевыми или отсутствующими строками для активных узлов.

С помощью полной матрицы

А можно в общем виде записать связь

между давлениями p

во всех транзитивных узлах и их перепадами Δp

на концах звеньев. Действительно, i-й столбец –

этой матрицы со-

держит информацию (в виде двух чисел 1 и –1 на соответствующих

местах – строках j

и j

) не только о концевых узлах данного звена

i=[j

, j

], но и его ориентации, поэтому

,PAppp

ijji

ieib

⋅−=−=Δ

где PA

⋅ – скалярное произведение столбца i транспонированной

матрицы соединений –

, записанного как вектор-строка, на вектор-

столбец

. Знак «–» справа необходим для устранения разницы меж-

= 0,

0 1 –1 –1 –1

–1 0 0 0 0

1 –1 0 0 0

0 1 –1 –1 –1

0 0 0 0 1

0 0 0 1 0

0 0 1 0 0

(4.5)

(4.6)

215

ду условиями построения матрицы

А, замыкающими отношениями

()

qf и вектором гидростатических перепадов –

, так как послед-

ние строятся исходя из разности давления/уровня между входом и вы-

ходом из звена, а в матрице соединений элемент, соответствующий

узлу начала звена, имеет значение –1.

По отношению ко всем звеньям модели выражение (4.6) даст

PAY

−=

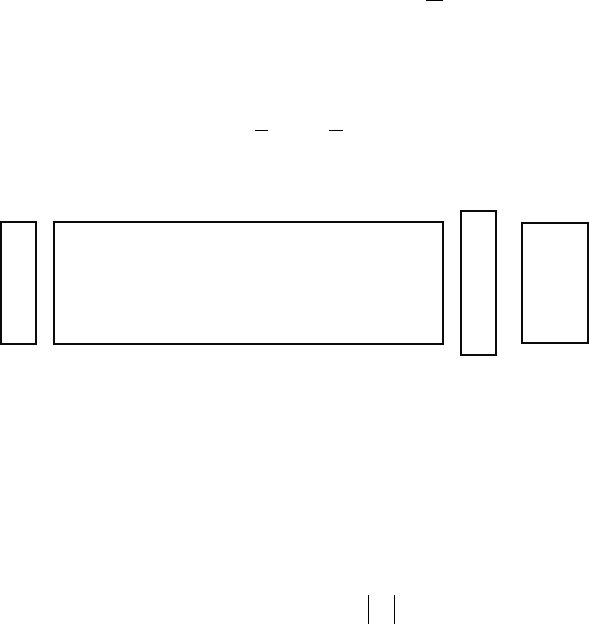
Для рассматриваемой системы (4.6) это будет выглядеть следую-

щим образом:

Матрица соединений, также называемая матрицей инциденций

вершин и дуг ориентированного графа, обладает свойством унимоду-

лярности [64], заключающимся в том, что определитель любой ее

квадратной подматрицы равен 0, +1 или –1.

Другой основной матрицей модели является матрица

В путей, ко-

торая фиксирует выбранную в модели систему путей. Основными тре-

бованиями к формированию данной матрицы являются:

1. Выбранной системой (множеством) путей должны быть покрыты

все звенья системы, т.е. сумма модулей элементов матрицы

B в каж-

дом столбце i не должна равняться нулю

≠

∑

b .

2. Система путей должна включать c линейно-независимых путей,

т.е. в матрице

B в каждой строке r должен присутствовать хотя бы

один ненулевой элемент b

(r, x)

, которого нет в остальных строках на

пересечении со столбцом x.

3. При соблюдении условий 1 и 2 желательно выбирать наикрат-

чайшие пути.

Для нашего примера гидросистемы (рис. 4.5), в ней просматрива-

ются три пути (они пронумерованы цифрами с круговыми стрелками,

показывающими заданные направления их обхода). Как мы услови-

–1 1 0 0 0 0

0 –1 1 0 0 0

0 0 –1 0 0 1

0 0 –1 0 1 0

0 0 –1 1 0 0

– p

–

– p

–

(4.7)

216

лись ранее, направления обхода путей задаются посредством указания

номеров активных узлов: узлов начала и конца пути.

Для нашего случая соответствующая матрица

B имеет вид:

Уравнения второй части системы (4.4) для отдельно взятого пути

могут быть записаны как скалярное произведение вектора-строки мат-

рицы

B, отвечающей этому пути, и вектора-столбца

. Для всех пу-

тей одновременно эти уравнения представляются уже в матричной

форме, в следующем виде:

где справа первым стоит вектор

, составленный из разностей давле-

ний P

–P

между активными узлами, соответствующими пути r, а вто-

рым стоит вектор

гидростатических перепадов между активными

узлами. Или кратко это будет выглядеть так:

B·

UE +

Вектор

определяется аналогично вектору

: u

равен сумме гид-

ростатических перепадов звеньев, входящих в соответствующий путь r

со знаком «–», или просто разности абсолютных отметок активных

узлов, образующих этот путь.

Теперь перейдем к рассмотрению известных в алгебре элементар-

ных преобразований матриц, которые имеют практическое значение

при построении и преобразовании расчетных схем моделей ГС и моде-

лей электрических систем.

1. Перест

ановка (транспозиция) любых двух строк равносильна из-

менению нумерации узлов (для матрицы

А) или путей (для матрицы

В). Транспозиция столбцов изменяет нумерацию звеньев. Эти опера-

ции позволяют упорядочить (сгруппировать) расположение нулевых

1 2 3 4 5

1 1 0 0 1

1 1 0 1 0

–1 1

∑

∈

Δ=

11 i

∑

∈

Δ=

22 i

∑

∈

Δ=

33 i

1 1 0 0 1

1 1 0 1 0

0 0 –1 1 0

–P

= +

(4.8)

217

элементов в матрицах и приводить их (если возможно) к тому или

иному (например, диагональному) виду.

2. Умножение столбца i на –1 изменяет ориентацию звена i на про-

тивоположную. Для изменения направлений обхода пути r следует

умножить на –1 строку r матрицы

В.

3. Сложение (вычитание) строк для матрицы

А приводит к новой

линейной комбинации узлов, а для

В – к новой системе путей. При-

бавим, к примеру, в матрице

А рассматриваемой гидросистемы первую

строку ко второй. Получим новую матрицу

′

и соответствующую

схему модели (см. рис. 4.6 – а).

′

=1+

Таким образом, для матрицы

А происходит объединение узлов 1 и

2 в один результирующий узел 1+2 в

′

Теперь вычтем из второй строки матрицы

В третью и получим мат-

рицу

′

, соответствующую системе путей, изображенной на

рис. 4.6 – б.

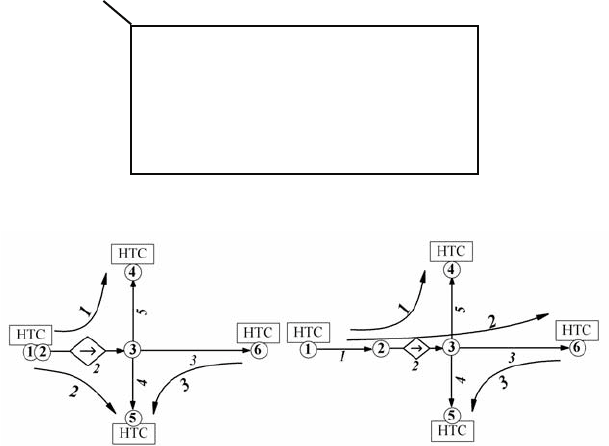
а) б)

Рис. 4.6. Преобразованная схема МТГС: а – в результате сложения строк

в матрице

А; б – в результате сложения в матрице В

–1 0 0 0 0

0 –1 0 0 0

0 1 –1 –1 –1

0 0 0 0 1

0 0 0 1 0

0 0 1 0 0

1 2 3 4 5

218

′

=2 – . .

Очевидно, что число таких линейных комбинаций векторов-строк

матрицы

В и связанных с ними вариантов систем путей будет очень

большим даже для сравнительно простых гидросистем. Вместе с тем

среди них можно выделить те, которые принципиально отличаются от

всех прочих и являются предпочтительными.

Эффективность описываемого метода «путевой увязки» в основном

зависит от матрицы

B. Естественно, выбор системы путей вручную для

произвольных гидросистем невозможен. Поэтому для данного метода

предлагается алгоритм поиска наиболее эффективной матрицы

B (см.

раздел 5.6)

Между матрицами и векторами МГС существуют соотношения, ко-

торые являются математическим отражением сетевого характера изу-

чаемых ТГС и служат инструментом для преобразования к путевым и

узловым величинам. Прежде всего, выясним связь между матрицами

соединений и путей, т.е. А и В.

Рассмотрим однородную систему уравнений материального балан-

са:

⋅

Q=0

и покажем, что любая строка матрицы

B является ее решением. Дейст-

вительно, пусть a

=(a

, … , a

) – j-я строка A (j=1 , … , m–1), а b

=(b

… , b

) – r-я строка B (r = 1 , … , c), где элементы a

и b

(i=1 , … , n)

принимают значения 0, 1 и –1 (как это описано выше).

В случае, когда путь r не проходит через узел j, ненулевые элемен-

ты a

и b

имеют обязательно различные номера i, и потому скалярное

произведение a

=0. Если же простой путь r проходит через узел j, то

ему могут принадлежать лишь два звена: i

и i

, инцидентные данному

узлу, и только для них одновременно не равны нулю соответствующие

элементы a

и b

, так что скалярное произведение фактически будет

сводиться к сумме двух слагаемых:

2211

rijirijij

babaa +=

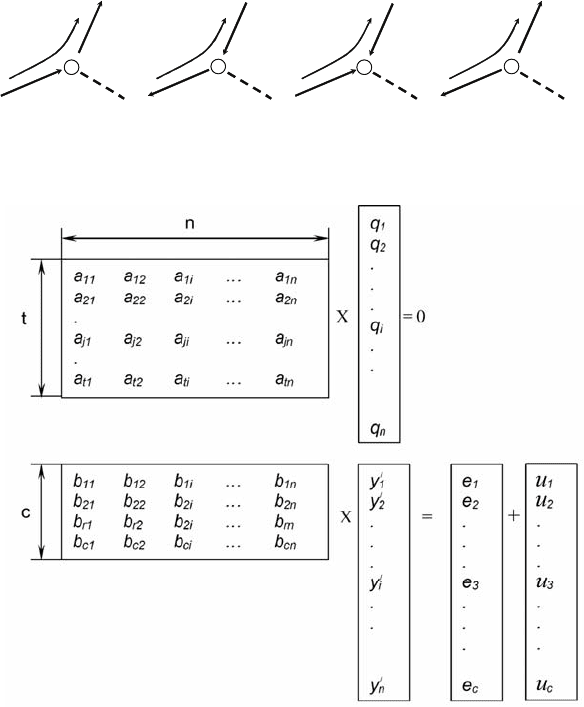
Как видно из рис. 4.7, в любом случае прохождения пути через узел

j произведения в правой части (4.10) обязательно имеют различные

1 2 3 4 5

1 1 0 0 1

1 1 1 0 0

–

(4.9)

(4.10)

219

знаки, так что их сумма равна нулю и потому всегда a

=0.

Так как это справедливо для любых j и r, то, во-первых,

⋅

=0; r = 1, … , c,

т.е. любая строка матрицы

B (берущаяся здесь как вектор-столбец)

удовлетворяет системе (4.9), во-вторых, это может быть записано сразу

для всех строк, что приведет к искомому произведению матриц

⋅

= 0

Отразим структуру и размерности системы (4.4) схематично для

обобщения изложенного материала.

а)

б) в)

г)

Рис. 4.7. Различные сл

чаи п

охождения п

ти

че

ез

зел

(4.11)

(4.12)

220

Эта система состоит из n уравнений относительно неизвестного

вектора

Q, причем, первая подсистема представлена t уравнениями

вида (4.2), отражающими материальный баланс в t транзитивных уз-

лах, а вторая подсистема представлена c уравнениями вида (4.3), отра-

жающими выражение второго закона Кирхгофа для разомкнутых сис-

тем.

С целью более удобной и компактной записи отдельных подсистем

уравнений, а также операций над ними (различных подстановок, взя-

тия п

роизводных и т.д.) введем следующие обозначения:

() ()

()

ueqfb

ueqfQv

UEYBQv

qaqQsQAQs

iir

,...,2,1

)(

,...,2,1

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

−−

=−−=

=−−

′

⎭

⎬

⎫

⎩

⎨

⎧

====

∑

где

∑∑

означают суммирование по всем звеньям i, инцидент-

ным соответственно транзитивному узлу j или пути r;

– стро-

ки j и r соответственно матриц

А и В.

В результате система (4.4) может быть записана также следующим

образом:

Q)=0, v(Q)=0.

Таким образом, имеет систему нелинейных уравнений относитель-

но неизвестных установившихся расходов –

Корректность постановки задачи моделирования ТГС. Решение

этого вопроса связано, прежде всего, с пониманием физического

смысла задачи и, в конечном счете, зависит от правильности соотно-

шения заданных и искомых величин, от соразмерности степени дета-

лизации и агрегирования схемы к качеству и количеству имеющихся

исходных данных и от разброса в их величинах.

Сис

тема уравнений, представленная выше, рассчитана на один

важный, но частный случай. Во-первых, когда задаются давления во

всех накопителях текучей среды. В случае, когда задаваемым НТС

является река, озеро или какая-либо другая емкость, величину давле-

(4.13)

(4.14)

(4.15)