Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления

Подождите немного. Документ загружается.

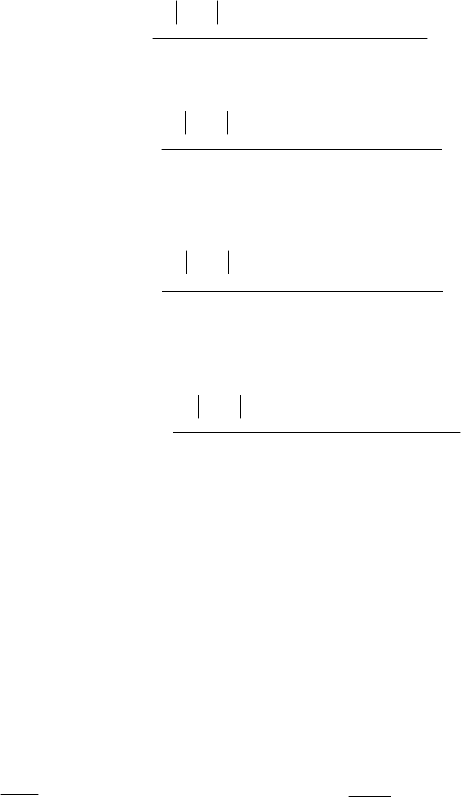
241

[]

⎪

⎩

⎪

⎨

⎧

++⋅

∑

∈

∈∈∈

∈

∈∈∈

∈

∈∈∈

∈

∈∈∈

kkikikki

mknmkmkm

kkikikki

jknjkjkj

kkikikki

knkk

kkikikki

knkk

x)T,M(TM

)T,...,T,T(

x)T,M(TM

)T,...,T,T(

x)T,M(TM

)T,...,T,T(

x)T,M(TM

)T,...,T,T(

εθ

222212

112111

относительно неизвестных температур

в узлах.

После определения температур во всех узлах можно рассчитать

окончательное термораспределение по звеньям посредством решения

(4.33) для каждого участка.

На рис. 4.13 показаны примеры расчетного распределения темпера-

туры потока, установившегося в трубопроводе с внутренним диамет-

ром 50 мм, длиной 1000 м и абсолютной шероховатостью 0.5 мм при

установившемся течении сжимаемой воды с массовым расходом

=1000 т/сут, давлением на входе

=20 МПа и температурой на

входе

=40

C. Распределение температуры окружающей среды

равномерно

) = const = 4

C. Коэффициент теплопередачи

γ=10.51

Км

Вт

. Удельная теплоемкость

4200

Ккг

Дж

⋅

(4.43)

242

38.4

38.6

38.8

39.2

39.4

39.6

39.8

40.2

0 200 400 600 800 1000 1200

Длина, м

Температура, `C

а)

39.8

40.2

40.4

40.6

40.8

41.2

41.4

41.6

41.8

0 200 400 600 800 1000 1200

Длина, м

Температура, `C

б)

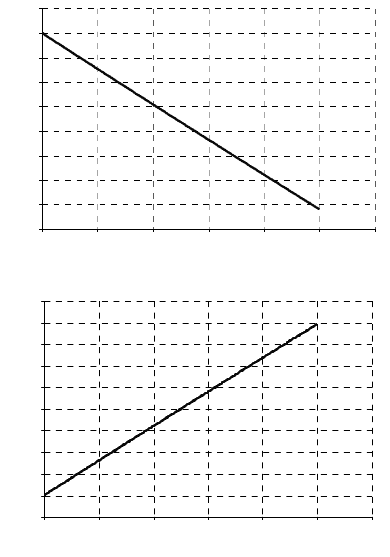
Рис. 4.13. Пример распределения температуры по длине трубопровода: а – без

учета гидротермического перехода;

б – с учетом гидротермического перехода

Как видно из графика на рис. 4.13 – а, построенного без учета пере-

хода гидравлической энергии потока в тепловую, распределение тем-

пературы по длине звена соответствует снижению температуры потока

вследствие теплопередачи во внешнюю среду. Однако, если учитывать

данный факт, то распределение температуры существенно меняется

(см. рис. 4.13 –

б): температура по длине растет.

С целью выявления влияния теплопередачи во внешнюю среду рас-

смотрим распределение температуры того же звена при

=10 т/сут с

учетом гидротермического перехода (ГТ) (см. рис. 4.14).

243

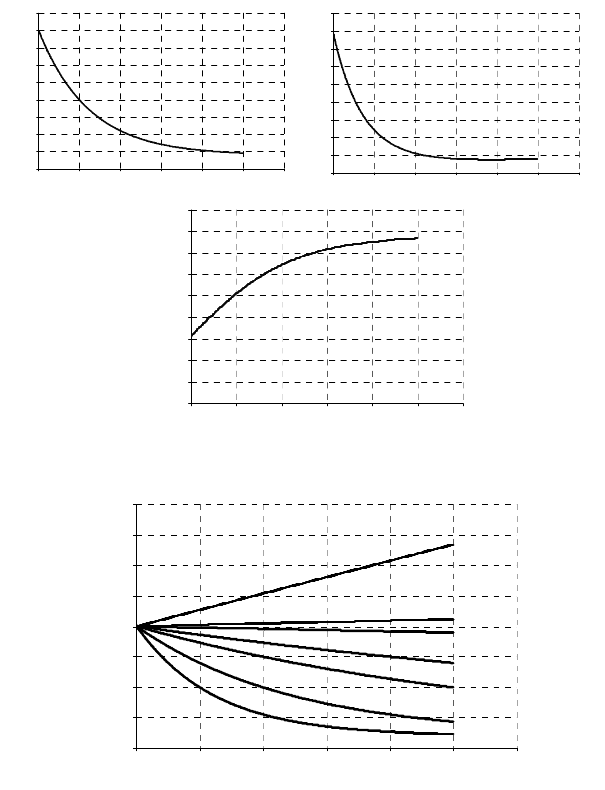
Рис. 4.14. Пример распределения температуры, объемного расхо-

да и кинематической вязкости по длине трубопровода

Как видно из графиков падение температуры по длине звена имеет

нелинейный характер вследствие снижения теплопередачи из-за сни-

0 200 400 600 800 1000 1200

Длина, м

Температура, `C

Рис. 4.15. Зависимость распределения температуры по

длине трубопровода от массового расхода жидкости: сни-

зу-вверх – 10, 20, 50, 100, 500, 1100, 3000 т/сут

0 200 400 600 800 1000 1200

Длина , м

Температура, `C

0.0000002

0.0000004

0.0000006

0.0000008

0.000001

0.0000012

0.0000014

0.0000016

0.0000018

0 200 400 600 800 1000 1200

лина

К.вязкость, кв.м/с

9.91

9.92

9.93

9.94

9.95

9.96

9.97

9.98

9.99

0 200 400 600 800 1000 1200

Длина, м

Объемный расход, куб.м/су

)l(q

)l(

)(

244

жения перепада температур. Скорость падения температуры падает до

нуля при сравнивании температуры потока и внешней среды. Так как

объемный расход и вязкость ТС связаны, то нелинейность проявляется

и в зависимостях

)l(q

)l(

– длина от начала звена до уча-

стка –

k).

Рассмотрим зависимость распределения температуры по тому же

звену от изменения массового расхода (см. рис. 4.15). Как видно из

семейства кривых, по мере увеличения

проявление гидротермиче-

ского перехода увеличивается, а проявление передачи тепла во внеш-

нюю среду падает. Причем, существует такое распределение темпера-

тур, что охлаждение потока со стороны внешней среды будет полно-

стью компенсироваться нагревом потока вследствие гидравлического

трения. Для нашего примера в районе от 500 до 1000 т/сут.

Динамическая модель с распределенными параметрами

Здесь рассмат

ривается задача использования описанных выше мо-

делей для условий, когда необходимо сопряжение модели ТГС с моде-

лью гидросистемы продуктивных пластов (ГПП) (см. разделы 4.6 и

4.7). В связи с тем, что исследование ГПП связано с учетом динамиче-

ского (т.е. изменяющегося во времени) распределения гидравлических

и фильтрационно-емкостных свойств пластовой системы необходимо

уч

итывать взаимовлияние ГПП и ТГС.

Как было оговорено граничными условиями модели ТГС являются

давления в активных узлах, которые так или иначе определяют качест-

венное и количественное потоко- и термораспределение.

Для рассмотрения комплексной модели системы ППД необходимо

объединение граничных условий МТГС и модели ГПП. С этой целью

для МТГС удобно в на

иболее простой схеме рассматривать давление в

активных узлах в виде зависимости от времени –

P(t), которая будет

обуславливаться моделью ГПП, а для модели ГПП в качестве гранич-

ного условия удобно задать зависимостью

Q(t) приемистости от вре-

мени для каждого звена – скважины.

В связи с тем, что при воздействии ТГС на ГПП происходит изме-

нение фильтрационно-емкостных свойств коллекторов необходимо

также учитывать динамику проводимостей или замыкающих отноше-

ний

f (q) для призабойных зон пласта (ПЗП) нагнетательных скважин.

Таким образом, следует полагать, что проницаемость ПЗП также

должна описываться зависимостью

k(t), которая будет рассчитываться

в модели ГПП на каждом шаге времени.

245

Описав зависимости

P(t) и k(t),

а также ряд функций, описывающих динамику факторов МТГС

(структурные изменения, износ АСГ, смена УУ и т.п.) при пересчете

комплексного потокораспределения –

КПР во времени, будем иметь

динамику термогидравлического состояния ТГС в виде комплексных

функций

КПР(t), зависящих как от внутренних свойств ТГС, так и от

состояния ГПП. Выбор степени дискретизации фактора времени

определяет точность модели и вид моделей скважин, связывающих

МТГС и модель ГПП. Более подробно это рассмотрено в разделе 4.7.

Описанные модели установившегося потокораспределения можно

использовать также в модели с распределенными параметрами, т.е. с

учетом изменения внутренних свойств элементов ГС в зависимости от

давления, расхода и температуры. Например, такими устройствами,

относящимися к э

лементу УП, являются гидравлические регуляторы

расхода. В зависимости от гидравлического режима, установившегося

в гидросистеме на данный момент, такие устройства изменяют свое

внутреннее состояние некоторым образом с целью изменить гидравли-

ческий режим (см. рис. 3.10 –

а, б). Текущим состоянием таких уст-

ройств будем считать замыкающее отношение

),q(f

звена i, соот-

ветствующего модели этого устройства при текущем факторе

внут-

реннего состояния. Фактором

могут быть, например, высота запор-

ного элемента над седлом или коэффициент местного сопротивления.

Величина

будет изменяться в зависимости от давления или от рас-

хода и температуры в звене

i. Такую зависимость будем описывать

функцией управления по расходу –

)q(

, по давлению

)p(

или по

температуре

)T(

Рассмотрим схему определения состояния гидравлических регуля-

торов и КПР во времени на примере регулятора расхода. Для регуля-

торов расхода управляющим действием будет функция

)q(

, изме-

няющая внутренне состояние регулятора: степень его влияния на по-

ток ТС.

Для нахождения относительной динамики КПР(

L) необходимо за-

даться начальным состоянием звена–регулятора:

)(

для относи-

тельного момента

После нахождения текущего

КПР(L) на момент L состояние звена i

(4.44)

246

изменится:

)q(

)L(

ζζ

, а следовательно изменится замыкающее

отношение

),q(f

)L(

. Далее, определяя следующее КПР(L+1),

получим новое состояния регулятора. При расчете КПР на множество

моментов состояние звена–регулятора стабилизируется, а относитель-

ная динамика – дискретная зависимость

),( Lq

будет является мо-

делью его взаимодействия с гидросистемой. В связи с тем, что в пред-

лагаемых моделях не учитывается фактор времени распространения

гидравлических волн давления в технических гидросистемах, такую

динамику следует считать относительной или условной, так как она не

может показать изменение состояния ТГС во времени. Однако, учет

наличия гидравлических регуляторов в та

ком виде намного более аде-

кватен, чем в моделях с установленными граничными условиями, ко-

гда регулируемый параметр является не зависимой от КПР константой.

Рассмотрим предлагаемые здесь методы численного решения задач

комплексного потокораспределения.

4.4. Численное решение задачи комплексного потокораспределения

в общем виде

Как упоминалось во второй главе, большинство математических

моделей сложных систем решаются численными методами, которые

хотя и дают приближенное решение, но ввиду отсутствия альтерна-

тивных подходов, являются единственными.

Подавляющее большинство численных методов решения систем

нелинейных уравнений сводится к организации так называемого ите-

рационного процесса: процесса последовательных приближений к

корню системы. Для нахождения сл

едующего приближения тем или

иным способом отыскивается некоторое приращение, которое прибав-

ляется или вычитается из предыдущего приближения неизвестных.

В зависимости от способа определения данных приращений чис-

ленные методы отличаются по скорости и устойчивости сходимости к

требуемому корню. Окончанием итерационного процесса считается

выполнение условий, описывающих требуемое достижение решения.

Широкий спектр абстрактных мет

одов численного решения систем

нелинейных систем алгебраических уравнений (СНАУ) сводится к

двум основным группам: I – методы, основанные на линеаризации

функций, входящих в систему (например, «простой итерации», «хорд»

и Ньютона); II – методы, основанные на логических операциях с мно-

247

жеством элементов системы уравнений (метод деления отрезка попо-

лам).

Наиболее эффективными с точки зрения скорости и устойчивости

сходимости считаются методы первой группы. Однако, их применение

зачастую требует адаптации к тому или иному виду СНАУ. Так, для

решения задачи потокораспределения, в зависимости от вида системы

уравнений требуется серьезная доработка методов численного реше-

ни

я. Вследствие того, что СНАУ, описывающие потокораспределение

в произвольных ГС, насыщены замыкающими отношениями произ-

вольного вида, которые также могут изменяться в зависимости от зна-

чений неизвестных непосредственно в итерационном процессе, при-

менение численных методов общего назначения здесь невозможно.

Также недопустима аппроксимация замыкающих отношений типовы-

ми функциями типа

f (q)=r

⋅

, как это делалось в известных ранее мо-

делях [4, 6, 12, …].

В наиболее жесткой, с точки зрения учета массы факторов, поста-

новке задачи комплексного потокораспределения следует полагать,

что метод численного решения модели ГС должен быть таким универ-

сальным, чтобы скорость и надежность сходимости сочетались с при-

менимостью для всего многообразия структур и свойств элементов

роизвольных гидросистем.

Модель течения несжимаемой и сжимаемой жидкости

Рассмотрим предлагаемый здесь численный метод решения систе-

мы уравнений (4.4). Суть метода сводится к линеаризации частей

СНАУ – (4.3), описывающих взаимосвязи замыкающих отношений в

системе линейно-независимых путей. Основой для предлагаемого ме-

тода взят метод Ньютона для систем нелинейных алгебраических

уравнений. Причем, в предлагаемой модели фу

нкции замыкающих

отношений

f(q) могут быть описаны в произвольном виде: табулирова-

ны, рассчитаны «кусочно», заданы алгебраически в виде формул, ап-

проксимированы или интерполированы полиномами или сплайн-

функциями или получены в результате решения дифференциальных

уравнений.

Решение системы (4.4) сводится к последовательному определению

приращений

Δq

ко всем неизвестным расходам q

вектора

на каж-

дом итерационном шаге. Очередное приближение к корню системы

определяется следующим образом:

)I(

qqq

11 ++

Δ+=

(4.45)

248

где

I – номер итерации.

В отличие от метода Ньютона, сходимость которого обусловлена

выбором начального приближения неизвестных

)(

, в предлагаемом

методе начальным приближением следует выбрать

)0(

На каждом итерационном шаге для определения текущих прираще-

ний –

Δq

неизвестных расходов составляется система линейных алгеб-

раических уравнений (СЛАУ) таким образом, чтобы первая часть

(уравнения материального баланса) входила в СЛАУ так же, как и в

исходную систему – (4.2), а вторая часть (уравнения сохранения энер-

гии) в виде частных производных замыкающих отношений –

)I(

)q(f

∂

. Таким образом, на каждом шаге – I решается СЛАУ:

WQJ

⋅

где

J – (матрица урезанный Якобиан) матрица размерностью

, в

которой первые

t строк (соответствующих транзитивным узлам) за-

полняются из строк матрицы соединений

А, соответствующих транзи-

тивным узлам

, а следующие c строк есть произведение вектора произ-

водных замыкающих отношений всех звеньев на матрицу

B системы

путей;

W – вектор правых частей СЛАУ размерностью n: первая часть

вектора (

t строк-элементов) – W

соответствует сумме величин теку-

щих приближений расходов

)(I

потоков звеньев, соединенных с узлом

j (знак перед расходом звена i берется в соответствии со строкой мат-

рицы

), а вторая часть вектора – W

является суммой значений

)(

)(I

звеньев, входящих в путь r, перепада давлений активных уз-

лов, образующих данный путь, и гидростатического перепада актив-

ных узлов данного пути:

UEqf ++−

∑

∈

)(

;

QΔ

– вектор теку-

щих приращений расходов

. В развернутом виде части данной

СЛАУ выглядят следующим образом для узла

j и пути r:

⎪

⎩

⎪

⎨

⎧

++−=Δ

∂

=Δ

∑∑

∈

∈∈

UEqfq

AqAq

)(

)()1(

)(

)()1(

(4.46)

(4.47)

249

где

j – номера транзитивных узлов и соответствующие им строки

матрицы

r – номера путей между активными узлами и соответствую-

щие им строки матрицы

После решения (4.46) любым подходящим методом решения СЛАУ

(например, методом Гаусса) полученные приращения прибавляются к

текущим приближениям неизвестных расходов – (4.45). Поиск прира-

щений повторяется до момента достижения точности.

В распространенной инженерной и специализированной литерату-

ре по высшей вычислительной математике текущая точность (относи-

тельная погрешность) в методе Ньютона определяется следующей за-

висимостью

)I(

поэтому при снижении текущего приращения расхода по звеньям до

выполнения условия

αε

+ )1(I

(

– требуемая минимальная относительная погрешность), процесс

считается завершенным.

Однако, автором выявлено, что такой классический подход к про-

верке текущей точности итерационного процесса не является коррект-

ным, связано это, прежде всего, с тем, что существуют (в качестве ис-

ходных данных модели)

)(

, имеющие экстремумы, отклоняющие

итерационный процесс от правильного решения. В этих случаях теку-

щее приближение

)(I

для некоторых звеньев «западает», т.е. колеб-

лется в районе экстремума (ближайшего к оси абсцисс – расходов).

При этом величины текущих приращений могут быть достаточно ма-

лыми для выполнения условия (4.48) и, следовательно, решение будет

считаться достигнутым, что связано с тем, что «полиэкстремальные»

функции могут многократно пересекать ось абсцисс, а следовательно

система (4.4) может им

еть несколько корней, не все из которых будут

являться правильным решением, хотя и условие (4.48) будет выпол-

няться.

Предлагается способ определения текущей погрешности в итера-

ционном процессе по следующим формулам, которые отражают

действительные требования к результату решения.

(4.48)

250

Погрешность и условие соблюдения точности для первой части

системы (4.4) будет выглядеть как

absQq

∑

∈

)()(

а для второй части, если

≠

()

αϕ

+−

∑

∈

)I(

UE)q(f

если

0=+

()

absPUEqf

<+−=

∑

∈

)(

)()(

Здесь

absQ, absP – величины расходов и давлений, принимаемые в

качестве допущения, как ноль. При соблюдении условий (4.49, 4.50 и

4.51) после решения (4.46) на шаге

I система (4.4) будет считаться ре-

шенной. Интегрирующий коэффициент

)I(

погрешности текущего

приближения можно выразить в виде суммарной невязки перепадов

давлений, полученных из числителя (4.50). Этого будет достаточно,

так как вид первой части систем (4.4) и (4.47) обуславливает незначи-

тельные величины погрешности (связанные только с точностью мето-

да решения СЛАУ) материального баланса, так как соответствует ли-

нейному виду.

Как видно, такой способ вычисления текущей по

грешности заве-

домо исключает возникающие ранее «сбои», однако, потребует допол-

нительных ресурсов ЭВМ, так как возникает необходимость постоян-

ного пересчета моделей всех элементов системы (4.4), т.е. функций

(q).

Еще одним важным моментом адаптации метода Ньютона к по-

ставленной задаче является способ вычисления частных производных,

входящих во вторую часть СЛАУ (4.47), т.е. вычисления выражений

)I(

)q(f

∂

для каждого звена i.

Как показал опыт, характер вычисления производных фактически

является важнейшим фактором сходимости процесса. Это связано с

тем, что существует множество функций, первые производные кото-

(4.49)

(4.50)

(4.51)