Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления
Подождите немного. Документ загружается.

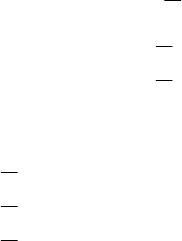
221
ния задать очень просто, и практически возможно это сделать с высо-
кой степенью точности. Например, давление в точке водозабора от-
крытых НТС формируется за счет гидростатического напора, легко
определяемого по известной формуле. Точное определение давления в
герметичных НТС с анизотропной ВС, какими являются пористые
пласты (коллекторы), является уже некоторой проблемой, связанной с
не
обходимостью проведения систематических гидродинамических
исследований на неустановившемся режиме фильтрации (в основном
снятие кривых восстановления/падения давления). Во-вторых, когда
задаются все функции f
i
(q) (модели элементов), описывающие энерге-
тическое влияние элементов. И в-третьих, ни один из расходов q
i
не
может быть фиксированным перед началом решения системы, потому
что в противном случае сама постановка задачи теряет свой смысл
потокораспределения. Это существенным образом отличает данную
МТГС от моделей, предлагаемых в ТГЦ, и для систем газо- и нефтес-
бора и др.
Пример составления системы уравнений. Рассмотрим прежний
пример, схема которого дана на ри
с. 4.5 (для нее m = 6, n = 5 и с = 3).
Первую группу уравнений материального баланса в транзитивных уз-
лах можно получить посредством скалярного произведения 2-й и 3-й
строк матрицы
А на вектор Q и приравнивания их нулю:
s
2
(Q)=q
1
– q
2
=0,
s
3
(Q)=q
2
– q
3
– q
4
– q
5
=0.
Запишем теперь вторую группу уравнений, отражающих энергети-
ческий баланс:
v
1
(Q)= f
1
(q
1
) + f
2
(q
2
) + f
5
(q
5
) – (P
1
– P
4
) –
ρ
g(z
1
– z
2
)=0,
v
2
(Q)= f
1
(q
1
) + f
2
(q
2
) + f
4
(q
4
) – (P
1
– P
5
) –
ρ
g(z
1
– z
5
)=0,
v
3
(Q)= –f
3
(q
3
) + f
4
(q
4
) – (P
6
– P
5
) –
ρ
g(z
6
– z
5
)=0.
Как видно из (4.17), давления в активных узлах 1, 4, 5, 6 должны
быть заданы до решения. Итак, уравнения (4.16) и (4.17) представляют
развернутую систему уравнений для рассматриваемой ТГС.
Метод «узловой увязки» потокораспределения
Наиболее часто используемым при моделировании гидросистем
является метод «поузловой увязки» [48], удобный тем, что для записи
(4.16)
(4.17)
222
системы уравнений нет необходимости в анализе структуры, т.е. поис-
ка системы линейно-независимых контуров или путей. Однако, дан-
ный метод менее точен и с точки зрения скорости вычислений более
медленен, чем известный метод «поконтурной увязки», модификация
которого описывалась выше.
Здесь предлагается новый взгляд на постановку задачи, форму
записи системы у
равнений и метод ее решения. Так как отправной точ-
кой к решению задачи потокораспределения выбрана схема, когда
давления в активных узлах заданы, а приток и отток гидросистемы
определяется в процессе решения, система уравнений записывается
относительно неизвестных давлений в транзитивных узлах. Основным
отличием предлагаемого метода и его математического описания явля-
ется ис
пользование произвольных замыкающих отношений f(q), опи-
санных в табулированном виде или полученных в результате решения
уравнений моделей элементов, вместо аппроксимирующих зависимо-
стей, которые хотя и удобны в использовании, но являются весьма не-
точными.
Основой для системы уравнений является материальный баланс в
транзитивных узлах, выраженный через зависимости
)(
iii
pSq
Δ
=
расхода в звене i от перепада давления на его концах. Функция
(
)
pS
Δ
является обратной функции гидравлической характеристики
)(q
f
,
т.е. для ее определения в произвольной точке –
0
pΔ
необходимо в об-
щем случае решить нелинейное уравнение
(
)
0
0
=
Δ
−
pqf
относитель-
но неизвестного расхода q. Так как при использовании моделей КС,
УУ, АСГ, посредством нахождения перепада давления на гидравличе-
ское сопротивление в зависимости от расхода, установившегося в них,
задающим является расход, то при определении обратной зависимости
p
q Δ−
необходимо численно решать уравнение относительно q при
известном
p
Δ
.
Необходимость в численном решении обусловлена тем, что алгеб-
раически отразить обратную зависимость невозможно хотя бы потому,
что зачастую замыкающие отношения –
)(q
f
задаются «кусочно»:
для различных режимов течения разными формулами. В описываемом
методе подразумевается точное нахождение обратных зависимостей.

223
Опишем поэтапно запись основной системы уравнений данного ме-
тода. Итак, в каждом транзитивном узле должен выполняться матери-
альный баланс
∑
∈
==
ji
i
tjq ,...2,1,0
.
Выразим неизвестные расходы через функции
)(
iii
pSq
Δ
=
, то-
гда получим
∑
∈
==Δ
ji
ii
tjpS ,...2,1,0)(
.
Заменив,
ieib
jji
ppp
−
=Δ
получим уравнения для t транзитивных
узлов, где в каждом уравнении суммируются зависимости
)(
ii
pS
Δ
для звеньев, соединенных (смежных) с транзитивным узлом j.
∑
∈
==−
ji
jji
tjppS
ieib
,...2,1,0)(
,
где j
ib
, j
ie
– начальный и конечный узел звена i.
Причем, давления в транзитивных узлах являются неизвестными, а
давления в активных узлах – константами.
Для отражения влияния гидростатических перепадов в (4.18) необ-
ходимо добавить элементы вектора
Z
:
∑
∈
==Δ+−
ji
ijji
t,...,j,)zpp(S
ieib
210
.
Величина
i
zΔ
для несжимаемой жидкости является константой,
т.е. фактически сдвигает график
)p(S
i
Δ
по оси перепада давления (де-
прессии).
Систему (4.19) перед решением можно привести к классическому
виду, после чего окончательно имеем однородную систему нелиней-
ных алгебраических уравнений (СНАУ) относительно неизвестных
давлений в транзитивных узлах:
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
=
=
=
=
0),,..,,(
0),,..,,(
0),,..,,(
0),,..,,(
21
21
212
211
mjt
mjj
mj
mj
ppppF
ppppF
ppppF
ppppF
M
M
,
(4.18)
(4.20)
(4.19)
224
где
(
)
mjj
ppppF ,..,,..,,
21
– функция зависимости суммы массовых
или объемных расходов потоков, сходящихся в транзитивном узле j, от
давлений в смежных с ним узлах (в том числе и активных). Например,
для схемы на рис. 4.5 схема определения функции F
3
(p
3
, p
2
, P
4
, P
5
, P
6
)
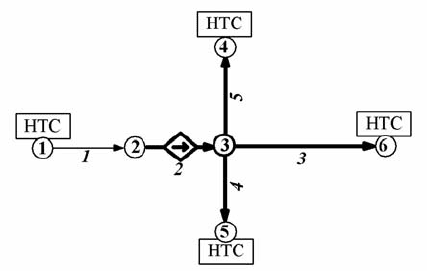
для 3-го (транзитивного узла) отображена на рис. 4.7/1. Как видно,
здесь смежными с 3-м узлом являются транзитивный узел 2 и актив-
ные узлы 4, 5, 6, а звеньями, обуславливающими взаимосвязь, являют-
ся звенья с номерами 2, 5, 4 и 3. Таким образом, отношениями, опре-
деляющими F
3
, будут функции S
2
(p
2
– p
3
), S
5
(p
3
– P
4
), S
4
(p
3
– P
5
) и S
3
(p
3
–
P
6
). Причем, при определении депрессий первым всегда берется дав-
ление в узле начала звена согласно его ориентации, а знак перед функ-
циями S ставится согласно ориентации звена по отношению к транзи-
тивному узлу. Так, для примера на рис. 4.7/1:
F
3
(p
3
, p
2
, P
4
, P
5
, P
6
)= S
2
(p
2
– p
3
+ Δz
2
) – S
5
(p
3
– P
4
+ Δz
5
) –
S
4
(p
3
– P
5
+ Δz
4
) – S
3
(p
3
– P
6
+ Δz
3
).
Рис. 4.7/1. Схема определения функции F
3
(p
3
, p
2
, P
4
, P
5
, P
6
)
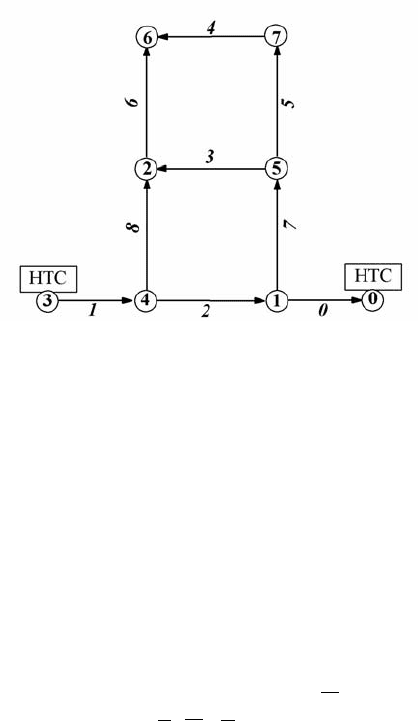
Рассмотрим пример на рис. 4.7/2, где изображена относительно
простая схема гидросистемы. Как видно из схемы, она представлена
9-ю структурно-связанными звеньями, 2-я активными узлами и 6-ю
транзитивными узлами. Структура схемы является цикло-
древовидной.
(4.20а)
225
Рис. 4.7/2. Пример схемы ГС
Запишем систему уравнений на основании (4.19) для каждого тран-
зитивного узла:
07
06
05
04
02
01
46745755
46746626
751757553253
824821421431
824866263253
214275170010
=Δ+−−Δ+−
=Δ+−+Δ+−
=Δ+−+Δ+−−Δ+−−
=Δ+−−Δ+−−Δ+−
=Δ+−+Δ+−−Δ+−
=
Δ
+
−
+
Δ
+
−
−
Δ
+
−−
)zpp(S)zpp(S:
)zpp(S)zpp(S:
)zpp(S)zpp(S)zpp(S:
)zpp(S)zpp(S)zpP(S:
)zpp(S)zpp(S)zpp(S:
)zpp(S)zpp(S)zPp(S:
Здесь знак перед функциями S
i
выбирается исходя из ориентации
звеньев в структуре: если звено входит в узел, знак «+», если выходит,
знак «–».
В матрично-векторном представлении система (4.19) будет выгля-
деть следующим образом относительно вектора неизвестных давлений
в транзитивных узлах, связанных с определением
Y
′
.
A⋅
S
(
Y
′
+
Z
) = 0,
а для каждого транзитивного узла j
∑
∈
=Δ+−
ji
ijjiji
)zpp(Sa
ieib
0
,
где
∑
∈ ji
– означает суммирование по звеньям инцидентным узлу j.
(4.21)
(4.22)
(4.23)
226
Системы (4.19), (4.22) и (4.23) могут быть модифицированы для
случая, когда в качестве граничных условий все-таки необходимо за-
дать приток или отток из гидросистемы. В этом случае в правую часть
уравнений вместо нуля ставится константа, символизирующая приток,
если >0 или отток, если <0. Если описать вектор притоков/оттоков ТС
в узлах
=
X
,
то система (4.22) примет вид
A
S
(
Y
′
+
Z
) =
X
,
а система (4.23)
∑
∈
=Δ+−
ji
jijjiji
x)zpp(Sa
ieib
.
В случае, когда необходимо явно указать приток/отток в активных
узлах, давления в них становятся так же, как и в транзитивных узлах
неизвестными. Для задачи проектирования ТГС такие граничные ус-
ловия допустимы, однако, для уже существующих гидросистем при
решении задачи по их управлению такие условия недопустимы, так
как в этом случае мод
ель не будет отражать истинных реакций систе-
мы на изменение свойств ее элементов.
Данный подход к формированию системы уравнений, как и в мето-
де «поузловой увязки», является более универсальным, так как не тре-
бует предварительного анализа структуры, однако многократное вхо-
ждение в систему уравнений, обратных исходным нелинейным замы-
кающим отношениям, п
орождает проблемы устойчивости и точности
ее численного решения.
Рассмотрим математическое описание для задачи комплексного по-
токораспределения при условиях установившегося течения сжимае-
мой жидкости или газа.
Вследствие решения задачи потокораспределения относительно
неизвестных расходов метод «путевой увязки» в явном виде не подхо-
дит для нахождения потокораспределения, когда свойства текучей
x
1
x
2
..
x
j
..
x
m
(4.24)
(4.25)

227
среды зависят от давления. Поэтому для описания комплексного пото-
кораспределения будем использовать метод узловой увязки.
Для описания условий сжимаемости текучей среды необходимо
функционально определить зависимость физических свойств среды,
влияющих на распределение потоков от давления. Для этого зададимся
функциями
)p
(
ρ
– зависимости плотности от давления и
)p
(
ν
– за-
висимости кинематической вязкости от давления. Исходя из измене-
ний данных свойств по длине любого звена, функции замыкающих
отношений f
i
(q), связывающих перепад давления на концах звеньев и
объемный расход, уже не будут достаточными для определения обрат-
ных им функций
)p(S
ii
Δ
, так как объемный расход в звене будет из-
меняться.
Таким образом, для рассматриваемой задачи необходимы другие
замыкающие отношения: функции
)z,z,p,p(S
ieibieib
jjjji
′
, связывающие
массовый расход М
i
, давления и отметки высот концов звеньев. Под-
ставив данные функции в (4.23), получим систему из уравнений вида
∑
∈
=
′
ji
jjjjiji
)z,z,p,p(Sa
ieibieib
0
,
где
ib
j
z
,
ie
j
z
– абсолютные отметки положения узлов начала и
конца звена i относительно отсчетной плоскости.
Если задать вектор абсолютных отметок всех узлов
=
V
,
то в матрично-векторном представлении (4.26) будет
A⋅ S
′
(
P
,
V
) = 0.
Для нахождения зависимостей
)z,z,p,p(S
ieibieib
jjjji
′
при формиро-
вании модели каждого звена необходимо численно решить уравнение,
связывающее массовый расход в звене i с давлениями на его концах.
Прибегнем к вычислительному приему: разделим звено i на N частей.
Будем нумеровать каждый участок звена индексом k, начиная от узла
начала (см. рис. 4.8).
(4.26)
(4.27)
z
1
z
2
..
z
j
..
z
m

228
Рис. 4.8. Схема расчета для условий сжимаемости ТС
На каждом малом участке звена –
N
l
l =Δ
будем полагать величины
плотности и кинематической вязкости постоянными, т.е. не зависящи-
ми от изменения давления. Рассматривая функцию зависимости пере-
пада давления на участке
l
Δ
звена i от массового расхода в звене M
i
,
плотности
ρ
и кинематической вязкости
ν
на этом участке в виде
функции
f
i
(M
i
,
ρ
,
ν
, Δl), получим следующее соотношение:
ieib
jjN
N
k
kkkiiii
pppp)z,l,,,M(f)M(w −=−=ΔΔ=
∑
=
0
1
νρ
,
где
kii
k
qM
ρ
=
– массовый расход в звене, равный произведению
объемного расхода на участке
k на плотность;
()
k
k
p
ρρ
=
– средняя плотность на участке k;
()
k
k
p
ν
ν
=
– средняя кинематическая вязкость на участке k;
g
l
zz
lg
N
zz
z
k
N
k
N
k
ρρ
−
Δ=
−
=Δ
00
– гидростатический пе-
репад давления на участке
k.
Здесь
2
1−
+
=
kk
k
pp
p
– среднее давление на участке k. Давления к
началу следующего участка определяются последовательно, на осно-
вании замыкающих отношений (4.1) (моделей элементов) для несжи-
маемой ТС:
kkkiikk
z)l,,,q(fpp
k
Δ
+
Δ
−
=
−
ν
ρ
1
. Величина Δl опре-
деляет деление доли энергетического воздействия звена на участки:
секции насосных агрегатов, участки трубопроводов и т.п.
Величина
N определяет точность и может быть определена при-
ближенно по формуле для трубопроводов
Δ=
г
d
l
N 100
, где d
г
– гид-
(4.28)
229
равлический диаметр, а
Δ
– относительная шероховатость. Также для
всей модели
N можно принять с запасом, равным 1000–10000.
При решении (4.28) в момент нахождения входящей в (4.26–4.27)
)z,z,p,p(S
ieibieib
jjjji
′
величины p
0
, z
0
и p
N
, z
N
являются константами,
однозначно определяющими вид зависимости от
M
i
слева. Таким обра-
зом, функцию
)M(w
ii
посредством численного решения можно об-
ратить, т.е. решить относительно неизвестных давлений в виде функ-
ции
)z,z,p,p(SM
ieibieib
jjjjii
′
=
.
Порядок расчета
)M(w
ii
зависит от соотношения направления
потока и ориентации звена. Так, при противоположном ориентации
звена потоке последовательность расчета
p
k
следует начинать с узла –
конца звена, так как причинно-следственная связь прослеживается со-
гласно направлению потока. Вследствие такой неоднозначности, вид
функций
)z,z,p,p(S
ieibieib
jjjji
′
бу-
дет несколько изменяться при
последовательном приближении
потокораспределения в ходе чис-
ленного решения (4.26–4.27).
Рассмотрим порядок прибли-
женного получения зависимости
)z,z,p,p(S
ieibieib
jjjji
′
на примере
звена – трубопровода.
В целях упрощения задачи
допустим, что модель (замыкаю-
щее отношение
Δp=f(q) ) данного
трубопровода в условиях устано-
вившегося течения несжимаемой
жидкости записывается в виде
функции
q
eqlp
100
100 ⋅⋅⋅⋅=Δ
ν
.
Предположим, что данное уравнение относительно
q алгебраически
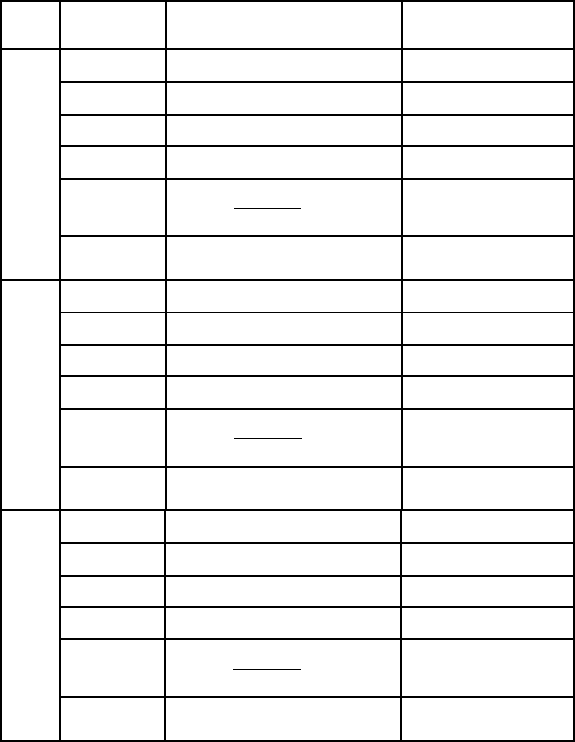
решить невозможно. Сведем исходные данные задачи в табл. 4.1.
Предположим зависимость
p.)p( 101000+
=
ρ
, а зависимость
p
..)
p
(
0000100010 −=
ν
. Разделим наше звено на N = 4 частей, помня,
что в реальных моделях число
N зависит от степени влияния звена на
энергию потока. Допустим, что направление потока соответствует
ориентации звена.
Таблица 4.1. Исходные величины
Величина
Ед.
изм.
Значение
p
0
МПа 21.0
p
4
МПа 10.0
z
0
м 100
z
1
м 10
l м 2000
M
0
кг/с 10
M
1
кг/с –
M
2
кг/с –
230
Таблица 4.2. Пример расчета распределения давлений в звене
Шаг
k=
Величина Формула Значение
1
ρ
, кг/м
3
01
101000 p.
+
=
ρ
1002.1
1
ν
, м
2
/с
01
0000100010 p..
−
=
ν
0.00078
q
1
, м
3
/с
101
ρ
/Mq
=
9.979⋅10
–3
1
pΔ
, МПа
1
100
11
100
q
elqp
ν
=Δ
0.398
1
zΔ
, МПа
6
1
0
1
10
−
⋅
−
=Δ g
N
zz
z
N
ρ
0.221
1
p
1
, МПа
1101
zppp Δ
+
Δ
−
=
21.00–
0.398+0.221=20.823
2
ρ
, кг/м
3
12
101000 p.
+
=
ρ
1002.08
2
ν
, м
2
/с
12
0000100010 p..
−
=
ν
0.00079
q
2
, м
3
/с
202
ρ
/Mq
=
9.979⋅10
–3
2
pΔ
, МПа
2
100
22
100
q
elqp
ν
=Δ
0.399
2
zΔ
, МПа
6
2
0
2
10
−
⋅
−
=Δ g
N
zz
z
N
ρ
0.221
2
p
2
, МПа
2212
zppp Δ
+
Δ
−
=
20.823–
0.399+0.221=20.645
3
ρ
, кг/м
3
23
101000 p.
+
=
ρ
1002.07
3
ν
, м
2
/с
23
0000100010 p..
−
=
ν
0.00079
q
3
, м
3
/с
303
ρ
/Mq
=
9.979⋅10
–3
3
pΔ
, МПа
3
100
33
100
q
elqp
ν
=Δ
0.400
3
zΔ
, МПа
6
3
0
2
10
−
⋅
−
=Δ g
N
zz
z
N
ρ
0.221
3
p
3
, МПа
3323
zppp Δ
+
Δ
−
=
20.645–
0.4+0.221=20.466
Для нахождения необходимой зависимости нужно найти давление
на выходе из звена при различных величинах массового расхода:
M
0
,
M
1
, M
2
и т.д. В табл. 4.2 приводятся примеры расчета давлений при
переходе от участка к участку.
