Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления
Подождите немного. Документ загружается.

271
4.5. Модели элементов технических и природных гидросистем
Элементом моделей неизотермического течения несжимаемых ТС
являются зависимости вязкости и плотности от давления и температу-
ры, которые необходимо рассчитывать при решении комплексного
потокораспределения. Рассмотрим модели ТС на примере жидкости –
воды для систем ППД.
Модель рабочей жидкости систем поддержания пластового
давления
Известно, что основные физические свойства жидкостей и газов –
плотность и вязкость зависят от термобарических условий, т.е. зависят
от давления и температуры.
Для воды, используемой в системах ППД, автором предлагается
эмпирическая формула определения плотности воды в зависимости от
давления и температуры
pTTp
p
4306.0009.026.1000),(
0002135.0837.1
+−=
−
ρ
,
где
p – давление ТС, МПа;
T –температура ТС,
0
C;
ρ
– плотность, кг/м
3
.
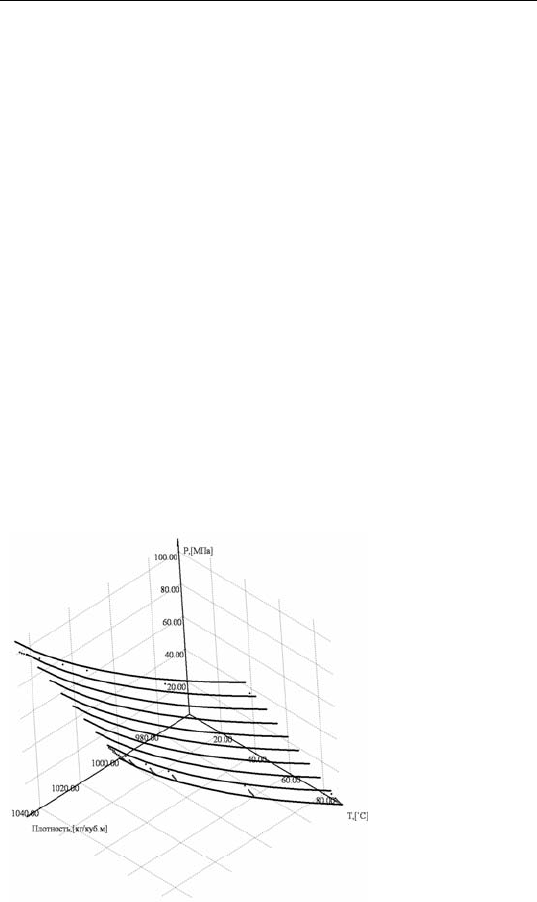
Полученная поверхность (см. рис. 4.24) имеет сумму квадратов от-
клонений по экспериментальным точкам, равную 28.6 (кг/м
3
)
2
, и отно-
сительное среднеарифметическое отклонение 0.38%
Рис. 4.24. Зависи-
мость плотности
от давления и тем-
пературы (точками
показаны фактиче-
ские замеры)
(4.66)
272
Для определения кинематической вязкости предлагается следую-
щая формула:
2380031310
00138057781
18460
.T.
T
.
p
e
.
.)T,p( −+=
⋅
ν
,
где p – давление ТС, МПа;
T – температура ТС,
0
C;
ν
– кинематическая вязкость мм
2
/с.
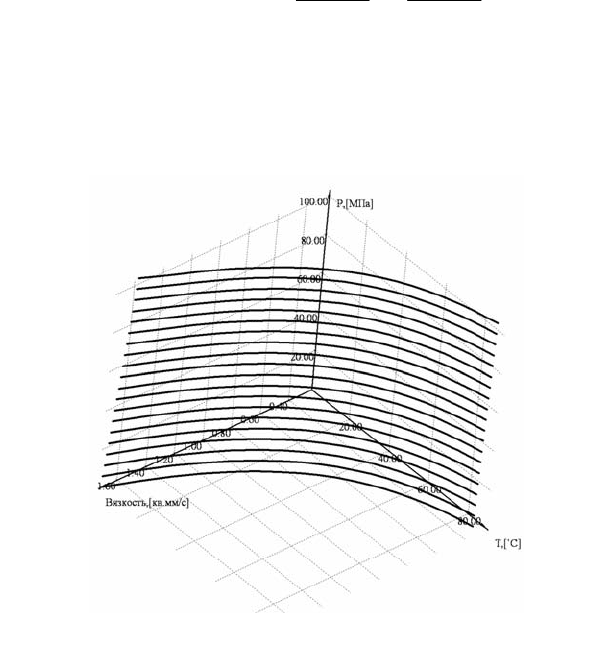
Полученная поверхность (см. рис. 4.25) имеет сумму квадратов от-
клонений по экспериментальным точкам, равную 0.12 (мм
2
/с)
2
, и отно-
сительное среднеарифметическое отклонение 0.88%.
Интервалом применимости формул (4.66, 4.67) являются темпера-
тура в пределах от 0 до 99
о
С и давление от 0.1 до 100 МПа.
Рассмотрим задачу, стоящую в нахождении функций f
i
(q), отра-
жающих воздействие конкретных объектов ГС и/или их частей f
i
(q,Δl)
на энергию пропускаемого ими потока, в зависимости от их внутрен-
них свойств не связанных
признаком системы.
Рис. 4.25. Зависимость кинематической вязкости от давления
и температуры (точками показаны фактические замеры)
(4.67)
273
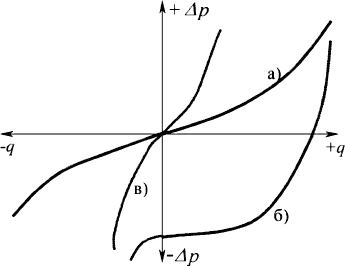
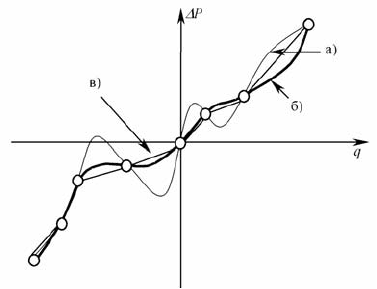
Рис. 4.26. Некоторые формы функций f(q) для
различных объектов ТГС:
а – объект «труба»;
б – объект «насос», электропитание включено;
в – объект «насос», электропитание выключено
Модель объектов, описываемая посредством явного задания
полной гидравлической характеристики
Гидравлическое моделирование отдельных объектов (конкретных
устройств, представляющих элементы) ГС в рамках поставленной за-
дачи сводится к опреде-
лению перепада давле-
ния между входом в
звено (или его части) и
выходом из него в зави-
симости от технических
(внутренних природ-
ных) свойств – пара-
метров объекта. Иначе
говоря, целью такого
моделирования является
нахождение зав
исимо-
сти
)(
iii
qfp =
′
Δ
между величиной объ-
емного расхода текучей
среды сквозь звено i
(объект ТГС) – q
i
и пе-
репадом давления на его концах, зависящей от некоторых параметров
звена, не связанных признаком системы. Перепад давления
i
p
′
Δ
, зави-
сящий от таких параметров звеньев/объектов, это та часть общего пе-
репада давления, которая имеет зависимость от расхода. Остальная
составляющая Δz
i
перепада Δp
i
не имеет зависимости от расхода, и
поэтому рассматриваться в данном разделе не будет. Далее перепад
i
p
′
Δ
будем обозначать просто
i
pΔ
. Итак,
i
pΔ
есть разность между
давлением на входе в звено i и давлением на выходе из него, т. е. знак
i
pΔ
строго зависит от ориентации звена, его влияния на энергию по-
тока текучей среды и направления течения потока.
В зависимости от свойств объекта кривые f (q) могут иметь различ-
ные формы, которые, прежде всего, зависят от характера воздействия
объекта на текучую среду и значений тех или иных его геометриче-
ских или физических п
араметров.
На рис. 4.26 представлены некоторые формы функции f (q).
274
Все объекты, представляющие те или иные элементы гидросистем с
позиции влияния на энергию проходящего сквозь них потока текучей
среды можно разделить на две группы:
1– объекты, изменяющие энергию потока в положительную сторо-
ну, такими объектами являются АС.
2 – объекты, отнимающие энергию потока, такими объектами яв-
ляются УУ, КС и АП.
Эти г
руппы в полной мере отражаются в полной гидравлической
характеристике, т.е. в функциях Δp
b-e
=f (q). Ранее под гидравлической
характеристикой элементов гидросистем было принято понимать лишь
часть линий f(q), описывающих рабочий режим, причем, например, для
труб гидравлической характеристикой связывался перепад давления
между входом и выходом с расходом потока (q > 0), а для насосов пе-
репад давления между выходом и входом с расходом (q > 0). Если вы-
де
ление рабочей характеристики насосных агрегатов еще можно по-
нять, то для КС, УУ
это понятие не мо-
жет быть примене-
но, ввиду того, что
они действуют в
обоих направлени-
ях, т.е. при 0< q< 0.
Поэтому необ-
ходимо определить
наиболее адекват-
ный универсальный
подход к моделиро-
ванию всех элемен-
тов
г
идросистем,
который позволит
рассчитывать замы-
кающие отношения
Δp
b-e
=f(q) макси-
мально приближенно к обще-энергетическим и физическим аспектам
работы различных объектов ГС. На рис. 4.26 показаны примеры пол-
ных гидравлических характеристик [кривых f (q)] типичных объектов
ТГС. Рассмотрим наиболее распространенный объект ТГС – «труба».
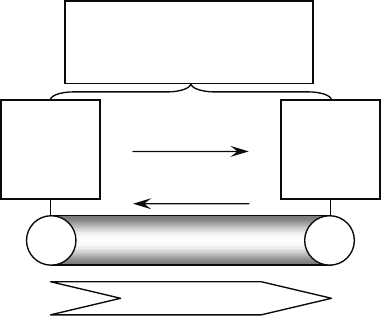
Как видно из рис. 4.26 и схемы на рис. 4.27, при совпадении направле-
ния потока с ориентацией звена он и
меет положительный знак, т.е.
ЗВЕНО–
i
j
ib
j
ie
ориентация
Давление в
узле начала(b)
звена
ib
j
p
Давление в
узле конца(e)
звена
ie
j
p
Перепад давления меду узлом начала
j
ib
и конца j
ie
звена
Δ
p
b-e
=f
i
(q)
q>0
q<0
Рис. 4.27. Схема определения замыкающих от-
ношений
f(q) произвольного объекта-звена МТГС
275
поток заходит в трубу со стороны узла начала трубы – j
b
, и вследствие
того, что все КС отнимают энергию потока (из-за гидравлических со-
противлений) давление в узле конца трубы – j
ie
будет меньше, чем в j
ib
.
Отсюда следует, что перепад давления Δp
b-e
будет положительным, а
кривая f(q) при q>0 лежит в первой четверти числовой плоскости Δp–q
(см. рис. 4.26 – a). При этом потребляемая гидравлическая мощность,
рассеиваемая звеном
qpN
eb−
Δ= => N>0.
Если направление потока не совпадает с ориентацией звена (q < 0),
то поток входит в звено из узла конца – j
ie
и, теряя давление в звене,
выходит в узел начала j
ib
с давлением, меньшим давления в j
ie
. Таким
образом, перепад давления Δp
b-e
будет отрицательным, а потребляемая
гидравлическая мощность звена будет положительной, что подтвер-
ждает адекватность рассматриваемой f (q) физике процесса.
Перейдем к более сложному объекту – «насос» (см. рис. 4.26–б).
Согласно своей ориентации, при нормальном режиме работы АСГ соз-
дает условия, в которых при совпадении направления потока с ориен-
тацией звена давление в уз
ле j
ib
всегда меньше давления в узле j
ie
, и
следовательно, величина Δp
b-e
<0. Потребляемая гидравлическая мощ-
ность «насоса» в таком режиме будет отрицательной (т.е. насосный
агрегат не потребляет, а вырабатывает гидравлическую мощность). В
ТГС при авариях возможны случаи, при которых направление потока в
насосных агрегатах (даже с подводом энергии) может быть противо-
положно их ориентации. При этом q < 0, а давление в узле j
ib
так же,
как и при рабочем режиме меньше, чем в j
ie
, а кривая f(q), описываю-
щая данный режим располагается в третьей четверти. Потребляемая
гидравлическая мощность звена в этом случае будет больше нуля. Т.е.
насосный агрегат работает на режиме «гидравлического тормоза» (см.
далее объект «насос»). Существует еще один режим работы насосных
агрегатов, который описывается продолжением рабочей части f (q) в
первую ч
етверть плоскости Δp – q. Здесь описывается случай превы-
шения величины расхода q над максимальной производительностью
насосного агрегата, при этом q > 0, а давление в узле j
ib
больше давле-
ния в j
ie
. В этом режиме потребляемая звеном гидравлическая мощ-
ность положительна.
Из вышеизложенного следует, что предлагаемый порядок построе-
ния эмпирических или теоретических гидравлических характеристик
f (q) любых объектов ГС помимо четкой формализации при построе-
нии универсальной модели гидравлических систем дает единый и эф-
(4.68)
276
Рис. 4.28. Интерполирование f(q) по произволь-
но разбросанным в плоскости ΔP–q точкам: а –
пример интерполяции (
P
8
); б – пример интерпо-
ляции по предлагаемой схеме (
P
3
); в – пример
интерполяции по предлагаемой схеме (
P
1
)
фективный подход к анализу свойств элементов ГС, а также позволяет
проводить адекватную энергетическую оценку функционирования
объектов без необходимости знания их технических и природных ха-
рактеристик.
Рассмотрим общую методологию наиболее универсального описа-
ния функций f (q) по табулированным эмпирическим зависимостям
перепада давления и расхода жидкости.
Что касается необходимых формальных требований к виду f (q), от-
веч
ающих наиболее общим физическим свойствам установившегося
течения жидкости, а также исходным положениям математического
моделирования ГС, то они сводятся к единственному условию:
непрерывности и желательно гладкости, т.е. существованию не-
прерывных производных
)(qf
′
на всей числовой оси –∞ < q < +∞.
Как видно из (4.14, 4.25) и алгоритмов на рис. 4.16, 4.21, при расче-
те потокораспределения ГС наиболее часто возникает задача опреде-
ления f (q). Допустим, что у нас имеется информация о форме данной
функции в виде множеств числовых значений x
i
, соответствующих
расходу q и y
i
,
соответствующих
перепаду давления
Δp
b-e
в некоторых n
точках, т.е. i=0, 1, 2,
..., n–1.
Тогда для нахож-
дения f(q) в точке q=X
следует произвести
аппроксимацию или
интерполяцию имею-
щихся данных поли-
номом m-й степени
(P
m
), где m может
быть меньше либо
равно количеству
точек n, в которых
заданы x
i
и y
i
.
Известно, что процесс
интерполяции m-й степени для m>>3 отнимает у ЭВМ недопустимо
много времени, при условии многократной повторяемости таких рас-
четов. Более того, при интерполяции полиномом высокой степени мы
277
получаем серьезные биения функции между заданными точками (см.
рис. 4.28 – а).
Здесь предлагается упрощенная схема определения f(q), благодаря
применению которой существенно экономится время расчета на ЭВМ,
что очень важно при решении потокораспределения крупных ГС.
Отличие данной схемы от схемы, применяемой при обычной ин-
терполяции, заключается в интерполяции не всего объема точек (x
i
,y
i
),
а только тех, которые входят в определенный интервал, выбранный в
зависимости от X, и степени локальной интерполяции. Под локальной
интерполяцией понимается интерполяция между необходимой частью
всех заданных точек. Данная схема имеет некоторое сходство с интер-
полированием сплайнами, однако, здесь нет необходимости решать
систему уравнений для условий равенства производных, что сущест-
венно эк
ономит ресурсы ЭВМ.
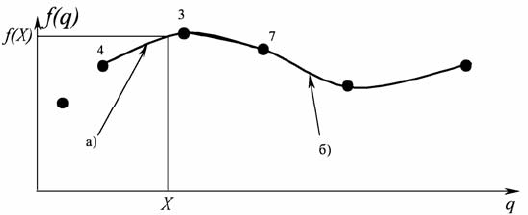
Рассмотрим пример, продемонстрированный на рис. 4.29. Функция
f(q) представлена произвольным количеством точек, разбросанных на
числовой плоскости Δp–q. Для определения значения f (q) в некоторой
точке X при выбранной квадратичной локальной интерполяции выби-
раются 3 ближайшие к ней точки, опираясь на которые, путем интер-
поляции полиномом P
2
находится искомое значение f (X). Опорные
точки выбираются следующим образом: чиcло X попадает между дву-
мя точками с номерами, например, 4 и 3, и так как степень интерполя-
ции равна 2, то выбирается следующая за ними точка, например, с но-
мером 7. Таким образом, интерполируется участок от точки 4 до точки
7.
Процесс последовательного нахождения значений f (q) при x
0
<q<x
n-
1
будет сопровождаться постепенной сменой опорных точек. Что каса-
Рис. 4.29. Пример интерполяции по предлагаемой схеме:
а – степень
локальной интерполяции – 2 (
P
2
); б – степень локальной интерполяции
– 3
(
P
3
)

278
ется локальной интерполяции P
3
, то выбор интервалов происходит
аналогично P
2
с той лишь разницей, что к трем уже имеющимся опор-
ным точкам (P
2
) добавляется еще одна.
Необходимость в применении такой схемы нахождения f (q) объяс-
няется тем, что форма типовых функций весьма разнообразна, начиная
от простой для трубопроводов и штуцеров и заканчивая достаточно
сложной для регуляторов расхода и насосных агрегатов. Если взять в
качестве примера часто используемую полную характеристику ЦНС,
применяемого в системах ППД, то можн
о убедиться в том, что такой
вид функции невозможно достаточно точно интерполировать полино-
мом 3-й или даже 5-й степени.
Поэтому предлагаемая схема оказывается в такой ситуации незаме-
нимой с точки зрения экономии машинного времени и для большинст-
ва функций f(q) является предпочтительней применения сплайнов.
В отличие от сплайнов н
едостатком данной схемы является вероят-
ность возникновения мест «узловых стыков», когда значение частной
производной
()
i
x
q
f
∂
∂
в x
i
изменяется при смене интервала выбора то-
чек. Однако, для количества дискретных значений более 10 данная
схема удовлетворяет точности расчета. Тем не менее, условие точно-
сти можно соблюсти, интерполировав исходный массив точек по
предлагаемой схеме полиномом P
3
, а затем создать новый массив то-
чек с необходимым шагом по оси q, но уже линейной интерполяцией.
Это позволит избежать проблем сходимости в процессе решения ос-
новной системы уравнений.
Иначе данную задачу можно решить посредством аппроксимации
или интерполяции заданного массива точек полиномом m-й степени.
Рассмотрим наиболее универсальный метод аппроксимации мето-
до
м наименьших квадратов полиномом m-й степени
m
mm
xaxaaxQ +++= ...)(
10
.
Для этого зададим постоянные коэффициенты:
n
k
n
kk
k
k
n
kk
k
yxyxyxt
kxxxS
...
,...2,1,0,...
1100
10
++=
=+++=
Преобразуя систему (m+1) уравнений и используя эти обозначения,
получим систему линейных уравнений относительно неизвестных ко-
эффициентов a
0
, a
1
,…, a
m
:
(4.69)

279
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=+++
=+++
=+++
=+++
+
+
+
mmmmm
mm
mm
mm
tSa...SaSa
tSa...SaSa
tSa...SaSa
tSa...SaSa
2110
223120
112110
01100
Решая данную систему, например, методом Гаусса получим коэф-
фициенты полинома заданной степени. Причем, при выборе степени
полинома m, равной количеству исходных точек n получим интерпо-
ляцию, т.е. точное прохождение функции
)(xQ
m
через n заданных
точек.
Данный метод позволяет находить полином любой степени, одна-
ко, слишком большое значение m серьезно замедлит расчет и приведет
к непредсказуемому поведению f (q) (см. рис. 4.28 – а).
Как показывает опыт аппроксимации и интерполяции эмпириче-
ских гидравлических характеристик, поведение функции f (q) за пре-
делами (x
0
, x
n–1
) отражается наиболее адекватно при условии нечетно-
сти степени полинома.
Далее мы подробно остановимся на моделировании отдельных
объектов (элементов) ТГС при условии течения несжимаемой жидко-
сти исходя из теоретического многофакторного определения полных
гидравлических характеристик – функций f (q).
Для распространения описываемых далее моделей на условия не-
изотермического течения сжимаемой жидкости можно использовать
следующий чи
сленный прием приближенного определения
)M(f
ii
,
который, в общем, был рассмотрен ранее.
Для определения зависимости перепада давления на концах звена
при текущем термораспределении на каждом участке k звена i пола-
гать постоянство объемного расхода
k
i
q
, давления
k
i
p
, температуры
k
i
T
, вязкости
)T,p(
kkk
iii
ν
ν
=
и плотности
)T,p(
kkk
iii
ρ
ν
=
. Тогда
суммарный перепад давлений на концах звена будет складываться из
перепадов давления на каждом из N участков
[]
∑
=
⋅Δ+
=
=
=−
N
k
iiiiiiiii
iijj
N
g)T,p(z)T,p(),T,p(,qf
)M(fpp
kkkkkkk
ieib
1
ρρν
,
(4.70)
(4.71)
280
где
k
i
zΔ – гидростатический перепад на участке k звена i.
Разумеется под функцией f
i
(q
i
) понимается зависимость перепада
давления от объемного расхода при изотермическом течении несжи-
маемой ТС, а под
)M(f
ii
– зависимость перепада давления от массо-
вого расхода при изотермическом или неизотермическом течении сжи-
маемой ТС. Таким образом, эти функции различны, а использование в
уравнениях и формулах одинакового символа – f конкретизируется
аргументом: если q
i
, то имеется в виду изотермическое течение не-
сжимаемой ТС, а если M
i
, то имеется в виду течение сжимаемой жид-
кости с возможным учетом термораспределения. Характер определе-
ния и использования этих замыкающих отношений зависит от вида
системы уравнений, как это показано в разделах 4.3 и 4.4.
Модели трубопроводов
Трубы используются в ТГС повсеместно, и могут являться частью
более сложных объектов, таких как, например, «скважина». Точное
моделирование данного объекта является очень важным и зачастую
решающим ввиду его доминирующего количества в ТГС.
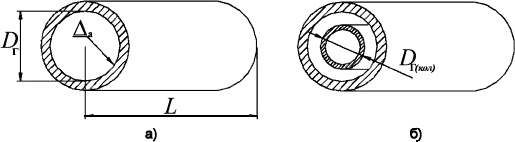
В предлагаемой модели под «трубой» понимается элемент ГС – ка-
нал связи, у которого в качестве изолирующей искусственной или ес-
т
ественной системы используется твердый непроницаемый корпус
цилиндрической формы (см. рис. 4.30).
Необходимость в выделении двух типов данного объекта объясня-
ется спецификой систем ППД. Как отмечалось раннее, объект «труба»
входит в состав более сложного объекта «скважина». Известно, что
при закачке воды в пласт со сравнительно небольшими приемистостя-
ми (до 500 м
3
/сут) используются насосно-компрессорные трубы (НКТ).
Рис. 4.30. Сечения объекта «труба»:
а – простая цилиндрическая
труба; б – кольцевая труба (труба в трубе), течение по кольцевому и
центральному пространству
