Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

CONTEXTS

534 CHAPTER 6

■

Power, Polynomial, and Rational Functions

9–12 ■ Graph the family of functions in the same viewing rectangle, using the given values

of c. Explain how changing the value of c affects the graph.

9. 10.

11. 12.

13–20

■ Sketch a graph of the given function.

13. 14.

15. 16.

17. 18.

19. 20.

21–24

■ Write an equation that expresses the statement.

21. P is inversely proportional to T.

22. R is inversely proportional to the third power of c.

23. y is inversely proportional to the square root of t.

24. E is inversely proportional to the fourth root of t.

25–28

■ Express the statement as an equation. Use the given information to find the

constant of proportionality.

25. is inversely proportional to t. If t is 3, then is 2.

26. R is inversely proportional to s. If s is 4, then R is 3.

27. s is inversely proportional to the square root of t. If t is 9, then s is 15.

28. W is inversely proportional to the square of r. If r is 6, then W is 10.

29–30

■ Use the given information to solve the problem.

29. is inversely proportional to the cube of x. If the constant of proportionality k is 1.5,

then find when x is 2.

30. C is inversely proportional to the square of t. If the constant of proportionality k is 5,

then find C when t is 7.

31. Boyle’s Law The pressure P of a sample of oxygen gas that is compressed at a

constant temperature is inversely proportional to the volume of gas.

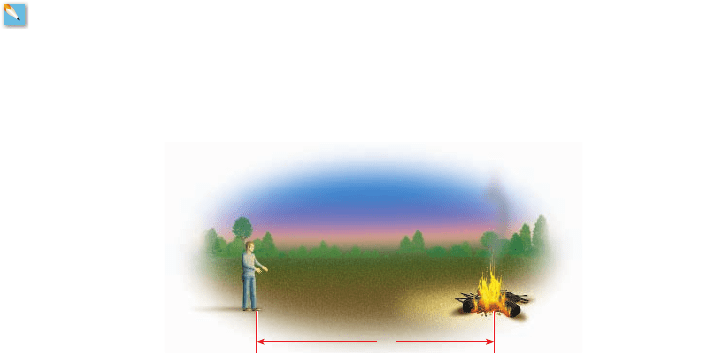
(a) Find the constant of proportionality if a sample of oxygen gas that occupies

exerts a pressure of 39 kPa at a temperature of 293 K (absolute

temperature measured on the Kelvin scale). Write the equation that expresses the

inverse proportionality.

(b) If the sample expands to a volume of , find the new pressure.

32. Skidding in a Curve A car weighing 1000 kilograms is traveling at a speed of

15 meters per second on a curve that forms a circular arc. The centripetal force F that

pushes the car outward is inversely proportional to the radius r (measured in meters) of

the curve.

(a) If the curve has a radius of 90 meters, then the force required to keep the car from

skidding is 2500 newtons. Write an equation that expresses the inverse proportionality.

(b) The car will skid if the centripetal force is greater than the frictional force holding the

tires to the road. For this road the maximum frictional force is 5880 newtons. What is

the radius of the tightest curve the car can maneuver before it starts slipping?

0.916 m

0.671 m

f 1x 2=

- 1f 1x 2=

+ 1

f 1x 2=

f 1x 2= 2x

-7

f 1x 2= 5x

-4

f 1x 2= 10x

-2

f 1x 2= 3x

-1

G1x 2= x

-2

+ c;c =-1, 0, 1, 2F 1x 2= cx

-1

;c = 1, 2, 5,

g1x 2= x

-c

;c = 2, 4, 6, 8f 1x 2= x

-c

;c = 1, 3, 5, 7

SECTION 6.5

■

Power Functions: Negative Powers 535

33. Loudness of Sound The loudness L of a sound measured in decibels (dB) is

inversely proportional to the square of the distance d from the source of the sound.

(a) A person who is 10 ft from a lawn mower experiences a sound level of 70 dB. Find

the constant of proportionality, and write the equation that expresses the inverse

proportionality.

(b) How loud is the lawn mower when the person is 100 ft away?

34. Electrical Resistance The resistance R of a wire of a fixed length is inversely

proportional to the square of its diameter.

(a) A wire that is 1.2 meters long and 0.005 meter in diameter has a resistance of

140 ohms. Find the constant of proportionality, and write the equation that

expresses the inverse proportionality.

(b) Find the resistance of a wire made of the same material and of the same length as

the wire in part (a) but with a diameter of 0.008 meter.

35. Growing Cabbages In the short growing season of the Canadian arctic territory of

Nunavut, some gardeners find it possible to grow gigantic cabbages in the midnight sun.

Assume that the cabbages receive a constant amount of nutrients and that the final size

of a cabbage is inversely proportional to the number of other cabbages surrounding it.

(a) A cabbage that had 12 other cabbages around it grew to 30 pounds. Find the

constant of proportionality, and write the equation that expresses the inverse

proportionality.

(b) What size would this cabbage grow to if it had only 5 cabbage “neighbors”?

36. Newton’s Law of Gravitation The gravitational force between two objects is

inversely proportional to the square of the distance between them. How does the

gravitational force between two objects change if the distance between them is

(a) tripled? (b) halved?

37. Heat of Campfire The heat experienced by a hiker at a campfire is inversely

proportional to the cube of his distance from the fire.

(a) Write an equation that expresses the inverse proportionality.

(b) If the hiker is too cold and moves halfway closer to the fire, how much more heat

does the hiker experience?

38. Frequency of Vibration The frequency f of vibration of a violin string is inversely

proportional to its length L. The constant of proportionality k is positive and depends on

the tension and density of the string.

(a) Write an equation that represents this proportionality.

(b) What effect does doubling the length of the string have on the frequency of its

vibration?

536 CHAPTER 6

■

Power, Polynomial, and Rational Functions

■ Graphing Quotients of Linear Functions

A rational function is a function of the form , where p and q are

polynomial functions. We assume that the polynomials and q(x) have no fac-

tor in common. We first study rational functions that are quotients of two linear

functions:

To graph such a function, we can use “graphical division” as in Section 5.1. But

we’ll see that every such function is a transformation of the reciprocal function.

So to graph the function, we need to express it as an appropriate transformation

(shift or stretch) of the reciprocal function. The next example illustrates this

method.

y =

a + bx

c + dx

p 1x2

r 1x2= p 1x2>q1x 2

example

Graphing a Rational Function

Sketch a graph of each rational function.

(a) (b)

Solution

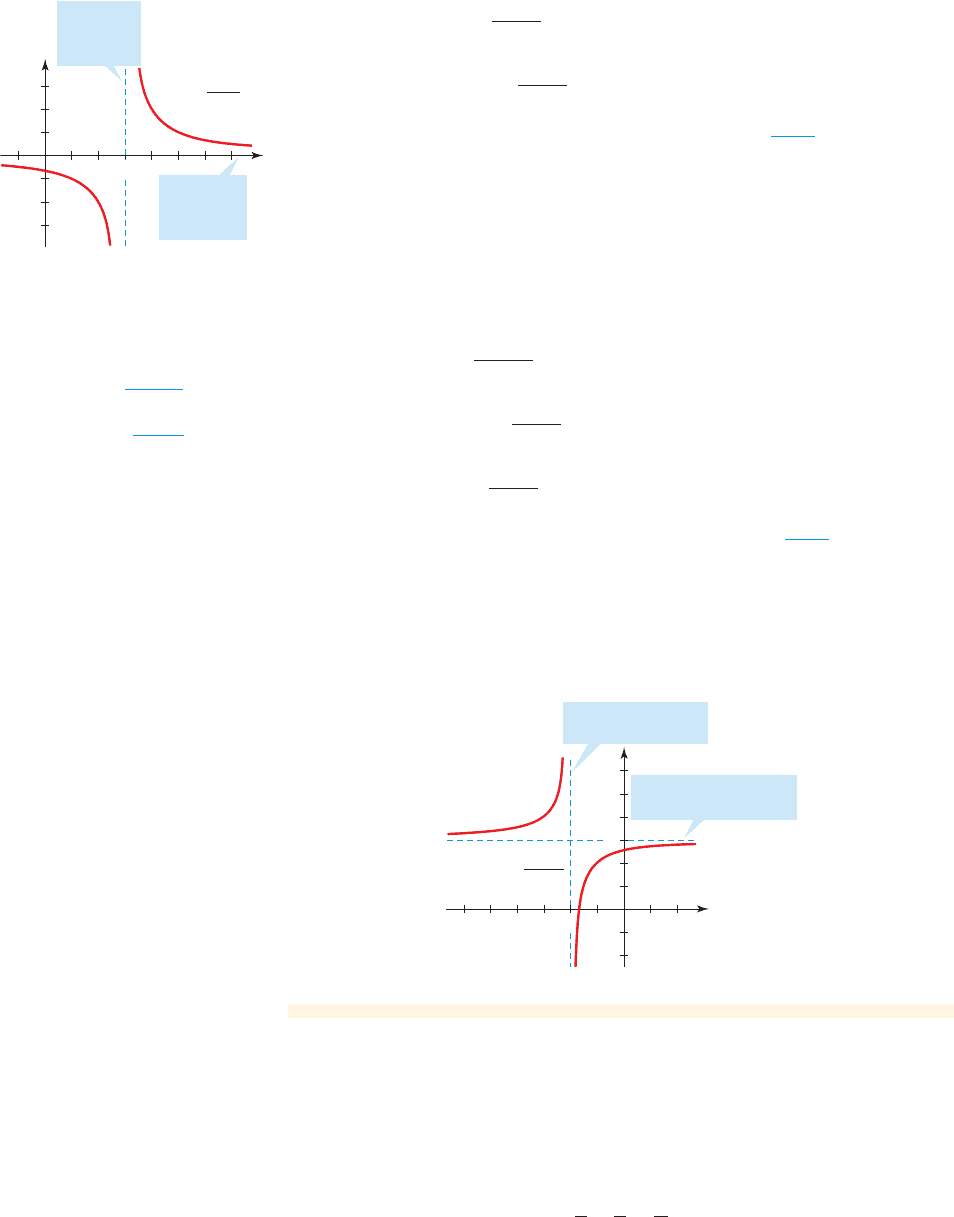
(a) Let . Then we can express r in terms of f as follows:f 1x2= 1>x

s1x 2=

3x + 5

x + 2

r1x 2=

x - 3

Focusing distance is a rational func-

tion of the focal length of a lens.

Lena Small/Shutterstock.com 2009

6.6 Rational Functions

■

Graphing Quotients of Linear Functions

■

Graphing Rational Functions

IN THIS SECTION… we study rational functions, which are quotients of polynomial

functions.

GET READY… by reviewing rational expressions and long division of polynomials in

Algebra Toolkit B.3. Check your understanding of these topics by doing the Algebra

Checkpoint at the end of this section.

We have encountered many real-world situations in which one quantity is directly or

inversely proportional to another. But the relationship between two quantities may

be more complicated, combining aspects of both direct and inverse dependence. In

many such cases the function relating the two quantities is a ratio of two polynomial

functions. Such functions are called rational functions.

For example, camera manufacturers use rational functions to model the rela-

tionship between the focusing distance and the focal length of a lens. Modern cam-

era lenses are really lens assemblies, made up of several individual lenses working

together. Combining such lenses makes it possible to manufacture telephoto lenses

that have adjustable focal lengths. The basic principle underlying the design of such

complex lenses is a rational function relating focal length and focusing distance

(see Example 2).

SECTION 6.6

■

Rational Functions 537

■ NOW TRY EXERCISES 29 AND 31 ■

Vertical

asymptote

x=3

Horizontal

asymptote

y=0

r(x)=

x-3

figure 1 Graph of

r1x 2= 2>1x - 32

Vertical asymptote

x=_2

Horizontal asymptote

y=3

s(x)=

x+2

3x+5

figure 2 Graph of

r 1x 2= 13x + 52>1x + 22

Division of polynomials is

reviewed in

Algebra Toolkit B.3

page T39.

- 1

3x + 6

x + 223x + 5

example

Focusing Distance for Camera Lenses

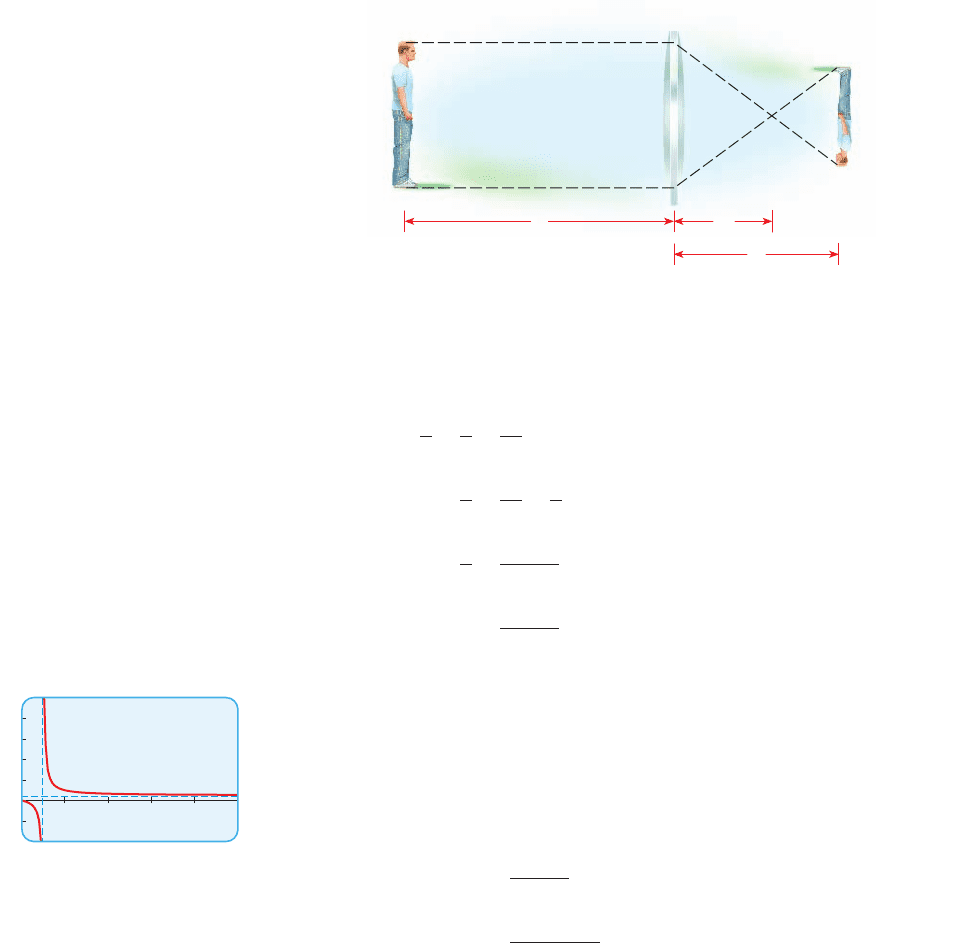
If a camera has a lens of fixed focal length F, then to focus on an object located a

distance x from the lens, the camera’s charge-coupled device (CCD) must be at a dis-

tance y behind the lens (see Figure 3), where F, x, and y are related by the equation

A CCD, or charge-coupled device,

is commonly used in the light sensor

of a digital camera.

Definition of r

Factor 2

Because

So the graph of r is obtained from the graph of f by shifting 3 units to the right

and stretching vertically by a factor of 2. Thus the graph of r has a vertical

asymptote and a horizontal asymptote . A graph of r is shown

in Figure 1.

(b) Let . Using long division (see the margin), we can express s in

terms of f as follows:

Definition of s

Long division (see margin)

Rearrange terms

Because

So the graph of s is obtained from the graph of f by shifting 2 units to the left,

reflecting in the x-axis, and then shifting upward 3 units. Thus s has vertical

asymptote and horizontal asymptote . The graph of s is shown

in Figure 2.

y = 3x =-2

f 1x + 22=

x + 2

=-f 1x + 2 2+ 3

x + 2

+ 3

= 3 -

x + 2

s1x 2=

3x + 5

x + 2

f 1x2= 1>x

y = 0x = 3

f 1x - 32=

x - 3

= 2f 1x - 32

= 2 a

x - 3

r 1x 2=

x - 3

538 CHAPTER 6

■

Power, Polynomial, and Rational Functions

This equation holds for x greater than F (otherwise no image is produced). Suppose

a camera has a 50-mm lens ( ).

(a) Express y as a function of x, and graph the resulting rational function.

(b) If a person is 3 m from the lens, what is the focusing distance?

the lens?

(d) What happens to the focusing distance y as the object moves closer to the lens?

F = 50

x F

figure 3

1000

_400

500

figure 4 Graph of

y = 50x>1x - 502

Solution

(a) We replace F by 50 in the equation and solve for y:

Replace F by 50

Subtract

Common denominator

Take the reciprocal of each side

The last equation defines y as a rational function of x. To graph this function, we

can use the methods of Example 1, but here we use a graphing calculator with

the viewing rectangle [0, 500] by . The graph is shown in Figure 4.

Note that the focusing distance y is never negative, so only the portion of the

graph to the right of the vertical asymptote applies to the problem.

(b) Since the person is 3 m from the lens, x is 3000 mm. Using this value of x, we

find the focusing distance y.

Focusing function

Replace x by 3000

Calculator

So the focusing distance is 50.85 mm.

L 50.85

3000

3000 - 50

y =

50x

x - 50

x = 50

3- 400, 10004

y =

50x

x - 50

50x

1>x

SECTION 6.6

■

Rational Functions 539

distance y approaches 50 as x becomes large.

(d) From the graph we see that as the distance x gets close to 50, the focusing

distance . (Of course, x cannot be less than 50.)

■ NOW TRY EXERCISE 41 ■

y Sq

y = 50

■ Graphing Rational Functions

The most important features of the graph of a rational function are its asymptotes. In fact,

once we locate all the asymptotes, we can readily complete the graph of a rational func-

tion. To find the asymptotes, we need to express the rational function in different ways.

In standard form, a rational function is expressed as the quotient of two polynomials

In factored form, the polynomials p and q are written in factored form. In the com-

pound fraction form, we divide numerator and denominator by the highest power

of x that appears in the polynomials p and q.

r 1x2=

p 1x2

q1x 2

example

Three Forms of a Rational Function

Express the rational function in factored form and in com-

pound fraction form.

Solution

In factored form, we factor the numerator and denominator. You can verify the fol-

lowing factorization:

Factored form

The highest power of x that appears in the numerator or denominator is . So to get

the compound fraction form, we divide numerator and denominator by .

Compound fraction form

■ NOW TRY EXERCISES 13 AND 23 ■

Each of the forms of a rational function helps us to discover a useful property of

the graph.

■

We use the standard form to find the y-intercept (by replacing x by 0).

■

We use the factored form to find the x-intercepts (these are the zeros of the

numerator) and the asymptotes (these are determined by the zeros of the

denominator).

r 1x2=

+ 7x - 4

+ x - 2

2 +

1 +

r 1x2=

+ 7x - 4

+ x - 2

12x - 1 21x + 4 2

1x - 1 21x + 2 2

r 1x2=

+ 7x - 4

+ x - 2

Rational expressions are

reviewed in

Algebra Toolkit B.3

page T39.

540 CHAPTER 6

■

Power, Polynomial, and Rational Functions

■

We use the compound fraction form to find the end behavior (by seeing

what happens as x gets large).

The procedure is explained in the next example.

example

Graphing a Rational Function

Consider the rational function .

(a) Find the x- and y-intercepts of the graph.

(b) Find the vertical asymptotes.

(d) Sketch a graph.

Solution

We use the three forms of this rational function found in Example 2.

(a) To find the y-intercept, we replace x by 0 in the standard form:

So the y-intercept is 2. To find the x-intercept, we replace y by 0 in the

factored form.

Replace y by 0 in factored form

The numerator is 0

Zero-Product Property

Solve

So the x-intercepts are and .

(b) The vertical asymptotes occur where the denominator is zero. The factored form is

The denominator is zero when x is 1 or . So the vertical asymptotes are the

vertical lines

large. Let’s write the compound fraction form and see what happens as x gets

large. In this case the fractions , and go to zero. So we have

So the graph gets closer to 2 as x gets large. This means that the horizontal

asymptote is the horizontal line .y = 2

y =

2 +

1 +

S 

2 + 0 + 0

1 + 0 + 0

= 2

2>x

7>x, 4>x

, 1>x

x = 1andx =-2

- 2

y =

12x - 1 21x + 4 2

1x - 1 21x + 2 2

- 4

x =



orx =-4

2 x - 1 = 0orx + 4 = 0

12x - 121x + 42= 0

12x - 121x + 42

1x - 121x + 22

= 0

y =

210 2

+ 710 2- 4

10 2

+ 102- 2

= 2

y =

+ 7x - 4

+ x - 2

SECTION 6.6

■

Rational Functions 541

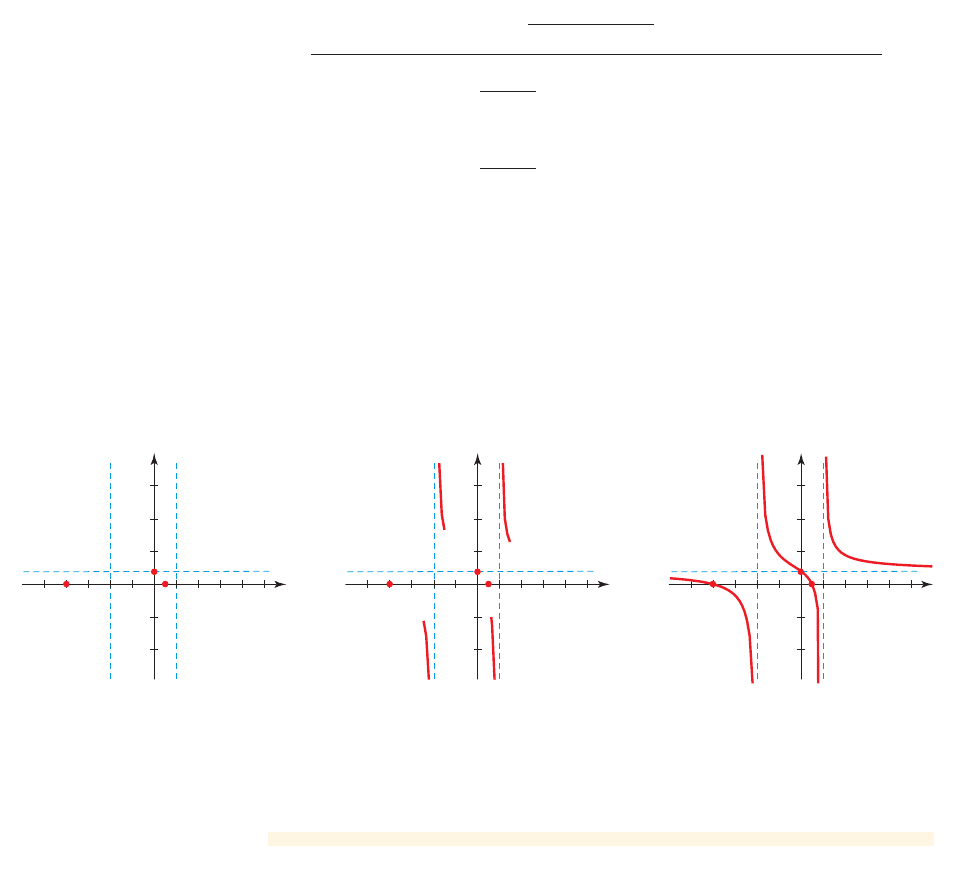
(d) We sketch the graph in three steps.

■

First we sketch the asymptotes and intercepts as shown in Figure 5(a).

■

Next, we examine the behavior of the graph near each vertical asymptote.

We choose test points to the left and right of each asymptote to help us

decide whether the graph goes up ( ) or down ( ) as x gets

near a vertical asymptote. For example, near the vertical asymptote

we choose the test points 0.9 and 1.1. From the factored form we can

quickly decide the sign of y at the test points by examining the sign of each

factor (as shown in the table below).

x = 1

y S

- qy Sq

The information in the table allows us to sketch the graph near the

asymptote as shown in Figure 5(b). A similar table allows us to

sketch the graph near the asymptote , also shown in Figure 5(b).

■

Finally, we complete the graph by connecting the parts already sketched,

making sure that we approach the horizontal asymptotes as x gets large in

the positive and negative directions. (See Figure 5(c).)

x =-2

x = 1

Test point

Sign of y ⴝ

12x ⴚ 121x ⴙ 42

1x ⴚ 121x ⴙ 22

Behavior near

asymptote

0.9

negative

1+ 21+ 2

1- 21+ 2

y S - qasx S 1

1.1

positive

1+ 21+ 2

y Sqasx S 1

■ NOW TRY EXERCISE 37 ■

(a) Asymptotes and intercepts (b) Behavior near asymptotes (c) Graph of function

figure 5

Steps in graphing

y = 12x

+ 7x - 42>1x

+ x - 22

542 CHAPTER 6

■

Power, Polynomial, and Rational Functions

Check your working knowledge of rational expressions and division of polyno-

mials by doing the following problems. You can review these topics in

Algebra

Toolkit B.3

on page T39.

1. Simplify the rational expression.

(a) (b) (c) (d)

2. Perform the indicated operations and simplify.

(a) (b) (c) (d)

3. Find the quotient and the remainder using long division.

(a) (b) (c) (d)

4. Find the quotient and the remainder using long division.

(a) (b)

- 8x + 2

x + 3

- 6x - 8

x - 4

2x - 5

x - 1

8x + 5

x - 2

x - 3

x + 1

3x + 5

x + 2

+ x

x + 1

x + 2

2 +

x + 3

x + 1

x - 1

- x

- 6x

- 7x + 6

+ 6x + 8

+ 5x + 4

x - 2

- 4

x + x

6.6 Exercises

Fundamentals

1. If the rational function has the vertical asymptote , then as ,

either

_______ or _______.

2. If the rational function has the horizontal asymptote , then

_______ as .

3. The rational function r is shown in standard form, factored form, and compound

fraction form. Identify each form of the function.

(a) :

_____________ form

(b) :

_____________ form

4. The following questions are about the rational function r in Exercise 3.

(a) The function r has x-intercepts

_______ and _______.

(b) The function r has y-intercept

_______.

(d) The function r has horizontal asymptote y ⫽

_______.

Think About It

5. Give an example of a rational function that has vertical asymptote . Now give an

example of one that has vertical asymptote and horizontal asymptote . Now

give an example of a rational function with vertical asymptotes and ,

horizontal asymptote , and x-intercept 4.y = 0

x =-1x = 1

y = 2x = 3

x = 3

x = _______ and x = _______.

r 1x 2=

- x - 2

- x - 6

r 1x 2=

1 -

r 1x 2=

1x + 121x - 2 2

1x + 221x - 3 2

x S;qy S

y = ay = r 1x2

y Sy S

x S a

x = ay = r 1x 2

CONCEPTS

SECTION 6.6

■

Rational Functions 543

SKILLS

6. Explain how you can tell (without graphing it) that the function

has no x-intercept and no vertical asymptote.

7–10

■ A rational function r is given.

(a) Complete each table for the function.

(b) Describe the behavior of the function near its vertical asymptote, based on Tables 1

and 2.

Tables 3 and 4.

r 1x 2=

+ 10

+ 15

r 1x 2

1.5

1.9

1.99

1.999

r 1x 2

2.5

2.1

2.01

2.001

r 1x 2

100

1000

r 1x 2

- 10

- 50

- 100

- 1000

table 1 table 2 table 3 table 4

7. 8. 9. 10.

11–14

■ Find the x- and y-intercepts of the rational function.

11. 12.

13. 14.

15–18

■ The graph of a rational function is given. Determine its x- and y-intercepts and its

vertical and horizontal asymptotes.

15. 16.

r 1x 2=

- 9

t1x 2=

- x - 2

x - 6

s1x 2=

x - 5

r 1x 2=

x - 1

x + 4

r 1x 2=

+ 1

1x - 22

r 1x 2=

3x - 10

1x - 22

r 1x 2=

4x + 1

x - 2

r 1x 2=

x - 2

17. 18.

−3

−4

−6