Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.


504 CHAPTER 6
■
Power, Polynomial, and Rational Functions
2
■ Polynomial Functions
A polynomial function is a function that is a sum of power functions. The following
are examples of polynomial functions:
Recall that the degree of a polynomial is the highest power of the variable that ap-
pears in the polynomial. So the degrees of the above polynomials are 3, 4, and 1, re-
spectively. In general, we have the following definition.
Polynomial Functions
f 1x2= 3x
3
+ 2x - 1g1x 2= x
4
+ 2x
3
h1x 2= 3x + 2
One way to graph a polynomial function is to graph the terms of the polynomial
(they are power functions), then use graphical addition.
A polynomial function is a function of the form
where are real numbers and n is a nonnegative integer.
■
If , then the polynomial has degree n.
■
The term is the leading term of the polynomial.a
n
x
n
a
n
⫽ 0
a
0
, a
1
, . . . , a
n
P1x 2= a
n
x
n
+ a
n -1
x
n -1
+
p
+ a
1
x + a
0
2
6.3 Polynomial Functions: Combining Power Functions
■
Polynomial Functions
■
Graphing Polynomial Functions by Factoring
■
End Behavior and the Leading Term
■
Modeling with Polynomial Functions
IN THIS SECTION… we study polynomial functions as sums of power functions. We
learn how to graph a polynomial function using factoring.
GET READY… by reviewing how to factor polynomial expressions in Algebra Toolkit
B.2. Test your understanding by doing the Algebra Checkpoint at the end of this section.
Polynomial functions are obtained by combining power functions using the al-
gebraic operations on functions we studied in Section 6.1. In this section we’ll
encounter an application of polynomial functions to the ordinary task of mailing
a package at the post office. The U.S. Postal Service has restrictions on the size
of packages that it will mail. The rule is: The length of the package plus the dis-
tance around the package must not exceed a specified number of inches. To find
out the dimensions of the largest box that the Postal Service will mail requires
using polynomial functions, as we’ll see in Example 6. But first we must learn
how to graph polynomial functions.
Polynomial functions
at the post office
pzAxe/Shutterstock.com 2009
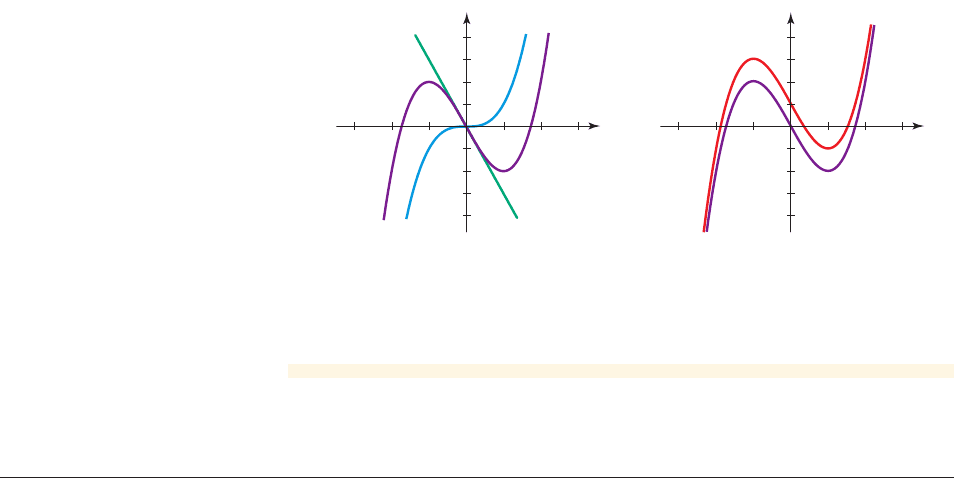
SECTION 6.3
■
Polynomial Functions: Combining Power Functions 505
example
1
Graphing a Polynomial with Graphical Addition
Graph the polynomial function by expressing it as a sum of
power functions and then using graphical addition.
Solution
The polynomial function f is the sum of the three power functions
We first graph and ; then we use graphical addition to graph their
sum , as in Figure 1(a). We now shift this graph up 1 unit to obtain the
graph of , as in Figure 1(b).y = x
3
- 3x + 1
y = x
3
- 3x
y =-3xy = x
3
y = x
3
y =-3xy = 1
f 1x2= x
3
- 3x + 1
1_3 2 3
x
y
_1
_2
_3
_4
2
3
4
(
a
)
Gra
p
h of
y
=x£-3x
y
=x£-3x
y=x£
y=_3x
1_1_3 2 3
x
y
_1
_2
_3
_4
2
3
4
(
b
)
Gra
p
h of
y
=x£-3x+1
y=x£-3x
y=x£-3x+1
figure 1 Graphing a polynomial function with graphical addition
■ NOW TRY EXERCISE 7 ■
2
■ Graphing Polynomial Functions by Factoring
If a polynomial function can be factored into linear factors, then an effective way to
graph the polynomial is to first use the zero-product property to find the x-intercepts.
Between consecutive x-intercepts the polynomial must be always positive or always
negative; to decide which sign is the correct one, we use test points. The process is
illustrated in the next example.
Intercepts are reviewed in
Algebra Toolkit D.2, page T71.
example
2
Graphing a Polynomial Function
Let .
(a) Show that .
(b) Find the x-intercepts of the graph of f.
(c) Find the sign of f on each of the intervals determined by the x-intercepts.
(d) Sketch a graph of f.
f 1x2= 1x - 321x + 221x - 22
f 1x2= x
3
- 3x
2
- 4x + 12
506 CHAPTER 6
■
Power, Polynomial, and Rational Functions
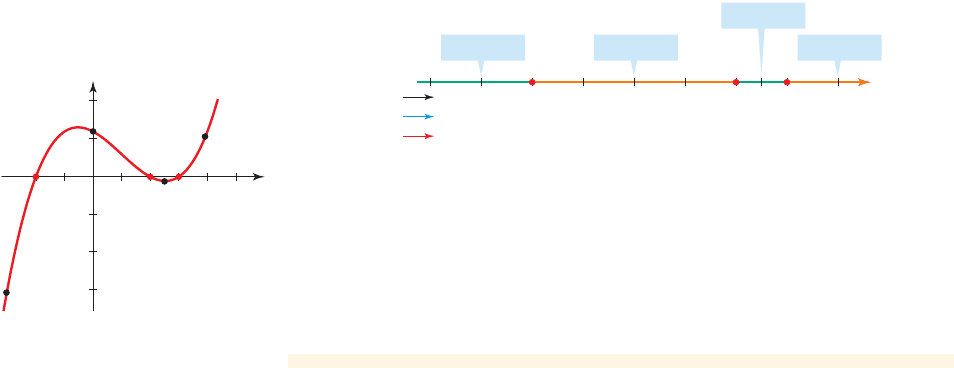
(d) We first plot the x-intercepts as well as the other points calculated in Figure 2.
The graph of f is above the x-axis on intervals where f is positive and below
the x-axis where f is negative. From Figure 2 we know the sign of f on each
interval, so we can complete the graph as in Figure 3.
■ NOW TRY EXERCISE 9 ■
Solution
(a) We expand the product to see whether it is the same expression as the expres-
sion defining f.
Sum and difference of terms
Distributive Property
Distributive Property
This last expression is the same as the expression defining f.
(b) The x-intercepts are the solutions to the equation . We have
Set equal to 0
Factored form
Zero-Product Property
Solve
So the x-intercepts are 3, , and 2.
(c) The x-intercepts separate the real line into four intervals (see Figure 2):
The function f is either positive or negative on each of these intervals. To
decide which it is, we pick a test point in the interval and evaluate f at that
point. For example, in the interval , let’s pick the test point .
Evaluating f at , we get
Factored form of f
Evaluate f at
Calculate
Since is less than 0, f is negative at each point in the entire interval
. In Figure 2 we choose test points in each of the four intervals and
determine the sign of the function f on each interval.
1- q, - 22
- 30
= 1- 621- 121- 52=-30
- 3 f 1- 32= 1- 3 - 321- 3 + 221- 3 - 2 2
f 1x 2= 1x - 3 21x + 221x - 22
- 3
- 31- q, - 22
1- q, - 22,1- 2, 22,12, 32,and13, q 2
- 2
x = 3 o r x =-2 o r x = 2
x - 3 = 0 orx + 2 = 0 orx - 2 = 0
1x - 321x + 221x - 22= 0
f 1x 2 x
3
- 3x
2
- 4x + 12 = 0
f 1x2= 0
= x
3
- 3x
2
- 4x + 12
= x
2
1x - 3 2- 41x - 32
1x - 321x + 221x - 22= 1x - 321x
2
- 42
It is usually easier to evaluate a
polynomial by using the factored
form. In Example 1 we used the
factored form to evaluate f at .- 3
432 2.50_2_3x
12_1.12512_30f(x)
+_+_Sign
Test point Test point Test point
Test point
figure 2 Intercepts and test points for f 1x 2= x
3
- 3x
2
- 4x + 12
y
x
0
1
10
figure 3 Graph of
f 1x 2= x
3
- 3x
2
- 4x + 12
SECTION 6.3
■
Polynomial Functions: Combining Power Functions 507
example
3
Graphing a Polynomial Function
Let .
(a) Express the function f in factored form.
(b) Find the x-intercepts of the graph of f.
(c) Find the sign of f on each of the intervals determined by the x-intercepts.
(d) Sketch a graph of f.
Solution
(a) We factor the polynomial completely.
Definition of f
Factor
Factor trinomial
(b) The x-intercepts are the solutions to the equation . We use the
factored form of f to solve this equation.
Set equal to 0
Zero-Product Property
Solve
So the x-intercepts are 0, , and 1.
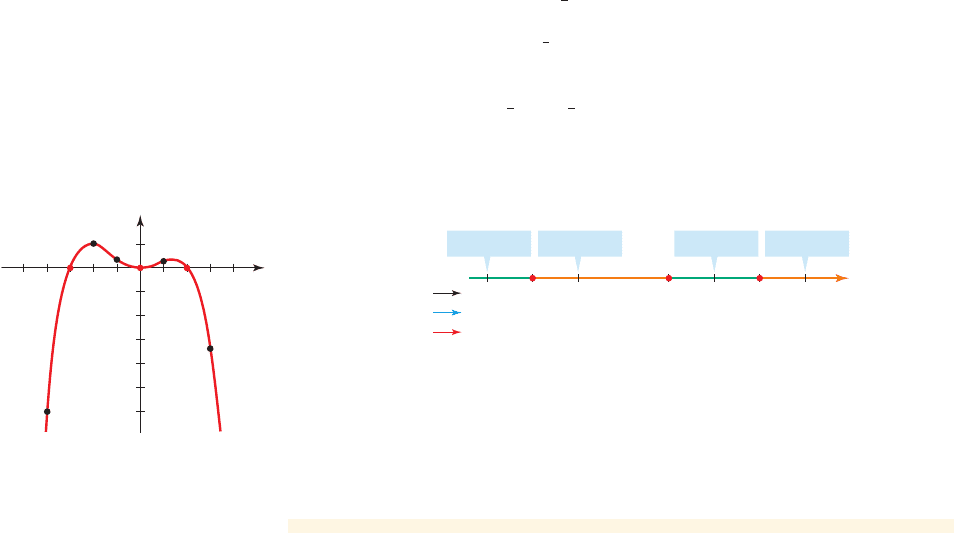
(c) The x-intercepts separate the real line into four intervals (see Figure 4):
To determine the sign of f on each of these intervals, we use test points as
shown in the diagram in Figure 4.
A- q, -
3
2
B,A-
3
2
, 0B,10, 1 2,and11, q 2
-
3
2
x = 0 or x =-
3
2
or x = 1
- x
2
= 0 or 2 x + 3 = 0 or x - 1 = 0
f 1x 2 - x
2
12x + 321x - 12= 0
f 1x2= 0
=-x
2
12x + 3 21x - 1 2
- x
2
=-x
2
12x
2
+ x - 32
f 1x 2=-2x
4
- x
3
+ 3x
2
f 1x2=-2x
4
- x
3
+ 3x
2
1.50.50_1.5 1_2 _1x
_6.750.5_12f(x)
_+_
2
+Sign
Test pointTest pointTest pointTest point
figure 4 Intercepts and test points for f 1x 2=-2x
4
- x
3
+ 3x
2
(d) We plot the x-intercepts as well as the test points that we calculated in the
diagram in Figure 4. The graph of f is above the x-axis on intervals where f is
positive and below the x-axis where f is negative, as shown in Figure 5.
■ NOW TRY EXERCISE 19 ■
y
x
0
1
2
_12
figure 5 Graph of
f 1x 2=-2x
4
- x
3
+ 3x
2
example
4
Graphing a Polynomial Function
Let .
(a) Express the function f in factored form.
(b) Find the x-intercepts of the graph of f.
f 1x2= x
3
- 2x
2
- 4x + 8
508 CHAPTER 6
■
Power, Polynomial, and Rational Functions
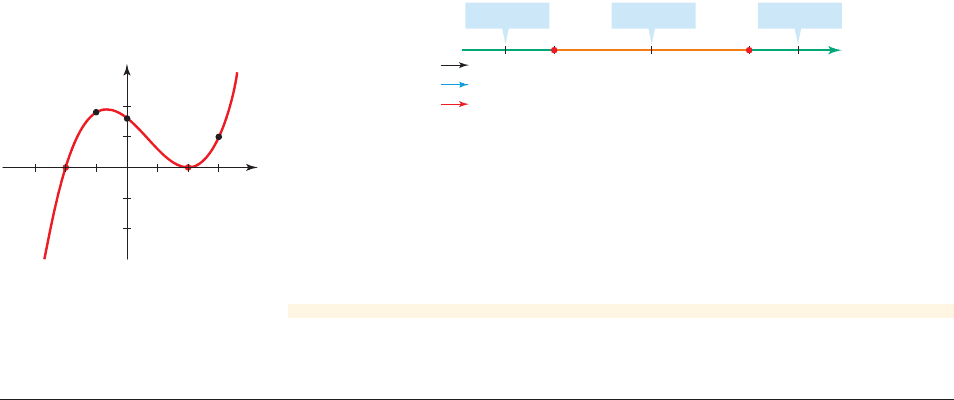
30_2 2_3x
58_25f(x)
++_Sign
Test pointTest pointTest point
figure 6 Intercepts and test points for
f 1x 2= x
3
- 2x
2
- 4x + 8
(c) Find the sign of f on each of the intervals determined by the x-intercepts.
(d) Sketch a graph of f.
Solution
(a) We factor the polynomial by grouping.
Definition of f
Group
Factor each term
Factor from each term
Factor difference of squares
(b) The x-intercepts are the solutions to the equation . We use the
factored form of f to solve this equation.
Set equal to 0
Zero-Product Property
Solve
So the x-intercepts are and 2.
(c) The x-intercepts separate the real line into three intervals (see Figure 6):
To determine the sign of f on each of these intervals, we use test points as
shown in the diagram in Figure 6.
1- q, - 22,
1- 2, 22,and12, q 2
- 2
x =-2 or x = 2 or x = 2
x + 2 = 0 or x - 2 = 0 or x - 2 = 0
f 1x 2 1x + 2 21x - 2 21x - 22= 0
f 1x2= 0
= 1x + 221x - 221x - 2 2
x - 2 = 1x
2
- 421x - 22
= x
2
1x - 2 2- 41x - 22
= 1x
3
- 2x
2
2+ 1- 4x + 8 2
f 1x 2= x
3
- 2x
2
- 4x + 8
(d) We plot the x-intercepts as well as the test points that we calculated in the
diagram in Figure 6. The graph of f is above the x-axis on intervals where f is
positive and below the x-axis where f is negative, as shown in Figure 7.
■ NOW TRY EXERCISE 23 ■
y
x
0
1
5
figure 7 Graph of
f 1x 2= x
3
- 2x
2
- 4x + 8
2
■ End Behavior and the Leading Term
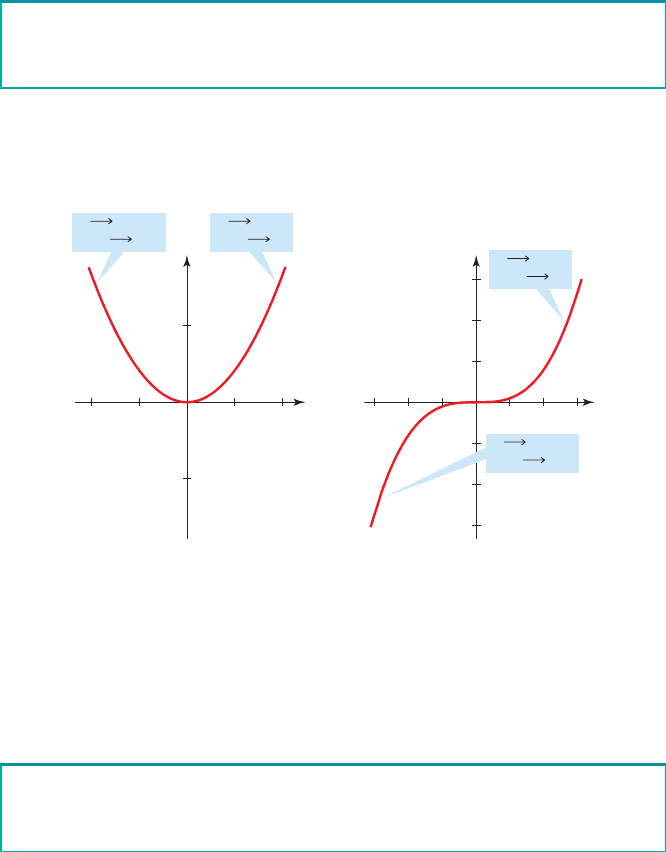
The end behavior of a polynomial function is a description of what happens to the
values of the function as x becomes large in the positive or negative direction. To ex-
plain end behavior, we use the following arrow notation.
SECTION 6.3
■
Polynomial Functions: Combining Power Functions 509
means “x becomes large in the positive direction”
means “x becomes large in the negative direction”x S
- q
x Sq
Arrow Notation
For example, the power functions and have the end behavior shown in
Figure 8.
y = x
3
y = x
2
y
y=x£
y=x™
x
0
10
20
30
_10
_20
_30
y
x
0
10
_10
_2_4 42_2_3 _1 213
y
as x _`
_`
y
as x _`
` y
as x `
`
y
as x `
`
figure 8 End behavior of and y = x
3
y = x
2
Power functions with even powers have end behavior like that of or
, and power functions with odd powers have end behavior like that of
or . But how do we determine the end behavior of any polynomial? For any
polynomial function the end behavior is completely determined by the leading term.
End Behavior
y =-x
3
y = x
3
y =-x
2
y = x
2
A polynomial function has the same end behavior as the power function
consisting of its leading term.
So the polynomial function has the
same end behavior as the power function . The reason is that for large
values of x the other terms are relatively insignificant in size when compared to the
leading term. The next example illustrates this relationship.
Q1x 2= a
n
x
n
P1x 2= a
n
x
n
+ a
n -1
x
n -1
+
p
+ a
1
x + a
0
example
5
Graphing a Polynomial Function
Let .
(a) Determine the end behavior of the leading term of P.
(b) Confirm that P and its leading term have the same end behavior by comparing
their values for large values of x.
P1x 2= 3x
5
- 5x
3
+ 2x

510 CHAPTER 6
■
Power, Polynomial, and Rational Functions
(c) Confirm that P and its leading term have the same end behavior by graphing
them together.
Solution
(a) The leading term of P is the function . Since Q is a power function
with odd power, its end behavior is as follows:
(b) We make a table of values of P and Q for large values of x. We see that when x
is large, P and Q have approximately the same value (in each case ).
This confirms that they have the same end behavior as .x Sq
y Sq
y Sq as x Sq
andy S - q as x S - q
Q1x 2= 3x
5
x
P1x 2ⴝ 3x
5
ⴚ 5x
3
ⴙ 2x Q1x2ⴝ 3x
5
15 2,261,280 2,278,125
30 72,765,060 72,900,000
50 936,875,100 937,500,000
(c) Figure 9 shows the graphs of P and Q in progressively larger viewing
rectangles. The larger the viewing rectangle, the more the graphs look alike.
This confirms that they have the same end behavior.
10,000
_10,000
_10 10
50
_50
_3 3
2
_2
_2 2
QP
1
_1
_1 1
Q
P
P
Q
P
Q
figure 9 Graphs of P and Q in progressively larger viewing rectangles
■ NOW TRY EXERCISE 27 ■
2
■ Modeling with Polynomial Functions
We have seen that the graphs of polynomial functions often have local maximum and
minimum values. In the applications of polynomials these points often play an im-
portant role, as we’ll see in the next example.
Local maxima and minima of
functions are studied in Section 1.7.
example
6
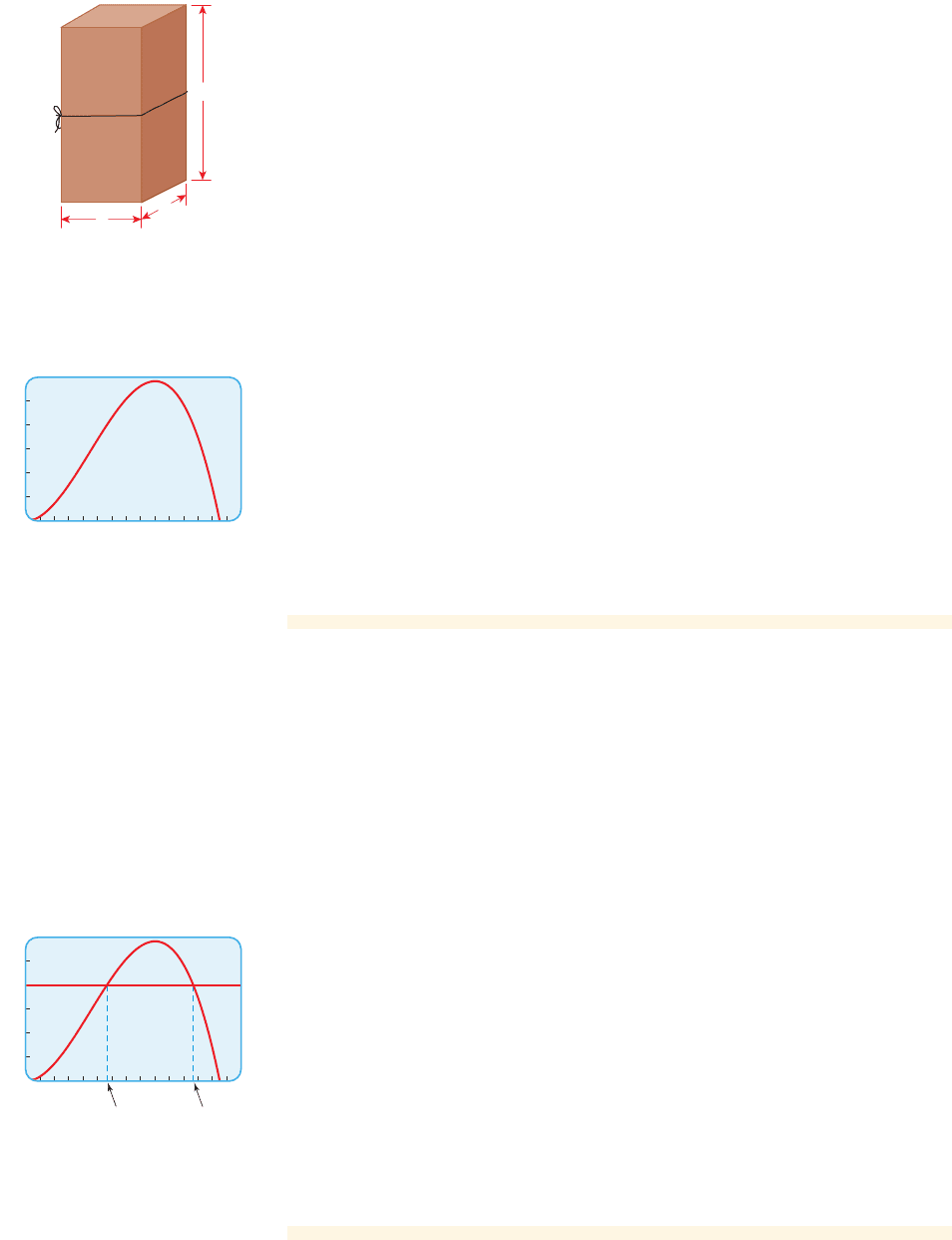
Finding Maximum Volume
Your local post office will mail a package only if its length plus girth is 108 inches
(or less). April wants to mail a package in the shape of a rectangular box with a
square base. To get the largest volume, she wants the length plus the girth to be ex-
actly 108 inches.
(a) Express the volume of the package as a function of the side x of the base.
(b) Use a graphing calculator to graph in the viewing rectangle [0, 30] by
[0, 12,000]. For what value of x does the maximum volume occur?
(c) What are the dimensions of the box with greatest volume that April can mail
at the post office?
V
V
SECTION 6.3
■
Polynomial Functions: Combining Power Functions 511
x
x
L
figure 10 Girth is the “distance
around.”
Solution
(a) Let x be the side of the base and let L be the length, as shown in Figure 10.
The volume of the box is
Volume of box
To express as a function of the variable x alone, we need to eliminate L. We
know that , so . Using this expression for L, we
can now express the function as a function of x alone.
Volume of box
Replace L by
Distributive property
(b) The graph is shown in Figure 11. From the graph we see that the maximum
value occurs when x is 18.
(c) To obtain the box with maximum volume, the side x of the base must be 18.
Let’s find the length of the box.
From part (a)
Replace x by 18
Calculate
So the dimensions of the box with maximum volume are
inches.
■ NOW TRY EXERCISE 47 ■
18 * 18 * 36
= 36
= 108 - 4
#
18
L = 108 - 4x
V = 108x
2
- 4x
3
108 - 4x V = x
2
1108 - 4x 2
V = x
2
L
V
L = 108 - 4x4x + L = 108
V
V = x
2
L
figure 11 Graph of
V = 108x
2
- 4x
3
0
30
12,000
example
7
Solving a Polynomial Equation Graphically
If the box in Example 6 is to have a volume of 8000 cubic inches, what are the di-
mensions of the box?
Solution
From Example 6 we know that the volume of the box is modeled by the function
We graph the function and the line in Figure 12. From
the graph we see that the volume is 8000 when x is approximately 11.28 or 23.32.
To find the corresponding lengths L, we use the equation , which we
found in Example 6.
For we have .
For we have .
So there are two possible boxes of the given shape having volume 8000 cubic inches.
Their dimensions are approximately
where all distances are measured in inches.
■ NOW TRY EXERCISE 49 ■
11.28 * 11.28 * 62.88or23.32 * 23.32 * 14.72
L L 108 - 4123.322= 14.72x L 23.32
L L 108 - 4111.282= 62.88x L 11.28
L = 108 - 4x
V = 8000V = 108x
2
- 4x
3
V = 108x
2
- 4x
3
0
30
12,000
11.28 23.32
figure 12

512 CHAPTER 6
■
Power, Polynomial, and Rational Functions
Fundamentals
1. (a) A polynomial function is a sum of _______ functions.
(b) The polynomial is the sum of the power functions
______, ______, and ______. The leading term of P is ______,
and the degree of P is
_______.
2. (a) To find the zeros of a polynomial function, we first
_______ the polynomial and
then apply the Zero-Product Property. The zeros of a polynomial are the
____-
intercepts of the graph of the polynomial.
(b) The polynomial function is in factored form.
The zeros of f are
____, ____, ____. The x-intercepts of the graph of f are ____,
____, ____.
3. Between consecutive x-intercepts the values of a polynomial must always be
_____________ or always be _____________. To decide which sign is the
appropriate one, we use
_______ points.
4. Every nonconstant polynomial has one of the following end behaviors:
(i)
(ii)
(iii)
(iv)
For each polynomial, choose the appropriate description of its end behavior from the
list above.
(a) ; end behavior:
__________________________.
(b) ; end behavior:
__________________________.
(c) ; end behavior:
__________________________.
(d) ; end behavior:
__________________________.y =-5x
6
- 3x
3
+ 9x + 12
y = 5x
6
+ 3x
3
- 9x - 12
y =-x
3
+ 8x
2
- 2x + 15
y = x
3
- 8x
2
+ 2x - 15
y S
- q as x Sq and y S - q as x S - q
y S
- q as x Sq and y Sq as x S - q
y Sq as x Sq and y S
- q as x S - q
y Sq as x Sq and y Sq as x S
- q
f 1x 2= 1x - 221x + 121x - 32
y =y =y =
P1x 2= 3x
4
- 2x
3
+ 4
Check your knowledge of factoring polynomial expressions by doing the follow-
ing problems. You can review these topics in
Algebra Toolkit B.2
on page T33.
1. Factor out the common factor.
(a) (b) (c) (d)
2. Factor the quadratic.
(a) (b) (c) (d)
3. Factor the expression completely.
(a) (b) (c) (d)
4. Factor the expression by grouping terms.
(a) (b)
7z
5
- 14z
3
+ 5z
2
- 10x
3
+ 3x
2
+ x + 3
r
6
- 12r
3
+ 36x
5
+ 3x
4
- 28x
3
w
4
- 163t
5
- 12t
3
3n
2
- n - 2t
2
+ 3t - 2825m
2
+ 10m + 1x
2
- 81
2y
3
- 6y
2
+ 4yt
4
+ 4t
2
r
2
- 3r6x
2
+ 3
CONCEPTS
6.3 Exercises

SECTION 6.3
■
Polynomial Functions: Combining Power Functions 513
Think About It
5. Can the polynomial whose graph is shown have a degree that is even?
y
x
0
6. A function f is odd if or even if .
(a) Explain why a power function that contains only odd powers of x is an odd function.
(b) Explain why a power function that contains only even powers of x is an even
function.
(c) Explain why a power function that contains both odd and even powers of x is
neither an odd nor an even function
7–8
■ Graph the given polynomial function by expressing it as a sum of power functions,
and then using graphical addition.
7. 8.
9. Let .
(a) Show that .
(b) Find the x-intercepts of the graph of f.
(c) Find the sign of f on each of the intervals determined by the x-intercepts.
(d) Sketch a graph of f.
10. Let .
(a) Show that .
(b) Find the x-intercepts of the graph of f.
(c) Find the sign of f on each of the intervals determined by the x-intercepts.
(d) Sketch a graph of f.
11–18
■ Sketch a graph of the polynomial function. Make sure your graph shows all
intercepts and exhibits the proper end behavior.
11. 12.
13. 14.
15. 16.
17. 18.
19–26
■ A polynomial function P is given.
(a) Express the function P in factored form.
(b) Sketch a graph of P.
19. 20.
21. 22.
23. 24.
25. 26. P1x 2= x
6
- 2x
3
+ 1P1x 2= x
4
- 3x
2
- 4
P1x 2= x
5
- 9x
3
P1x 2= x
4
- 3x
3
+ 2x
2
P1x 2=-2x
3
- x
2
+ xP1x 2=-x
3
+ x
2
+ 12x
P1x 2= x
3
+ 2x
2
- 8xP1x 2= x
3
- x
2
- 6x
P1x 2= 1x - 32
2
1x + 12
2
P1x 2= 1x - 12
2
1x - 32
P1x 2=
1
5
x1x - 52
2
P1x 2= 1x - 321x + 2213x - 22
P1x 2= 12x - 121x + 121x + 32P1x 2= x1x - 3 21x + 22
P1x 2= 1x - 121x + 121x - 22P1x 2= 1x - 121x + 22
f 1x 2= 1x + 321x - 221x +
22
f 1x 2= x
3
+ 3x
2
- 4x - 12
f 1x 2= 1x + 12
2
1x - 12
f 1x 2= x
3
+ x
2
- x - 1
f 1x 2= x
4
+ 2x - 1f 1x2=-x
3
+ 2x
2
+ 5
f 1- x2= f 1x2f 1- x2=-f 1x2
SKILLS
