Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

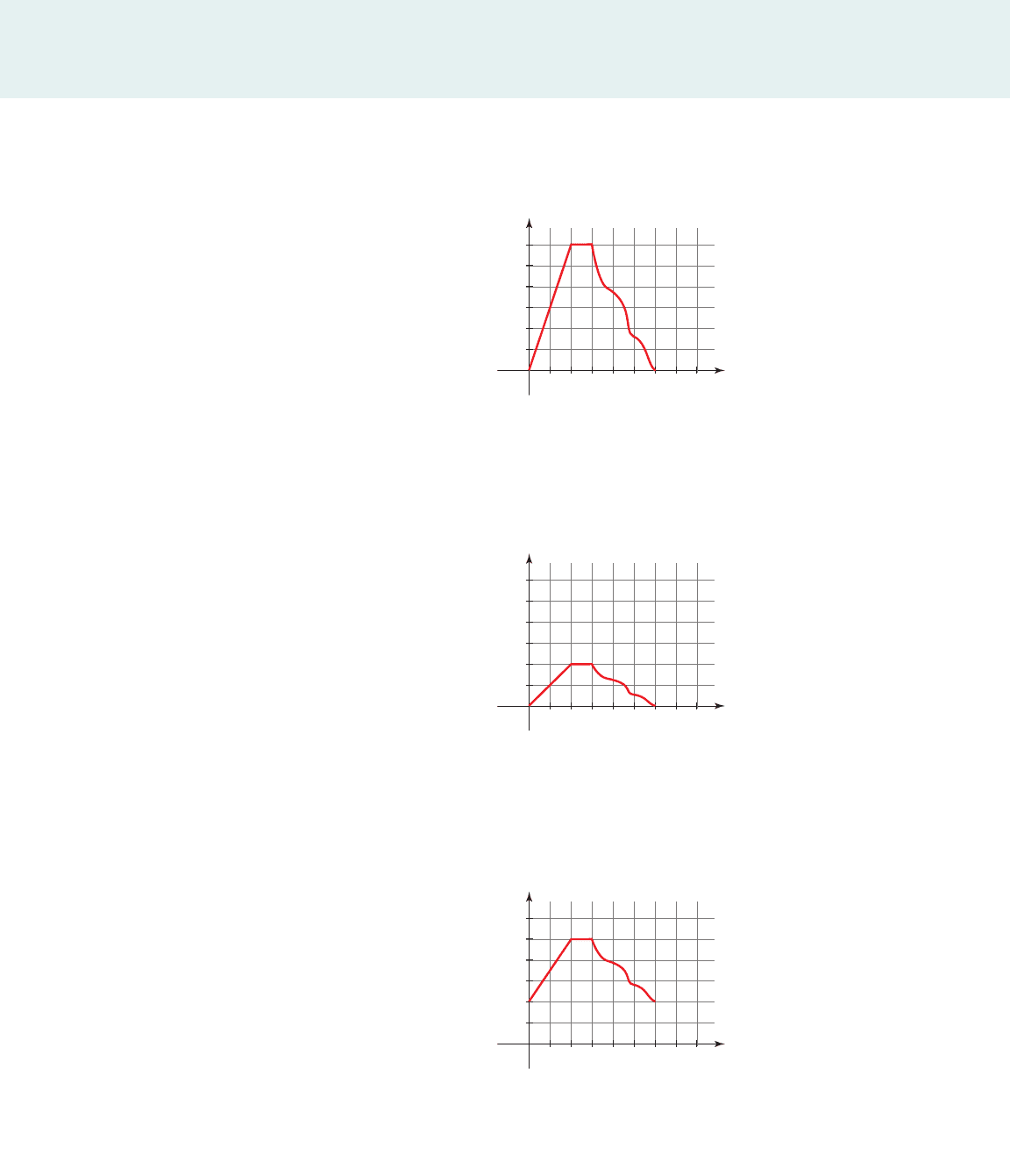
2. The graph gives Jerome’s distance from home at time t.B1t 2

Verbal: ____________________________________

Symbolic: ____________________________________

Story: ____________________________________

3. The graph gives Jerome’s distance from home at time t.C1t2

d (mi)

t (h)

12345678

100

120

d (mi)

t (h)

12345678

100

120

Verbal: ____________________________________

Symbolic: ____________________________________

Story: ____________________________________

d (mi)

t (h)

12345678

100

120

Verbal: ____________________________________

Symbolic: ____________________________________

Story: ____________________________________

4. The graph gives Jerome’s distance from home at time t.D1t 2

474 CHAPTER 5

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

5. The graph gives Jerome’s distance from home at time t.E1t 2

d (mi)

t (h)

12345678

100

120

Verbal: ____________________________________

Symbolic: ____________________________________

Story: ____________________________________

II. Making a Transformation Story

Let’s make up a story about Jerome’s trip by using transformations.

1. Make a graph and describe a story that corresponds to the verbal description

of a transformation of Jerome’s original trip:

d (mi)

t (h)

12345678

100

120

Verbal: ____________________________________

Symbolic: ____________________________________

Story: ____________________________________

2. Make up your own transformations and story about Jerome’s trip. Provide

verbal, symbolic, and graphical descriptions of the transformations you have

used, and then give a real-world description of the trip.

d (mi)

t (h)

12345678

100

120

Verbal: ____________________________________

Symbolic: ____________________________________

Story: ____________________________________

475

Shift 2 units to the right and two units up.

Torricelli’s Law

OBJECTIVE To obtain an expression for Torricelli’s Law by fitting a quadratic

function to data obtained from a simple experiment.

Evangelista Torricelli (1608–1647) was an Italian mathematician and scientist. He is

best known for his invention of the barometer. In Torricelli’s time it was known that

suction pumps were able to raise water to a limit of about 9 meters, and no higher.

The explanation at the time was that the vacuum in the pump could support the

weight of only so much water. In studying this problem, Torricelli thought of using

mercury, which is 14 times heavier than water, to test this theory. He made a one-

meter-long tube sealed at the top end, filled it with mercury, and set it vertically in a

bowl of mercury. The column of mercury fell to about 76 cm, leaving a vacuum at

the top of the tube. In an impressive leap of insight, Torricelli realized that the col-

umn of mercury is held up not by the vacuum at the top of the tube, but rather by the

air pressure outside the tube pressing down on the mercury in the bowl. He wrote:

I claim that the force which keeps the mercury from falling . . . comes from outside the

tube. On the surface of the mercury which is in the bowl rests the weight of a column

of fifty miles of air. Is it a surprise that . . . [the mercury] should rise in a column high

enough to make equilibrium with the weight of the external air which forces it up?

The device Torricelli made was the first barometer for measuring air pressure.

Another of Torricelli’s discoveries, based on the same principle but applied to

water pressure, is that the speed of a fluid through a hole at the bottom of a tank is

related to the height of the fluid in the tank. The precise relationship is known as

Torricelli’s Law.

I. Collecting the Data

In this exploration we use easily obtainable materials to conduct an experiment and

collect data on the speed of water leaking through a hole at the bottom of a cylindri-

cal tank. To do this, we measure the height of the water in the tank at different times.

You will need:

■

An empty 2-liter plastic soft-drink bottle

■

A method of drilling a small (4 mm) hole in the plastic bottle

■

Masking tape

■

A metric ruler or measuring tape

■

An empty bucket

Procedure:

This experiment is best done as a classroom demonstration or as a group project with

three students in each group: a timekeeper to call out seconds, a bottle keeper to es-

timate the height every 10 seconds, and a record keeper to record these values.

1. Drill a 4 mm hole near the bottom of the cylindrical part of a 2-liter plastic

soft-drink bottle. Attach a strip of masking tape marked in centimeters from 0

to 10, with 0 corresponding to the top of the hole.

2. With one finger over the hole, fill the bottle with water to the 10-cm mark.

Place the bottle over the bucket.

Evangelista Torricelli

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

Richard Le Borne

476 CHAPTER 5

3. Take your finger off the hole to allow the water to leak into the bucket. Record

the values of height of the water for seconds.

II. Testing the Theory

Torricelli’s Law states that when a fluid leaks through a hole at the bottom of a cylin-

drical tank, the height h of fluid in the tank is related to the time t the fluid has been

leaking by a quadratic function:

where the coefficients a, b, and c depend on the type of fluid, the radii of the cylin-

der and the hole, and the initial height of the fluid.

1. Use a graphing calculator to find the quadratic function that best fits the data.

2. Graph the function you found together with a scatter plot of the data in the

same viewing rectangle. Does the graph appear to fit the data well?

III. Another Method

Torricelli’s Law actually gives more information about the form of the quadratic

function model. It can be shown that the function defining the height of the fluid can

be expressed as

where the coefficients C and k depend on the type of fluid, the radii of the cylinder

and the hole, and the initial height of the fluid.

1. Let’s find C and k for the experiment we conducted in Part I.

(a) Use the fact that the height of the water is 10 cm when the time t is 0

to solve for C in the above equation.

(b) Use the height you obtained in the experiment when the time t is 60

seconds and the value of C you obtained in part (a) to solve for k in the

above equation.

2. Expand the expression for that you obtained in 1(c).

How does this model compare with the model you got in Part II?

h1t 2=

ⵧ

t +

ⵧ

h1t 2

h1t 2= 1

ⵧ

h1t 2

k = ________

h1t 2

C = ________

h1t 2

h1t 2= 1C - kt2

h1t 2=

ⵧ

t +

ⵧ

h1t 2= at

+ bt + c

t = 10, 20, 30, 40, 50, and 60h1t2

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

Time (s) Height (cm)

EXPLORATIONS 477

Quadratic Patterns

OBJECTIVE To recognize quadratic data and find quadratic functions that fit the

data exactly.

In Exploration 2 of Chapter 2 (page 233) we discussed the importance of finding pat-

terns, and we found many linear patterns. In Exploration 2 of Chapter 3 (page 315)

we found exponential patterns. In this exploration we find quadratic patterns. We’ve

already seen how quadratic functions model many real-world phenomena. But quad-

ratic patterns also occur in unexpected places, such as in cutting a pizza, as we’ll see

in this exploration.

I. Recognizing Quadratic Data

In this exploration we assume that the inputs are the equally spaced numbers

We want to find properties of the outputs that guarantee that there is a quadratic func-

tion that exactly models the data. So let’s consider the quadratic function

We find the first differences of the outputs and the second differences—that is, the

differences of the first differences. In the next question you are asked to perform the

calculations that confirm the entries in the following table. In particular, the second

differences are constant.

f 1x2= ax

+ bx + c

0, 1, 2, 3, p

1. For the quadratic function , let’s consider the inputs 0, 1,

2, 3, . . .

(a) Find the outputs corresponding to the inputs 0, 1, 2, 3, . . . .

_______ , _______ , _______ , _______

(b) Use your answers to part (a) to find the first differences:

_______ , _______ , _______

(d) Do your answers to parts (a)–(c) match the entries in Table 1?

f 132- f 122=f 122- f 112=f 112- f 102=

f 132=f 122=f 112=f 102=

f 1x2= ax

+ bx + c

x 0 1 2 3 4

f 1x 2

a + b + c 4b + 2b + c 9b + 3b + c 16b + 4b + c

First difference —

a + b 3a + b 5a + b 7a + b

Second difference — — 2a 2a 2a

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

table 1

Second differences for f 1x 2= ax

+ bx + c

478 CHAPTER 5

a + b

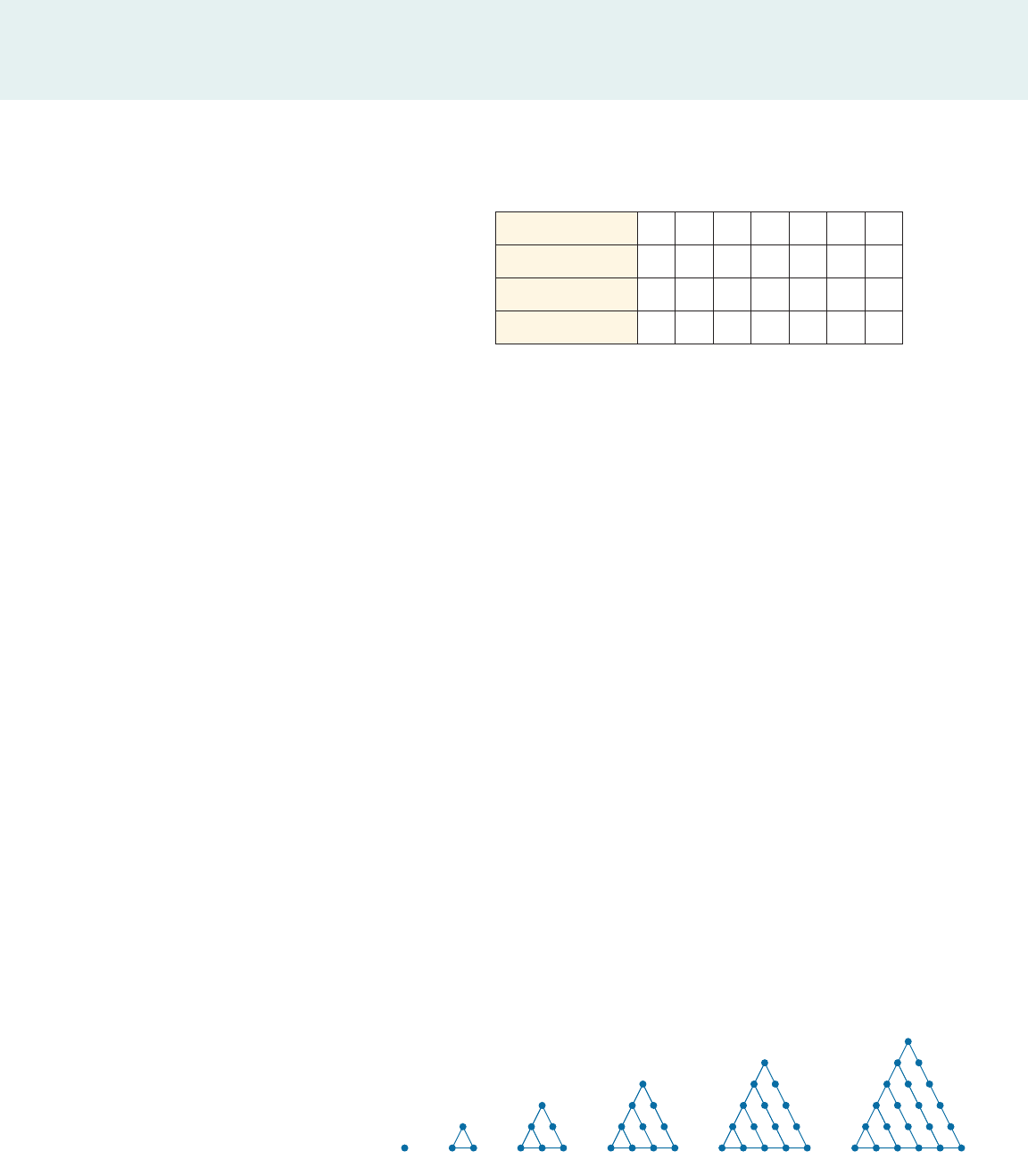
2. A data set is given in the table.

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

(a) Fill in the entries for the first and second differences.

(b) Observe that the second differences are constant, so there is a quadratic

function

that models the data. To find a, b, and c, let’s compare the entries in this

table to those in Table 1. Comparing the output corresponding to the input

0 in each of these tables, we conclude that

c  _____________

Comparing the second differences in each of these tables, we conclude

that

2a  _____________

Comparing the first differences in each of these tables, we conclude that

a  b  _____________

So a  _______ , b  _______ , and c  _______ .

(d) Check that the function f you found in part (b) matches the data. That is,

check that match the y-values in the data.

II. The Triangular Numbers

Many real-world situations have quadratic patterns. Here, we experiment with the

triangular numbers. The triangular numbers are the numbers obtained by placing

dots in a triangular shape as shown.

f 102, f 112, f 122, . . .

f 1x2= ____x

+ ____x + ____

f 1x2= ax

+ bx + c

x 0 1 2 3 4 5 6

y 5 10 19 32 49 70 95

First difference —

Second difference — —

121151063

EXPLORATIONS 479

1. Let’s find a formula for the nth triangular number.

(a) Complete the table for the first and second differences of the triangular

numbers

n 0 1 2 3 4 5

Triangular number f 1n2

1 3 6 10 15 21

First difference —

Second difference — —

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

(b) Observe that the second differences are constant, so there is a quadratic

function

that models the data. Find a, b, and c by comparing the entries in the table

in part (a) to those in Table 1. Comparing the output corresponding to the

input 0 in each of these tables, we conclude that

c  ____________

Comparing the second differences in each of these tables, we conclude

that

2a  ____________

Comparing the first differences in each of these tables, we conclude that

a  b  ____________

So _______ , _______ , and _______ .

Check that the function f models the data exactly. That is, check that

, . . . are the first, second, third, . . . triangular numbers.

(d) Use the model you found in part (c) to find the 100th triangular number

(when n is 100).

f 102, f 112, f 122

f 1n2= ____n

+ ____n + ____

c =b =a =

f 1n2= an

+ bn + c

480 CHAPTER 5

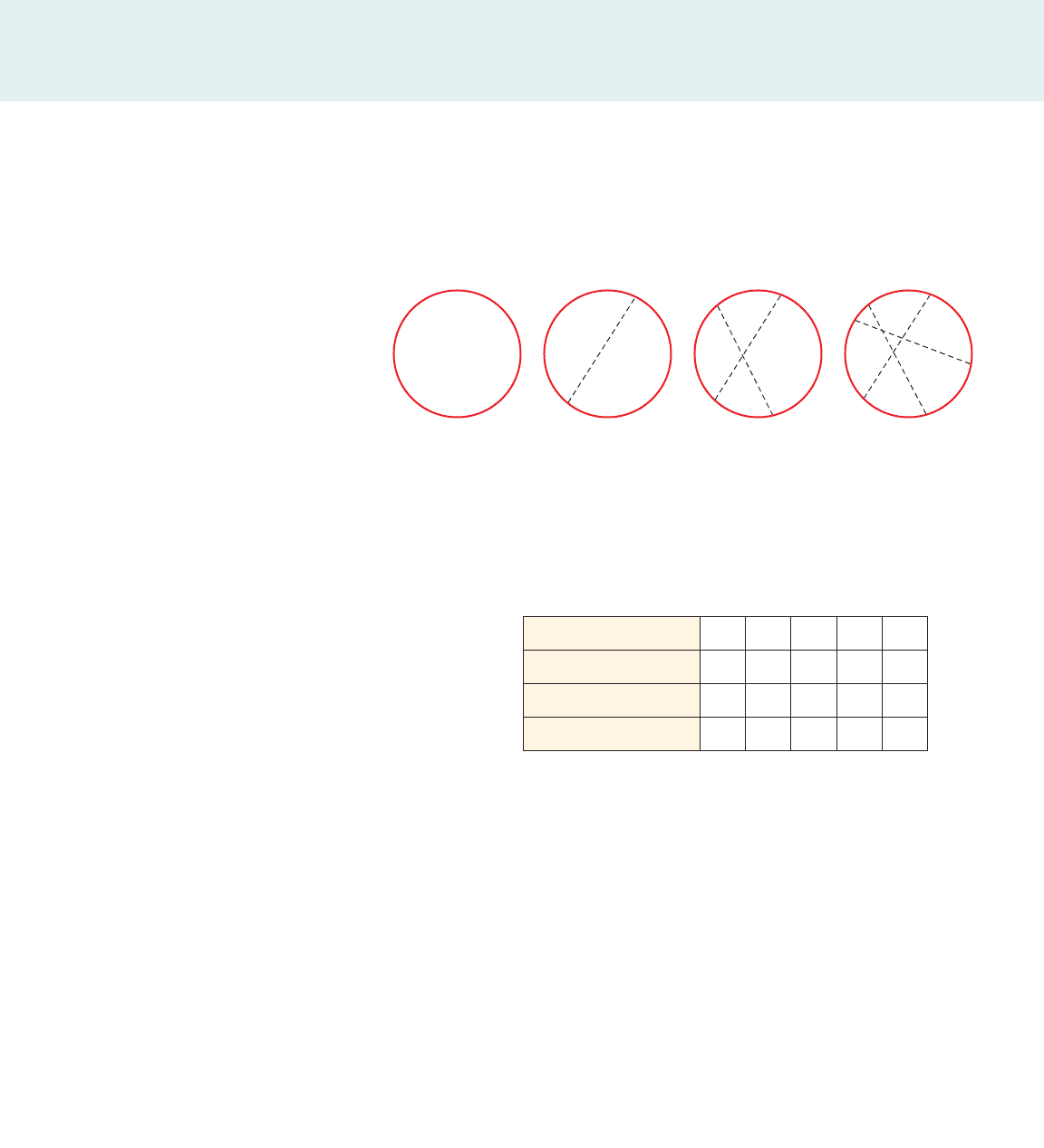
III. Cutting a Pizza

Let’s cut up a pizza—but not in the usual way. We want to cut the pizza in such a way

that we get the maximum possible number of pieces after each cut. The diagram

shows the number of pieces we can get by making 0, 1, 2, and 3 cuts.

1 2 4 7

Number of cuts n 0 1 2 3 4

Number of pieces f 1n 2

1 2 4 7 11

First difference —

Second difference — —

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

1. Let’s find a formula for the maximum number of pieces of pizza we can get by

making n cuts.

(a) Show that by making one more cut we can get 11 pieces of pizza.

(b) Complete the table for the first and second differences for the number of

pieces of pizza.

function

that models the data. Find a, b, and c by comparing the entries in the table

in part (b) to those in Table 1.

(d) A quadratic function that models the data is

Check that the function f models the data exactly. That is, check that

, . . . give the number of pizza pieces if we make 1, 2, 3, . . .

cuts.

(e) Use the model you found in part (d) to find the number of pieces of pizza

obtained by making 100 cuts.

f 102, f 112, f 122

f 1n2= ____n

+ ____n + ____

a = ________,b = ________,c = ________

f 1n2= an

+ bn + c

EXPLORATIONS 481

This page intentionally left blank

483

Only in the movies? Movies have some pretty fantastic creatures. Giant

apes as tall as skyscrapers, planet-sized spaceships, and a 50-foot-tall woman

(yes, there is such a movie: “Attack of the 50 Ft. Woman,” starring Daryl

Hannah in the 1993 remake of the 1958 cult classic). These creatures are so

large that they dwarf even giant prehistoric dinosaurs. Can such gargantuan

creatures actually exist? Should we fear that someday a real-life King Kong

might attack our towns? To answer such questions, we need to understand the

relationship between shape and size. Shape and size (length, area, and volume)

are related to each other by power functions, the main topic of this chapter.

We’ll see how power functions allow us to calculate the weight of a 500-foot

ape without having to actually meet one (see Exploration 1, page 554).

6.1 Working with Functions:

Algebraic Operations

6.2 Power Functions:

Positive Powers

6.3 Polynomial Functions:

Combining Power Functions

6.4 Fitting Power and Polynomial

Curves to Data

6.5 Power Functions:

Negative Powers

6.6 Rational Functions

EXPLORATIONS

Only in the Movies?

2 Proportionality:

Shape and Size

3 Managing Traffic

4 Alcohol and the Surge

Functions

Power, Polynomial,

and Rational Functions

Hulton Archive/Getty Images