Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

464 CHAPTER 5

■

Quadratic Functions and Models

5.5 Exercises

CONCEPTS

Fundamentals

1. When modeling data we make a _____________ plot to help us visually determine

whether a line or some other curve is appropriate for modeling the data.

2. If the y-values of a set of data increase and then decrease, then a _____________

function may be appropriate to model the data.

Think About It

3–4 ■ The following data are obtained from the function .f 1x 2= 1x - 32

x 0.1 0.8 0.8 1.2 1.7 2.3 2.6 3.1 3.3 3.4 3.9 4.1 5.2 5.9

y 101.2 106.7 105.2 110.1 112.7 114.6 113.3 113.1 109.1 110.4 109.2 107.1 97.6 95.5

x 0.2 0.3 0.9 1.4 1.5 1.8 2.4 2.6 3.9 4.1 4.7 5.2 5.5 6.3

y 37.8 41.7 45.8 46.2 48.1 49.9 47.3 45.1 42.4 36.2 32.5 29.3 27.9 21.8

x 0 1 2 3 4 5 6 7 8

f 1x 2

9 4 1 0 1 4 9 16 25

3. If you use your calculator to find the quadratic function that best fits the data, what

function would you expect to get? Try it.

4. Find the line of best fit for this data. Graph the line and a scatter plot of the data on the

same screen. How well does “the line of best fit” fit the data?

5–8

■ A set of data is given.

(a) Make a scatter plot of the data. Is it appropriate to model the data by a quadratic

function?

(b) Use a graphing calculator to find the quadratic model that best fits the data. Draw a

graph of the model.

SKILLS

x 0.5 0.7 1.3 1.9 2.3 2.8 2.9 3.3 3.7 4.1 4.1 4.4 4.9 5.5

y 52.1 48.2 45.3 40.8 39.7 35.5 34.1 32.5 31.2 32.7 33.4 36.1 38.3 41.2

x 0.0 0.2 0.7 1.2 1.2 2.1 2.9 3.1 3.5 3.7 4.2 4.3 5.5 6.1

y 13.1 12.2 10.1 9.2 9.6 8.7 8.6 9.1 10.7 10.9 11.8 13.4 16.9 18.2

SECTION 5.5

■

Fitting Quadratic Curves to Data 465

10. Too Many Corn Plants per Acre? The more corn a farmer plants per acre, the greater

is the yield the farmer can expect—but only up to a point. Too many plants per acre can

cause overcrowding and decrease yields. The data give crop yields per acre for various

densities of corn plantings, as found by researchers at a university test farm.

(a) Use a graphing calculator to find the quadratic model that best fits the data.

(b) Draw a graph of the model you found together with a scatter plot of the data.

9. Rainfall and Crop Yield Rain is essential for crops to grow, but too much rain can

diminish crop yields. The data give rainfall and cotton yield per acre for several seasons

in a certain county.

(a) Make a scatter plot of the data. Does a quadratic function seem appropriate for

modeling the data?

(b) Use a graphing calculator to find the quadratic model that best fits the data. Draw a

graph of the model.

CONTEXTS

Season Rainfall (in.) Yield (kg/acre)

1 23.3 5311

2 20.1 4382

3 18.1 3950

4 12.5 3137

5 30.9 5113

6 33.6 4814

7 35.8 3540

8 15.5 3850

9 27.6 5071

10 34.5 3881

Ted Wood/Getty Images

Density

(plants/acre)

Crop yield

(bushels/acre)

15,000 43

20,000 98

25,000 118

30,000 140

35,000 142

40,000 122

45,000 93

50,000 67

11. Height of a Baseball A baseball is thrown upward, and its height is measured at

0.5-second intervals using a strobe light. The resulting data are given in the table.

(a) Make a scatter plot of the data. Does a quadratic function seem appropriate for

modeling the data?

(b) Use a graphing calculator to find the quadratic model that best fits the data. Draw a

graph of the model on the scatter plot of the data.

(d) What is the maximum height attained by the ball?

Time (s) Height (m)

0.0 1.28

0.5 7.96

1.0 12.22

1.5 14.02

2.0 13.38

2.5 10.27

3.0 4.82

466 CHAPTER 5

■

Quadratic Functions and Models

12. Torricelli’s Law Water in a tank will flow out of a small hole in the bottom faster

when the tank is nearly full than when it is nearly empty. According to Torricelli’s Law,

the height of water remaining at time t is a quadratic function of t. A certain tank is

filled with water and allowed to drain. The height of the water is measured at different

times as shown in the table.

(a) Use a graphing calculator to find the quadratic model that best fits the data.

(b) Draw a graph of the model, together with a scatter plot of the data.

completely.

h1t 2

Time (min) Height (ft)

0 5.0

4 3.1

8 1.9

12 0.8

16 0.2

CHAPTER 5 REVIEW

CONCEPT CHECK

Make sure you understand each of the ideas and concepts that you learned in this chapter,

as detailed below section by section. If you need to review any of these ideas, reread the

appropriate section, paying special attention to the examples.

5.1 Working with Functions: Shifting and Stretching

Shifting Graphs Up and Down If , then:

■

To graph , shift the graph of upward by c units.

■

To graph , shift the graph of downward by c units.

Shifting Graphs Left and Right If , then:

■

To graph , shift the graph of to the left by c units.

■

To graph , shift the graph of to the right by c units.

Stretching and Shrinking Graphs Vertically To graph :

■

If , stretch the graph of vertically by a factor of c.

■

If , shrink the graph of vertically by a factor of c.

Reflecting Graphs

■

To graph , reflect the graph of in the x-axis.

■

To graph , reflect the graph of in the y-axis.

5.2 Quadratic Functions and Their Graphs

A squaring function is a function of the form , where .

A quadratic function is a function that has been derived from a squaring func-

tion by applying one or more of the transformations described in Section 5.1.

Every quadratic function can be described in either of the following forms:

■

General form: , where

■

Standard form: , where a  0f 1x 2= a1x - h 2

+ k

a  0f 1x 2= ax

+ bx + c

C  0f 1x 2= Cx

y = f 1x2y = f 1- x2

y = f 1x2y =-f 1x 2

y = f 1x20 6 c 6 1

y = f 1x2c 7 1

y = cf 1x2

y = f 1x2y = f 1x - c 2

y = f 1x2y = f 1x + c 2

c 7 0

y = f 1x2y = f 1x 2- c

y = f 1x2y = f 1x 2+ c

c 7 0

CHAPTER 5

■

Review 467

A quadratic function written in general form can be expressed in standard form by

completing the square.

The graph of a quadratic function is most easily obtained from the standard

form. The graph of is a parabola with vertex (h, k); it opens

upward if and downward if .a 6 0a 7 0

f 1x2= a1x - h 2

+ k

Ï=a(x-h)™+k, a>0

Ï=a(x-h)™+k, a<0

Vertex (h, k)

5.3 Maxima and Minima: Getting Information from a Model

If a quadratic function is given in standard form , then we have

the following:

■

If , then f has the minimum value at the vertex of its graph.

■

If , then f has the maximum value at the vertex of its graph.

If a quadratic function is given in general form , then its mini-

mum or maximum value occurs at .

■

If , then f has the minimum value .

■

If , then f has the maximum value .

5.4 Quadratic Equations: Getting Information from a Model

To get information from a quadratic model, we often need to solve a quadratic

equation, which is an equation of the form

To solve a quadratic equation, we use one of the two following methods:

■

Factoring: If the left-hand side of the equation factors readily, factor it, set

each factor equal to zero, and solve the resulting simpler equations.

■

Quadratic formula: If factoring is not practical, use the Quadratic Formula

The discriminant D of a quadratic equation is the number that appears inside the

square root in the quadratic formula, that is, .

■

If , then the equation has two distinct real solutions.

■

If , then the equation has exactly one real solution.

■

If , then the equation has no real solutions.D 6 0

D = 0

D 7 0

D = b

- 4ac

x =

- b ; 2b

- 4ac

+ bx + c = 0

f 1- b>12a22a 6 0

f 1- b>12a22a 7 0

x =-b>12a2

f 1x2= ax

+ bx + c

f 1h2= ka 6 0

f 1h2= ka 7 0

f 1x2= a1x - h 2

+ k

468 CHAPTER 5

■

Quadratic Functions and Models

REVIEW EXERCISES

1–6 ■ Sketch the graph of f. Then use shifting, stretching, and/or reflecting to sketch the

graph of on the same axes.

1. 2.

3. 4.

5. 6.

7–10

■ Sketch the graph of the function, not by plotting points, but by starting with the

graph of a basic function and applying transformations.

7. 8.

9. 10.

11–12

■ A quadratic function is given.

(a) Express the function in general form.

(b) Express the function in standard form.

11. 12.

13–18

■ A quadratic function in general form is given.

(a) Express the function in standard form.

(b) What is the vertex of the graph of the function?

(d) Find the average rate of change of the function between and .

13. 14.

15. 16.

17. 18.

19–20

■ Find an equation for the parabola with the given properties.

19. The vertex is and the y-intercept is 3.

20. The vertex is and it passes through the point (1, 4).13, - 42

1- 2, 62

f 1x 2=-2x

+ 6x + 7f 1x 2=

- x - 3

f 1x 2= x

- 3x +

f 1x 2=-x

+ 4x + 5

f 1x 2=-x

+ 4xf 1x 2= x

+ 6x

x = 3x = 1

g1x 2= 1x - 321x - 12- 8f 1x 2= 1x + 421x - 22

k1x 2=-2 1x + 9

+ 1h1x 2= 31x - 2 + 1

g1x 2= 1x - 22

- 4f 1x 2=-1x + 32

f 1x 2= 1x,g1x 2= 21x + 4f 1x 2= x

,g1x 2=-1x - 12

+ 4

f 1x 2= log x,

g1x 2= log1x - 3 2f 1x2= 1x,g1x2= 1x + 9

f 1x 2= x

,g1x 2=-x

+ 4f 1x 2= x

,g1x 2= x

- 2

CHAPTER

5.5 Fitting Quadratic Curves to Data

If the scatter plot of a data set indicates that the data seem to be best modeled by a

quadratic function, then we can use the QuadReg feature on a graphing calculator

to find the quadratic curve

that best fits the data.

y = ax

+ bx + c

SKILLS

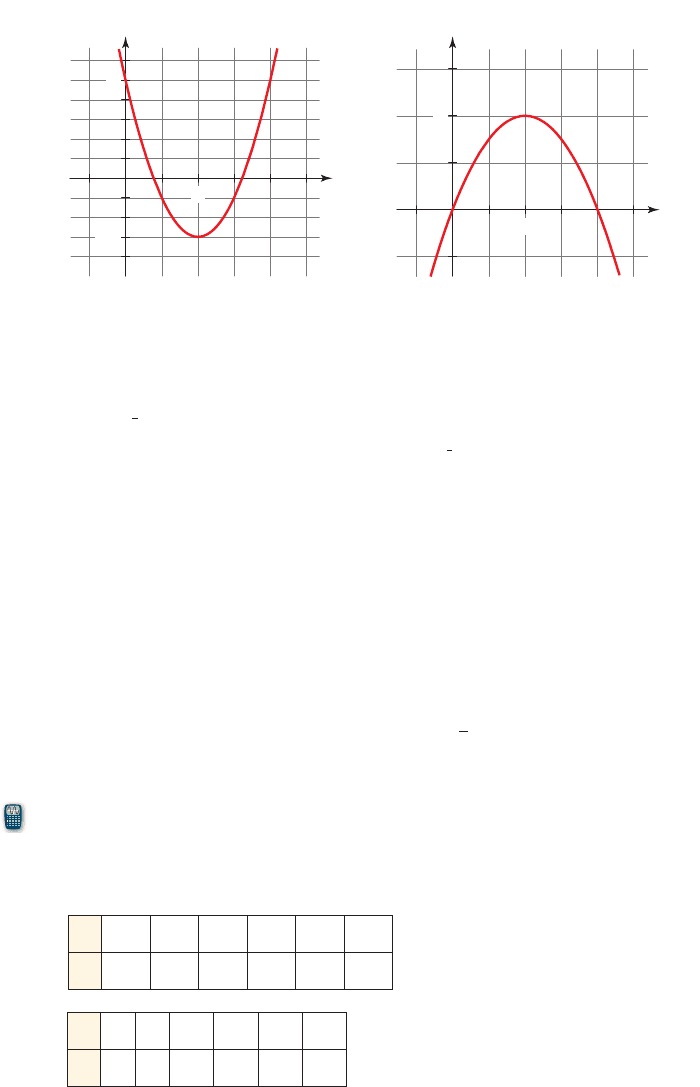
x 0.5 1.0 1.7 2.2 2.5 3.0

y 6.0 3.4 2.0 2.3 3.2 5.6

x 0 2 6 7 11 20

y 5 8 24 23 18 37

CHAPTER 5

■

Review Exercises 469

21–22 ■ Find the quadratic function whose graph is shown.

21. 22.

f 1x 2= ax

+ bx + c

23–28 ■ Find the maximum or minimum value of the function, and find the x-coordinate

of the point at which the maximum or minimum occurs.

23. 24.

25. 26.

27. 28.

29–32

■ Solve the equation by factoring.

29. 30.

31. 32.

33–38 ■ A quadratic equation is given.

(a) Find the discriminant of the equation. How many real solutions does the equation

have?

(b) Solve the equation (if it has real solutions).

33. 34.

35. 36.

37. 38.

39–40

■ A set of data is given.

(a) Use a graphing calculator to find the quadratic model that best fits the data.

(b) Make a scatter plot of the data, and graph the function you found in part (a) on the

scatter plot. Does the model seem to fit the data well?

39.

+ 10 = 10xx

+ 2x + 5 = 0

+ 212x + 2 = 04x

+ 1 = 4x

- 3x - 1 = 0x

+ 3x - 4 = 0

= x + 22x

+ 5x = 3

- 6x + 8 = 0x

+ 7x = 0

f 1x 2=

+ 2x - 3f 1x 2= 15x - 5x

f 1x 2= 2 - 6x + 3x

f 1x 2=-

- x + 1

f 1x 2=-2x

+ 10x + 65f 1x 2= x

+ 4x - 7

40.

470 CHAPTER 5

■

Quadratic Functions and Models

These exercises test your understanding by combining ideas from several sections in a

single problem.

41. The Form of a Quadratic Function In this chapter we have worked with three

different ways of writing the equation for a quadratic function:

■

General form:

■

Standard form:

■

Factored form:

(a) What does the number c represent in the general form?

(b) What do the numbers h and k represent in the standard form?

(d) The graph of a quadratic function has x-intercepts 2 and 5 and y-intercept . On

the basis of the fact that you have been given the x-intercepts, which of the three

forms should you use to find the equation of the function? Use that form to find the

equation.

(e) The graph of a quadratic function has vertex and one x-intercept at 8.

Which of the three forms should you use to find the equation of the function? Use

that form to find the equation.

(f) The graph of the quadratic function f is the same as that of the function

, except that it has been shifted downward so that . Which

of the three forms should you use to find the equation of f ? Use that form to find

the equation.

(g) Find the maximum or minimum value of each of the functions you found in parts

(d), (e), and (f).

42. The Parts of a Parabola In this problem we’ll see how the vertex and the x-intercepts

of a parabola are related to each other.

(a) A parabola has the equation . Find the x-intercepts of the parabola.

(b) Find the vertex of the parabola in part (a). How is the x-coordinate of the vertex

related to the x-intercepts?

of the vertex and the x-intercepts also holds for the parabola .

(d) If a parabola has x-intercepts 1 and 7, what must the x-coordinate of its vertex be?

Find an equation for such a parabola with y-intercept .

(e) Find an equation for the quadratic function whose graph has x-intercepts 3 and 9

and whose maximum value is 27.

43. Height of a Stone Two stones are dropped simultaneously, one from the 24th floor

and the other from the 32nd floor of a high-rise building. After t seconds, the one

dropped from the 24th floor is at a height above the ground, and the

one dropped from the 32nd floor is at a height above the ground.

(The heights are measured in feet.)

(a) Sketch graphs of and on the same coordinate axes.

(b) What transformation would you need to perform on the graph of to get the graph

of ? Express in terms of .

44. Height of a Stone (Refer to Exercise 43.) Suppose that another stone is dropped

from the 24th floor 5 seconds after the first one.

(a) What transformation would you have to perform on the function to obtain a

function

H that models the height of this new stone above the ground t seconds

after the first stone was dropped (where )?

(b) Have the first two stones already hit the ground when the last one is dropped, or is

one (or both) still in the air?

t Ú 5

1t 2= 320 - 16t

1t 2= 240 - 16t

- 3

y = x

+ 4x - 5

y = x

- 6x

f 12 2= 5g1x 2= 3x

+ 6x

14, - 62

- 20

f 1x2= a1x - m 21x - n 2

f 1x2= a1x - h 2

+ k

f 1x2= ax

+ bx + c

CONTEXTS

CONNECTING

THE CONCEPTS

CHAPTER 5

■

Review Exercises 471

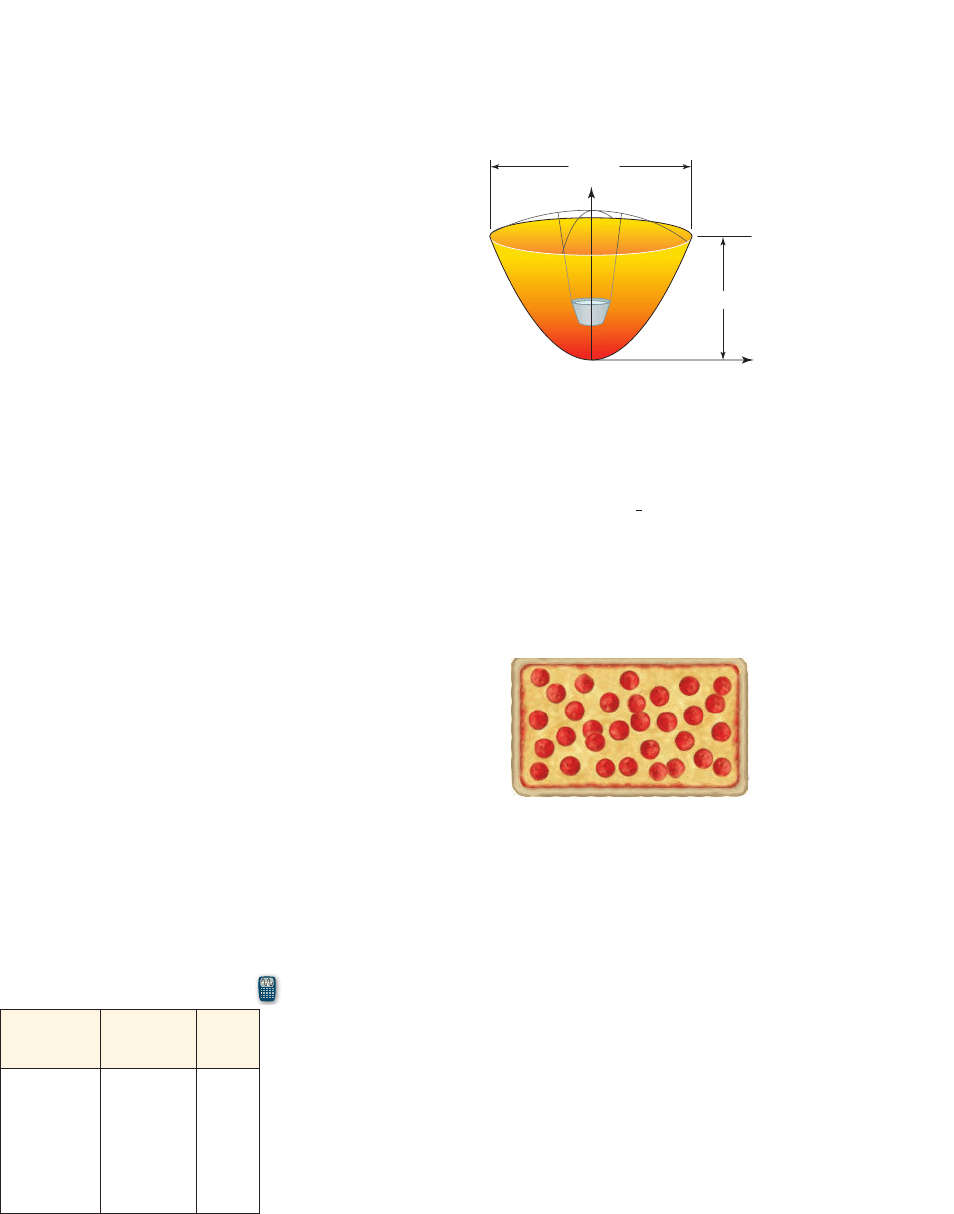
45. Parabolic Cooker Solar cookers are parabolic reflectors that concentrate the light

and heat of sunlight at one spot, where a pot of food can be placed to cook. They are

sometimes sold in camping stores and are also increasingly used in impoverished areas

of the world where cooking fuel is scarce. The figure shows a parabolic bowl-shaped

cooker in cross-section; the width is 32 inches, and the depth is 24 inches. Find a

squaring function that models the shape of the cooker.

24 in.

x+3

Container

Fertilizer

(g)

Yield

(oz)

1 2.0 14.3

2 2.8 18.5

3 3.6 20.8

4 4.4 22.0

5 5.2 21.8

6 6.0 20.1

46. Parabolic Cooker (Refer to Exercise 45.) The width of a solar cooker determines

how much solar energy it gathers. Its depth determines how close the “hot spot” is to the

vertex: The deeper the bowl, the closer to the vertex the cooking pot can be placed. A

new variety of solar cooker has the same width, 32 inches, as the one in Exercise 45, but

its shape is modeled by the function instead. How deep is this new cooker?

47. Dimensions of a Rectangular Pizza Squarehead Pizza Parlor bakes its pizzas in the

shape of rectangles that are all 3 inches longer than they are wide.

(a) Find a function A that models the area of a pizza in terms of its width x.

(b) If a small pizza has an area of 88 square inches, what are its dimensions?

f 1x 2=

48. Maximizing Revenue Miriam sells souvenir caps to tourists in a beach town. She

observes that if she charges x dollars per cap, then she sells about caps per day. (Notice

that the higher her price, the fewer caps she sells.)

(a) Explain why her revenue per day is given by the function .

(b) What price should she charge so that her revenue is as large as possible?

49. Horticulture Experiment A student performs an experiment to determine how much

of a certain fertilizer should be applied to wheat seedlings to produce the maximum

yield. He plants wheat in six identical containers and applies different amounts of

fertilizer to each container. After the wheat reaches maturity, he harvests it and weighs

each “mini-crop.” His results are shown in the table.

(a) Use a graphing calculator to find the quadratic model that best fits the data.

(b) Draw a scatter plot of the data, together with the quadratic function you found in

part (a). Does the model seem to fit the data well?

yield.

R1x 2= x148 - 1.6x 2

472 CHAPTER 5

■

Quadratic Functions and Models

TEST

1. Use the graph of to graph the following functions.

(a)

(b)

(c)

2. Let .

(a) Express f in the standard form of a quadratic function.

(b) What is the vertex of the graph of f ?

(d) Sketch the graph of f.

(e) Does f have a maximum or a minimum value? What is that value?

3. Find a quadratic function f whose graph has vertex and whose y-intercept is 2.

4. For each equation, use the discriminant to determine how many real solutions each

equation has, and then find all real solutions.

(a)

(b)

(c)

5. (a) Use a calculator to find the quadratic function that best models the data in the table.

(b) Make a scatter plot of the data, and graph the function you found in part (a) on the

scatter plot. Does the function seem to fit the data well?

= 3x - 2

- 6x + 7 = 0

+ 5x - 2 = 0

14, - 62

f 1x 2=-x

+ 4x + 12

k1x 2= 31x + 2

h1x 2= 2 - 1x

g1x 2= 1x - 2

f 1x 2= 1x

6. A cannonball that is fired out to sea from a shore battery follows a parabolic trajectory

given by the graph of the equation

where is the height of the cannonball above the water when it has traveled a

horizontal distance of x feet.

(a) What is the maximum height that the cannonball reaches?

(b) How far does the cannonball travel horizontally before splashing into the water?

h1x 2

h1x 2= 10x - 0.01x

CHAPTER

x 0.3 0.5 1.9 2.0 2.4 2.6 2.6 2.9

y 3.2 4.3 5.8 5.7 5.9 5.2 5.4 3.9

h(x)

Transformation Stories

OBJECTIVE To explore the relationship between graphical, algebraic, and verbal

descriptions of transformations of functions in a real-world context.

In Exploration 3 following Chapter 1 we investigated how a graph of a real-world

situation tells a story about that situation. Now that we have studied about transfor-

mations of functions, we can use graphs to tell even more elaborate stories.

In this exploration we investigate traveling salesman Jerome’s original trip and

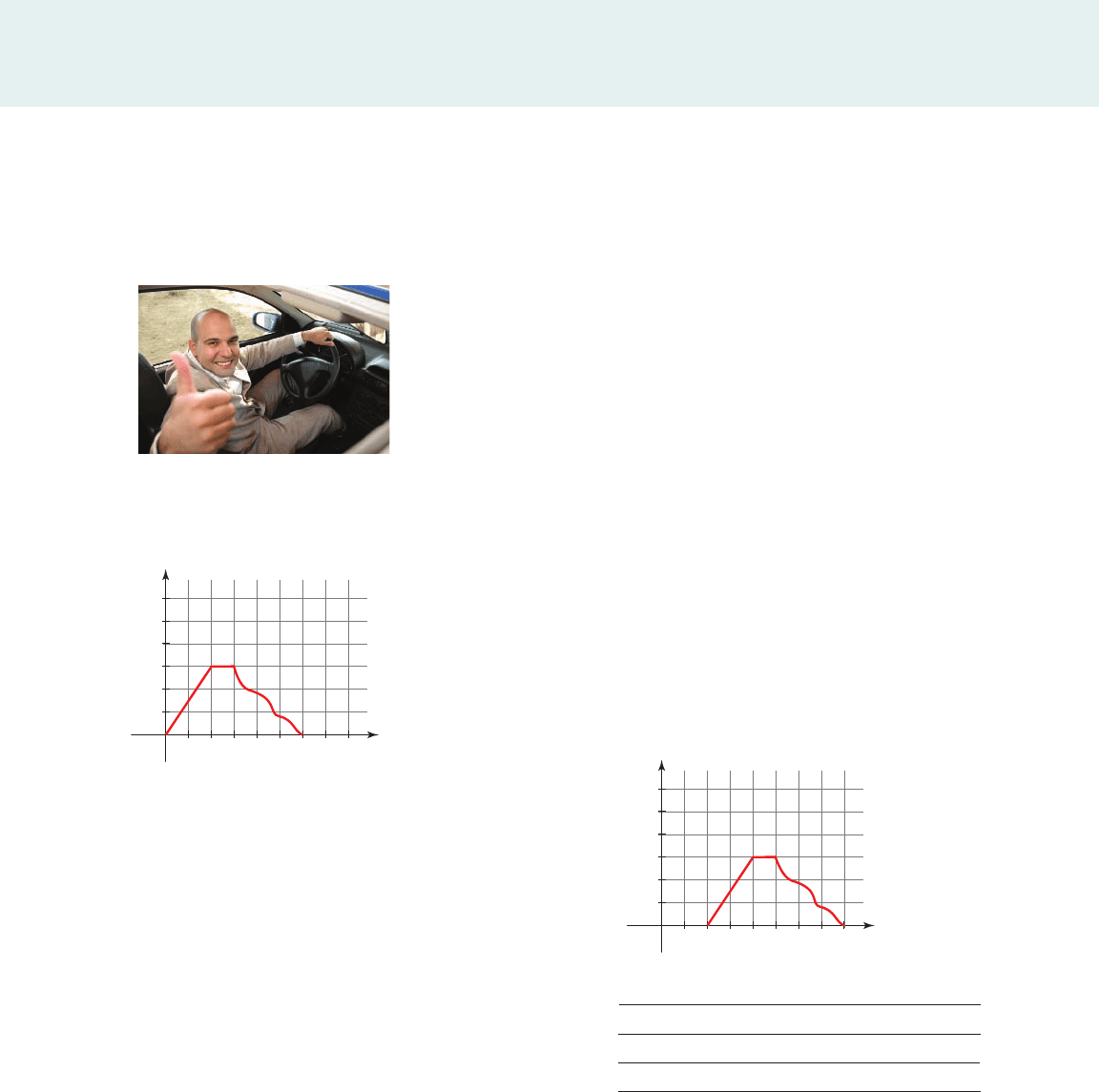
some of its transformations. The graph in the margin shows Jerome’s distance

in miles from his home t hours after 12:00 noon (time 0). We assume that Jerome

travels along a straight road from home to work and back.

Here is the story this graph tells about Jerome’s trip: He starts at noon and travels

at a steady speed of 30 miles per hour until 2:00 P.M. (We know this because the graph

is a straight line with slope 30.) He stops for the next hour (from 2:00 to 3:00 P.M.),

perhaps for a business meeting, at a location 60 miles from his home. He starts driv-

ing back at 3:00 P.M. and arrives home at 6:00 P.M. He travels at various speeds, but his

average speed for the trip back home is 20 miles per hour.

I. Reading a Transformation Story from a Graph

Let’s look at some graphs of transformations of Jerome’s trip. For each graph, state

what the transformation is in words, then in symbols, and then describe the story that

the graph tells about Jerome’s transformed trip.

1. The graph below gives Jerome’s distance from home at time t.A1t2

F1t 2

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

Traveling salesman

d (mi)

t (h)

12345678

100

120

Traveling salesman Jerome’s

original trip

Vladimir Mucibabic/Shutterstock.com

Verbal: Shift to the right 2 units

Symbolic: A(t) (t )

Story: The trip is exactly the same as the original trip,

but he started two hours later (at 2 P.M.).

ⴚ 2ⴝ F

d (mi)

t (h)

12345678

100

120

EXPLORATIONS 473