Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

434 CHAPTER 5

■

Quadratic Functions and Models

! , @

2_1

Vertex

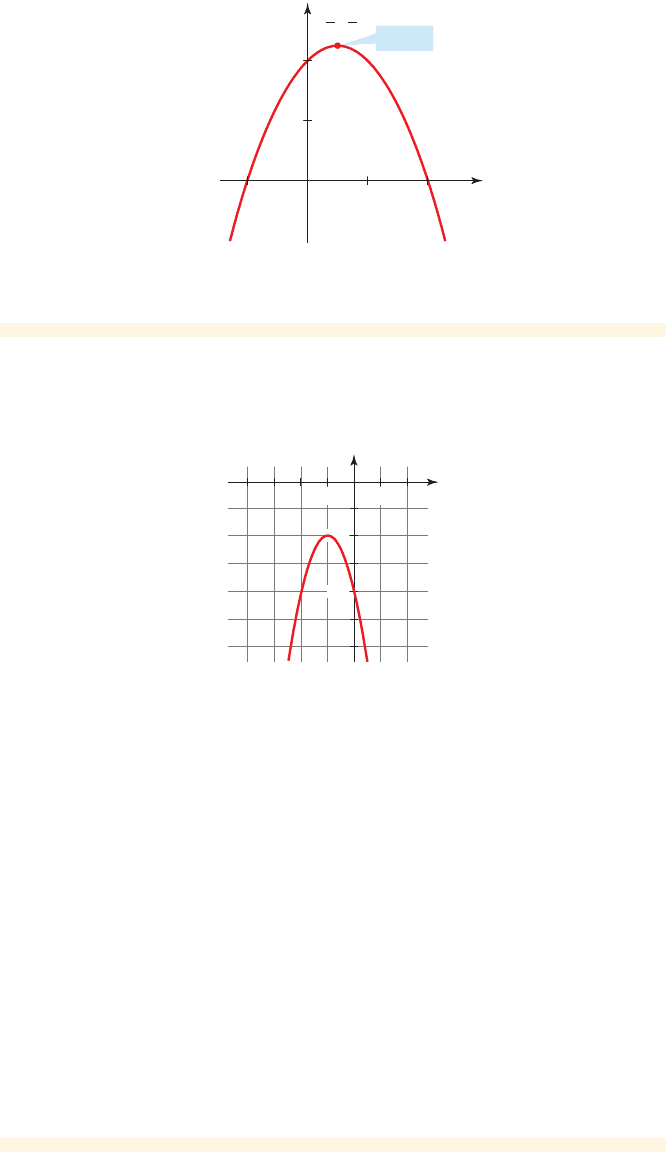
figure 4 Graph of f 1x 2=-x

+ x + 2

The parabola opens downward because the coefficient of the square term

is , which is negative. Since , the y-intercept is 2. The graph is

shown in Figure 4.

f 102= 2- 1

■ NOW TRY EXERCISE 33 ■

example

Finding a Quadratic Function from Its Graph

Find the quadratic function f whose graph is shown in Figure 5.

_1 1

figure 5

Solution

We observe from the graph that the vertex is , so replacing h by and k

by in the standard form of a quadratic function, we have

Standard form

Replace h by , k by

Simplify

We also observe from the graph that the y-intercept is , and hence is . We

can use this to find the value of a:

Replace x by 0

Replace by

Add 2 and switch sides

So the function we seek is .

■ NOW TRY EXERCISE 39 ■

f 1x2=-21x + 1 2

- 2

a =-2

- 4f 10 2 - 4 = a - 2

f 10 2= a10 + 12

- 2

- 4f 10 2- 4

f 1x 2= a1x + 12

- 2

- 2- 1 f 1x2= a1x - 1- 1 22

- 2

f 1x 2= a1x - h2

+ k

- 2

- 11- 1, - 22

SECTION 5.2

■

Quadratic Functions and Their Graphs 435

Check your knowledge of expanding quadratic expressions and completing the

square by doing the following problems. You can review these topics in

Algebra

Toolkits B.1

and

B.2

on pages T25 and T33.

1. Expand each expression.

(a) (b)

2. Determine whether the given expression is a perfect square.

(a) (b) (c) (d)

3. Factor the given perfect square.

(a) (b) (c) (d)

4. Add the appropriate constant to make a perfect square.

(a)

(b)

(c)

(d)

5. Add and subtract the appropriate constants to complete the square.

(a)

(b)

(c)

(d)

- s + 1 = 31s

s + ____2- ____ + 1

+ 8w = 21w

+ 4w + ____2- ____

- y = 1y

- y + ____2- ____

+ 6x = 1x

+ 6x + ____2- ____

4√

- 20√ + ____ = 41√ - ____2

+ 18u + ____ = 31u + ____2

- 20t + ____ = 1t - ____2

+ 10x + ____ = 1x + ____2

+ 5s +

- w +

- 16t + 64x

+ 14x + 49

+ 2w +

- 20t + 100t

- 10t + 100x

+ 6x + 9

16 + 3√216 - 3√213r - 2212r - 32

12t - 521t + 1 21x + 221x - 32

5.2 Exercises

CONCEPTS

Fundamentals

1. To put the quadratic function in standard form, we complete the

_______.

2. The quadratic function is in standard form.

(a) The graph of f is a parabola with vertex (

____, ____).

(b) If , the graph of f opens

_______ (upward/downward).

3. The graph of is a parabola that opens

_______, with its vertex at

(

____, ____).

4. The graph of is a parabola that opens

_______, with its vertex

at (

____, ____).

Think About It

5. Consider the quadratic function .

(a) In general form,

_______.

(b) From the general form we see that the y-intercept is

_______.

y =

y = 1x - 2 21x - 4 2

f 1x 2=-21x + 32

+ 5

f 1x 2= 21x - 32

+ 5

a 6 0

a 7 0

f 1x 2= a1x - h2

+ k

f 1x 2= ax

+ bx + c

436 CHAPTER 5

■

Quadratic Functions and Models

SKILLS

7–8 ■ Determine whether the given function is a quadratic function.

7. (a) (b) (c)

8. (a) (b) (c)

9–16

■ Express the function in the general form of a quadratic function.

9. 10.

11. 12.

13. 14.

15. 16.

17–20

■ A quadratic function f and its graph are given.

(a) Express the function in standard form.

(b) Find the coordinates of the vertex from the standard form.

17. 18. f 1x 2=-

- 2x + 6f 1x 2=-x

+ 6x - 5

f 1x 2=-14x - 12

+ 10f 1x 2= 415x + 32

+ 7

f 1x 2= 1x + 22

- 3f 1x 2= 1x - 12

+ 5

f 1x 2= 13x - 2213x + 22f 1x 2= 12x + 5212x - 52

f 1x 2= 15x - 7213x - 22f 1x 2= 12x + 3214x - 12

f 1x 2= 0.7x

+ 25g1x2= 5x

+ 2x

+ xf 1x 2= 22x

- 3x + 22

f 1x 2= 5

x + 1g1x 2= 3x

+ 2x

+ 1f 1x 2=

+ 2x + 1

6. Consider the quadratic function .

(a) In general form, _______.

(b) From the general form we see that the y-intercept is

_______.

y = 1x - 3 21x - 5 2

y =

y = 1x - m 21x - n 2

19. 20. f 1x 2= 3x

+ 6x - 1f 1x 2= 2x

- 4x - 1

21–24 ■ Express the function in the standard form of a quadratic function.

21. 22.

23. 24. f 1x 2= 3x

- 18x - 5f 1x 2= 2x

+ 20x + 1

f 1x 2= x

- 4x + 2f 1x2= x

+ 2x - 5

SECTION 5.2

■

Quadratic Functions and Their Graphs 437

25–34 ■ A quadratic function is given.

(a) Express the quadratic function in standard form.

(b) Find its vertex.

25. 26.

27. 28.

29. 30.

31. 32.

33. 34.

35–38

■ Find a function f whose graph is a parabola with the given vertex and that passes

through the given point.

35. Vertex ; passes through the point

36. Vertex ; passes through the point

37. Vertex ; passes through the point

38. Vertex ; passes through the point

39–42

■ Find a quadratic function f whose graph is shown.

39. 40.

1- 3, 3021- 5, 62

11, - 8213, 42

14, 16 211, - 22

1- 1, - 821- 2, - 32

f 1x 2= 2x

+ 10x - 1f 1x 2=-x

- 3x + 3

f 1x 2=-x

- 4x + 4f 1x 2=-x

+ 6x + 4

f 1x 2= x

- 2x + 2f 1x2= 2x

+ 4x + 3

f 1x 2= 2x

+ 6xf 1x2=-x

+ 10x

f 1x 2= x

+ 8xf 1x2= x

- 6x

(1, 2)

(_2, _1)

(_2, 5)

(4, 3)

41. 42.

43–44

■ A linear function f and a quadratic function are given.

(a) Complete the table, and find the average rate of change of each function on

intervals of length 1 for x between 0 and 5.

(b) Sketch a graph of each function.

438 CHAPTER 5

■

Quadratic Functions and Models

43. ; g1x 2= 3x

f 1x 2= 3x

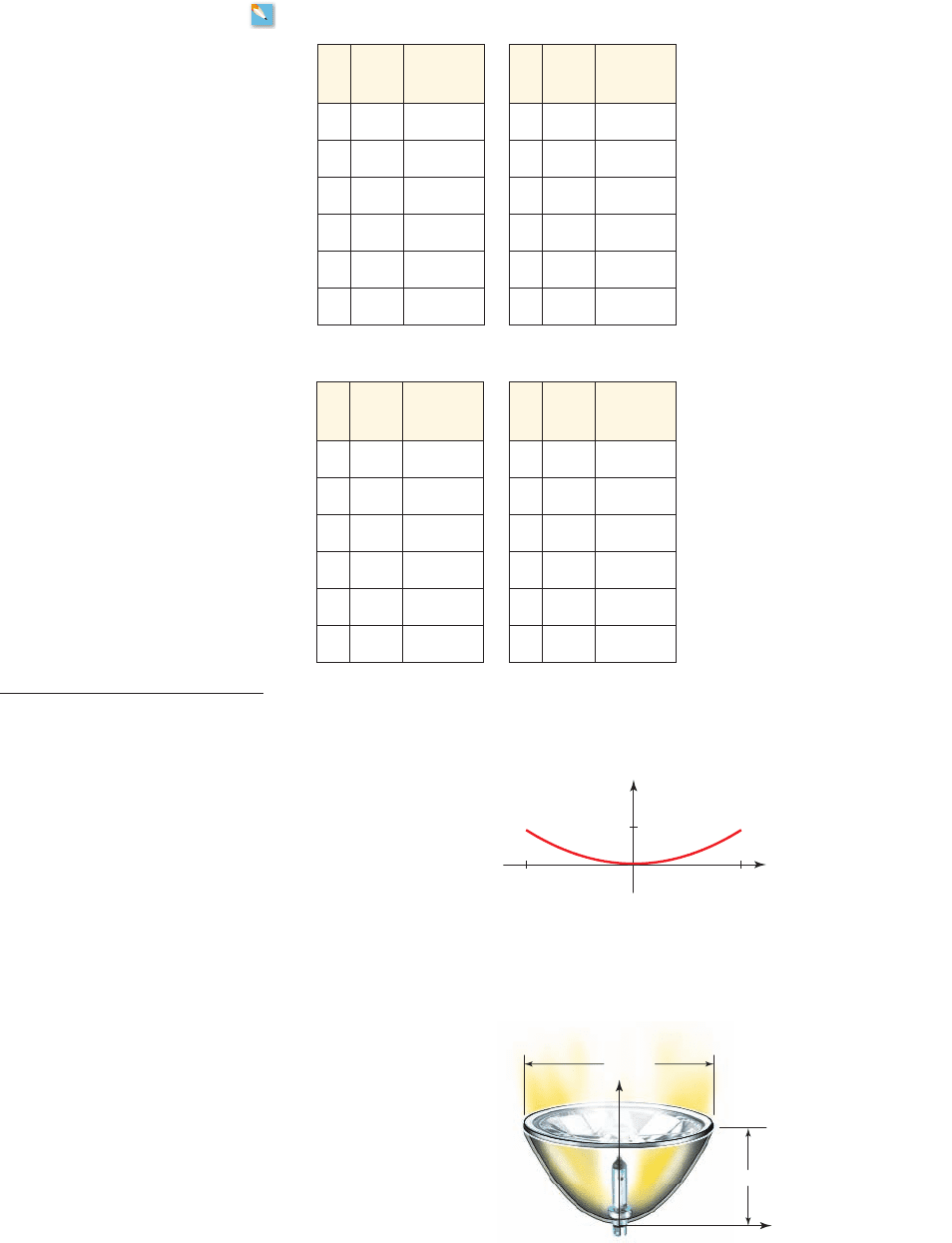
45. Satellite Dish A reflector for a satellite dish is parabolic in cross section. The

reflector is 1 ft deep and 20 ft wide from rim to rim (see the figure). Find a quadratic

function that models the parabolic part of the dish.

46. Parabolic Reflector A headlamp of a car headlight has a reflector that is parabolic in

cross section. The reflector is 8 cm deep and 20 cm wide from rim to rim, as shown in

the figure. Find a quadratic function that models the parabolic part of the reflector,

placing the origin of the coordinate axes at the vertex.

f 1x 2

Rate of

change

0 0 —

1 20

g1x 2

Rate of

change

0 0 —

1 15

CONTEXTS

f 1x 2

Rate of

change

0 0 —

1 3

g1x 2

Rate of

change

0 0 —

1 3

44. ; g1x2= 15x

f 1x 2= 20x

8 cm

20 cm

SECTION 5.3

■

Maxima and Minima: Getting Information from a Model 439

47. Suspension Bridge In a suspension bridge, the shape of the suspension cables is

parabolic. The bridge shown in the figure has towers that are 600 m apart, and the

lowest point of the suspension cables is 150 m below the top of the towers, as shown in

the figure. Find a quadratic function that models the parabolic part of the cables, placing

the origin of the coordinate axes at the vertex.

48. Parabolic Truss Bridge The shape of a suspension bridge can be turned upside down

to create a bridge where each supporting truss is in the shape of a parabola. The truss of

the bridge shown in the figure is 45 feet high at its highest point, and the two points

where it touches the ground are 60 feet apart, as shown in the figure. Find a quadratic

function that models the parabolic truss.

600 m

150 m

x (ft)

45 ft

30 60

y (ft)

5.3 Maxima and Minima: Getting Information from a Model

■

Finding Maximum and Minimum Values

■

Modeling with Quadratic Functions

IN THIS SECTION… we learn how to find the maximum or minimum value of a

quadratic function. We then model real-world situations with quadratic functions and use

the maximum or minimum value to get information about the thing being modeled.

The human race has always been fascinated by projectiles—throwing balls, hurling

spears, or launching rockets. Today, interest in rocketry is very high, as is indicated

by the large number of amateur rocket clubs. One of the main questions in “rocket

science” is: How high will a rocket reach?

In Section 4.2 we observed that gravity pulls down on objects according to a

squaring rule: An object falls feet in t seconds. Now suppose a rocket is

launched at an initial speed of 800 ft/s. If there were no gravity, the rocket would con-

tinue traveling at this same speed indefinitely, so it would reach a height of 800t feet

after t seconds. But because of the pull of gravity, the rocket reaches a height of only

, where h is measured in feet and t in seconds. Now, to find theh = 800t - 16t

16t

Amateur rocket science

istockphoto.com/Robert Launch

440 CHAPTER 5

■

Quadratic Functions and Models

■ Finding Maximum and Minimum Values

The maximum value of a function occurs at the highest point on the graph of the

function, and the minimum value occurs at the lowest point on the graph of the func-

tion. So to find the maximum value (or minimum value) of a quadratic function

, we look at the graph of the function. If , then the graph

of f is a parabola that opens upward, so the function has a minimum value at the

vertex (see Figure 1(a)). On the other hand, if , then the graph of f opens down-

ward, so the function has a maximum value at the vertex (see Figure 1(b)). If f is ex-

pressed in standard form , then the vertex is (h, k), and the

maximum or minimum value of f occurs at . Also,

■

If , then the minimum value of f is .

■

If , then the maximum value of f is .f 1h 2= ka 6 0

f 1h2= ka 7 0

x = h

f 1x2= a1x - h2

+ k

a 6 0

a 7 0f 1x2= ax

+ bx + c

figure

If we are interested only in finding the maximum or minimum value, then a for-

mula is available for doing so. This formula is obtained by completing the square for

the general quadratic function as follows:

Factor a from the x-terms

To complete the square, we add inside the parentheses and subtract out-

side. We get

Complete the square

Factor

= a ax +

+ c -

f 1x 2= a ax

x +

b+ c - a a

a a

= a ax

x b+ c

f 1x 2= ax

+ bx + c

maximum height the rocket reaches, we need to find the maximum value of the quad-

ratic function h.

■

The model gives us the height the rocket reaches at any time.

■

Our goal is to find the maximum height the rocket reaches.

In this section we solve this problem and explore several other real-world problems

that require us to find a maximum (or minimum) value of a quadratic function (see

Example 2). So we begin by developing algebraic formulas for finding these values.

(h, k)

(

)

Minimum

value is k

(

)

(h, k)

Maximum

value is k

SECTION 5.3

■

Maxima and Minima: Getting Information from a Model 441

The x-coordinate of the maximum or minimum value of a quadratic function

occurs at

If , then the minimum value is .

If , then the maximum value is .f a-

ba 6 0

f a-

ba 7 0

x =-

f 1x2= ax

+ bx + c

This equation is in standard form with and .

Since the maximum or minimum value occurs at , we have the following result.

Maximum or Minimum Value of a Quadratic Function

x = h

k = c -

h =-

example

Finding Maximum and Minimum Values of Quadratic Functions

Find the maximum or minimum value of each quadratic function.

(a) (b)

Solution

(a) This is a quadratic function where a is 1 and b is 4. Thus the maximum or

minimum value occurs at

Formula

Replace a by 1 and b by 4

Calculate

Since , the function has the minimum value

(b) This is a quadratic function where a is , b is 4, and c is . Thus the

maximum or minimum value occurs at

Formula

Replace a by and b by 4

Calculate

Since , the function has the maximum value

■ NOW TRY EXERCISES 9 AND 11 ■

f 112=-211 2

+ 411 2- 5 =-3

a 6 0

= 1

- 2 =-

21- 22

x =-

- 5- 2

f 1- 22= 1- 22

+ 41- 22=-4

a 7 0

=-2

x =-

f 1x2=-2x

+ 4x - 5f 1x2= x

+ 4x

The minimum value occurs at

.x =-2

The maximum value occurs at

.x = 1

442 CHAPTER 5

■

Quadratic Functions and Models

■ Modeling with Quadratic Functions

Now we study real-world phenomena that are modeled by quadratic functions.

example

Maximum Height for a Model Rocket

A model rocket is shot straight upward with an initial speed of 800 ft/s, and the

height of the rocket is given by

where h is measured in feet and t in seconds. What is the maximum height of the

rocket, and after how many seconds is this height attained?

Solution

The function h is a quadratic function where a is and b is 800. Thus the maxi-

mum value occurs when

Formula

Replace a by and b by 800

Calculate

The maximum value is . So the rocket reaches a

maximum height of 10,000 feet after 25 seconds.

■ NOW TRY EXERCISE 23 ■

h =-16125 2

+ 800125 2= 10,000

= 25

- 16 =-

800

21-16 2

t =-

- 16

h = 800t - 16t

example

Maximum Gas Mileage for a Car

Most cars get their best gas mileage when traveling at a relatively moderate speed.

The gas mileage M for a certain new car is modeled by the function

where s is the speed in miles per hour and M is measured in miles per gallon. What

is the car’s best mileage, and at what speed is it attained?

Solution

The function M is a quadratic function where a is and b is 3. Thus the maximum

value occurs when

Formula

Replace a by and b by 3

Calculate

The maximum value is . So the car’s best

gas mileage is 32 mi/gal, when it is traveling at 42 mi/h.

■ NOW TRY EXERCISE 25 ■

M142 2=-

142 2

+ 3142 2- 31 = 32

= 42

2A-

s =-

M1s 2=-

+ 3s - 3115 … s … 70

The maximum gas mileage occurs

at 42 mi/h.

SECTION 5.3

■

Maxima and Minima: Getting Information from a Model 443

example

Fencing a Garden

A gardener has 140 feet of fencing to fence in a rectangular vegetable garden.

(a) Find a function that models the area of the garden in terms of the width of the

garden.

(b) Find the largest area she can fence and the dimensions of that area.

Solution

(a) In Example 5 of Section 1.8 (page 94) we found that the function that models

the area she can fence is

where x is the width of the garden in feet, and is the length in feet.

(See Figure 2.)

(b) In Section 1.8 we found the maximum value of the function A graphically.

Here we find the maximum area algebraically.

The function A is a quadratic function where a is and b is 70. Thus the

maximum value occurs when

Formula

Replace a by and b by 70

Calculate

When the width is 35, the length is , and the maximum area

is . So the largest area she can fence is

1225 square feet, and the dimensions are 35 by 35 feet.

■ NOW TRY EXERCISE 27 ■

A135 2= 701352- 1352

= 1225

70 - 35 = 35

= 35

- 1 =-

21- 12

x =-

- 1

70 - x

A1x 2= 70x - x

70-x

figure 2 Area is

A1x 2= x170 - x 2= 70x - x

Compare with graphical solution in

Example 5 of Section 1.8

(page 94).

example

Maximum Revenue from Ticket Sales

A hockey team plays in an arena that has a seating capacity of 15,000 spectators.

With the ticket price set at $14, average attendance at recent games has been 9500.

A market survey indicates that for each dollar the ticket price is lowered, the aver-

age attendance increases by 1000.

(a) Find a function that models the revenue in terms of ticket price.

(b) Find the price that maximizes revenue from ticket sales.

Solution

(a) The model that we want is a function that gives the revenue for any ticket

price.

There are two varying quantities: ticket price and attendance. Since the

function we want depends on price, we let

Next, we express attendance in terms of x.

x = ticket price

revenue = ticket price * attendance