Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

444 CHAPTER 5

■

Quadratic Functions and Models

150,000

Maximum revenue occurs when the

ticket price is $11.75.

In Words In Algebra

Ticket price x

Amount ticket price is lowered

Increase in attendance

Attendance

The model that we want is the function R that gives the revenue for a given

ticket price x.

(b) Since R is a quadratic function where a is and b is 23,500, the

maximum occurs at

So a ticket price of $11.75 gives the maximum revenue.

■ NOW TRY EXERCISE 33 ■

x =-

23,500

21- 10002

= 11.75

- 1000

R1x 2= 23,500x - 1000x

R1x 2= x123,500 - 1000x 2

R1x 2= x * 39500 + 1000114 - x24

revenue = ticket price * attendance

9500 + 1000114 - x2

1000114 - x2

14 - x

5.3 Exercises

CONCEPTS

Fundamentals

1. The quadratic function is in general form.

(a) The maximum or minimum value of f occurs at

(b) If , then f has a

_______ (maximum/minimum) value.

2. (a) The quadratic function has a

_______

(maximum/minimum) value of  ______.

(b) The quadratic function has a

_______

(maximum/minimum) value of  ______.

Think About It

3. Consider the quadratic function .

(a) In general form,

______________.

(b) The graph is a parabola that opens

_______ (up/down).

_______.

x =

y =

y = 1x - 2 21x - 4 2

f a

ⵧ

f 1x 2=-2x

- 12x + 5

f a

ⵧ

f 1x 2= 2x

- 12x + 5

a 6 0

a 7 0

x =

f 1x 2= ax

+ bx + c

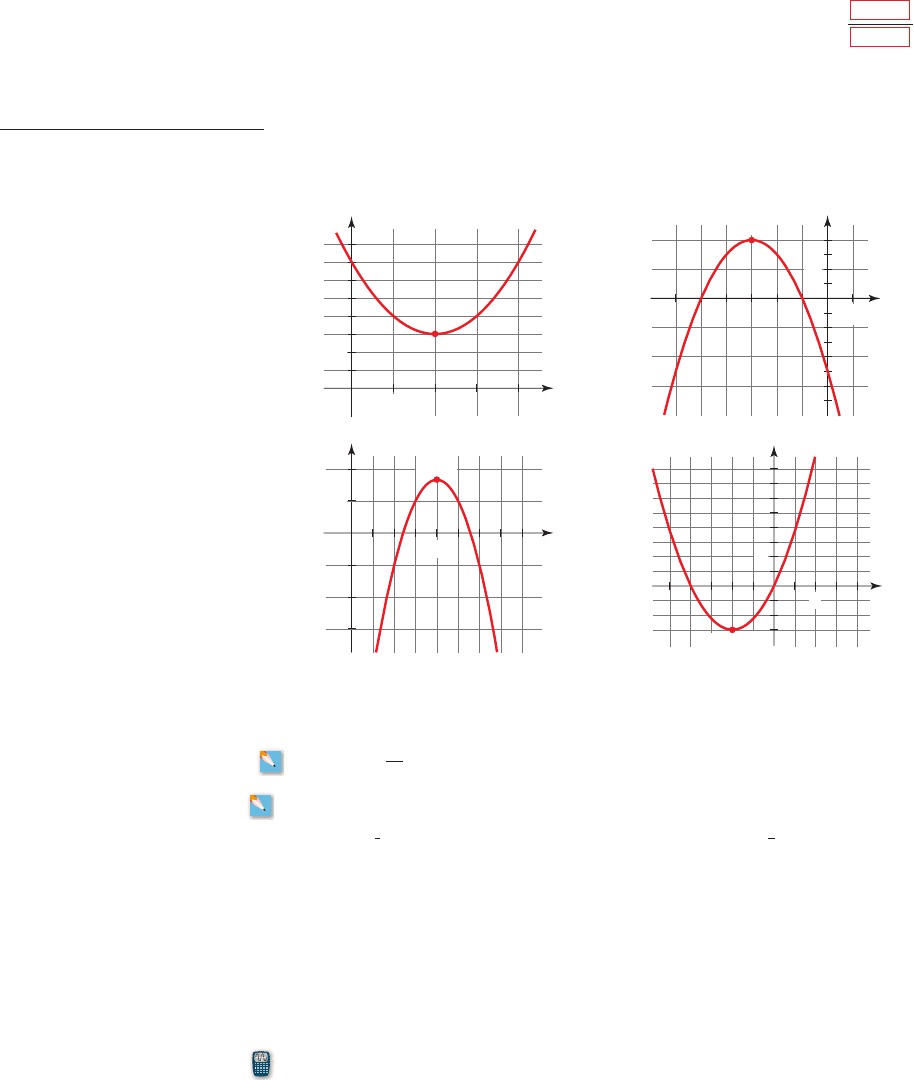
SECTION 5.3

■

Maxima and Minima: Getting Information from a Model 445

SKILLS

4. Consider the quadratic function .

(a) In general form,

______________.

(b) The graph is a parabola that opens

_______ (up/down).

(d) Using the formula in part (c), the minimum value of occurs

when

_______.

5–8

■ A graph of a quadratic function is shown.

(a) Does the function have a minimum or a maximum value? What is that value?

(b) Find the x-value at which the minimum or maximum value occurs.

5. 6.

x =

y = 1x + 3 21x - 5 2

x =

y =

y = 1x - m 21x - n 2

(2, 3)

(_3, 4)

7. 8.

(4, 5)

(_1, _3)

9–14 ■ Find the minimum or maximum value of the quadratic function, and find the

x-value at which the minimum or maximum value occurs.

9. 10.

11. 12.

13. 14.

15–18

■ A quadratic function is given.

(a) Sketch its graph.

(b) Find the minimum or maximum value of f, and find the x-value at which the

minimum or maximum value occurs.

15. 16.

17. 18.

19–22

■ A quadratic function is given.

(a) Use a graphing device to find the maximum or minimum value of the quadratic

function f, correct to two decimal places.

(b) Find the maximum or minimum value of f, and compare it with your answer to part (a).

f 1x 2= 1 - 6x - x

f 1x 2=-x

- 3x + 3

f 1x 2= x

- 8x + 8f 1x2= x

+ 2x - 1

f 1x 2= 3 - x -

h1x 2=

+ 2x - 6

f 1x 2= 1 + 3x - x

f 1x 2= x

+ x + 1

g1x 2= 2x1x - 4 2+ 7f 1x 2=-

+ 2x + 7

446 CHAPTER 5

■

Quadratic Functions and Models

CONTEXTS

19. 20.

21. 22.

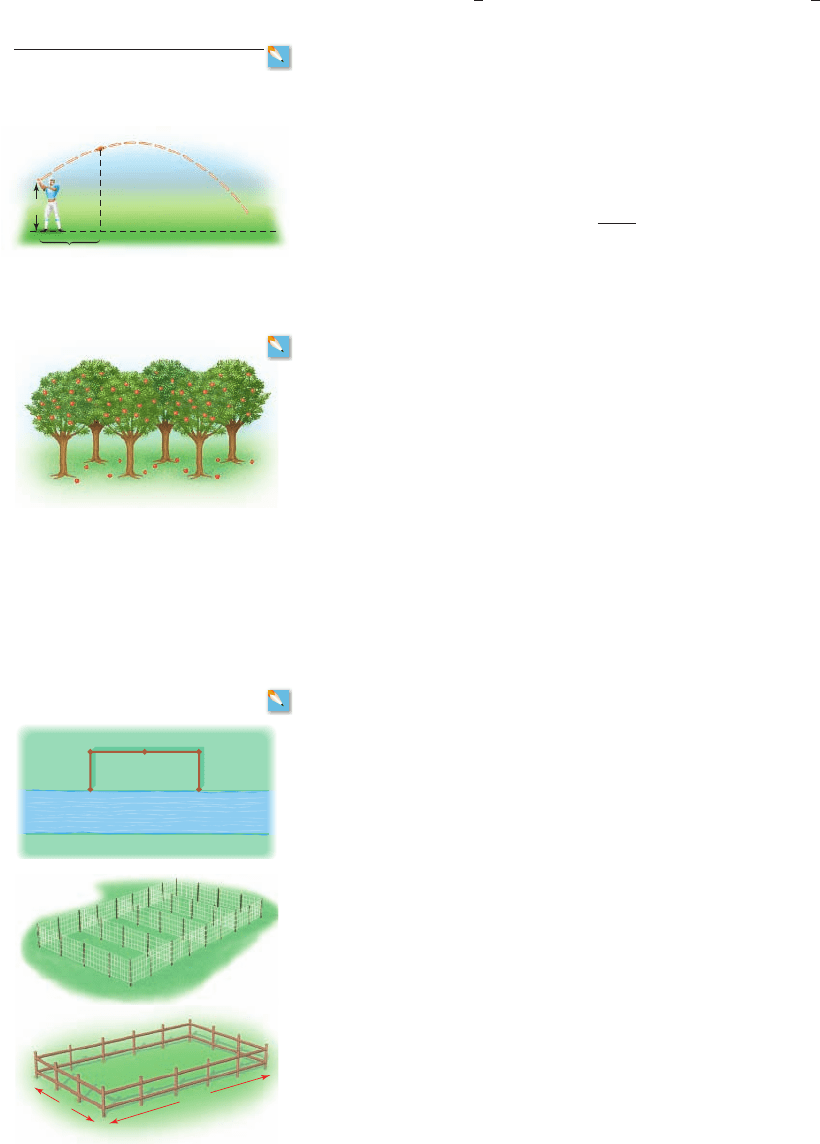
23. Height of a Ball If a ball is thrown directly upward with a velocity of 12 m/s, its

height (in meters) after t seconds is given by . What is the maximum

height attained by the ball, and after how many seconds is that height attained?

24. Path of a Ball A ball is thrown across a playing field from a height of 5 ft above the

ground at an angle of to the horizontal and at a speed of 20 ft/s. It can be deduced

from physical principles that the path of the ball is modeled by the function

where x is the distance in feet that the ball has traveled horizontally and y is the height

in feet. What is the maximum height attained by the ball, and at what horizontal

distance does this occur?

25. Agriculture The number of apples produced by each tree in an apple orchard depends

on how densely the trees are planted. If n trees are planted on an acre of land, then each

tree produces apples. So the number of apples produced per acre is

What is the maximum yield of the trees, and how many trees should be planted per acre

to obtain the maximum yield of apples?

26. Agriculture At a certain vineyard it is found that each grape vine produces about 10

pounds of grapes in a season when about 700 vines are planted per acre. For each

additional vine that is planted, the production of each vine decreases by about 1%. So

the number of pounds of grapes produced per acre is modeled by

where n is the number of additional vines planted. What is the maximum yield of the

grape vines, and how many vines should be planted to maximize grape production?

27. Fencing a Field A farmer has 2400 feet of fencing with which he wants to fence off a

rectangular field that borders a straight river. He does not need a fence along the river

(see the figure).

(a) Find a function A that models the area of the field in terms of one of its sides x.

(b) What is the largest area that he can fence, and what are the dimensions of that area?

[Compare to your graphical solution in Exercise 29, Section 1.8.]

28. Dividing a Pen A rancher with 750 feet of fencing wants to enclose a rectangular

area and then divide it into four pens with fencing parallel to one side of the rectangle

(see the figure).

(a) Find a function A that models the total area of the four pens.

(b) Find the largest possible total area of the four pens and the dimensions of that area.

[Compare to your graphical solution in Exercise 30, Section 1.8.]

29. Fencing a Horse Corral Carol has 1200 feet of fencing to fence in a rectangular

horse corral.

(a) Find a function A that models the area of the corral in terms of the width of the

corral.

A1n 2= 1700 + n2110 - 0.01n2

A1n 2= n1900 - 9n 2

900 - 9n

120 2

+ x + 5

45°

y = 12t - 4.9t

f 1x 2= 3 - 2x - 23x

f 1x 2= 1 + x - 22x

f 1x 2= x

- 3.2x + 4.1f 1x 2= x

+ 1.79x - 3.21

5 ft

600 – x

SECTION 5.3

■

Maxima and Minima: Getting Information from a Model 447

(b) Find the dimensions of the rectangle that maximize the area of the corral.

30. Making a Rain Gutter A rain gutter is formed by bending up the sides of a 30-inch-

wide rectangular metal sheet as shown in the figure.

(a) Find a function A that models the cross-sectional area of the gutter in terms of x.

(b) Find the value of x that maximizes the cross-sectional area of the gutter.

31. Minimizing Area A wire 10 cm long is cut into two pieces, one of length x and the

other of length , as shown in the figure. Each piece is bent into the shape of a

square.

(a) Find a function A that models the total area enclosed by the two squares.

(b) Find the value of x that minimizes the total area of the two squares.

10 - x

30 in.

10 cm

x 10-x

32. Light from a Window A Norman window has the shape of a rectangle surmounted

by a semicircle, as shown in the figure. A Norman window with perimeter 30 feet is to

be constructed.

(a) Find a function that models the area of the window.

(b) Find the dimensions of the window that admits the greatest amount of light.

33. Stadium Revenue A baseball team plays in a stadium that holds 55,000 spectators.

With the ticket price at $10, the average attendance at recent games has been 27,000. A

market survey indicates that for every dollar the ticket price is lowered, the attendance

increases by 3000.

(a) Find a function R that models the revenue in terms of ticket price.

(b) Find the price that maximizes revenue from ticket sales.

34. Maximizing Profit A community bird-watching society makes and sells simple bird

feeders to raise money for its conservation activities. The materials for each feeder cost

$6, and the society sells an average of 20 feeders per week at a price of $10 each. The

society has been considering raising the price, so it conducts a survey and finds that for

every dollar increase, it loses 2 sales per week.

(a) Find a function P that models weekly profit in terms of price per feeder.

(b) What price should the society charge for each feeder to maximize profits? What is

the maximum weekly profit?

448 CHAPTER 5

■

Quadratic Functions and Models

5.4 Quadratic Equations: Getting Information from a Model

■

Solving Quadratic Equations: Factoring

■

Solving Quadratic Equations: The Quadratic Formula

■

The Discriminant

■

Modeling with Quadratic Functions

IN THIS SECTION… we study how to solve quadratic equations. Solving quadratic

equations helps us get information from quadratic models.

GET READY… by reviewing how to factor expressions in Algebra Toolkit B.2. Test

your understanding by doing the Algebra Checkpoint at the end of this section.

In Section 4.3 we found that the height a rocket reaches is modeled by a quadratic

function. In this section we use the model to answer the question “When does the

rocket reach a given height?” (see Example 8).

■

The model gives us the height the rocket reaches at any time.

■

Our goal is to find the time at which the rocket reaches a given height.

We can get the information we want from the model; to do so, we need to solve

a quadratic equation. So we start this section by learning how to solve such

equations.

■ Solving Quadratic Equations: Factoring

A quadratic equation is an equation of the form

where a, b, and c are real numbers with . Some quadratic equations can be

solved by factoring and using the following basic property of real numbers.

Zero-Product Property

a  0

+ bx + c = 0

AB = 0if and only ifA = 0orB = 0

This means that if we can factor the left-hand side of a quadratic (or other) equation,

then we can solve it by setting each factor equal to 0 in turn. This method works only

when the right-hand side of the equation is 0.

example

Solving a Quadratic Equation by Factoring

Solve the equation .

Solution

We must first rewrite the equation so that the right-hand side is 0.

+ 5x = 24

SECTION 5.4

■

Quadratic Equations: Getting Information from a Model 449

Given equation

Subtract 24

Factor

Zero-Product Property

Solve

The solutions are and .

We substitute into the original equation:

✓

We substitute into the original equation:

✓

■ NOW TRY EXERCISE 7 ■

Do you see why one side of the equation must be 0 in Example 1? Factoring the

equation as does not help us find the solutions, since 24 can be

factored in infinitely many ways, such as , and so on.6

48, A-

1- 602

x1x + 5 2= 24

1- 82

+ 51- 82= 64 - 40 = 24

x =-8

132

+ 5132= 9 + 15 = 24

x = 3

✓ CHECK

x =-8x = 3

x =-8 x = 3

x - 3 = 0orx + 8 = 0

1x - 321x + 82= 0

+ 5x - 24 = 0

+ 5x = 24

x- and y-intercepts are reviewed

in Algebra Toolkit D.2, page T71.

example

Graphing a Quadratic Function

Let .

(a) Find the x-intercepts of the graph of f.

(b) Sketch the graph of f, and label the x- and y-intercepts and the vertex.

Solution

(a) To find the x-intercepts, we solve the equation

The equation was solved in Example 1. The x-intercepts are 3 and .

(b) To find the y-intercept, we set x equal to 0:

So the y-intercept is .

The function f is a quadratic function where a is 1 and b is 5. So the

x-coordinate of the vertex occurs at

Formula

Replace a by 1 and b by 5

Calculate

x =-

- 24

f 102= 0 + 5

0 - 24 =-24

- 8

+ 5x - 24 = 0

f 1x2= x

+ 5x - 24

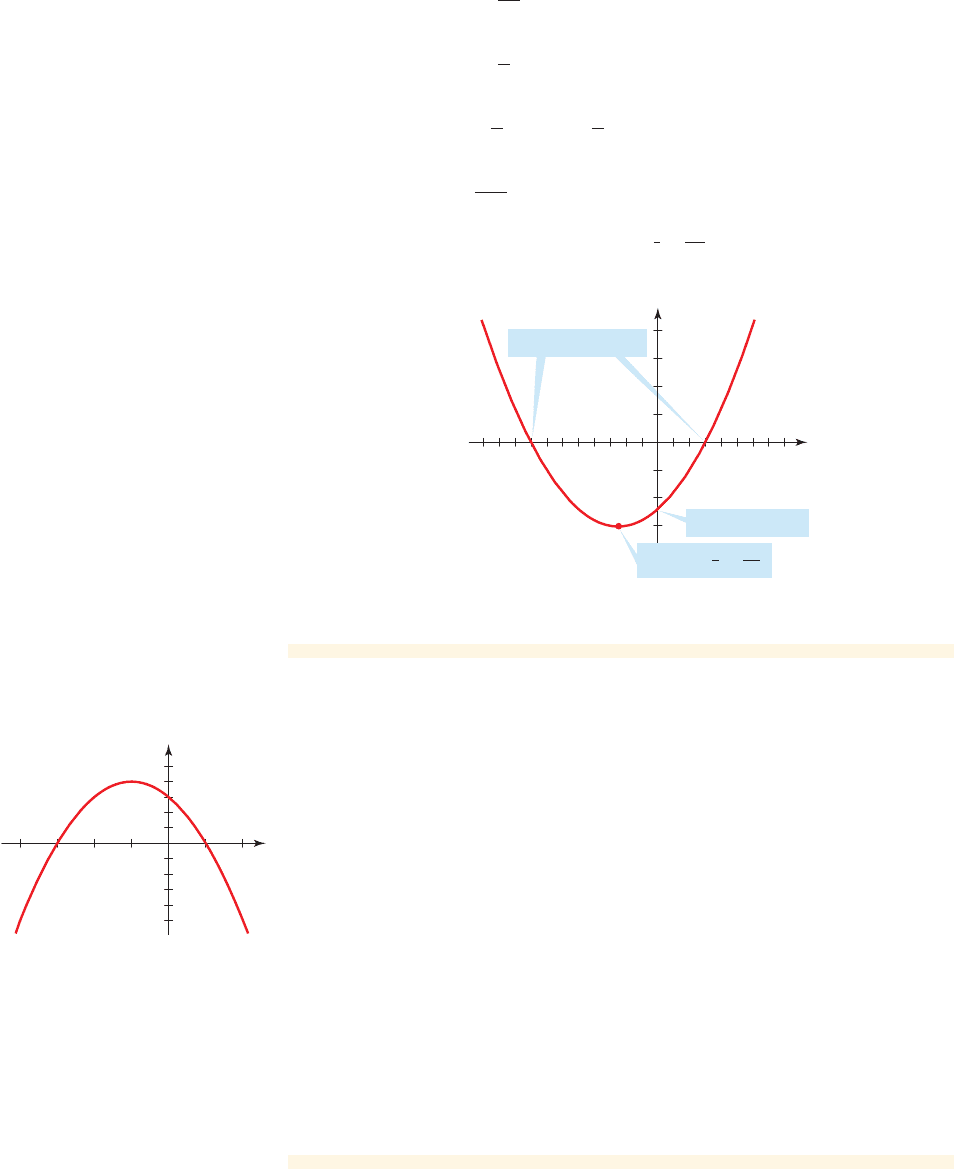
450 CHAPTER 5

■

Quadratic Functions and Models

x-intercepts _8, 3

y-intercept _24

Vertex

()

121

figure 1 Graph of f 1x 2= x

+ 5x - 24

The y-coordinate of the vertex is

Formula

a is 1 and b is 5

Definition of f

Calculate

The graph is a parabola with vertex at . The parabola opens upward

because . The graph is shown in Figure 1.a 7 0

A-

, -

121

= a-

+ 5 a-

b- 24

= f a-

y = f a-

■ NOW TRY EXERCISE 53 ■

example

Finding a Quadratic Function from a Graph

The graph of a quadratic function f is shown in Figure 2. Find an equation that rep-

resents the function f.

Solution

We observe from the graph that the x-intercepts are and 1. So we can express the

function f in factored form:

We need to find a. From the graph we see that the y-intercept is 6, so . We have

Replace x by 0

y-intercept is 6

Simplify

Divide by and switch sides

It follows that .

■ NOW TRY EXERCISE 17 ■

f 1x2=-21x - 1 21x + 32

- 3 a =-2

6 =-3a

6 = a10 - 1 210 + 32

f 10 2= a10 - 1210 + 3 2

f 102= 6

f 1x2= a1x - 1 21x + 3 2

- 3

figure 2

SECTION 5.4

■

Quadratic Equations: Getting Information from a Model 451

■ Solving Quadratic Equations: The Quadratic Formula

If a quadratic equation does not factor readily, we can solve it by using the quad-

ratic formula. This formula gives the solutions of the general quadratic equation

and is derived by using the technique of completing the square

(see

Algebra Toolkit C.3

, page T62).

The Quadratic Formula

+ bx + c = 0

example

Using the Quadratic Formula

Find all solutions of each equation.

(a) (b) (c)

Solution

(a) In this quadratic equation , , and .

By the Quadratic Formula,

If approximations are desired, we can use a calculator to obtain

(b) Using the Quadratic Formula where a is 4, b is 12, and c is 9 gives

This equation has only one solution, .

Since the square of any real number is nonnegative, is undefined in the

real number system. The equation has no real solution.

■ NOW TRY EXERCISES 27, 31, AND 33 ■

1- 1

x =

- 2 ; 22

- 4

- 2 ; 2- 4

- 2 ; 22- 1

=-1 ; 2- 1

x =-

x =

- 12 ; 21122

- 4

- 12 ; 0

x =

5 + 237

L 1.8471andx =

5 - 237

-L-0.1805

x =

- 1- 52; 21- 52

- 413 21- 12

213 2

5 ; 237

c =-1a = 3

- 5x - 1 = 0

b =-5

c is - 1b is - 5a is 3

+ 2x + 2 = 04x

+ 12x + 9 = 03x

- 5x - 1 = 0

The solutions of the quadratic equation , where , are

x =

- b ; 2b

- 4ac

a  0ax

+ bx + c = 0

452 CHAPTER 5

■

Quadratic Functions and Models

■ The Discriminant

The quantity that appears under the square root sign in the Quadratic

Formula is called the discriminant of the equation and is given

the symbol D. If D is negative, then is undefined, so the quadratic equa-

tion has no real solution. If D is zero, then the equation has exactly one real solution.

If D is positive, then the equation has two distinct real solutions. The following box

summarizes these observations.

The Discriminant

- 4ac

+ bx + c = 0

- 4ac

The discriminant of the quadratic equation , where ,

is .

1. If , then the equation has no real solutions.

2. If , then the equation has exactly one real solution.

3. If , then the equation has two distinct real solutions.D 7 0

D = 0

D 6 0

D = b

- 4ac

a  0ax

+ bx + c = 0

We will see in the next example that we can use the discriminant to determine

whether the graph of a quadratic function has two x-intercepts, one x-intercept, or no

x-intercepts.

example

Using the Discriminant to Find the Number of x-Intercepts

A quadratic function is given. Find the discriminant of the

equation , and use it to determine the number of x-intercepts of the

graph of f. Sketch a graph of f to confirm your answer.

(a)

(b)

(c)

Solution

(a) The equation is , so a is 1, b is , and c is 8. The discrimi-

nant is

Since the discriminant is positive, there are two distinct solutions, and hence

there are two x-intercepts for the graph of f. The graph of f in Figure 3(a)

confirms this.

(b) The equation is , so a is 1, b is , and c is 9. The discrimi-

nant is

Since the discriminant is zero, there is exactly one solution and hence one

x-intercept for the graph of f. The graph in Figure 3(b) confirms this.

D = b

- 4ac = 1- 62

- 4

9 = 0

- 6x

- 6x + 9 = 0

D = b

- 4ac = 1- 62

- 4

8 = 32 7 0

- 6x

- 6x + 8 = 0

f 1x2= x

- 6x + 10

f 1x2= x

- 6x + 9

f 1x2= x

- 6x + 8

+ bx + c = 0

f 1x2= ax

+ bx + c

SECTION 5.4

■

Quadratic Equations: Getting Information from a Model 453

_1.5

(a) f(x)=x™-6x+8

_1.5

(b) f(x)=x™-6x+9

_1.5

figure 3

discriminant is

Since the discriminant is negative, there are no solutions, and hence there are

no x-intercepts for the graph of f. The graph in Figure 3(c) confirms this.

D = b

- 4ac = 1- 62

- 4

10 = 36 - 40 =-4 6 0

- 6x

- 6x + 10 = 0

■ NOW TRY EXERCISES 43, 45, AND 47 ■

■ Modeling with Quadratic Functions

We now study real-world phenomena that are modeled by quadratic functions, and

we solve quadratic equations to get information from the model.

example

Dimensions of a Lot

A rectangular building lot is 8 feet longer than it is wide.

(a) Find a function that models the area of the lot for any width.

(b) If the lot has area of 2900 square feet, find the dimensions of the lot.

Solution

(a) We want a function A that models the area of the lot in terms of the width. Let

We translate the information given in the problem into the language of algebra

(see Figure 4).

In Words In Algebra

Width of lot w

Length of lot

Now we set up the model:

A1w 2= w1w + 82

area of lot = width of lot * length of lot

w + 8

w = width of lot

figure 4