Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

(a) Where is the one thousand dollar mark on the logarithm ruler? Where is

the ten thousand dollar mark?

(b) Where are the one million and one billion dollar marks on the ruler?

(d) Is the logarithm ruler too long to handle easily? Can the ruler be easily

used to measure small numbers of dollars?

4. In Questions 1–3 we used graphical methods to help us understand the differ-

ence in size between a million dollars and a billion dollars. Now let’s use

another method.

(a) Suppose you have one million dollars under your mattress (you don’t trust

banks). Each day you take out one thousand dollars and spend it. For how

many years would you be able to maintain this lifestyle before you

become totally broke?

(b) If you have a billion dollars (instead of a million) in part (a), how many

years would pass by before you would be broke?

II. How Small Is a Bacterium?

We’ve talked a lot about bacteria in this book. Let’s compare the size of a bacterium

with other, more familiar things. Recall that a centimeter (cm) is one hundredth of a

meter (m), a millimeter (mm) is a thousandth of a meter, and a micrometer (mm) is

a millionth of a meter.

Small child 1 m

Housefly 1 cm

Mite 1 mm

Bacterium 1 mm

1. To visually compare the size of the living things in the above list, let’s use a

meter stick. Mark the size of each one on the meter stick below.

Money under the mattress

Meter stick

1 m

_7 _6 _5 _4 _3 _2 _1 0 1 2

10–¡ 10º 10¡

arithmic meter stick

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

404 CHAPTER 4

0123456789

10¡

10™

The lo

arithm ruler

cbarnesphotography/Shutterstock.com 2009

2. Some of the marks you put on the meter stick in Question 1 are not easily

distinguishable. Let’s use the logarithmic meter stick shown below.

(a) Express the size (in meters) of each of the living things on the list on the

preceding page in exponential notation.

(b) Label the size of each object on the logarithm meter stick.

rithmic meter stick?

III. Orders of Magnitude

Sometimes we want to make rough size comparisons. To do this, we round off num-

bers to the nearest power of 10. For example, for a man who is 6 feet tall, we round

his height to 10 feet. In other words, the height of the man is closer to feet than

to feet (or 1 foot). For a ladybug that is feet long, we round its length

to feet. A number rounded to the nearest power of 10 is called an order of mag-

nitude. The idea is that an object that is 10 times or so larger than another object is

in a different category or “order of magnitude.”

To compare the height of a human being ( feet) to the height of a ladybug

( feet), we find the ratio:

So a human being is roughly or 1000 times larger than a ladybug. We say that a

human being is 3 orders of magnitude (three powers of 10) greater than a ladybug.

1. Express the following in terms of order of magnitude.

Object Size (m) Order of magnitude

Gold atom ________

Bacterium ________

Mite ________

Ladybug ________

Human ________

Earth ________

Sun ________

Betelgeuse ________

2. Perform the following order of magnitude comparisons using the results of

Question 1.

(a) The sun is _______ orders of magnitude larger than the earth.

(b) A bacterium is _______ orders of magnitude larger than a gold atom.

(d) Betelgeuse is _______ orders of magnitude larger than a bacterium.

8.3 * 10

1.4 * 10

1.3 * 10

1.8 * 10

7.0 * 10

-3

2.0 * 10

-3

3.5 * 10

-6

2.8 * 10

-10

human height

ladybug length

-2

= 10

1 -1-22

= 10

-2

9.0 * 10

-3

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 405

A tree is one order of magnitude

taller than a human.

⫺3

⫺2

Cate Frost/Shutterstock.com

Semi-Log Graphs

OBJECTIVE To make semi-log graphs and use them to find models of exponential

data.

In Chapter 3 we sketched graphs of exponential functions. But in each case we

sketched only a small portion of the graph. This is because exponential functions

grow so rapidly that we would need a sheet of paper larger than the pages of this book

to sketch them, even for relatively small input values. In this exploration we see how

logarithms can be used to help us manage the size of such large graphs. In the process

we’ll discover how logarithms allow us to “straighten” exponential graphs, helping

us to analyze their properties as easily as we analyze lines.

I. How Big Is the Graph?

Let’s see what size sheet of paper we need to sketch a graph of

for x between 0 and 8.

1. For the function f, the input values of 0 and 8 correspond to what output values?

Input value Output value

0 _______

8 _______

2. Let’s make each unit on our graph to be 1 inch. So we need just 8 inches for

the x-axis, which is the width of the pages of this book.

(a) How many inches would we need for the y-axis?

(b) To get a better idea of how long the y-axis needs to be, convert your

answer to part (b) into miles.

3. What if we decide to let each inch on the y-axis represent 1000 (or ) units?

(a) How many inches would we need for the y-axis?

(b) Convert your answer to part (b) into miles.

4. Two graphs of f are shown below. Which graph can be used to estimate the

values of ? ? ? ?f 1- 0.92f 13.12f 12.3 2f 10.52

f 1x2= 10

0.5 1.0_0.5_1.0

3241_1

2000

4000

6000

8000

10,000

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

406 CHAPTER 4

II. Semi-Log Graphs

None of the graphs we considered in Part I give a satisfactory representation of an

exponential function. One way around this dilemma is to use a “logarithmic ruler”

or logarithmic scale on the y-axis. (See the figure in the margin.)

When we graph a function and use a logarithmic scale on one of the axes, the

resulting graph is called a semi-log graph or semi-log plot. This is equivalent to

graphing the points (x, log y).

■

To draw a graph of f, we plot the points (x, y).

■

To draw a semi-log graph of f, we plot the points (x, log y).

Let’s sketch a semi-log graph of the exponential function

for x between 0 and 10.

1. Complete the table for the values of y and log y

y = 100

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 407

x y log y

100 2

200 2.3

x y log y

2. Draw a semi-log graph of f by plotting the points (x, log y) from the table in

Question 1.

12345678910

3. Does the semi-log graph appear to be a line? If so, estimate the slope and the

y-intercept from the graph.

Slope: _______ y-intercept: _______

The marks on the “logarithmic

ruler” are the logarithms of the

numbers they represent.

10º

10¡

10™

10£

10¢

10∞

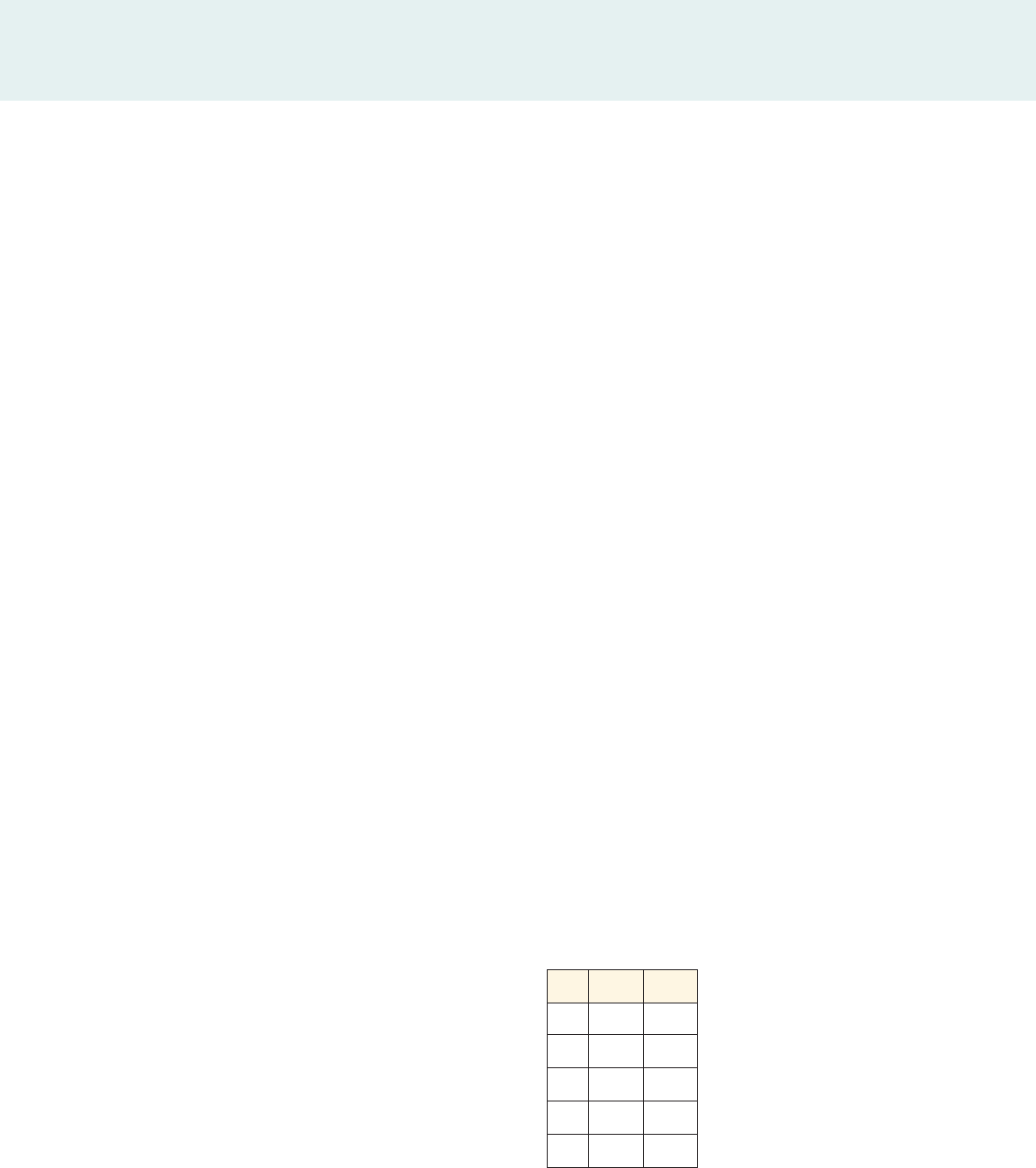
4. Let’s show that the graph in Question 2 is a line by finding an algebraic

formula for log y.

(a) Supply the missing reasons.

Definition of y

Take log of each side

______________

(b) The last equation in part (a) shows that log y is a linear function of x.

What is the slope? What is the y-intercept? Do your answers agree with

the line in the graph you sketched in Question 2?

III. Linearizing Data

A semi-log graph of an exponential function is a line. We can see this from

the following calculations:

Exponential function

Take the log of each side

Laws of Logarithms

To see that log y is a linear function of x, let , , and ;

then

So if we make a semi-log graph of exponential data, we would get a line with the fol-

lowing properties:

Slope: M ⫽ log a

y-intercept: B ⫽ log C

Let’s see how we can use this information to obtain a function that models expo-

nential data.

1. The following data are exponential. Note that the inputs are not equally

spaced.

Y = B + Mx

B = log CM = log aY = log y

log y = log C + x log a

log y = log Ca

y = Ca

log y L 2 + 0.3x

log y = log 100 + x log 2

log y = log1100

y = 100

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

408 CHAPTER 4

x y log y

0 10

0.5 20

2.0 160

3.0 640

4.5 5120

(a) Complete the log y column in the table.

(b) Make a semi-log graph of the data.

12345678910

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 409

2. Let’s find a function of the form that fits the data. (In other words, we

need to find a and C.)

(a) Estimate the slope and y-intercept from the graph.

Slope: M ⫽ _______

y-intercept: B ⫽ _______

(b) From the above we know that and . So

log a ⫽ _______

log C ⫽ _______

a ⫽ _______

C ⫽ _______

(d) So a function that fits the data is

(e) Check that the values of the function you found in part 2(d) agree with the

data.

y =

ⵧ

B = log CM = log a

y = Ca

The Even-Tempered Clavier

OBJECTIVE To learn how musical scales are related to exponential functions and how

exponential functions determine the pitch to which musical instruments are tuned.

Poets, writers, philosophers, and even politicians have extolled the virtues of music—

its beauty, its power to communicate emotion, and even its healing power. The philoso-

pher Nietzsche said that “without music life would be a mistake.” Perhaps that’s why

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

410 CHAPTER 4

Classical pianist Lang Lang

GABC CDEFGAB DE

One octave

FGABCDE

G# A# C# D# F# G# A# C# D# F# G# A# C# D#

some musicians—from rock stars to classical pianists—can command huge fees for

performing their art.

What is music, exactly? Is it just “noise” that happens to sound nice? In general,

music consists of tones played by instruments or sung by voices, either sequentially

(as a melody) or simultaneously (as a chord). Tones, the building blocks of music,

are sounds that have one dominant frequency.

The tones that we are familiar with from our everyday listening can all be re-

produced by the white and black keys of any properly tuned piano. The strings of a

piano produce specific sound frequencies; for instance, middle A has a fundamental

frequency of 440 cycles per second, or 440 Hertz (Hz). The other “A” keys on the pi-

ano are either higher-sounding, with frequencies of 880 Hz, 1760 Hz, and so on, or

lower-sounding, with frequencies of 220 Hz, 110 Hz, 55 Hz, and so on. To get from

one A to the next, you just need to double or halve the frequency. Every pair of notes

with the same letter name “sounds” the same to most listeners. Such notes are said

to be separated by “octaves” on the musical scale. In this Exploration we learn how

exponential functions allow us to create all the notes in the musical scale.

ROBERT VOS/AFP/Getty Images

I. Frequencies of Notes

We divide the interval between two notes that are an octave apart into 12 parts in such

a way that each note’s frequency is a fixed multiple of the preceding one. This fre-

quency interval is called a semitone in music theory. Since an octave involves mul-

tiplying the frequency by 2, each semitone therefore involves multiplying the fre-

quency by . This means that the frequencies are evenly spaced on a logarithmic

scale. The distance between semitones on a logarithmic scale is

So the keys on a piano are “evenly tempered” on a logarithmic scale.

1. The note immediately above middle A is A sharp (A# or B



), then the note

above A# is B, and so on. The frequency of each note is obtained by multi-

plying 440 (the frequency of middle A) by an appropriate power of . We

have

Complete the following table by calculating the frequencies of the notes pro-

duced by the keys in one octave on a piano, from middle A (known by piano

tuners as A4 or A440) to the next A (called A5).

440

1>12

L 493.883 Hz

440

1>12

L 466.164 Hz

440

1>12

= 440 Hz

1>12

log 2

1>12

log 2 L 0.025

1>12

2. The lowest-sounding key on a piano is an A (called A0 or Double Pedal A).

This key produces a note four octaves below middle A (A440).

(a) What fundamental frequency does the lowest piano key have?

(b) Many people lose the ability to hear low frequencies as they age. Elderly

people often can’t hear frequencies lower than 40 Hz. Will they be able to

hear the fundamental tone produced by the A0 key?

3. The highest A on the piano is A7, three octaves above middle A (A440). The

highest-sounding key of all on the piano is the 88th, called C8. Its frequency is

three semitones above A7.

(a) What is the frequency of A7?

(b) What is the frequency of C8, the highest key on the piano?

Can these people hear the sound of the highest key on the piano?

II. Intervals, Frequencies, and Dissonance

The “equally tempered” tuning of modern instruments described above did not come

into wide use until the late 17th century. Before that, musicians used many tunings

that sounded good to their ears and to their listeners’. Johann Sebastian Bach pub-

lished a set of preludes and fugues in 1722, called The Well-Tempered Clavier, which

was designed to popularize the new tuning system for keyboard instruments. Each

of the pieces in this work was written in one of the 24 major and minor keys in the

“well-tempered” tuning. Some listeners found the new tuning harsh and unmusical

for reasons that we now explore.

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 411

Key Frequency

440.000

A# B



466.164

C# D



D# E



F# G



G# A



1. When two or more keys on the piano are pressed simultaneously, the resulting

mixed sound is called a chord. When the ratios of the frequencies of the notes

in the chord involve small numbers, such as 2:1, 3:2, or 4:3, the chord sounds

pleasant and musical to most ears. But other ratios may sound unpleasant or

dissonant.

(a) A perfect fifth is an interval in a chord between two notes whose frequen-

cies are in the ratio 3/2. On the piano, this is approximated by two notes

that are seven semitones apart (for instance, C and G). Use your table

from Problem I.1 to determine the ratio between the frequencies of G and

C. How far does this differ from the ideal ratio of 3/2?

(b) A perfect fourth is an interval between two notes with frequencies in the

ratio 4/3. On the piano a fourth is approximated by two notes that are five

semitones apart (for instance, C and F). What is the ratio between the

frequencies of F and C on the piano? How far does this differ from the

ideal ratio of 4/3?

fourths might find the modern tuning of a piano to be dissonant?

2. In an octave the two notes have a frequency ratio of 2/1. So to divide an octave

into 12 semitones, the frequency of each note is times the frequency of

the preceding note:

(a) In a perfect fifth the two notes have a frequency ratio of 3/2. If we divide a

perfect fifth into seven semitones, explain why the frequency of each note is

times the frequency of the preceding note:

(b) In a perfect fourth the two notes have a frequency ratio of 4/3. To divide a

perfect fourth into five semitones, by what factor must the frequency of

each note be multiplied to get the frequency of the next note?

Explain why this means that we can’t tune a piano (with even tempering)

so that it has exact perfect fifths as well as exact perfect fourths.

frequency of note = a

ⵧ

* frequency of preceding note

frequency of note = A

1>7

* frequency of preceding note

13>22

1>7

frequency of note = A

1>12

* frequency of preceding note

1>12

412 CHAPTER 4

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

413

Secret connections? When a volleyball is hit, it goes flying through the air,

but it always comes back down. The function that describes how the volleyball

travels is a quadratic function—it’s the function that describes how gravity

pulls down on objects. Of course, this same function also determines how high

a rocket reaches or how your keys fall when they are dropped. But we’ll see in

this chapter that a quadratic function also models how long your car tires will

last (as a function of the tire pressure) or how much grain a farm produces (as

a function of the amount of rainfall). So what’s the connection between the

volleyball and crop yield? The connection is a secret that has been discovered

by using algebra. The volleyball goes up and then down, but so does crop

yield; the more rain, the more crop is produced—up to a point. If there is too

much rain, crop yield begins to decrease. That these very different processes

can be described by the same type of function is the secret to the usefulness of

algebra.

5.1 Working with Functions:

Shifting and Stretching

5.2 Quadratic Functions

and Their Graphs

5.3 Maxima and Minima: Getting

Information from a Model

5.4 Quadratic Equations: Getting

Information from a Model

5.5 Fitting Quadratic Curves

to Data

EXPLORATIONS

Transformation Stories

2 Torricelli’s Law

3 Quadratic Patterns

Quadratic Functions

and Models