Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

374 CHAPTER 4

■

Logarithmic Functions and Exponential Models

41–48

■ Use a graphing calculator to find all solutions of the equation.

41. 42.

43. 44.

45. 46.

47. 48.

49. Compound Interest Aviel invests $6000 in a high-yield uninsured certificate of

deposit that pays 4.5% interest per year, compounded quarterly.

(a) Find a formula for the amount A of the certificate after t years.

(b) What is the amount after 2 years?

50. Compound Interest Ping invests $4000 in a saving certificate that has an interest

rate of 2.75% per year, compounded semiannually.

(a) Find a formula for the amount A of the certificate after t years.

(b) What is the amount after 4 years?

51. Compound Interest Suzanne is planning to invest $2000 in a certificate of deposit.

How long does it take for the investment to grow to $3000 under the given conditions?

(a) The certificate of deposit pays interest annually, compounded every month.

(b) The certificate of deposit pays interest annually, compounded continuously.

52. Compound Interest Masako is planning to invest $5000 in a certificate of deposit.

How long does it take for the investment to grow to $8000 under the given conditions?

(a) The certificate of deposit pays 3.55% interest annually, compounded every month.

(b) The certificate of deposit pays 3.05% interest annually, compounded continuously.

53. Salmonella Bacteria Count Although cooking meat kills the microorganisms in it,

they may survive gentle frying and roasting, especially if the meat was not properly

defrosted before preparation. Inspectors for the U.S. Department of Agriculture test for

Salmonella in a sample of chicken at a meat-packing plant. The sample is found to have

a bacteria count of 15 colony-forming units per milliliter (CFU/mL). The sample is kept

at a temperature of , and 6 hours later the count is 20,000 CFU/mL.

(a) Find the instantaneous growth rate r for the bacteria count in the sample.

(b) Find an exponential model for the bacteria count in the sample, where t

is measured in hours.

(d) How long will it take for the bacteria count to reach 10 million CFU/mL?

(e) Find the doubling time for the Salmonella bacteria.

54. E. coli Bacteria Count Inspectors for the U.S. Department of Agriculture test a

sample of ground beef for the bacterium E. coli. The sample is found to have a bacteria

count of 100 colony-forming units per milliliter (CFU/mL). The sample is kept at a

temperature of , and 2 hours later the meat has a count of 13,300 CFU/mL.

(a) Find the instantaneous growth rate r (per hour) for the bacteria count in the sample.

(b) Find an exponential model for the bacteria count in the sample, where t

is measured in hours.

(d) How long will it take for the bacteria count to reach one million CFU/mL?

(e) Find the doubling time for the population of E. coli bacteria.

55. Population of Ethiopia In 2003 the United Nations estimated that the population of

Ethiopia was about 70.7 million, with an annual growth rate of 2.9%. Assume that this

rate of growth continues.

f 1t 2

= Ce

100°F

f 1t 2= Ce

80°F

- 2 = x

- x4

-x

= 1x

x = ln14 - x

- x = log1x + 12

-x

= x - 1e

=-x

log x = x

- 2ln x = 3 - x

CONTEXTS

SECTION 4.5

■

Exponential Equations: Getting Information from a Model 375

(a) Find the yearly growth factor a.

(b) Find an exponential growth model for the population t years since 2003.

(d) Use the model found in part (b) to predict the year in which the population will

reach 90 million.

56. Population of Germany In 2004 the population of Germany was about 82.5 million,

with an annual growth rate of 0.02%. Assume that this rate of growth continues.

(a) Find the yearly growth factor a.

(b) Find an exponential growth model for the population t years since 2004.

(d) Use the model found in part (b) to predict the year in which the population will

reach 83 million.

57. Pot of Chili Angela prepares a large pot of chili the night before a church potluck.

The temperature of the chili is , and it must cool down to before it can be

stored in the refrigerator. Assume that the ambient temperature is and the heat

transfer coefficient is .

(a) Find a model for the temperature T of the pot of chili t hours after cooling.

(b) How long will it take for the pot of chili to cool down to the desired temperature of

58. Time of Death Newton’s Law of Cooling is used in homicide investigations to

determine the time of death. Suppose that a body is discovered in a location whose

ambient temperature is . The police determine that the heat transfer coefficient in

this case is . (The heat transfer coefficient depends on many factors,

including the size of the body and the amount of clothing.) Normal body temperature is

(a) Find a model for the temperature T of the body t hours after death.

(b) When the body was found, it had a temperature of . Find the length of time the

victim has been dead.

59. Boiling Water A kettle of water is brought to a boil in a room where the temperature

is . After 15 minutes the temperature of the water has decreased from to

(a) Find the heat transfer coefficient k, and find a model for the temperature T of the

water t hours after it is brought to a boil.

(b) Use the model to predict the temperature of the water after 25 minutes. Illustrate by

graphing the temperature function.

(d) Graph the function T to confirm your answers to parts (b) and (c).

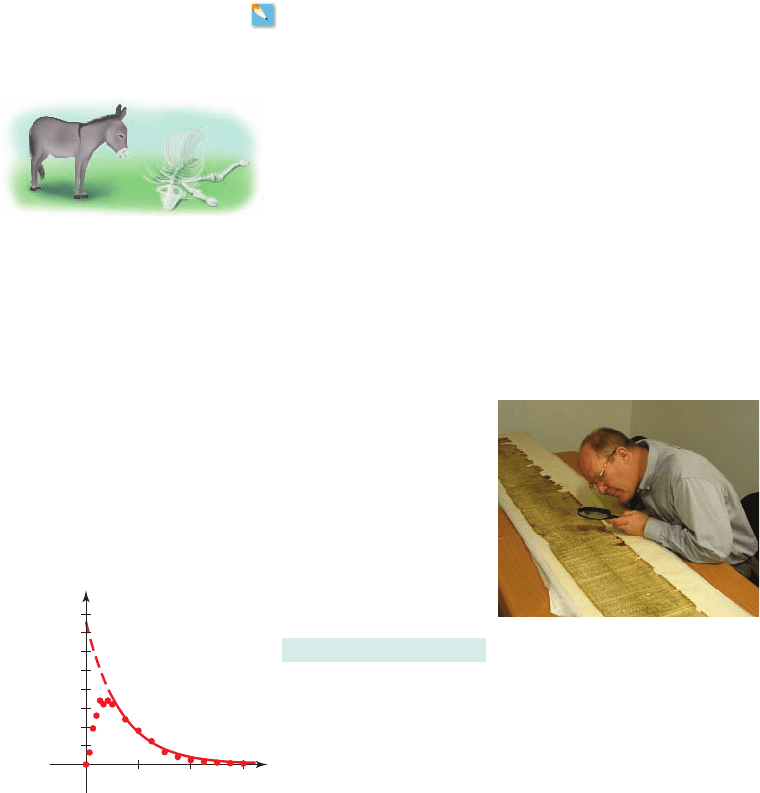
60. Cooling Turkey A roasted turkey is taken from an oven when its temperature has

reached and is placed on a table in a room where the temperature is . The

graph shows the temperature of the turkey after x hours.

(a) Find a model for the temperature T of the turkey t hours after it is taken out of the

oven.

(b)

Use the model to predict the temperature of the turkey after 45 minutes.

61. Radioactive Radium The half-life of radium-226 is 1600 years. Suppose we have a

22-mg sample.

(a) Find the yearly growth factor a.

(b) Find an exponential model for the mass remaining after t years.m1t 2= Ca

100°F

75°F185°F

40°C

75°C

100°C20°C

72°F

98.6°F

k = 0.1947

60°F

70°F

k = 2.895

65°F

70°F212°F

f 1t 2= Ca

100

150

185

(0.5, 150)

376 CHAPTER 4

■

Logarithmic Functions and Exponential Models

(d) After how long will only 18 mg of the sample remain?

62. Radioactive Cesium The half-life of cesium-137 is 30 years. Suppose we have a

10-gram sample.

(a) Find the yearly growth factor a.

(b) Find an exponential model for the mass remaining after t years.

(d) After how long will only 2 mg of the sample remain?

63. Plutonium-239 A nuclear power plant produces radioactive plutonium-239, which

has a half-life of 24,110 years. Because of its long half-life, plutonium-239 must be

disposed of safely. How long does it take 100 grams of radioactive waste from the

nuclear power plant to decay to 10 grams?

64. Strontium-90 One radioactive material that is produced in atomic bombs is the

isotope strontium-90, which has a half-life of 28 years. If a person is exposed to

strontium-90, it can collect in human bone tissue, where it can cause leukemia and other

cancers. If an atomic bomb test site is contaminated by strontium-90, how long will it

take for the radioactive material to decay to 10% of the original amount?

65. Carbon-14 Dating Archeologists find an ancient shard of pottery and use some burnt

olive pits found in the same layer of the site to determine the age of the shard. The

archeologists determine that the olive pits contain 69.32% of the carbon-14 that is present in

a living olive. (The half-life of carbon-14 is 5730 years.) How old is the shard of pottery?

66. Carbon-14 Dating A donkey bone is estimated to contain 73% of the carbon-14

that it contained originally. How old is the donkey bone? (The half-life of carbon-14

is 5730 years.)

67. Dead Sea Scrolls The Dead Sea Scrolls are documents that contain some of the

oldest known texts of parts of the Hebrew bible. They were discovered between 1947

and 1956 in several caves near the ruins of the ancient settlement of Khirbet Qumran on

the northwest shore of the Dead Sea. Archeologists determine that a sample taken from

the scrolls contains 79.10% of the carbon-14 that it originally contained. (The half-life

of carbon-14 is 5730 years.)

(a) Estimate the age of the Dead Sea Scrolls.

(b) Search the Internet for the historical date of the writing of the Dead Sea Scrolls.

How does this date compare with your estimate?

m1t 2= Ca

Donald Parry

0.3

0.4

0.2

0.1

y (mg/mL)

Time (h)

68. Algebra and Alcohol The table in the Prologue (page P2) gives the alcohol

concentration at different times following the consumption of 15 mL of alcohol. A

scatter plot of the data (see the margin) shows that the alcohol concentration reaches a

maximum in about half an hour and then begins to decay exponentially. The function

closely models the decay part of the alcohol concentration. Use this function to

determine the time at which the concentration decays to 0.05 mg/mL.

L1t 2= 0.38e

-1.5t

SECTION 4.6

■

Working with Functions: Composition and Inverse 377

4.6 Working with Functions: Composition and Inverse

■

Functions of Functions

■

Reversing the Rule of a Function

■

Which Functions Have Inverses?

■

Exponential and Logarithmic Functions as Inverse Functions

IN THIS SECTION… we study a method of combining functions called composition. We

also study inverse functions and see how the logarithm and exponential functions are

inverses of each other.

■ Functions of Functions

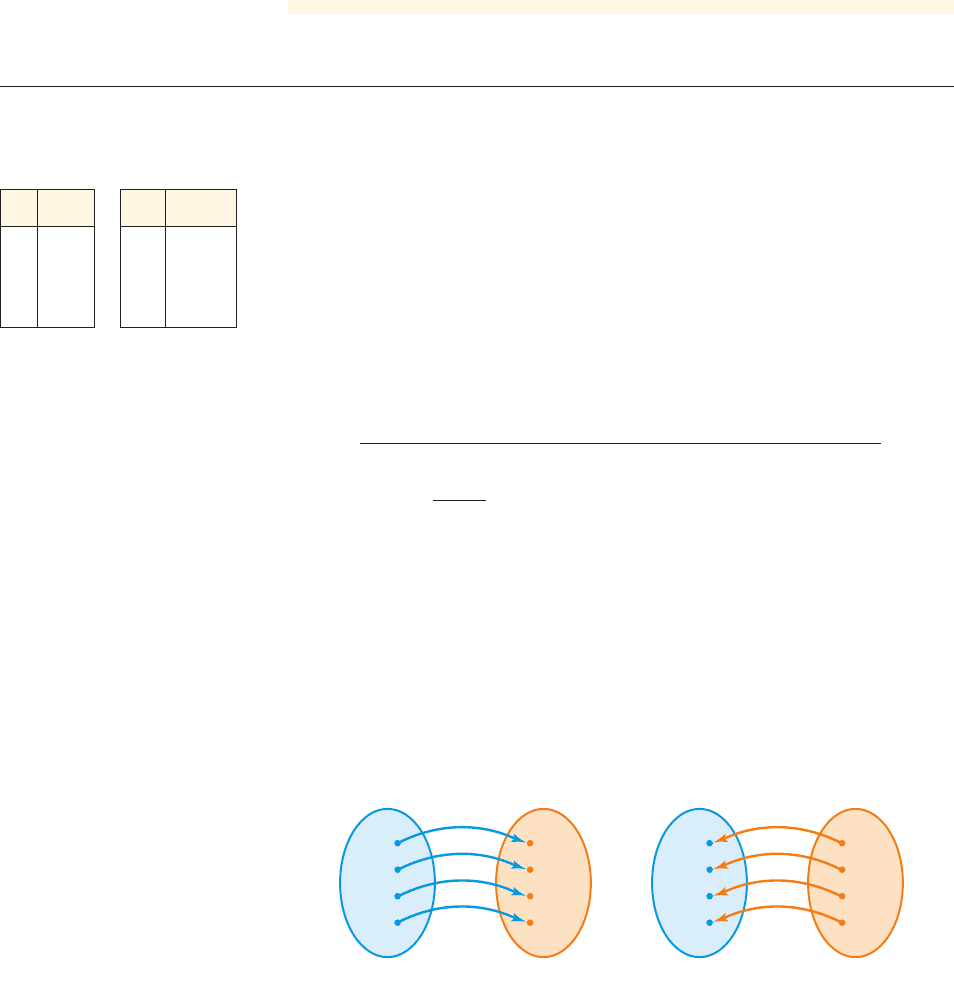
In many real-world situations we need to apply several functions in a row, that is, the

output of one function is used as the input to the next function. For example, suppose

you work for $8 an hour, and you pay tax at the rate of 5%. The function that gives

your pay for working x hours is , and the function that calculates the tax

on an income of x dollars is .T1x2= 0.05x

P1x 2= 8x

0 h

1 h

2 h

3 h

$16

$24

(dollars)

Work (hours)

$0.00

$0.40

$0.80

$1.20

Tax (dollars)

figure 1 From “hours worked” to “pay received”

to “tax paid”

table 1

P1x 2 T1P1x 22

0 0 0

1 8 0.40

2 16 0.80

3 24 1.20

4 32 1.60

5 40 2.00

6 48 2.40

7 56 2.80

Function In Words

P1x 2= 8x

“Pay for working x hours”

T1x 2= 0.05x

“Tax on x dollars”

Let’s say that we want to find how much tax you pay when you work x hours. To do

this, we must apply the functions P and T in the appropriate order. We start with the

input x hours, apply the function P to get the pay, and then apply the function T

to get the tax on that pay. For example, if you work 2 hours, then your pay is

dollars. Then we apply the function T to this output to get

. The diagram in Figure 1 shows how we apply these two

functions.

T116 2= 0.051162= 0.80

P12 2= 8122= 16

What we did was start with an input of x hours, apply the function P to get ,

then apply the function T to the result to get . We can express this as a single

function whose input x is the number of hours worked and whose output is the

tax owed. Several values of are given in Table 1. In general we call the

process of applying one function to the output of another composition of functions.

T1P1x 22

L1x 2

T1P1x 22

P1x 2

378 CHAPTER 4

■

Logarithmic Functions and Exponential Models

example

Composing Functions

Find the composition of the tax function with the pay function

Solution

We use L as the name of the new composite function. Then

Definition of the new function L

Definition of P

Definition of T

Simplify

So the new function is . You can check that this function gives the val-

ues in Table 1.

■ NOW TRY EXERCISE 15 ■

L1x 2= 0.40x

= 0.40x

= 0.0518x2

= T18x2

L1x 2= T1P1x 22

P1x 2= 8x

T1x 2= 0.05x

example

A Function of a Function

Let and . Give a verbal description of each of the following

composite functions, and then find an algebraic expression for the function.

(a)

(b)

Solution

(a) The function first applies the rule f and then applies the rule .

So M is the rule “Square, then add 1.” In symbols we have

Definition of the function M

Definition of f

Definition of g

(b) The function first applies the rule and then applies the rule f.

So N is the rule “Add 1, then square.” In symbols we have

g N1x 2= f 1g 1x 22

M1x 2= x

+ 1.

= x

+ 1

= g1x

M1x 2= g1f 1x 22

gM1x2= g1f 1x 22

N1x 2= f 1g1x 22

M1x 2= g1f 1x 22

g1x 2= x + 1f 1x2= x

Of course, to be able to compose f with , the range of must be contained in

the domain of f. In the next example we find an expression for the composition of

the “Tax” and “Pay” functions described above.

The Composition of Functions

Given two functions f and , we can make a new function h called the

composition of f with , defined by

h1x 2= f 1g1x 22

SECTION 4.6

■

Working with Functions: Composition and Inverse 379

■ Reversing the Rule of a Function

Definition of the function N

Definition of g

Definition of f

So .

■ NOW TRY EXERCISE 17 ■

N1x 2= 1x + 12

= 1x + 12

= f 1x + 12

N1x 2= f 1g1x 22

P1x 2

0 12

1 14

2 16

3 18

-1

1x 2

12 0

14 1

16 2

18 3

$12

$14

$16

$18

Price

Function P

Toppin

$12

$14

$16

$18

Price

Inverse function P

⫺1

Toppin

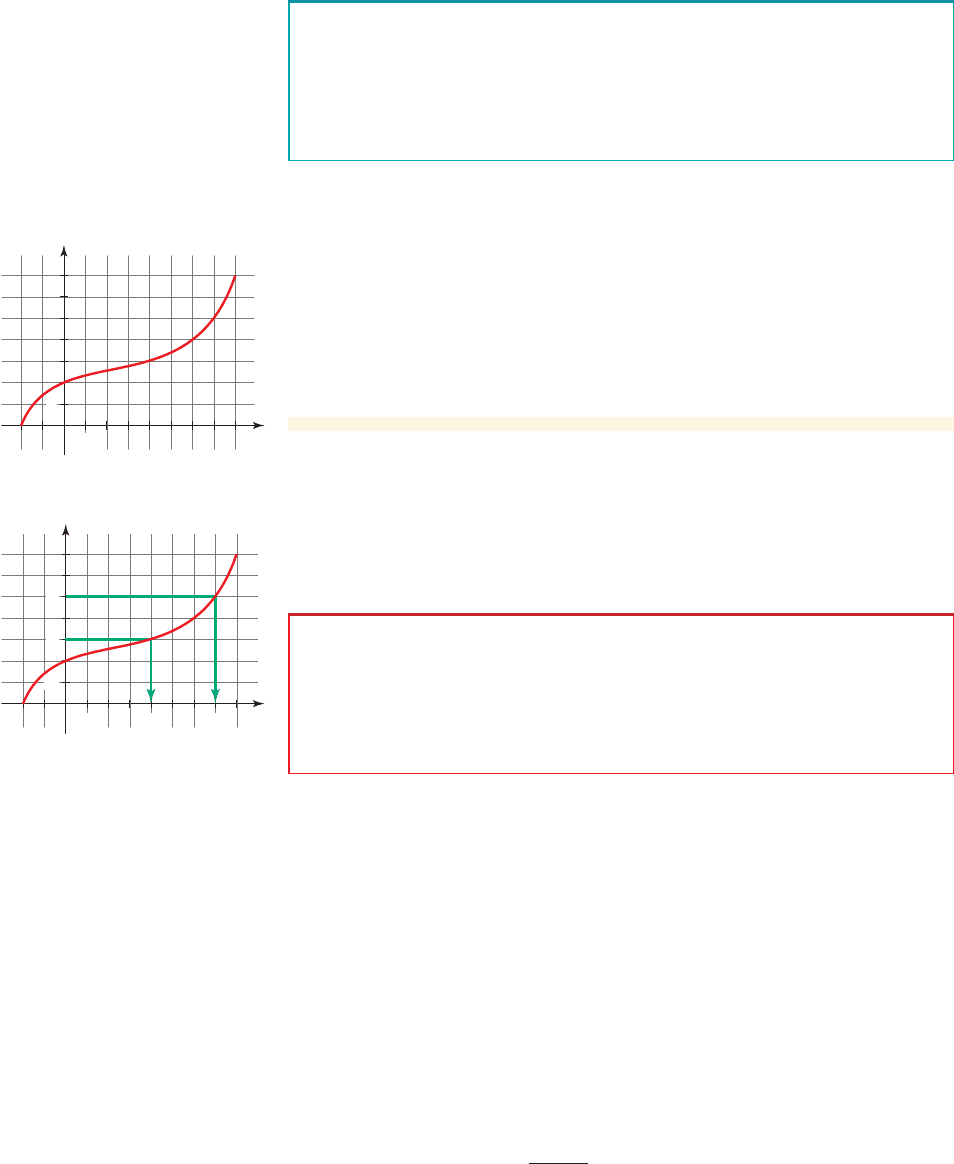
figure 2 The function “reverses” the function P.P

-1

Function In Words

P1x 2= 2x + 12

“Price of a pizza with x toppings”

-1

1x 2=

x - 12

“Number of toppings of a pizza with price x”

The rule P is “Multiply by 2, then add 12,” and the rule for is “Subtract 12,

then divide by 2.” Do you see how the rule reverses the rule for P? Try starting

with 5 toppings. Apply P to get 22, then apply to 22 to get back to 5.

P 51022

⫺1

51022

The diagrams in Figure 2 show the relationship between P and .P

-1

Multiply by 2

Divide by 2

Add 12

Subtract 12

In general, the inverse of a function is defined as follows.

We often need to reverse the rule of a function. In other words, we might want to find

the rule that takes us from the output of a function back to the corresponding input.

For example, suppose that at your local pizzeria the daily special is $12 for a

plain cheese pizza plus $2 for each additional topping. We can express the price of

the pizza as a function whose input x is the number of toppings and

whose output is the price. The function that “reverses” the rule of P is the function

whose input is the price and whose output is the number of toppings. You can check

that the rule for getting the number of toppings from the price is “Subtract 12 from

the price, then divide by 2.” This rule “reverses” the rule P; the notation for this

new rule is (read “P inverse”). So is the function . (The

tables in the margin give several values of P and .)P

-1

1x 2= 1x - 122>2P

-1

P1x 2= 2x + 12

380 CHAPTER 4

■

Logarithmic Functions and Exponential Models

example

Finding the Values of f

⫺1

Graphically

The graph of a function f is given in Figure 3. Use the graph to find the following.

(a) (b)

Solution

(a) From the graph we see that , so . (See Figure 4.)

(b) From the graph we see that , so . (See Figure 4.)

■ NOW TRY EXERCISE 35 ■

Let’s see how we can find an equation for the inverse of a function f. From the def-

inition we see that if we can solve the equation for x, then we must have

. If we then interchange x and y, we get , which is the function

we want. Thus, we have the following procedure for finding the inverse of a function.

How to Find the Inverse of a Function

y = f

-1

1x 2x = f

-1

1y2

y = f 1x2

-1

15 2= 7f 17 2= 5

-1

132= 4f 142= 3

-1

152f

-1

13 2

figure 3 Graph of f

1 4 7

figure 4 Finding values of

from the graph of f

-1

In the next example we use these steps to find the inverse of the pizza function

P described earlier in this section.

To find the inverse of a function f:

Step 1 Write the function in equation form: .

Step 2 Solve this equation for x in terms of y (if possible).

Step 3 Interchange x and y. The resulting equation is .y = f

-1

1x 2

y = f 1x 2

Expressing a function in equation

form is studied in Section 1.5.

example

Finding the Inverse of a Function

Find the inverse of the function .

Solution

First we write P in equation form:

Then we solve this equation for x:

Equation

Subtract 12

Divide by 2 and switch sides

x =

y - 12

y - 12 = 2x

y = 2x + 12

P1x 2= 2x + 12

If a function f has domain A and range B then its inverse function (if it

exists) is the function with domain B and range A defined by

for any y in B.

-1

1y 2= xif and only iff 1x2= y

-1

The Inverse of a Function

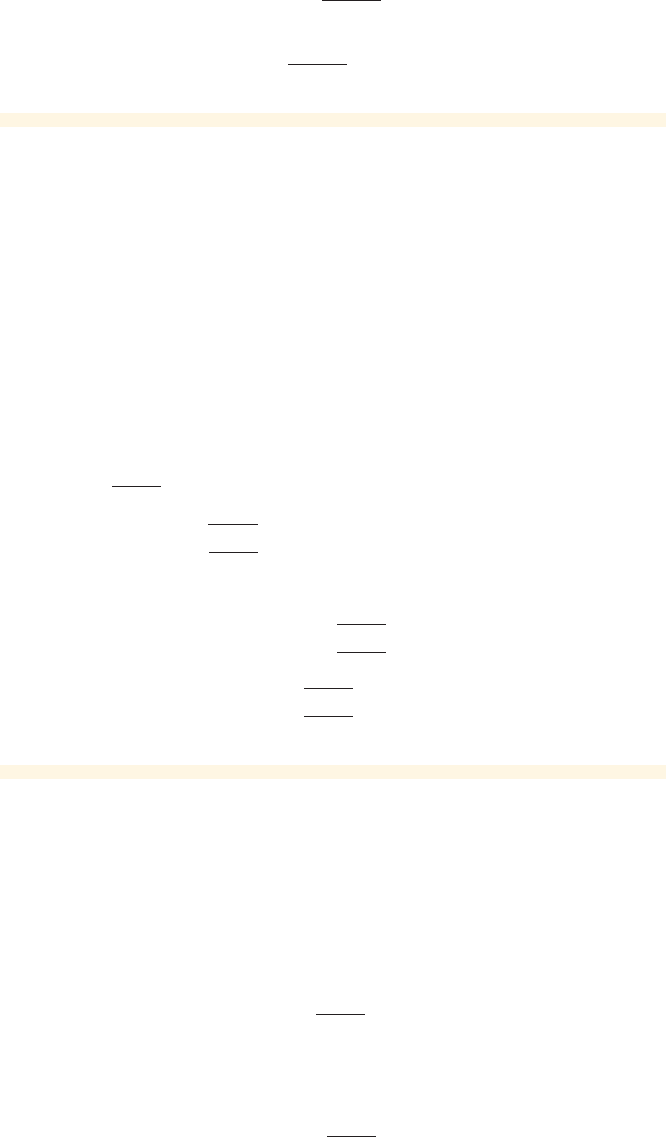
SECTION 4.6

■

Working with Functions: Composition and Inverse 381

In Example 4, notice how the rule

reverses the rule P: The func-

tion P is the rule “Multiply by 2,

then add 12.” The function is the

rule “Subtract 12, then divide by 2.”

-1

example

Finding the Inverse of a Function

Find the inverse of the function .

Solution

First we write f in equation form:

Then we solve this equation for x:

Equation

Subtract 1

Divide by 2

Take the cube root and switch sides

Finally, we interchange x and y:

So the inverse function is .

■ NOW TRY EXERCISE 61 ■

It is not always possible to give a simple verbal description of the inverse of a

function. The next example shows why.

-1

1x2=

x - 1

y =

x - 1

x =

y - 1

= x

y - 1 = 2x

y = 2x

+ 1

y = 2x

+ 1

f 1x2= 2x

+ 1

In Example 5, notice how the rule

reverses the rule f : The function

f is the rule “Cube x, multiply by 2,

then add 1.” The function is the

rule “Subtract 1, divide by 2, then

take the cube root.”

-1

Finally, we interchange x and y:

So the inverse function is .

■ NOW TRY EXERCISE 57 ■

-1

1x 2=

x - 12

y =

x - 12

example

Finding the Inverse of a Function

Find the inverse of the function .

Solution

First we write f in equation form:

y =

x + 2

f 1x2=

x + 2

382 CHAPTER 4

■

Logarithmic Functions and Exponential Models

Let f be a function with domain A and range B. The function is the inverse

of f if and only if the following properties are satisfied:

for every x in A

for every x in B f 1g1x 22= x

g1f 1x 22= x

We can now use these properties to check whether two functions are inverses of

each other.

example

Checking That f and g Are Inverses of Each Other

Show that and are inverses of each other.

Solution

We need to check that and . We have

Definition of g

Definition of f

Simplify

Cancel 5

= x

15x + 2 2- 2

f 1g1x 22= f 15x + 2 2

g1f 1x22= xf 1g1x22= x

g1x 2= 5x + 2f 1x 2=

x - 2

Then we solve this equation for x.

Equation

Multiply by

Distributive Property

Bring the x-terms to one side

Factor x

Divide by and switch sides

Finally, we interchange x and y:

So the inverse function is .

■ NOW TRY EXERCISE 63 ■

How can we check whether our answers to the preceding two examples are cor-

rect? By definition the inverse undoes what f does: If we start with x, apply f, and

then apply , we arrive back at x, where we started. Similarly, f undoes what

does. We can express these facts as follows.

Inverse Function Properties

-1

1x2=

3 - x

y =

3 - x

3 - y x =

3 - y

2 y = x13 - y2

2 y = 3x - yx

yx + 2y = 3x

x + 2 y1x + 22= 3x

y =

x + 2

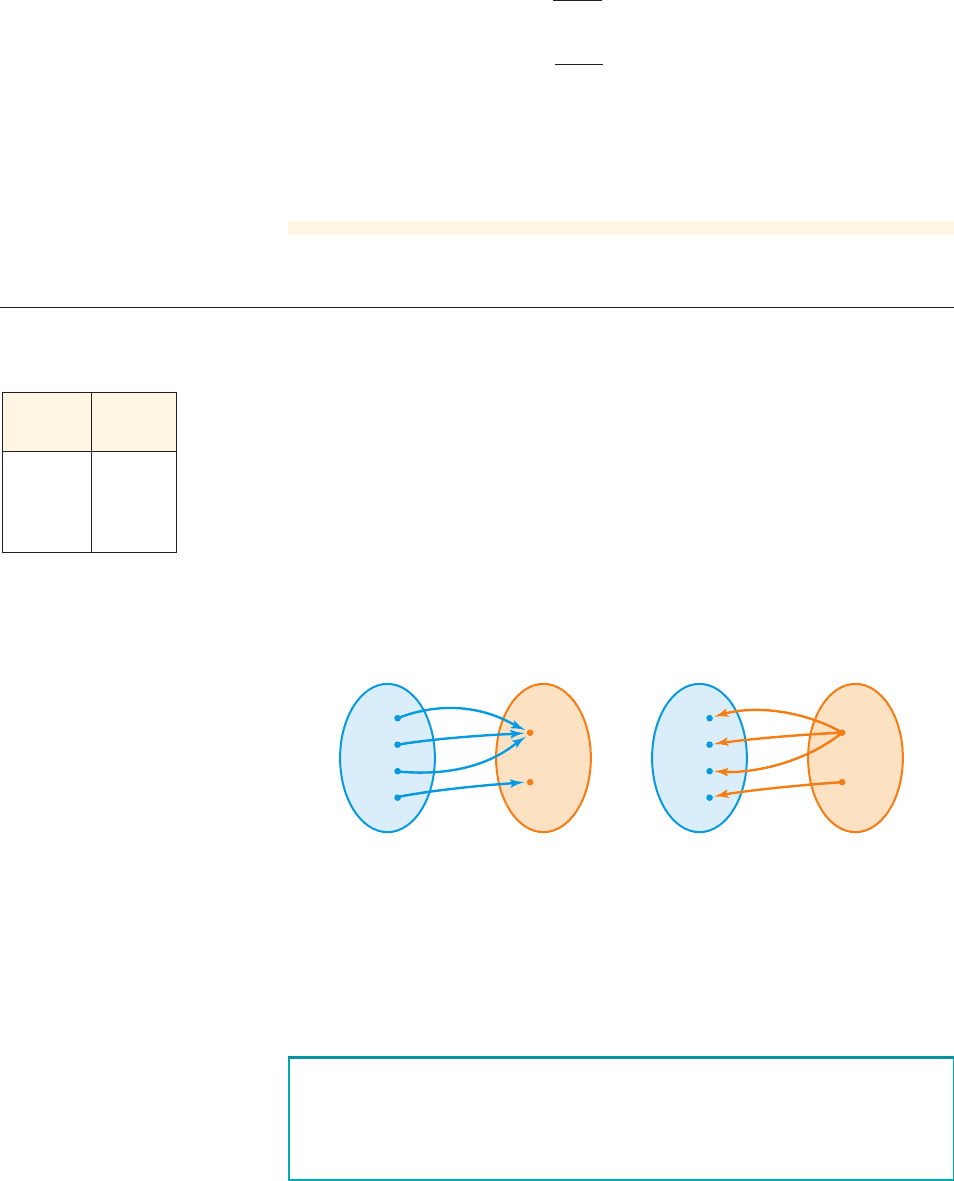
SECTION 4.6

■

Working with Functions: Composition and Inverse 383

■ Which Functions Have Inverses?

It’s not always possible to find the inverse of a function. For example, suppose your

local pizzeria has a coupon that gives you “up to two toppings for the same $12 price

as the plain cheese pizza—and $2 for each additional topping after that.” Table 2 gives

the price of a pizza for different numbers of toppings (if you use the coupon). So we

have a function P whose input is the number of toppings and whose output is the price.

If Jason tells you that he paid $12 for a pizza, you can’t tell how many toppings

the pizza had. Jason could have chosen to get one free topping, two free toppings, or

no free topping. The problem in finding an inverse of this function is that one output

corresponds to two (or more) different inputs. The diagram in Figure 5 illustrates the

situation. When we reverse the arrows, we get a relation that is not a function. So

there is no inverse function for this function.

table

Input:

toppings

Output:

price

0 12

1 12

2 12

3 14

Also

Definition of f

Definition of g

Cancel 5

Simplify

This shows that f and are inverses of each other.

■ NOW TRY EXERCISE 37 ■

= x

= 1x - 22+ 2

= 5 a

x - 2

b+ 2

g1f 1x22= ga

x - 2

$12

$14

Price

Function

Toppings

$12

$14

Price

Not a function

Toppings

figure 5

For a function to have an inverse, different inputs must correspond to different

outputs. (We can’t have two different inputs giving the same output.) Functions with

this property are called one-to-one, as in the following definition.

Definition of One-to-One Function

A function f is called one-to-one if no two different inputs have the same

output; that is,

x

⫽ x

thenf 1x

2⫽ f 1x